虚時間発展について

はじめに

量子力学や量子計算において虚時間発展 (imaginary time evolution) という言葉がしばしば登場する. しかし, 筆者はあまり詳しくは知らなかった. そのため今回少しまとめた.

虚時間発展について簡単に述べると, Hamiltonian $H$ の Schrödinger 方程式

$$-i\frac{d\psi}{dt}=H\psi, \qquad t\geq 0 \tag{1}$$

から虚数単位 $i$ を消した方程式

$$-\frac{d\psi}{dt}=H\psi, \qquad t\geq 0 \tag{2}$$

を考えるというものである. (1) によって定まる半群 (ユニタリー群) $(e^{itH})_{t\geq 0}$ において, 形式上 $t\leftarrow it$ (虚数時間を代入) とすることで (2) によって定まる半群 $(e^{-tH})_{t\geq 0}$ が得られるため, 通常の量子系の時間発展 (1) と対比してタイトルのように虚時間発展と呼ばれるようである. そして次節以降で示すように, (2) による時間発展によって $H$ の基底状態を得られる確率を高めることができる, というのが虚時間発展法と呼ばれるものである.

準備

量子力学の舞台は Hilbert 空間であり, その上の自己共役作用素が重要な役割を果たす. 以下, $\mathcal{X}$ を複素可分 Hilbert 空間とし, 内積を $\langle\cdot,\cdot\rangle$ で表す. ただし, 量子力学の慣例に倣い, この内積は右線型, 左反線型とする. また, $x\in\mathcal{X}$ に対し, ノルム $\|x\|=\sqrt{\langle x,x\rangle}$ とする.

$H$ を $\mathcal{X}$ 上の自己共役作用素とする. このとき, $H$ のスペクトル分解を

$$H = \int \lambda \,dE(\lambda)$$

で表す. ここで, $(E(\lambda))_{\lambda\in\mathbb{R}}$ は $H$ のスペクトル族である.

虚時間発展

$\lambda_0=\inf_{\|\psi\|=1}\langle \psi,H\psi\rangle>-\infty$ とする. $\psi_0\in\mathcal{D}(H)$, $\|\psi_0\|=1$ に対し, 方程式 (2)

$$\begin{align*} \begin{cases} \displaystyle -\frac{d\psi}{dt} = H\psi, & t>0, \\[1em] \psi(0) = \psi_0 \end{cases} \end{align*}$$

の解は, 半群 $(e^{-tH})_{t\geq 0}$ を用いて, $\psi(t)=e^{-tH}\psi_0$ である. ただし, $t>0$ のとき $e^{-tH}$ はユニタリーではないため, $\psi(t)$ は必ずしも量子状態ではない, すなわち, $\|\psi(t)\|^2=\int e^{-2t\lambda}\,d\langle \psi_0,E(\lambda)\psi_0\rangle =1$ が常に成り立つわけではないことに注意する.
今, 有界可測関数 $f\colon\mathbb{R}\to\mathbb{R}$ に対し, $\|E(\lambda_0)\psi_0\|>0$ ならば,

$$\begin{align*} & \left| \int f(\lambda)\, \frac{d\langle \psi(t),E(\lambda)\psi(t)\rangle}{\|\psi(t)\|^2} - f(\lambda_0) \right| \\[1.5em] & \hspace{3em} \leq \frac{1}{\|E(\lambda_0)\psi_0\|^2} \int |f(\lambda)-f(\lambda_0)|\,e^{-2t(\lambda-\lambda_0)}d\langle\psi_0,E(\lambda)\psi_0 \rangle \\[1.5em] & \hspace{3em} \leq \frac{\sup_{\lambda\in\mathbb{R}}|f(\lambda)-f(\lambda_0)|}{\|E(\lambda_0)\psi_0\|^2} \int_{(\lambda_0,\infty)} \,e^{-2t(\lambda-\lambda_0)}d\langle\psi_0,E(\lambda)\psi_0 \rangle \tag{3} \end{align*}$$

である. したがって, 有界収束定理より,

$$\begin{align*} \int f(\lambda)\frac{d\langle \psi(t),E(\lambda)\psi(t)\rangle}{\|\psi(t)\|^2} \to f(\lambda_0), \qquad t\to\infty \end{align*}$$

である. よって, 次を得る.

定理 (虚時間発展法). 上で定めた $\lambda_0$ が $H$ の固有値であり, かつ初期状態 $\psi_0$ が $\lambda_0$ に対応する固有空間と直交しないとする. このとき, 時間発展 (2) により得られる量子状態 $\psi(t)/\|\psi(t)\|$ の $H$ による観測値の分布 $d\langle \psi(t),E(\cdot)\psi(t)\rangle/\|\psi(t)\|^2$ は, $t\to\infty$ で $\lambda_0$ に集中する Dirac 測度 $\delta_{\lambda_0}$ に弱収束する. このとき, $A\subset\mathbb{R}$ に対し,

$$\begin{align*} \lim_{t\to\infty}\int_A \frac{d\langle \psi(t),E(\lambda)\psi(t)\rangle}{\|\psi(t)\|^2} &= \begin{cases} 1, & \lambda_0\in A, \\ 0, & \lambda_0\notin A \end{cases} \end{align*}$$

が成り立つ. 特に, $\lambda_0$ が $H$ のスペクトル $\sigma(H)$ の孤立点ならば, $\delta=\inf_{\lambda\in\sigma(H)\setminus \{\lambda_0\}}|\lambda_0-\lambda|$ に対して,

$$\begin{align*} 1 - \frac{\|E(\lambda_0)\psi(t)\|^2}{\|\psi(t)\|^2} & \leq \frac{e^{-2t\delta}}{\|E(\lambda_0)\psi_0\|^2} \tag{4} \end{align*}$$

が成り立つ.

証明. $A\subset \mathbb{R}$, $f=\boldsymbol{1}_A$ に対して (3) を適用する. ここで $\boldsymbol{1}_A$ は定義関数である. (3) より,

$$\begin{align*} & \left| \int_A \frac{d\langle \psi(t),E(\lambda)\psi(t)\rangle}{\|\psi(t)\|^2} - \boldsymbol{1}_A(\lambda_0) \right| \\[1.5em] & \hspace{3em} \leq \frac{1}{\|E(\lambda_0)\psi_0\|^2} \int_{(\lambda_0,\infty)} e^{-2t(\lambda-\lambda_0)}d\langle\psi_0,E(\lambda)\psi_0 \rangle \end{align*}$$

が成り立つ. この不等式に対し, $t\to\infty$ および $A=\{\lambda_0\}$ とすれば求める主張がそれぞれ得られる. □

この定理は, 量子状態として十分大きな $t$ まで虚時間発展を行うことで, 高い確率 (fidelity) $\approx 1$ で $H$ の基底状態が得られることを意味している.

数値例

ここでは Dirichlet 境界条件の付いた1次元 Laplacian (2階微分作用素 $\partial^2_x:=\frac{d^2}{d x^2}$) を見てみる.
　開区間 $I=(0,1)$ とし, $L^2(I)$ 上の作用素 $-\partial^2_x$, $D(-\partial^2_x)=H^2(I)\cap H_0^1(I)$ とする. ここで, $H^2(I)$, $H_0^1(I)$ は Sobolev 空間である. $-\partial^2_x$ は $L^2(I)$ 上の自己共役作用素であり, スペクトルは固有値のみ, $\sigma(-\partial^2_x)=\sigma_p(-\partial^2_x)=\{n^2\pi^2\mid n=1,2,\dots\}$ である. 各固有値 $n^2\pi^2$ に対応する固有関数は, $\phi_n(x)=\sqrt{2}\sin n\pi x~(x\in I)$ である. このとき関数系 $(\phi_n)_{n=1,2,\dots}$ は $L^2(I)$ の正規直交系をなす.
　虚時間発展 (2) は, Dirichlet 境界条件を持つ1次元熱方程式

$$\begin{align*} \begin{cases} \displaystyle \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}, & t>0, ~x\in I, \\[1em] u(t,0) = u(t,1) = 0, & t\geq 0, \\[1em] u(0,x) = u_0(x), & x\in I \end{cases} \end{align*}$$

に対応する.
　初期条件 $u_0$ を次で定める:

$$\begin{align*} u_0(x)= \begin{cases} \sqrt{3}, & \displaystyle\frac{1}{6}\leq x\leq \frac{1}{2}, \\[1em] 0, & \textrm{otherwise.} \end{cases} \end{align*}$$

これに対して, 有限差分法を用いて数値解 $u(t,x)~(t\geq 0,\,x\in I)$ を計算し, 固有関数の近似が得られるか確認する.

$\phi_1$ (基底状態) の計算

今回我々は解析的に得られる固有関数系を知っているので, これを使って定理の通りの収束が見られるかどうかを確認する. その結果が図1である. 図中の fidelity は式 (4) 中の

$$\begin{align*} \frac{\|E(\lambda_0)\psi(t)\|^2}{\|\psi(t)\|^2} \end{align*}$$

に対応し, 今の場合

$$\begin{align*} \frac{|\langle u(t,\cdot),\phi_1 \rangle|^2}{\|u(t,\cdot)\|^2} &= \frac{|\int_0^1 u(t,x)\phi_1(x)dx |^2}{\int_0^1 |u(t,x)|^2dx} \end{align*}$$

である.
　虚時間発展により $t$ が十分大きいとき, 正規化された解

$$\begin{align*} \frac{u(t,\cdot)}{\|u(t,\cdot)\|} \end{align*}$$

が $\phi_1$ を近似する様子が確認できる.

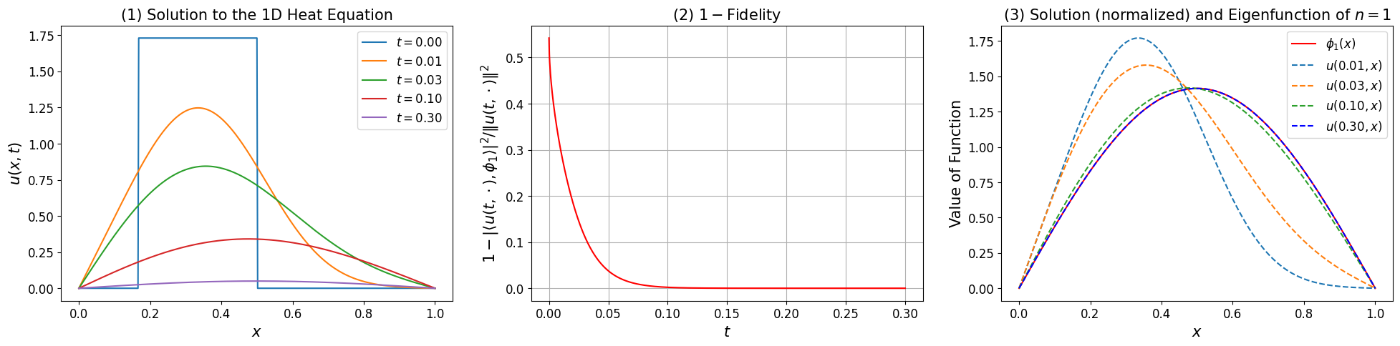
図1. 固有関数 $\phi_1$ への収束

$\phi_2,\phi_3,\dots$ (励起状態) の計算

今回の例や有限次元の場合のように, 集積点を持たない離散的な固有値同士の間に他のスペクトルが存在しない場合, 虚時間発展法の証明の考え方より, 初期条件をそれまでに得られた固有関数の成分を差し引いた初期条件, すなわち, 順に $\{\phi_1\},\{\phi_1,\phi_2\},\dots$ が得られたとき,

$$\begin{align*} & \frac{u_0 - \langle u_0,\phi_1 \rangle \phi_1}{\|u_0 - \langle u_0,\phi_1 \rangle \phi_1\|},~ \frac{u_0 - \langle u_0,\phi_1 \rangle \phi_1 - \langle u_0,\phi_2 \rangle \phi_2}{\|u_0 - \langle u_0,\phi_1 \rangle \phi_1 - \langle u_0,\phi_2 \rangle \phi_2\|},\dots \end{align*}$$

とすることで固有関数 $\phi_2,\phi_3,\dots$ を順に算出することができる. $\phi_2,\phi_3$ でそれを示したのが図2,3である. ただし, fidelity を通じた量子状態としての近似であるため, 符号反転 (位相のずれ) が生ずる場合は補正した.

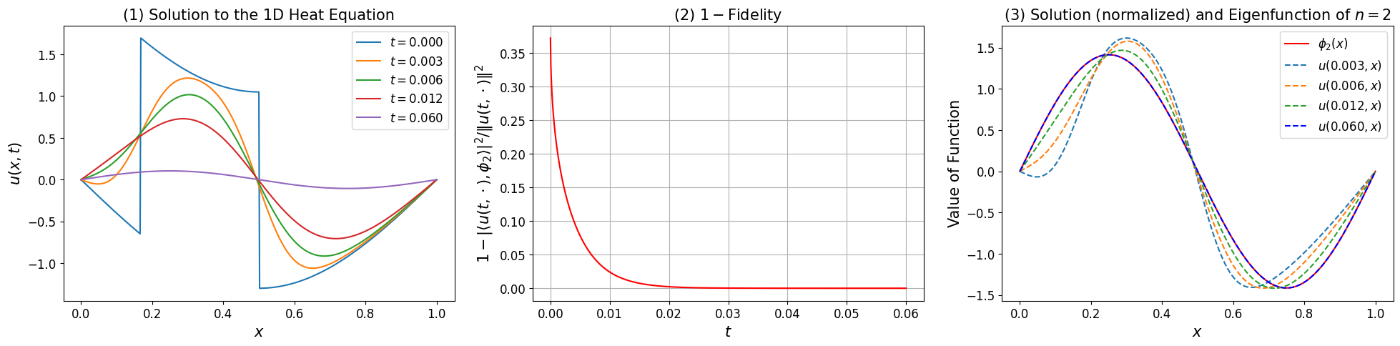
図2. 固有関数 $\phi_2$ への収束

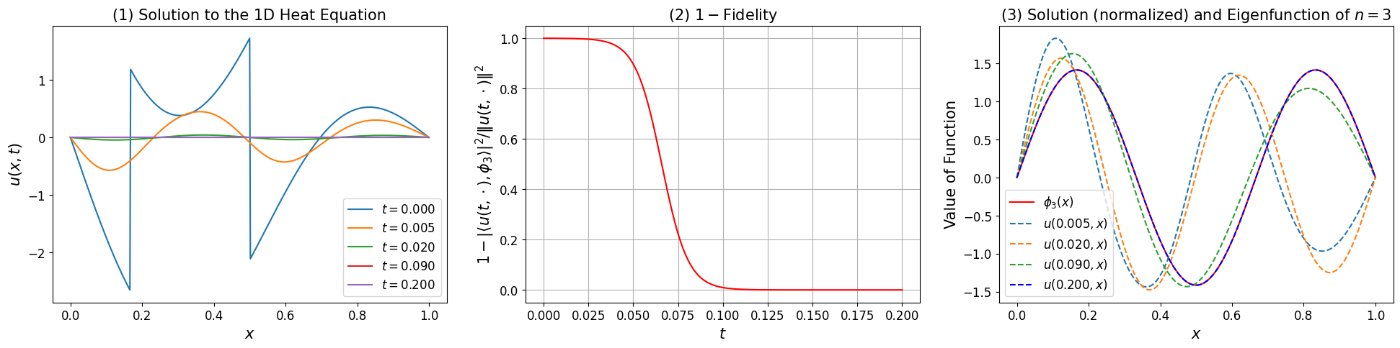
図3. 固有関数 $\phi_3$ への収束

解析的には

上記では解析的に解が得られるこの問題を取り扱い, 実際を想定し数値計算を行った. すでに述べた事実により Dirichlet 条件を付した作用素 $-\partial^2_x$ は次のようにスペクトル分解 (固有値分解) される:

$$\begin{align*} -\partial^2_x u_0 &= \sum_{n=1}^\infty n^2\pi^2 \langle \phi_n,u_0 \rangle \phi_n, \qquad u_0\in L^2(I)~\textrm{s.t.}~\sum_{n=1}^\infty n^4\pi^4|\langle \phi_n,u_0 \rangle|^2<\infty. \end{align*}$$

よって, $(e^{t\partial^2_x})_{t\geq 0}$ は

$$\begin{align*} e^{t\partial^2_x}u_0 &= \sum_{n=1}^\infty e^{-n^2\pi^2t} \langle \phi_n,u_0 \rangle \phi_n, \qquad u_0\in L^2(I) \end{align*}$$

である. これは虚時間発展の具体的な例であり, このことからも数値的に確認したことが成り立つことが確認できる.

量子コンピュータと虚時間発展

量子コンピュータ上ではユニタリーな演算しか行うことができない. そのため, 虚時間発展を行うことはできない. ただし, 工夫により虚時間発展を行う方法が知られている.

• arXiv:1804.03023: 変分法的な虚時間発展法. Ansatz を定めて, パラメータ更新を行っていくことで虚時間発展を行う.
• arXiv:2308.03605: 量子振幅増幅と確率的な虚時間発展の組合せにより, 量子状態の準備が古典に比べて2次の高速化して行えることを示した. その中で確率的虚時間発展として説明されている.

参考

1. 量子モンテカルロ法とは
2. qubitによる波動関数の虚時間発展のシミュレーション: a review
3. 新井朝雄, 「ヒルベルト空間と量子力学」, 共立講座 21世紀の数学 16, 2014, 共立出版.
4. 黒田成俊, 「関数解析」, 共立数学講座 15, 1980, 共立出版.
5. Heat Equation