😺

LoRA の論文紹介

2023/08/13に公開

NLP

LLM

tech

はじめに

本記事はとある勉強会で使用したものです。
10 分程度の発表を想定していますので、詳細については触れません。
対象の論文は以下となります。

LoRA とはなにか

LoRA とは Low-Rank Adaptation の略称です。その名のとおり Adapter の一種と考えることができますが、 Low-Rank が意味するところは次式で端的に表されます。

\tag{1} h = W_0x + \Delta Wx = W_0x + BAx

ここで $h$ は出力値、 $x$ は入力値、 $W_0 \in \mathbb{R}^{d \times k}$ は事前学習時の重み、 $\Delta W \in \mathbb{R}^{d \times k}$ は更新時に付加される重みです。数式から明らかなように $\Delta W = BA$ で、 $B \in \mathbb{R}^{d \times r}$ 、 $A \in \mathbb{R}^{r \times k}$ 、 $\mathrm{rank} \: r \ll \min \: (d, k)$ となるように $B$ と $A$ を指定します。なお、このとき $A = \mathcal{N} (0, \sigma ^2)$ 、 $B = 0$ で初期化します。

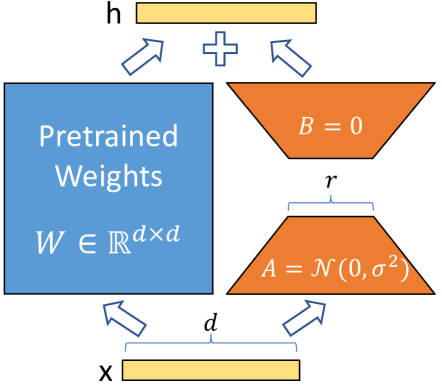
これを模式的に表したものが下図となります（計算にあたっては $W \in \mathbb{R}^{d \times d}$ としたようで、図でもそのように表現されています）。この $r$ というのが Low-Rank というわけです。今回は図の青色部分（ $W$ ）をベースモデル、オレンジ色部分（ $A$ と $B$ ）を LoRA 層と呼ぶことにします。

LoRA の模式図

LoRA にはどんな特徴があるか

本論文では LoRA の優れている点が 4 つ挙げられています。

ベースモデルを固定し、 LoRA 層を可変とすることで、タスクの切り替えが容易にできる。
低次元である LoRA 層のみが最適化の対象となるため、より効率的に計算することができる。
LoRA 層は線形写像であるから、ベースモデルにマージすることができる。
Prefix-Turning のような既存の様々な手法と組み合わせて使用することができる。

たとえば 2 について、 $r = 4$ として GPT-3 175B で実行したところ、 Full Fine-Tuning と比較して、 VRAM（GPU メモリ）の使用量は 1.2TB から 350GB に、チェックポイントにおける容量は 350GB から 35MB に、処理速度は 25% 高速になりました。

LoRA の性能はどうか

他の手法との性能を比較したものが以下 3 つのテーブルとなります。特に Fine-Tuning (FT) と比べると、他の Adapter と同様、パラメータの数を大幅に抑えることができています。また、多くのタスクで LoRA がより高い性能を示しています。

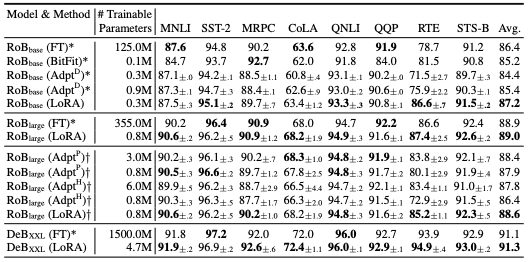
RoBERTa base/large と DeBERTa XXL における性能

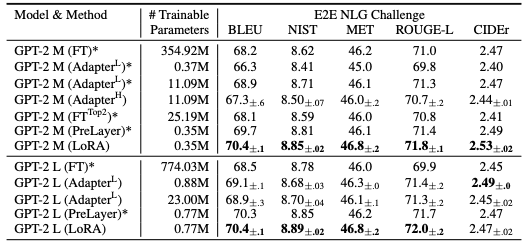
GPT-2 medium/large における性能

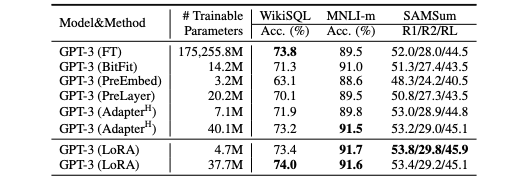
GPT-3 175B における性能

さらに GPT-3 175B における精度とパラメータ数との関係を見てみると、 LoRA が比較的安定した性能を発揮していることもわかります。

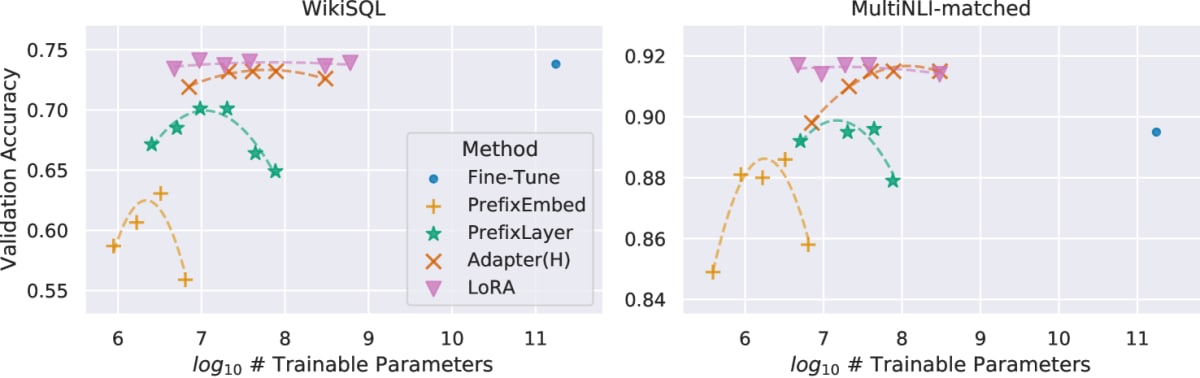
精度とパラメータ数

LoRA 層でなにが起きているのか

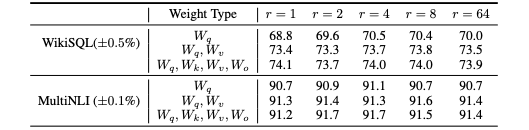
ここで、 $W, \: \Delta W, \: r$ の関係性を見てみましょう。最適化する層（ $W_q, \: W_k, \: W_v, \: W_o$ は query/key/value/output それぞれの注意機構の重み）が多いほど性能は上がりますが、次元については $r = 2$ のように小さくても十分な効果が期待できそうです。

最適化する層やランクによる性能の違い

$W$ を $\Delta W$ の部分空間に射影して、 Frobenius norm を求めます。ここから推察されるのは、Random と比較して $\Delta W$ は $W$ と強い相関を持っており、 $W$ に内在している特徴量を増幅しているということです。言い換えると、ベースモデルにある知識を LoRA 層が強調していることを示唆しています。

GPT-3 48 層目における Frobenius norm

おわりに

これまで見てきたとおり、 LoRA の原理自体は非常にシンプルです。線形変換をしているだけなのにも関わらず、場合によっては Fine-Tuning よりも高い性能が出るというのも非常に興味深い点かと思います。 LoRA 層（の線形性）が知識を強調する、という解釈が妥当かどうかはもう少し検証が必要なようにも感じましたが、これにより物事の抽象度が判別できるようになるのだとしたら、知識の習得過程についてもおもしろい議論ができるかもしれません。

今回は LLM の論文をちゃんと読むのは初めてだったということもあり、前提知識を整理するのにとても時間がかかってしまいました。はじめに「詳細については触れません」と書きましたが、「詳細については説明できません」というのが正直なところなので、注意機構や Transformer についての理解もこれから深めてゆければと考えています。