【物理】振り子の周期の厳密解の導出とpythonプログラム

はじめに

今回はいつもとは少し違う観点から記事を書いてみたいと思う。
いきなりだが、皆さんは振り子の周期の話を聞いたことはあるだろうか？一般的に高校では振り子の周期は、振幅に依存しないと習う。つまり、どれだけ揺れさせても周期は変わらないと教わる。
振り子だとイメージが湧きづらいと思うので、ブランコを想像してみよう。

高い位置から漕ぐのをやめた人と、低い位置から漕ぐの」をやめた人を比べたときに、周期が変わらないというのが高校で教わった振り子の式である。では、本当にそうなのだろうか？もちろん現実世界では空気抵抗やその他の摩擦が考えられるため、放置していればいつかは振り子は止まる。では、空気抵抗を考えなかった場合は、本当に振り子の周期は振幅に依存しないのだろうか。
では、ここからは振り子の周期の式を数学(もちろん高校数学の範囲を超えるものはすべて説明する)を用いて厳密に求めていこうと思う。
また、もちろんこの記事のタイトルにもあるように、最終的にプログラミング言語のpythonを用いて高校で教わる振り子の周期と厳密解との誤差を導く。

本記事を読む際の注意点

この記事は、自分がtex(数式を簡単にかけるソフト)で執筆したものをzennに転用させたものである。そのため、文章にところどころ式(1.1.1)などと書いてあるが、実際の式には番号が触れていない。
　もちろんzenn用に番号を振り直すつもりでいるが(途中までは完了)、しばらくの間はご容赦願いたい。

高校で教わる振り子の周期の式

厳密な振り子の周期を導出する前に、まずは高校で教わる振り子の式をおさらいしよう。もちろん初めて聞く方や、そんな昔のこと覚えてねーよという方にもわかりやすく解説するので、是非見ていってほしい。
　ではさっそく考察していく。最初に、単振り子について述べておきたい。単振り子の周期は式(1)のように表される。

$$(1)T = 2\pi\sqrt{\frac{L}{g}}$$

では、どうして単振り子の周期は式(1)のように表されるのだろうか。振り子の糸と鉛直線とのなす角$\theta$が微小角であるという単振り子の条件を利用して、導出する。
　まず、重力加速度g、小球の質量mを用いて、小球の重力は、

$$F = mg$$

と表される。単振り子の小球の軌跡は弧を描くため、x軸を弧の軌跡に沿うように設定する。原点を支点の真下と小球の軌跡の交点とし、右向きを正とする。x軸方向における小球の運動方程式は、

$$(2)m\frac{d^2x}{dt^2} = mgsin\theta$$

と表される。ここで、$xを振り子の腕の長さLと、\theta\mathrm{[rad]}を用いて表すと$、

$$x = L\theta$$

となり、式(2)に代入すると、

$$m\frac{d^2L\theta }{dt^2} = -mgsin\theta$$

となる。Lは定数なので、

$$mL\frac{d^2\theta }{dt^2} = -mgsin\theta$$

両辺を$mL$で割って、

$$(3)\frac{d^2\theta }{dt^2} = -\frac{g}{L}sin\theta$$

ここで$\theta$は微小角なので、

$$(4)sin\theta = \theta$$

と近似できる。式(4)を式(3)に代入して、

$$(5)\frac{d^2\theta }{dt^2} = -\frac{g}{L}\theta$$

となる。式(5)の二階微分方程式をとくと、振幅を$A$、初期位相を$a$で表すと

$$\theta (t) = Acos(\sqrt{\frac{g}{L}}t+a)$$

となり、この式は単振動を表すため、

$$\omega = \sqrt{\frac{g}{L}}$$

となる。周期$T$は、

$$T= \frac{2\pi }{\omega }$$

と、表せるため、

$$T = \frac{2\pi }{\sqrt{\frac{g}{L}}} = 2\pi\sqrt{\frac{L}{g}}$$

となり、式(1)が導出される。

厳密解の導出

さて、単振り子の周期が式(1)のようなきれいな形で表すことができたのは、式(4)で$\theta$が微小角なことを利用した近似を用いたからである。では、$\theta$の近似を用いずに、(3)の微分方程式を解いたらどんな周期の式が導出されるのだろうか。一般的に、$\theta$を近似して導出した振り子の周期を近似解、$\theta$を近似せずに導出した振り子の周期を厳密解と呼ばれている。では、厳密解を求めていく。

$$\frac{d^2\theta }{dt^2} = -\frac{g}{L}sin\theta$$

とはいっても、この二階微分方程式を解くことはやはり難しく、今回は違う視点から振り子の周期を求めることとする。
　方針としては、まず振り子の糸と鉛直角のなす角度$\theta$の範囲が、$0から$角振幅$\theta_0$の間にある時の運動について考える。$\theta$の範囲が、$0から$角振幅$\theta_0$の間にある時の運動について考えるということは、当然かかる時間は振り子の周期$T$を用いて$\frac{T}{4}$と表すことができる。そして、小球が最高点から真下に到達するまでにかかる時間$\frac{T}{4}$は、 微小な時間の変化dtを用いると式(6)のように表すことができる。

$$(6)\frac{T}{4} = \int_0^{\frac{T}{4}}dt$$

式(6)にある$\int$という記号は、インテグラルといって、積分を意味する。積分とは、簡単にいうと微小な変化を足し合わせるということであり、式(6)の$\int_0^{\frac{T}{4}}dt$は、微小な時間の変化$dt$を、0から$\frac{T}{4}$まで足しあげなさい、という意味である。さらに、微小な時間の変化$dt$を用いると、振り子の周期Tは式(5.2.8)のように表される。

$$(7)T = 4\int_0^{\frac{T}{4}}dt$$

これで、目的である$T$を求めることができる。あとは、$dt$を微小な角度の変化$d\theta$を用いて表せばよい。力学的エネルギー保存則より、最下点を位置エネルギーの基準点とした場合、

$$(8)0 + mgL(1-cos\theta_0) = \frac{1}{2}mv^2 + mgL(1-cos\theta ) \frac{1}{2}mv^2 =mgL(cos\theta - cos\theta _0)$$

となる。式(5.2.9)の左辺は小球が最高点にある時の運動エネルギーと位置エネルギーの和であり、右辺は小球が任意の位置にいる時の運動エネルギーと位置エネルギーの和を、その自転における糸と鉛直角のなす角$\theta$を用いて表している。また、速度vの定義より、

$$(9)v = \frac{dx}{dt} = \frac{d(L\theta )}{dt} = L\frac{d\theta }{dt}$$

式(11)を式(10)に代入すると、

$$\frac{1}{2}m(L\frac{d\theta}{dt})^2 = mgL(cos\theta-cos\theta_0)$$

両辺を$\frac{1}{2}m$で割って、

$$(L\frac{d\theta}{dt})^2 = 2gL(cos\theta-cos\theta_0)$$

両辺を$L^2$で割って、

$$(\frac{d\theta}{dt})^2 = 2\frac{g}{L}(cos\theta-cos\theta_0)$$

両辺の平方根をとって、

$$\frac{d\theta}{dt} = \sqrt{\frac{2g}{L}}\sqrt{cos\theta-cos\theta_0}$$

$dt$を微小な角度の変化$d\theta$を用いて表したいため、左辺に$dt$を持ってきて、

$$dt= \frac{d\theta}{\sqrt{\frac{2g}{L}}\sqrt{cos\theta-cos\theta_0}}$$

$$dt = \sqrt{\frac{L}{2g}}\frac{d\theta}{\sqrt{cos\theta-cos\theta_0}}$$

式(12)を式(5.2.8)に代入すると、

$$T = 4\sqrt{\frac{L}{2g}}\int_0^{\theta_0}\frac{d\theta}{\sqrt{cos\theta-cos\theta_0}}$$

となり、振り子の周期$T$を求めることができる。なお、式(12)を式(5.2.8)に代入する時、$dt$ではなく$d\theta$を用いているため、積分の範囲は、$\int_0^{\frac{T}{4}}$ではなく、$\int_0^{\theta_0}$になることに注意する。

厳密解の式から実際の数値を求める

さて、式(5.2.13)の積分は、これ以上簡単な形で書くことができない。しかし、この項目の目的としては、振り子の振幅と周期の関係及び、誤差原因について考察することであるため、なんとかして実際の周期の値を求めたい。
　今回のような、代数的・解析的に解くことが困難な問題で実際の値を求めるには、コンピューターなどを用いて数値計算を行う必要がある。式(5.2.13)のままの式だと、数値計算がしにくいため、数値計算がしやすい形に変更する必要がある。そのために、新たな変数を用意して、式を書き換える。このことを、変数変換という。　今回は、式(5.2.14)を満たすような変数$\phi$を用いて、式(5.2.13)を変数$\phi$の積分に変更する。なぜ式(5.2.14)を満たすような変数$\phi$を設定するかというと、数値変換をしやすいような積分の形に式(5.2.13)を変更するためである。

$$sin\frac{\theta}{2} = sin\frac{\theta_0}{2}\times sin\phi$$

変数変換をする上で、忘れがちだが大切なのが、範囲を考えることである。今回の場合は、$\theta$の範囲は0から$\theta_0$のため、式(5.2.14)に$\theta = 0、\theta = \theta_0$を代入すると、変数$\phi$の範囲は、$0$から$\frac{\pi}{2}$までとわかる。

では、式(5.2.13)において変数$\theta$を変数$\phi$の式に変換していく。

$$sin^2\frac{\theta}{2} = \frac{1-cos\theta}{2}$$

半角の公式(5.2.15)より、

$$cos\theta = 1 - 2sin^2\frac{\theta}{2} cos\theta_0 = 1 - 2sin^2\frac{\theta_0}{2}$$

式(5.2.16)、式(5.2.17)より、

$$cos\theta - cos\theta_0 = 2(sin^2\frac{\theta_0}{2} - sin^2\frac{\theta}{2})$$

となる。式(5.2.14)を式(5.2.18)に代入して、

$$cos\theta - cos\theta_0 = 2(sin^2\frac{\theta_0}{2} - sin^2\frac{\theta_0}{2}\times sin^2\phi) = 2sin^2\frac{\theta_0}{2}(1-sin^2\phi) = 2sin^2\frac{\theta_0}{2}(cos^2\phi)$$

となる。式(5.2.19)に整理しておく。

$$cos\theta - cos\theta_0 = 2sin^2\frac{\theta_0}{2}(cos^2\phi)$$

さて、式(5.2.19)より、式(5.2.13)の積分の$cos\theta - cos\theta_0$の部分の変換が完了した。次に、$d\theta$を$d\phi$を用いて表したい。
　基本的には、式(5.2.14)が変数$\theta$と変数$\phi$を結びつける式なため、式(5.2.14)から$d\theta$と$d\phi$の変換の式を導出したい。
　さて、$d\theta$ということは、式を$\theta$で微分すれば導出できそうである。しかし、$d\phi$にも結びつけたいので、式を$\phi$でも微分する必要がある。２つ以上の変数で微分したいときには、全微分というものを使う。２変数関数$f(x,y)$における全微分の定義は、式(5.2.20)のように表される。

$$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$$

式(5.2.20)に使用されている、$\partial$という記号は、ラウンドディーと読み、偏微分を表す。偏微分とは、1つの変数にだけ注目し、それ以外は定数として扱って微分することである。たとえば、$\frac{\partial f}{\partial x}$の場合は、$y$は変数ではなく、1や2のような定数とみなして$f$を$x$で微分する。
　では、(5.2.14)を全微分する。また、$\theta_0$は変数ではなく、定数であることに注意する。
% ここなんでこの式になるのかわからん。全微分するとは？両辺を？

$$\frac{1}{2}cos\frac{\theta}{2}d\theta = sin\frac{\theta_0}{2}cos\phi d\phi$$

$d\theta$について整理して、

$$d\theta = \frac{sin\frac{\theta_0}{2}cos\phi d\phi}{\frac{1}{2}cos\frac{\theta}{2}} = \frac{2sin\frac{\theta_0}{2}}{\sqrt{1-sin^2\frac{\theta}{2}}}cos\phi d\phi$$

式(5.2.14)を代入すると、

$$d\theta = \frac{2sin\frac{\theta_0}{2}}{\sqrt{1-sin^2\frac{\theta_0}{2}sin^2\phi}}cos\phi d\phi$$

式(5.2.21)より、$d\theta$を変数$d\phi$の式へ変換することに成功した。
　数値計算がしにくい周期の式(5.2.13)に式(5.2.19)、式(5.2.21)を代入すると、

$$T = 4\sqrt{\frac{L}{2g}}\int_0^{\theta_0}\frac{d\theta}{\sqrt{cos\theta-cos\theta_0}} = 4\sqrt{\frac{L}{2g}}\int_0^{\frac{\pi}{2}}\frac{1}{\sqrt{2sin^2\frac{\theta_0}{2}(cos^2\phi)}}\times\frac{2sin\frac{\theta_0}{2}}{\sqrt{1-sin^2\frac{\theta_0}{2}sin^2\phi}}cos\phi d\phi = 4\sqrt{\frac{L}{2g}}\int_0^{\frac{\pi}{2}}\frac{\sqrt{2}}{\sqrt{1-sin^2\frac{\theta_0}{2}sin^2\phi}}d\phi$$

$$T = 4\sqrt{\frac{L}{g}}\int_0^{\frac{\pi}{2}}\frac{d\phi}{\sqrt{1-sin^2\frac{\theta_0}{2}sin^2\phi}}$$

となる。式(5.2.22)より、式(5.2.13)の変数$\theta$を変数$\phi$に完全に置き換えることに成功した。つまり、式(5.2.22)について解けば、振り子の周期$T$の実際の値を計算することが可能になる。
　当然のことだが、数値計算をしやすくするために変数変換を行ったのだから、式(5.2.22)は容易に数値計算を行えるはずである。なんと式(5.2.22)の積分の部分は第一種完全楕円積分と呼ばれている積分で、テイラー展開やウォリスの公式を用いることで無限級数の形に変換することができる。
　では、実際に式(5.2.22)の積分部分の式(5.2.23)を数値計算が容易な式に変換していく。

$$\int_0^{\frac{\pi}{2}}\frac{d\phi}{\sqrt{1-sin^2\frac{\theta_0}{2}sin^2\phi}}$$

まず、式(5.2.23)の一部分をテイラー展開して、テイラー級数を求める。
　その前に、テイラー展開について説明しよう。テイラー展開とは、ある関数$f(x)$を多項式の形に変換するための手法のことをいう。実際にある関数($f(x)$)をテイラー展開すると、

$$f(x) = k_0 + k_1(x-a) + k_2(x-a)^2 + k_3(x-a)^3 + \cdots$$

式(5.2.24)のように表すことができる。なお、$k_0、k_1、k_2、\cdots$と、$a$は定数であり、その関数に由来する。
　テイラー展開とウォリスの公式についてはいまいち理解できないため省略するが、式(5.2.22)は式(5.2.23)のように表すことができる。また、(5.2.24)のように展開された式のことを、テイラー級数と呼ぶ。テイラー展開とは、関数をテイラー級数に変換すること、と言い換える事もできる。また、式(5.2.24)を$\Sigma$を用いて表すと、式(5.2.25)のようになる。式(5.2.25)に用いられている$f^{n}$という記号は、関数$f(x)$を$x$で$n$回微分するという意味である。また、よく形式的に、微分を$'$(ダッシュ)を用いて表す。例えば、$f'$は関数$f(x)$を$x$で一回微分したことを表し、$f''$は関数$f(x)$を$x$で二回微分したことを表す。

$$f(x) = \sum_{n=0}^\infty\frac{f^{(n)}(a)}{n!}(x-a)^n$$

ちなみに、物理で近似するときによく出てくる式(5.2.26)で表されるマクローリン展開とは、テイラー展開の特殊なバージョンである。つまり、テイラー展開の定数$a$が0の場合を示す。

$$f(x) = \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}x^n$$

式(5.2.26)のマクローリン展開は、式(5.2.5)で行った$sin\theta$と$\theta$の近似にも用いられている。
　$sin\theta$をマクローリン展開してみる。$f(\theta) = sin\theta$とおくと、式(5.2.26)より、

$$f(\theta) = \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}\theta^n = f(0) + \frac{f'(0)}{1!}\theta + \frac{f''(0)}{2!}\theta^2 + \frac{f'''(0)}{3!}\theta^3 + \cdots$$

となる。ここで、$f(\theta) = sin\theta$なため、$f^{n}(0)$は、次のような値に変換できる。

$$f(0) = sin0 = 0 f'(0) = cos0 = 1 f''(0) = -sin0 =0 f'''(0) = -cos0 = -1 \vdots$$

$f^{n}(0)$に、これらの値を代入すると、式(5.2.27)は、式(5.2.28)のように変換できる。

$$f(\theta) = 0 + \frac{1}{1!}\theta + \frac{0}{2!}\theta^2 + \frac{-1}{3!}\theta^3 + \cdots$$

式(5.2.28)を整理すると、$sin\theta$は、式(5.2.29)のように表すことができる。

$$sin\theta = \theta - \frac{1}{3!}\theta^3 + \frac{1}{5!}\theta^5 - \frac{1}{7!}\theta^7 + \cdots$$

ここで、単振り子の場合は、$\theta$が微小角と過程したため、$\theta^3、\theta^5、\theta^7、\cdots$が含まれる項を無視することができる。そのため、

$$sin\theta = \theta$$

と近似することができるのである。
　では、話を戻して、式(5.2.23)の一部分をテイラー展開してみよう。式(5.2.23)は、指数を使って式(5.2.30)のように変換できる。

$$\int_0^{\frac{\pi}{2}} (1-sin^2\frac{\theta_0}{2}sin^2\phi)^{-\frac{1}{2}}d\phi$$

$sin\frac{\theta_0}{2}$を$k$を用いて表すと、式(5.2.30)は式(5.2.31)のように表せる。

$$\int_0^{\frac{\pi}{2}} (1-k^2sin^2\phi)^{-\frac{1}{2}}d\phi$$

$k$は0から1の範囲ということに注意する。では、式(5.2.31)の一部分をテイラー展開してみる。一部分とは、式(5.2.32)のことである。

$$(1-k^2sin^2\phi)^{-\frac{1}{2}}$$

だが、いきなり式(5.2.32)をテイラー展開するのは、少々非効率なため、まずは式(5.2.33)をマクローリン展開する。

$$f(x) = (1-x)^{-\frac{1}{2}}$$

式(5.2.26)より、

$$f(x) = \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}x^n = f(0) + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \cdots$$

となる。$f(x) = (1-x)^{-\frac{1}{2}}$なため、$f^{n}(0)$は、次のような値に変換できる。

$$f(0) = (1)^{-\frac{1}{2}} = 1 f'(0) = -\frac{1}{2}(1-0)^{-\frac{3}{2}}(-1) = -\frac{1}{2}(1)^{-\frac{3}{2}}(-1) = \frac{1}{2} f''(0) = -\frac{3}{4}(1-0)^{-\frac{5}{2}}(-1)= -\frac{3}{4}(1)^{-\frac{5}{2}}(-1) = \frac{3}{4} f'''(0) = -\frac{15}{8}(1-0)^{-\frac{7}{2}}(-1) = -\frac{15}{8}(1)^{-\frac{7}{2}}(-1) = \frac{15}{8} \vdots$$

$f^{n}(0)$にこれらの値を代入すると、式(5.2.34)は、式(5.2.35)のように表すことができる。

$$f(x) = 1 + \frac{\frac{1}{2}}{1!}x + \frac{\frac{3}{4}}{2!}x^2 + \frac{\frac{15}{8}}{3!}x^3$$

式(5.2.35)を整理すると、$(1-x)^{-\frac{1}{2}}$は、式(5.2.36)のように表すことができる。

$$(1-x)^{-\frac{1}{2}} = 1 + \frac{1}{2}x + \frac{3}{8}x^2 + \frac{5}{16}x^3 + \cdots$$

さて、今回は、式(5.2.32)をマクローリン展開したいので、式(5.2.36)に式(5.2.37)を代入する。

$$x = k^2sin^2\phi$$

そうすると、式(5.2.38)のようになり、$\Sigma$を用いて式(5.2.38)を変形すると、式(5.2.39)になる。

$$(1 - k^2sin^2\phi)^{-\frac{1}{2}} = 1 + \frac{1}{2}k^2sin^2\phi + \frac{3}{8}k^4sin^4\phi^2 + \frac{5}{16}k^6sin^6\phi^3 + \cdots$$

$$(1 - k^2sin^2\phi)^{-\frac{1}{2}} = 1 + \sum_{n=1}^\infty\frac{(2n-1)!!}{2^n}\frac{(k^2sin^2\phi)^n}{n!}$$

式(5.2.39)の中で用いられている$!!$という記号は、二重階乗と呼ばれ、自然数に対して一つおきに階乗をとるという意味である。例えば、式(5.2.40)のようになる。

$$5!!= 5\times3\times1 = 15$$

では、式(5.2.32)をテイラー展開することができたため、式(5.2.39)を式(5.2.31)に代入する。そうすると、式(5.2.31)は式(5.2.41)のように表すことができる。

$$\int_0^{\frac{\pi}{2}} (1-k^2sin^2\phi)^{-\frac{1}{2}}d\phi = \int_0^{\frac{\pi}{2}} \biggl(1 + \sum_{n=1}^\infty\frac{(2n-1)!!}{2^n}\frac{(k^2sin^2\phi)^n}{n!}\biggr)d\phi$$

式(5.2.41)の括弧の中をそれぞれ積分する。まずは、1を積分して、

$$\int_0^{\frac{\pi}{2}}1d\phi = \frac{\pi}{2}$$

次に、$\sum_{n=1}^\infty\frac{(2n-1)!!}{2^n}\frac{(k^2sin^2\phi)^n}{n!}$を積分する。式(5.2.43)のようになる。

$$\int_0^{\frac{\pi}{2}} \biggl(\sum_{n=1}^\infty\frac{(2n-1)!!}{2^n}\frac{(k^2sin^2\phi)^n}{n!}\biggr)d\phi$$

定数を前に出して、

$$\int_0^{\frac{\pi}{2}} \biggl(\sum_{n=1}^\infty\frac{(2n-1)!!}{2^n}\frac{(k^2sin^2\phi)^n}{n!}\biggr)d\phi=\sum_{n=1}^\infty\frac{(2n-1)!!}{2^nn!}k^{2n}\int_0^{\frac{\pi}{2}}sin^{2n}\phi d\phi$$

式(5.2.44)に含まれる、$2^nn!$の部分は、式(5.2.45)のように変換できる。

$$2^nn! = 2n\times 2(n-1)\times 2(n-2)\times\cdots = (2n)!!$$

よって、式(5.2.44)の右辺は、式(5.2.46)のように表される。

$$\sum_{n=1}^\infty\frac{(2n-1)!!}{(2n)!!}k^{2n}\int_0^{\frac{\pi}{2}}sin^{2n}\phi d\phi$$

では、式(5.2.46)の中の積分の部分、式(5.2.47)を解く。

$$\int_0^{\frac{\pi}{2}}sin^{2n}\phi d\phi$$

式(5.2.47)を解くために、式(5.2.48)に示されるウォリスの公式を用いる。なお、式(5.2.48)は、$n$が偶数の場合の公式である。

$$I_n = \int_0^{\frac{\pi}{2}}sin^nxdx = \frac{(n-1)!!}{n!!}\frac{\pi}{2}$$

式(5.2.47)の場合、式(5.2.48)の$n$に相当する部分の値が、$2n$である。$n$が偶数であるため、式(5.2.48)を利用して、式(5.2.49)のように表すことができる。

$$\int_0^{\frac{\pi}{2}}sin^{2n}\phi d\phi = \frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}$$

よって、式(5.2.47)を解くことができたため、式(5.2.49)を式(5.2.46)に代入すると、式(5.2.50)のように表せる。

$$\sum_{n=1}^\infty\frac{(2n-1)!!}{(2n)!!}k^{2n}\int_0^{\frac{\pi}{2}}sin^{2n}\phi d\phi = \sum_{n=1}^\infty\frac{(2n-1)!!}{(2n)!!}k^{2n}\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}$$

式(5.2.50)より、式(5.2.43)を解くことができた。1を積分した式(5.2.42)と式(5.2.50)を用いて式(5.2.41)を表すと、式(5.2.51)のようになる。

$$\int_0^{\frac{\pi}{2}} \biggl(1 + \sum_{n=1}^\infty\frac{(2n-1)!!}{2^n}\frac{(k^2sin^2\phi)^n}{n!}\biggr)d\phi = \frac{\pi}{2} + \sum_{n=1}^\infty\frac{(2n-1)!!}{(2n)!!}k^{2n}\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}$$

式(5.2.51)を$\frac{\pi}{2}$でくくると、式(5.2.52)と表せる。

$$\frac{\pi}{2} + \sum_{n=1}^\infty\frac{(2n-1)!!}{(2n)!!}k^{2n}\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}=\frac{\pi}{2}\biggl(1 + \sum_{n=1}^\infty\biggl(\frac{(2n-1)!!}{(2n)!!}\biggr)^2k^{2n}\biggr)$$

また、式(5.2.52)の括弧の中に注目すると、$\Sigma$の範囲を$n=0$から$\infty$に広げることで、式(5.2.53)と表すことができる。

$$\frac{\pi}{2}\biggl(1 + \sum_{n=1}^\infty\biggl(\frac{(2n-1)!!}{(2n)!!}\biggr)^2k^{2n}\biggr) = \frac{\pi}{2}\sum_{n=0}^\infty\biggl(\frac{(2n-1)!!}{(2n)!!}\biggr)^2k^{2n}$$

なぜ式(5.2.53)のように変形できるを説明する。式(5.2.54)に$n=0$を代入すると、式(5.2.55)のように表すことができる。式(5.2.55)の結果は1になるため、式(5.2.52)は式(5.2.53)に変換することができる。

$$\biggl(\frac{(2n-1)!!}{(2n)!!}\biggr)^2k^{2n}$$

$$\biggl(\frac{(2(0)-1)!!}{(2(0))!!}\biggr)^2k^{2(0)}$$

この時、$0!!=1$、$-1!!=1$に注意する。また、$k^0=1$である。
　さて、これで式(5.2.31)を、式(5.2.53)に変換することができた。式(5.2.56)に整理しておく。

$$\int_0^{\frac{\pi}{2}} (1-k^2sin^2\phi)^{-\frac{1}{2}}d\phi = \frac{\pi}{2}\sum_{n=0}^\infty\biggl\{\frac{(2n-1)!!}{(2n)!!}\biggl\}^2k^{2n}$$

今回、求めたかった周期の式(5.2.22)に式(5.2.56)を代入すると、

$$T = 4\sqrt{\frac{L}{g}}\int_0^{\frac{\pi}{2}}\frac{d\phi}{\sqrt{1-sin^2\frac{\theta_0}{2}sin^2\phi}} = 4\sqrt{\frac{L}{g}}\frac{\pi}{2}\sum_{n=0}^\infty\biggl\{\frac{(2n-1)!!}{(2n)!!}\biggl\}^2k^{2n} = 2\pi\sqrt{\frac{L}{g}}\sum_{n=0}^\infty\biggl\{\frac{(2n-1)!!}{(2n)!!}\biggl\}^2k^{2n}$$

になる。なお、$sin\frac{\theta_0}{2} = k$であることに注意する。
　よって、振り子の周期$T$は、$k$をもとにもどして、式(5.2.57)のように表せる。

$$T = 2\pi\sqrt{\frac{L}{g}}\sum_{n=0}^\infty\biggl\{\frac{(2n-1)!!}{(2n)!!}\biggl\}^2\biggl(sin\frac{\theta_0}{2}\biggl)^{2n}$$

式(5.2.57)を用いることで、式(5.2.22)の形では求めることが困難であった周期$T$の値を、数値計算を用いて計算することが可能になった。

pythonプログラミングを用いて近似解と厳密解の誤差を求める

ここで最初に注目したいのが、式(5.2.57)に示される振り子の周期$T$の厳密解と、式(5.2.1)に示される近似解の比較である。式(5.2.1)で求められる振り子の周期の値を$T_0$とすると、

$$T_0 = 2\pi\sqrt{\frac{L}{g}}$$

$$T = 2\pi\sqrt{\frac{L}{g}}\sum_{n=0}^\infty\biggl\{\frac{(2n-1)!!}{(2n)!!}\biggl\}^2\biggl(sin\frac{\theta_0}{2}\biggl)^{2n}$$

厳密解と近似解の誤差について調べたいので、厳密解$T$を近似解$T_0$で割る。

$$\frac{T}{T_0} = \sum_{n=0}^\infty \biggl\{\frac{(2n-1)!!}{(2n)!!}\biggl\}^2\biggl(sin\frac{\theta_0}{2}\biggl)^{2n}$$

よって、厳密解$T$と近似解$T_0$の誤差を、式(5.2.58)で表すことができた。
　式(5.2.58)からわかるように、厳密解$T$は近似解$T_0$よりも必ず大きな値になる。
　では、実際に式(5.2.58)の$\theta_0$に様々な値を入れて、誤差がどの程度生じるのかを数値計算で求めてみよう。

$$\sum_{n=0}^\infty\biggl\{\frac{(2n-1)!!}{(2n)!!}\biggr\}^2\biggl(sin\frac{\theta_0}{2}\biggl)^{2n} = 1 + \frac{1}{4}sin^2\frac{\theta_0}{2} + \frac{9}{64}sin^4\frac{\theta_0}{2} + \frac{225}{2304}sin^6\frac{\theta_0}{2} + \cdots$$

どうやるのかというと、式(5.2.58)を式(5.2.59)に変換して、いくつかの値を$\theta_0$に入れたときにどのくらい誤差がでるのかを調べる。
　今回は、参考までに$\theta_0$に$\frac{\pi}{24}、\frac{\pi}{12}、\frac{\pi}{6}、\frac{\pi}{4}、\frac{\pi}{3}、\frac{\pi}{2}$の計6つの値を入れることとする。ちなみに$\theta_0$の単位は$\mathrm{[rad]}$である。わかりやすいように度数法でも表すと、代入する角度は、$7.5^\circ、15^\circ、30^\circ、45^\circ、60^\circ、90^\circ$の6つである。
　では、コンピューターを用いて数値計算を行う。今回はプログラミング言語pythonを用いて、数値計算をするコードを作成した。作成したコードを以下に示す。

import sympy
import math
sum = 0
angle = 45 # ex: 45
for n in range(1000):
    i =((sympy.factorial2(2*n-1)/sympy.factorial2(2*n))**2)*((math.sin(math.radians(angle)/2)**2)**n)
    sum += i
print(sum)

上記のコードをそれぞれの角度ごとに実行した結果を表5.4にまとめた。

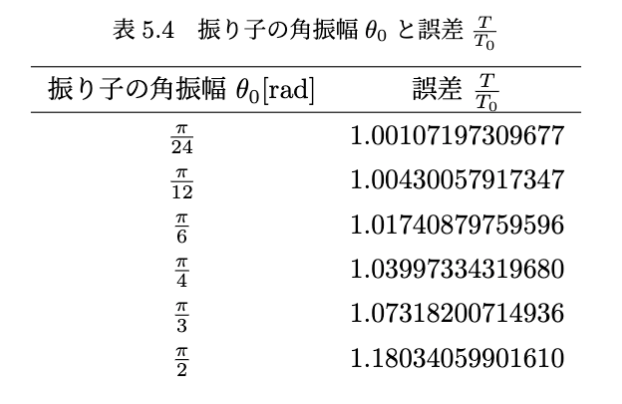
　誤差を相対誤差$\%$で表したいので、表5.4の誤差$\frac{T}{T_0}$から1を引いて、$\times 100$した値を、表5.5にまとめる。

表5.5を参照すると、角振幅$\theta_0$の値が$45^\circ$でも、厳密解と近似解の誤差は$4\%$ほどしかないことがわかる。このことから、近似解の周期$T_0$は、厳密解の周期$T$をよく表しているといえる。今回の実験は$\theta_0$の値を$15^\circ$くらいで行ったため、理論上誤差は約0.43 $\%$生じていると考えられる。

おわりに

さて、いかがであっただろうか。まず長くなってしまったことをお詫びさせてほしい。だが、ここまで読んでくださったことに改めて感謝の念を伝えたい。
　これは実際には大学数学の内容だが、高校生でもわかるように解説したつもりである(わかりやすく書くということは、説明を多くするということであり、どうしても長くなりがちである)。もし何かわからないことがあったら是非コメント欄に書いてほしい。
　また、もしこれを読んでくれているのが高校生や大学生で、この内容をレポートに書きたいという方がおられたら、是非使用してほしい(その再は参考文献の欄にURLを載せてくださると大変喜ぶ笑)。

参考文献

おっさんの備忘録【楕円積分】,おっさんの備忘録,https://tamami8.net/2019/06/14/楕円積分

テイラー展開と近似式,高校数学の美しい物語,https://manabitimes.jp/math/1399

wikipedia【楕円積分】,wikipedia,https://ja.wikipedia.org/wiki/楕円積分

楕円積分 振り子の周期を求める,http://hooktail.sub.jp/mathInPhys/elliptical/

第一種完全楕円積分と幾何平均について,不明,http://www.tcp-ip.or.jp/~n01/math/Elliptic integral/Elliptic integral.pdf

テイラー展開とは？,controlabo,https://controlabo.com/taylor-series/

$sin^n(x),cos^n(x)$の積分【ウォリス公式】,うちノート,https://uchii-memo.hatenablog.com/entry/sin^n-cos^n-integral

振り子の等時性は正しいのか？現れる第1種完全楕円積分,ヨビノリたくみ,https://www.youtube.com/watch?v=n-wpASaO3oE

【大学数学】最小二乗法(回帰分析)【確率統計】,ヨビノリたくみ,https://www.youtube.com/watch?v=Zz1sgYxrA-k

解説 単振り子の運動,Hiromu Nakagawa,
https://www.ne.jp/asahi/tokyo/nkgw/www_2/gakusyu/rikigaku/Tanfuriko/Tanfuriko_kaisetu/Tanfuriko_kaisetu.html

単振り子の話,桂田祐史,http://nalab.mind.meiji.ac.jp/~mk/labo/text/furiko.pdf

単振り子の周期（近似解と厳密解の比較）,美しい物語,https://manabitimes.jp/math/1273

【大学数学】全微分とは何か【解析学】,ヨビノリたくみ,https://www.youtube.com/watch?v=ChoArVJnSjQ