数値計算に親しむ〜中学物理ではじめる数値計算〜

はじめに

数値計算は楽しいですが、若干敷居が高い．

以前、数値計算の入門になればと思い、いくつか記事を書きましたが、ちょっとイメージから遠かったかもしれない．

数値計算に親しむ（電磁気関連を3編）
https://qiita.com/sandshiP/items/f07f6c1443e024cb775a
https://qiita.com/sandshiP/items/27bc6ee6f079a88b0f08
https://qiita.com/sandshiP/items/2b8b10265d0c11597081

そこで、今回はもうすこし身近な（イメージしやすい）分野として、『物体の落下』を対象として問題を説いていきたいと思います。

公式と問題の整理

まずは、物体の加速度運動および等速直線運動に関する以下の2つの公式から。

\begin{align}
a = \frac{dv}{dt} \approx \frac{v(t) - v(t - \Delta t)}{\Delta t}　&…(1) \\
v = \frac{dx}{dt} \approx \frac{x(t) - x(t - \Delta t)}{\Delta t}　&…(2)
\end{align}

$a$ $[m/s^2]$は加速度、$t$ $[s]$は単位時間、$v$ $[m/s]$は速度、$x$ $[m]$は変位とします。

これら式から分かることは、「加速度は微小時間における速度の傾き」「速度は微小時間における変位の傾き」という、いわば定義のみです。

このままでは、加速度運動をする物体が $t$ 秒後、どれくらい進んでいるのかわかりませんね。

ということで、今回解きたい問題は、以下とします。
『加速度 $a$ で等加速度運動し始めた物体が、時刻 $t$ 後に移動した距離を求めよ』

中学・高校の物理を覚えていれば、あたりまえに第一式の両辺を$t$について積分して解析解を求めることが可能ですが，ここではそれはできない※こととしましょう．

※「解析解を求められない非線形問題を数値的に解くこと」が数値計算の目的であり，解析解が求められるような問題ではつまらないので

実装

今回は、可視化を容易としたいので、jupyter notebook上でpythonを用います。

パラメータの設定

はじめに、今回用いる公式、$\boldsymbol{a} = \frac{d^2}{dt^2}\boldsymbol{x}$に現れるパラメータを決定します。

dt = 0.1   # 微小時間幅 dt
a = 1.0      # 加速度 a = 1.0 [m/s^2]

A = np.full(len(T), a)
T = np.arange(0, 1.0, dt) # 時間軸の宣言
V = np.zeros(len(T))      # 速度の時系列の初期化
X = np.zeros(len(T))      # 変位の時系列の初期化

ここでは、微小時間幅$\Delta t$, 加速度$a$を定めています。
また、速度$v$, 変位$x$の初期値は$0$としました。

公式の実装

式$(1)-(2)$を用いて、以下のような速度および変位の更新式$(3)-(4)$を得ます．
数値計算においては，時間方向の更新式を得て，時間ステップを進めて解を求める手法を「陽に解く」などと言います．
逆に，各差分式から得られる連立解の行列方程式を反復法などを用いて求解する手法を「陰に解く」と言ったりして，一長一短があります．（詳細は割愛）

\begin{align}
v(t) = v(t - \Delta t) + a\Delta t &…(3) \\
x(t) = x(t - \Delta t) + v\Delta t &…(4)
\end{align}

上記の式は、最新の速度（変位）は、一瞬間前の速度（変位）に変化量を足したもので，
ここでは微小時間における速度$v$は一定であるものとして近似的に解いています。

では、こちらの更新式を実装したものが以下になります。

for t in range(1, len(T)):
    V[t] = V[t-1] + A[t] * dt # 式(3)
    X[t] = X[t-1] + V[t] * dt # 式(4)

実装した式と、用いた差分式$(3)-(4)$が対応していて見やすい．
ちなみに，julia等を使うともっと綺麗に書けます，良い言語ですね．

計算結果と厳密解の比較

では、実装した式を用いて、任意の時間経過後に物体の変位$x$を求めた結果を示します。

for t in range(1, len(T)):
    V[t] = V[t-1] + A[t] * dt
    X[t] = X[t-1] + V[t] * dt

plt.plot(T, X, marker=".", label="calc.")
plt.plot(T, 1/2*a*T**2, linestyle='-', label="theory")
plt.xlabel("time [s]")
plt.ylabel("x [m]")

plt.legend()
plt.savefig("a.png")

横軸が時間、縦軸が移動した距離としており、calc.が数値計算結果です。また、ここでは比較のために解析解theoryを示しています。
ご覧いただければ分かる通り、数値計算結果と解析解の間に、誤差が生じていることが確認できました。その一方で、数値計算結果と解析解は、時間経過とともに漸近していき、十分時間経過後には一致していることも確認できました。

いったん締め

なぜ誤差が生じるのでしょう？

これは少々長い話になってしまうので一旦ここで言いたいことを書いてしまいます。
今回は、数値解析によって、物体の加速度運動を求めました。

扱う問題が簡単であったため（誤差もあったため）、数値解析のメリットは感じにくいものとなってしまいましたが、感じていただきたいのは数値解析の単純さと応用の幅です。

単純さは、わずか数行のコードで物理現象を記述できる、ということから。
応用の幅としては、
「公式さえあれば差分化して、あとは逐次漸化式を解いていくだけで、物理現象を可視化できる」、ということから感じていただければ、と思います。

電磁気も、波動も、剛体も、流体も、あらゆる物理現象を、個人のPCの中で再現できることにロマンを感じていただければと思います。

誤差の要因を考察

では，誤差の原因を追いかけていきましょう．

計算条件をいくつか変えて試したところ同様の誤差が確認されたので、計算条件・コーナーケースによるものではなく定式化・実装において問題があるかと思われます。

そこで、定式化した式$(3)-(4)$を実装した箇所を見直してみましょう。

for t in range(1, len(T)):
    V[t] = V[t-1] + A[t] * dt # 式(3)
    X[t] = X[t-1] + V[t] * dt # 式(4)

ここで、式$(4)$の実装を行っている3行目、変位の更新式に着目し、速度Vが時刻tに対してどのように変化しているか模式図を作りました。

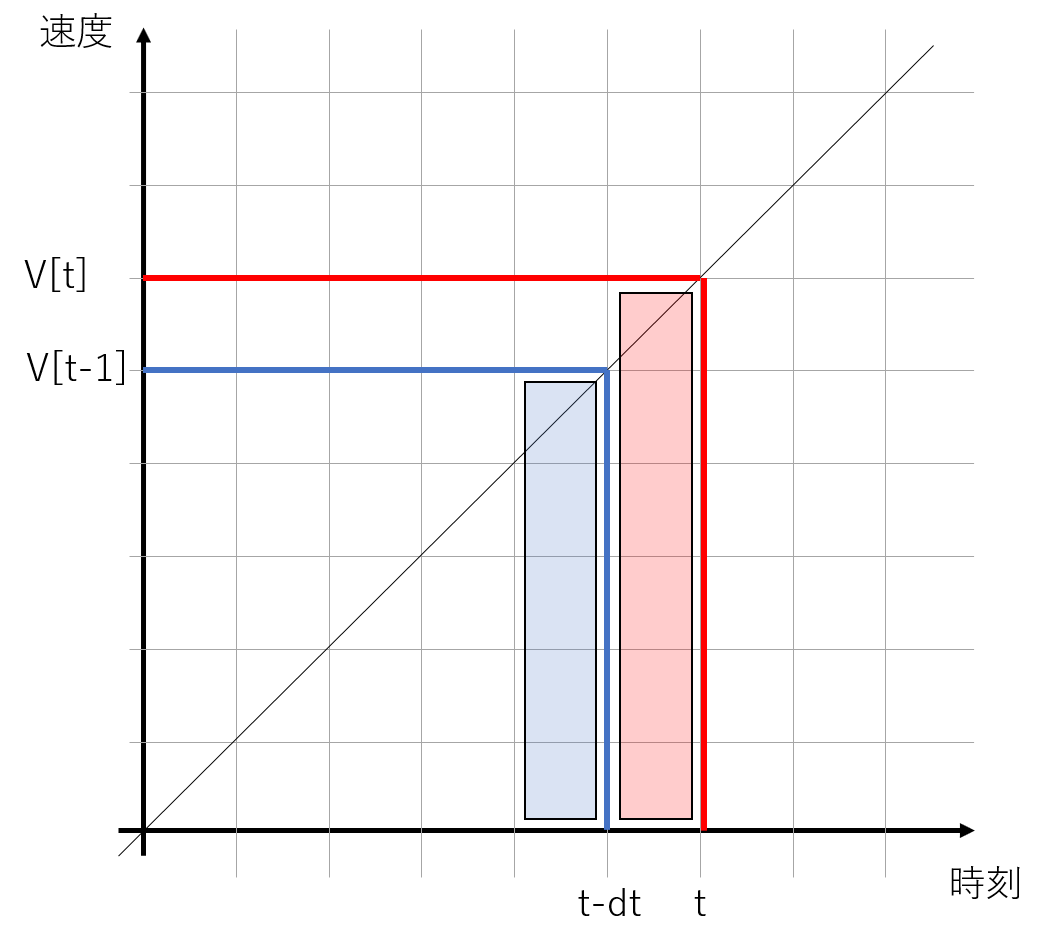
少し分かりづらい図ですが、ここで用いている速度V[t]は、$t_i < t < t_i + dt$において、実際には連続的（傾き$a$の1次関数）によって変化しますが、ここでは以下のように近似的に一定の値としています。そのため時刻tにおける厳密な速度Vを求めることはできません。

また、そのため時刻t-1~tの間に進むべく距離（横軸と縦軸の積＝面積）は、V[t] * dt（赤の領域）では大きすぎるし、V[t-1] * dt（赤の領域）では小さすぎることがわかります。

変位X[t]の更新式にV[t]かV[t-1]のいずれを用いるかは、もう少し厳密な議論が必要です。

そこで、差分法について紹介します。

差分法の比較

上記の実装では、時刻tにおける変位X[t]を求めるために、時刻tにおける速度V[t]を用いているため、図でいうところの赤の領域を求めてしまっていることがわかりました。この差分の取り方を、前進差分といいます。

一方で、時刻tにおける変位X[t]を求めるために、時刻t-1における速度V[t-1]を用いる、図でいうところの青の領域を求める差分の取り方を、後進差分といいます。

しかしながら、前進差分も後進差分も、この問題では同程度の誤差が発生することが予想できます。
そこで、前進差分'V[t]'と後進差分V[t-1]の真ん中(V[t] + V[t-1])/2を取ればよいだろう、という発想が中心差分です。

では実際に、それぞれの差分法を以下に実装しました。

for t in range(1, len(T)):
    V[t] = V[t-1] + A[t] * dt                # 式(3)

    Xf[t] = Xf[t-1] + V[t] * dt              # 式(4), 前進差分
    Xb[t] = Xb[t-1] + V[t-1] * dt            # 式(4), 後進差分
    Xm[t] = Xm[t-1] + (V[t] + V[t-1])/2 * dt # 式(4), 中心差分

それぞれ、Xfは前進(forward)差分、Xbは後進(backward)差分、Xmは中心(middle)差分によって求めた変位Xを示しています。
では実際にこちらも結果を求めてみましょう。

前進・後進差分ではやはり同程度の誤差が見られるのに対し、中心差分では数値解と解析解がほぼほぼぴったり一致していることが確認できます。

念の為、誤差の時間発展を確認しましょう。

中心差分（赤線）が常に0%の誤差で解析解と一致することが確認できました。

これは、今回用いた問題である等加速度運動において、(V[t] + V[t-1])/2 * dtが、式$(1)-(2)$を解析的に解いた際に現れる台形積分の式と一致するためです。中心差分を用いることによる利点・欠点の詳細は置いておくとして、簡単に高い精度を実現することができる、ということは強調しておきたいです。

まとめ

以上の議論によって、微分・積分といった厳密な理論を用いずに、中学校物理をチカラ技で解くことができました。今回は、簡単な問題を簡単な数値解析で解き、数値解析の簡単さを少しだけでもお伝えできていればなと思います。

次回は、今回用いた数値解析のコードを少しだけ拡張することで、
空気抵抗を考慮した落下運動、境界条件を考慮した二重振り子解析等も解ける、ということを紹介したいと思います。