競プロ典型90問 001 Yokan Party（★4）

やり方を長時間考えてしまう場合、何かを大きく変える必要がある。
2分探索、悩んだときには検討を。

重要な考え方

「mセンチでy個」が可能な場合、端からmセンチ以上の出来るだけ短い長さで区切っていくと必ずy個（以上）取れる
という考え方が重要。

一旦DPで考える

端から貪欲に切っていく方法がなぜOKなのかよくわからん、見落としはないのか、という疑問を感じる場合は、一旦DPで考えてから無駄なところを省く考え方で考えるのがよい。

1ピースの長さがm以上とする切り方をすべて網羅するのをDPで行う。各切れ目と右端に値を付ける。値はその切れ目より左に何ピース出来るかという値。これを、左端の1ピースの配置全部、左端から2ピースの配置全部…という風に網羅しながら記入する。

1. 左端からm以上の切れ目全てに1を記入。左端のピースの配置を全部網羅済。
2. 1が書かれていた切れ目からm以上右にある切れ目全てに2を記入。左端から2ピースの配置は全部網羅済。
3. 2が書かれていた切れ目からm以上右にある切れ目全てに3を記入
4. 増やせる値がなくなったら終了。右端の数字がピースの個数

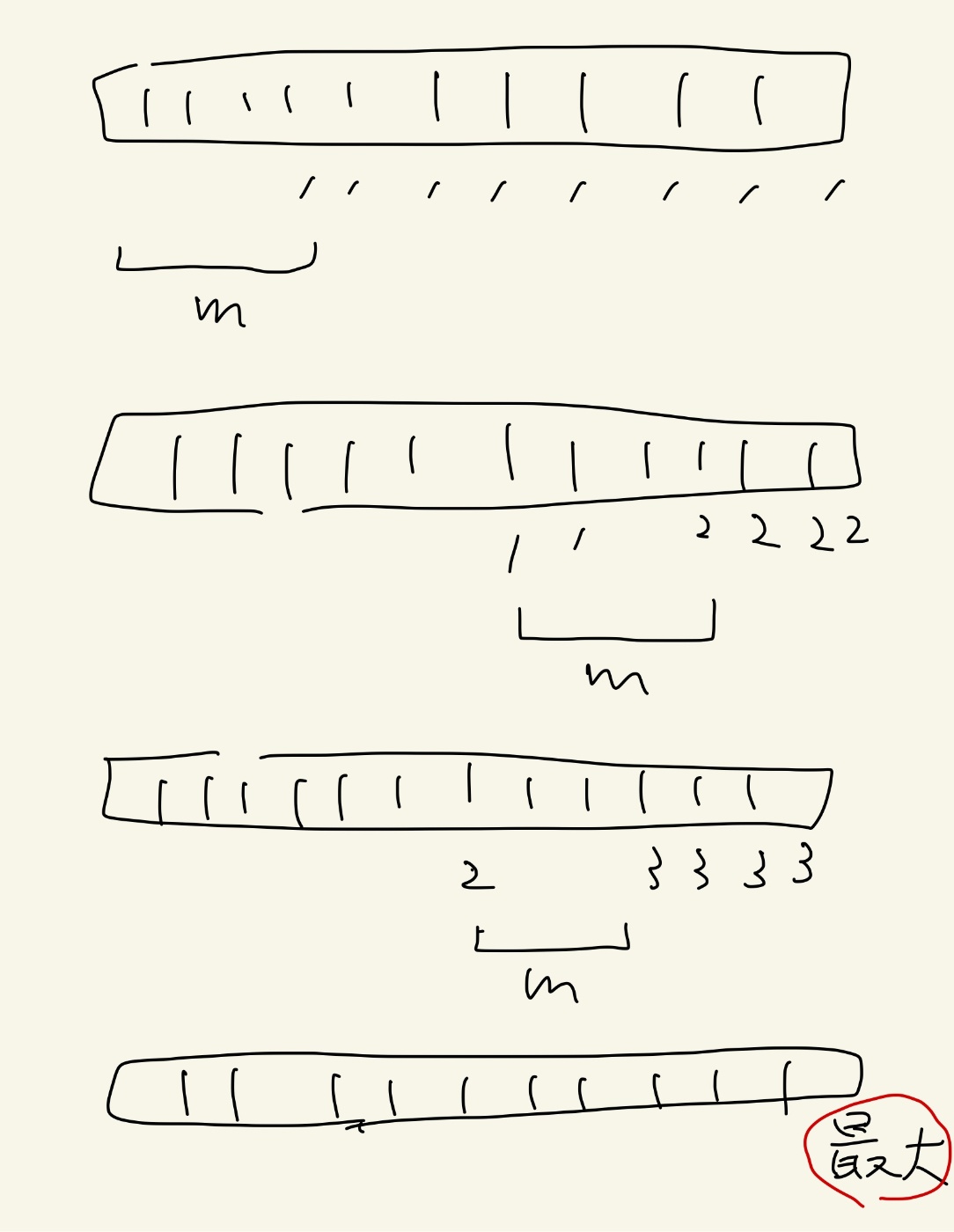
これで1ピースの長さがm以上のすべての切り方を確認できた。

実は、3を書き込むときは、一番左の2に対応する3だけ書き込めばよい。

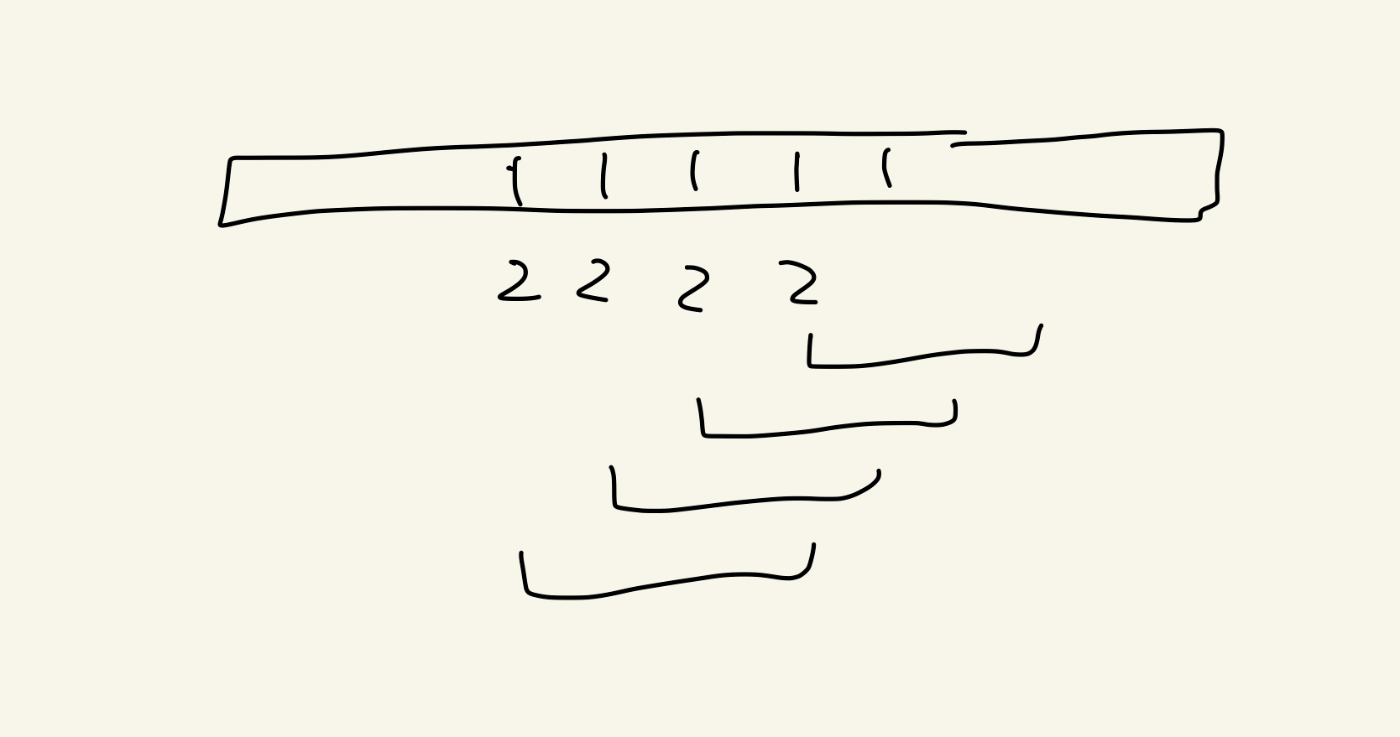
よって各段階で一番左のものだけ行えば良い。それはつまり左からm以上の最低値で貪欲に行く方法である。

2分探索で答が出たあと、その答の長さのピースが存在することの証明

2分探索で求めたものは「この値以上の長さで切ったら求める切り方が出来る」というもので、コストの「最小のピースの長さ」とは違う。そこで、2分探索で答が出たあと、その長さのピースが存在するかどうかを確認する。

2分探索で出た答をAとする
この答の切り方のすべてのピースの長さがAより大きいとすると、2分探索でAより大きな解が出てくるので2分探索の答がAであることと矛盾。よって、2分探索の解がAならAの長さを持つピースが存在する。

ピースの長さがm+1以上のとき k(目標値)個に達しないが、mにするとkを越えるとき

答はm。mで分割した後、どれかをつなげてkにすればよい。kにした後、最小のピースの長さは変わらない。kにした後、最小のピースがm’になるなら、そのm’が答えとして出てくるはずなので。

2分探索の2つのタイプ

ちなみに2分探索には

• 値を見つける
• 区切りを見つける

の2つの種類があり、実装が異なる。今回は区切りを見つける方。