競プロ典型90問 041 Piles in AtCoder Farm(★7)
図がないと何もわからんので書く。
運営による想定解法(1a, 1b, 2, 3)を図にする。
問題の概要
XY平面上のいくつかの格子点(整数x, 整数y)が与えられる。
与えられたすべての点を囲む一番短い長さの堀を作る。
堀の内側と輪郭上の格子点の数の合計を求める。(答えるのは始めに与えられる数を省いた値)
小課題1 想定解法1a
小課題1では、始めに与えられるのは3点。
3点なので、どの2点間も堀が作られる。たとえ3点が直線でも。
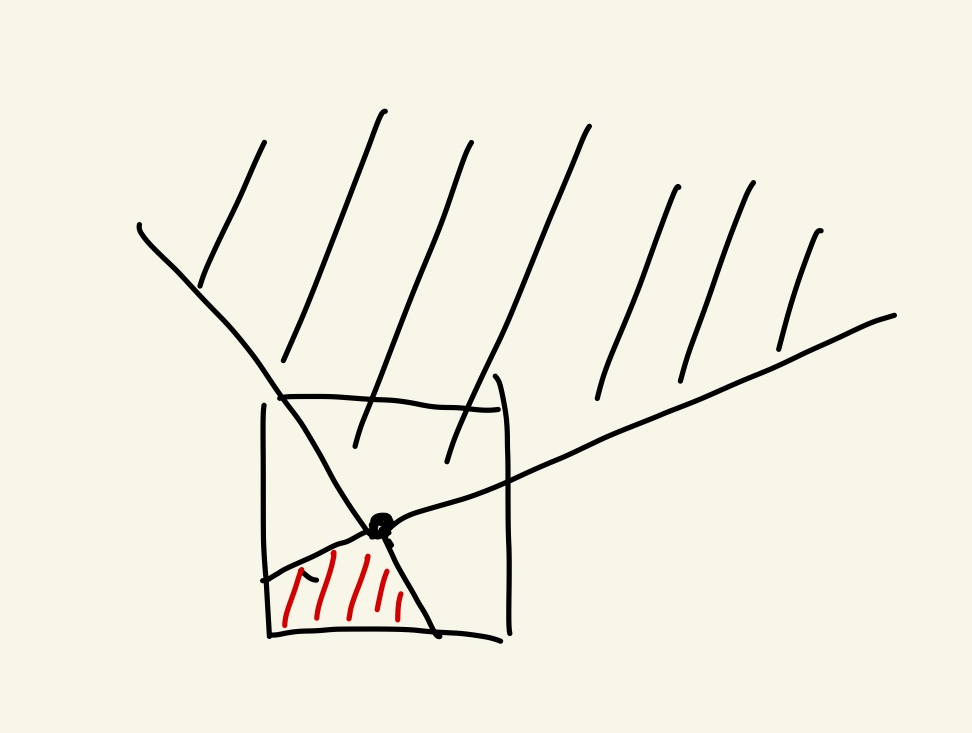
各x座標を調べる
2本ラインが通るx座標で次のように中に入る格子点を知りたい。
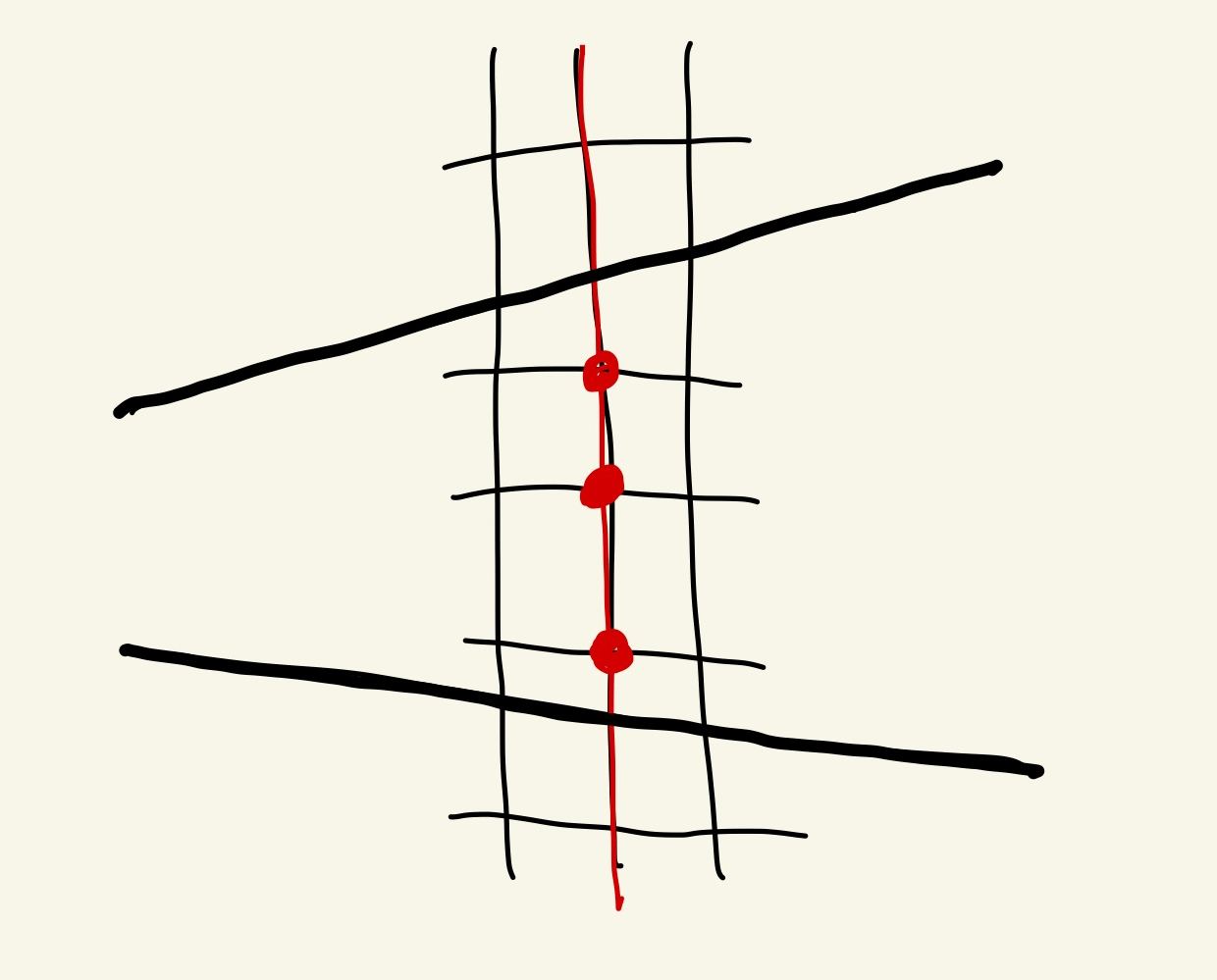
しかし、ラインを調べる際はそのラインが上側か下側か確定する前なので、
- 上側のときに必要な上限情報(一番上の格子点がどこか)
- 下側のときに必要な下限情報(一番下の格子点がどこか)
を両方記録する。

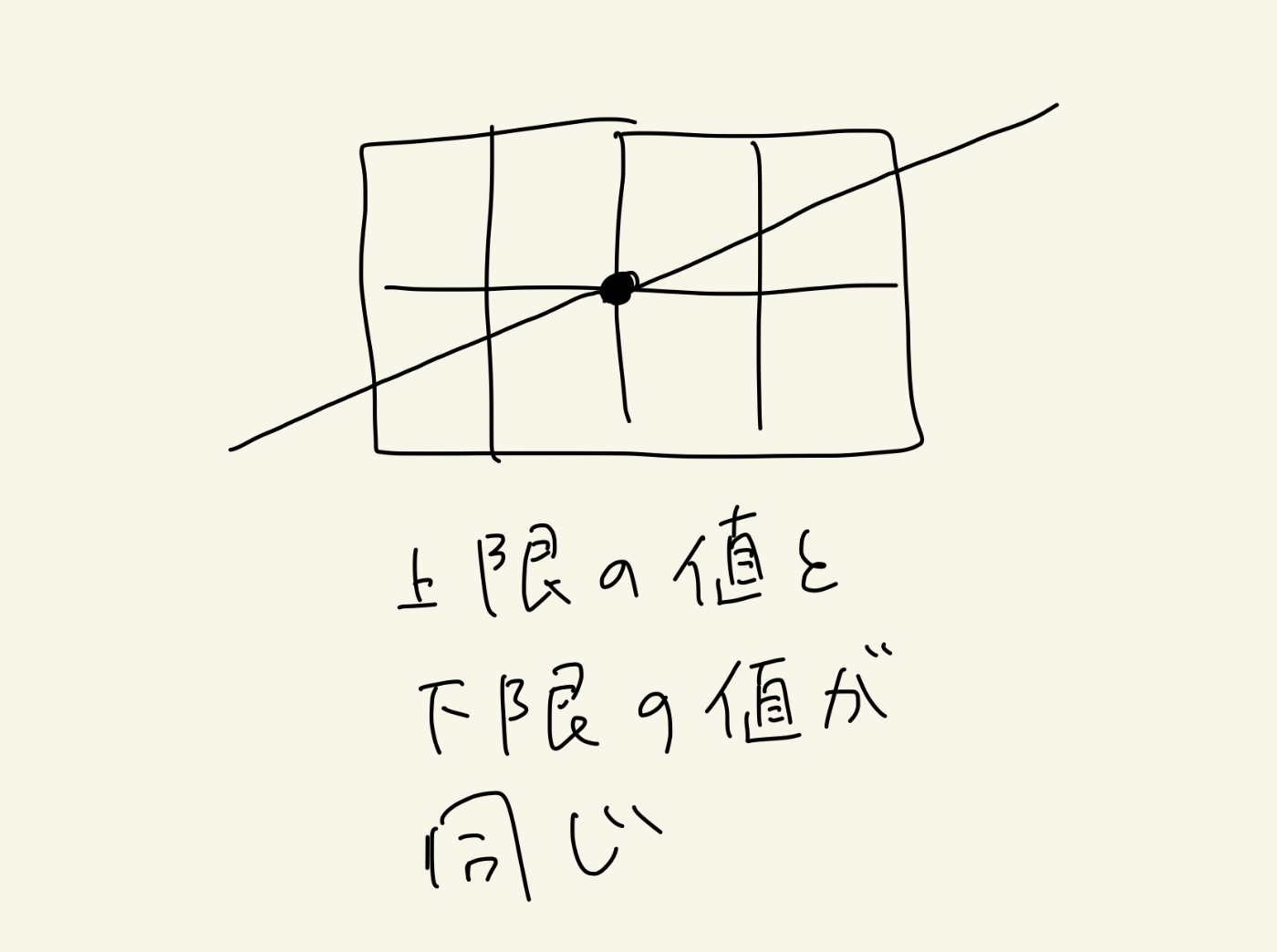
ちょうど格子点を通るときはそのラインの上限格子点と下限格子点が同じ。
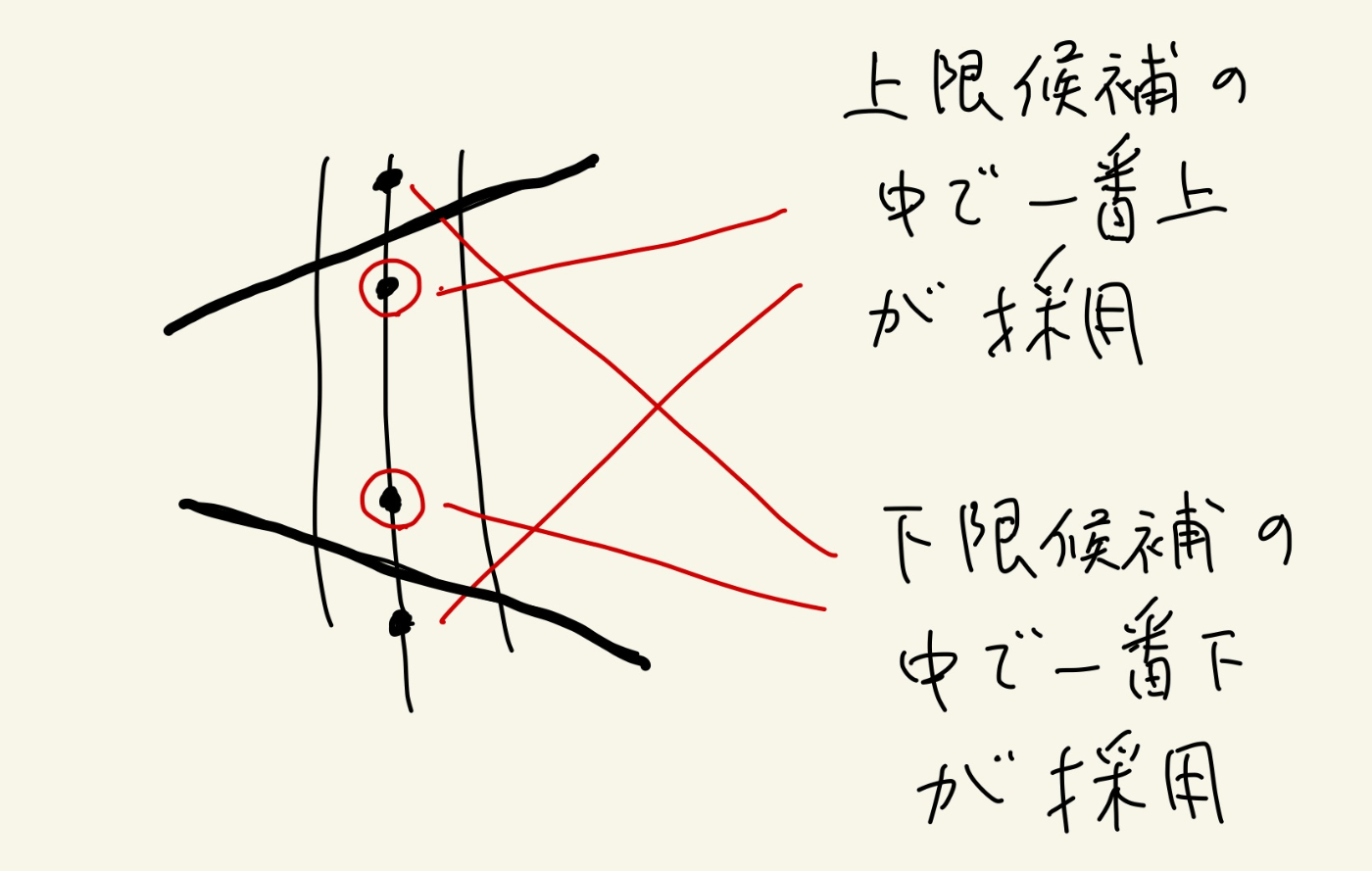
全ラインをチェックしたら情報が出そろうので
- 上側の点の最高
- 下側の点の最低
を採用する。
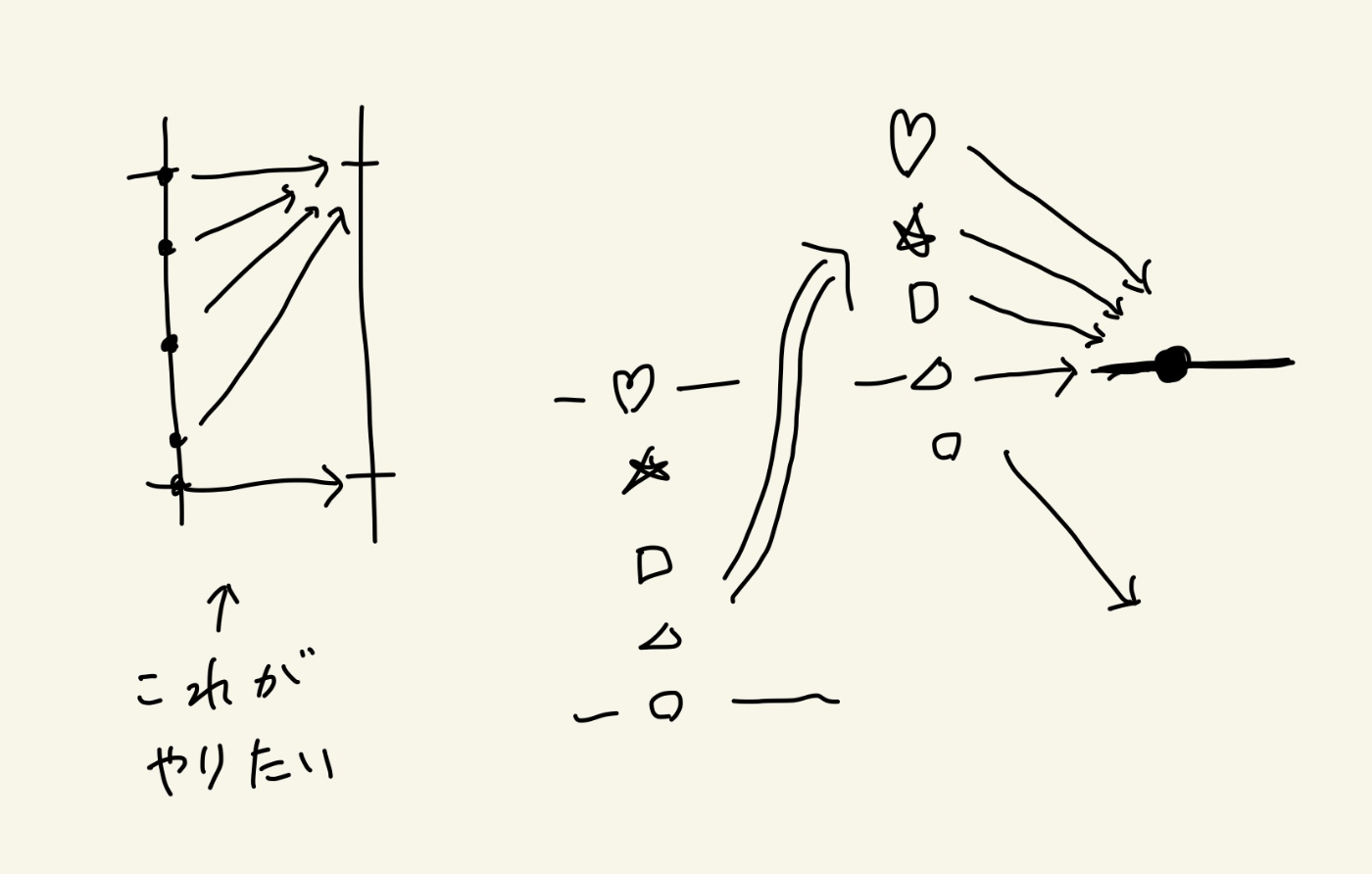
ただし、ラインがY軸に平行なら上限と下限を単純に設定する。

ここで、「下側のときに必要な値」は、y座標の値を繰り上げたい。つまり2.01なら3にしたい。このため分子に値を足す。足す値は分母から1を引いた値にすると辻褄が合う。
最後に各x座標で格子点を数えてそれを合計する。
また、与えられた点の数は引いて答えることに注意する。
小課題1 想定解法1b
引き続き与えられるのは3点。
3点が直線上なら最大と最小を比べる。格子点をいくつ通るかは最大公約数を利用する。
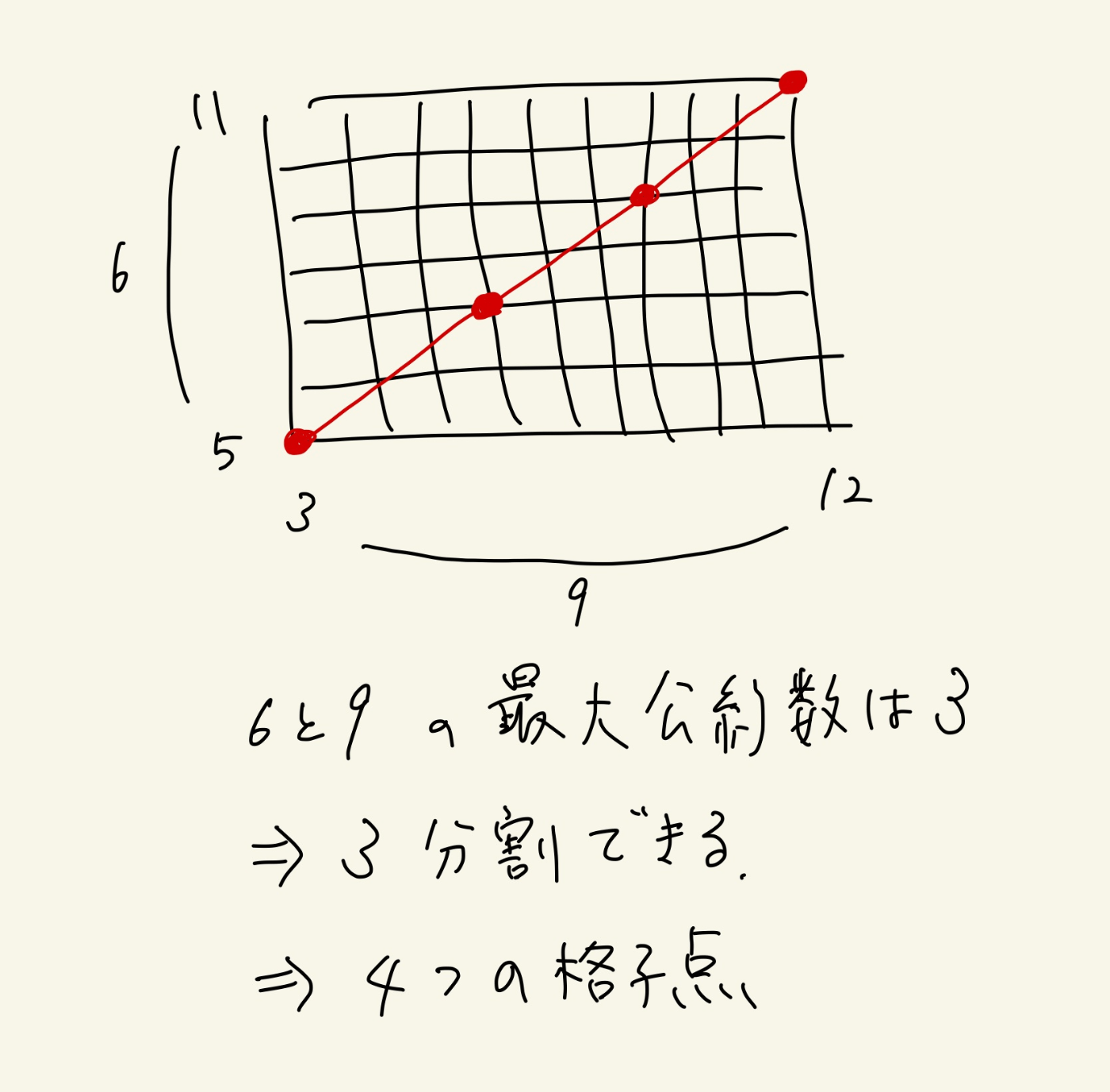
直線上にない場合を以下で述べる。
外積を用いる。crsは外積の値を出すもの。10とか-20とか値を返す。矢印のどちらかが大きさ0なら結果も0になる。

ccwは向きを返すもの。右回りなら-1を返し、左回りなら1を返す。
3点が直線上か、矢印のどちらかが0なら0。
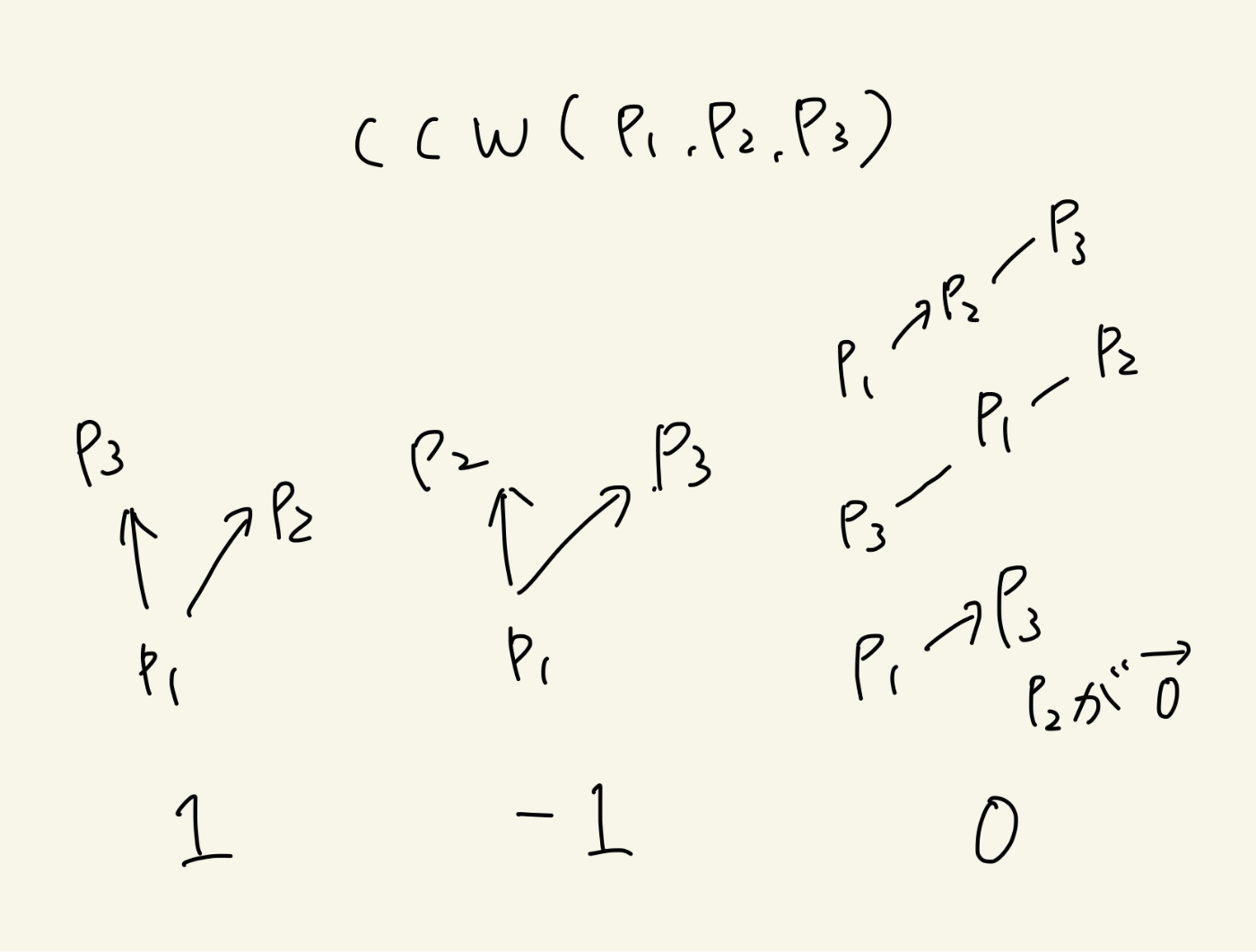
最大が1001かける1001なのですべての格子点Hで以下を調べて該当するものをカウントする。
Hの場所による次の3つのを調べる
- 1->Hと1->2のccw
- 1->Hと1->3のccw
が同じかどうか
- 2->Hと2->1のccw
- 2->Hと2->3のccw
が同じかどうか
- 3->Hと3->1のccw
- 3->Hと3->2のccw
が同じかどうか
これらが3つともすべて「異なる」であるとき、カウントする。
三角の内部と辺の途中は、上の3つはすべて「異なる」なのでカウントの対象になる。
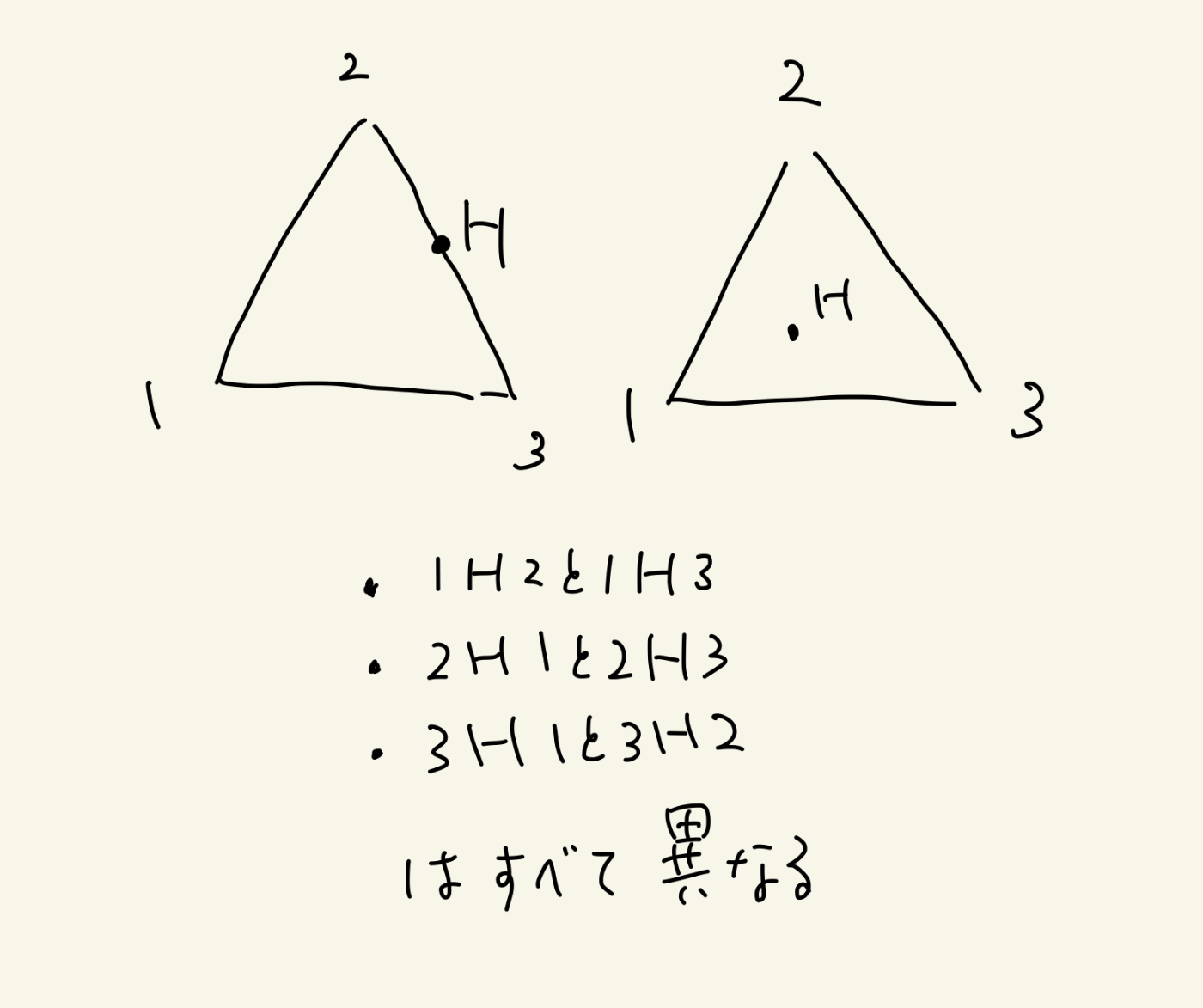
「与えられた点自身」だが、次の例では
- 1->Hと1->2のccw
- 1->Hと1->3のccw
が両方とも0になってしまい同じになる。これはカウント対象外である。
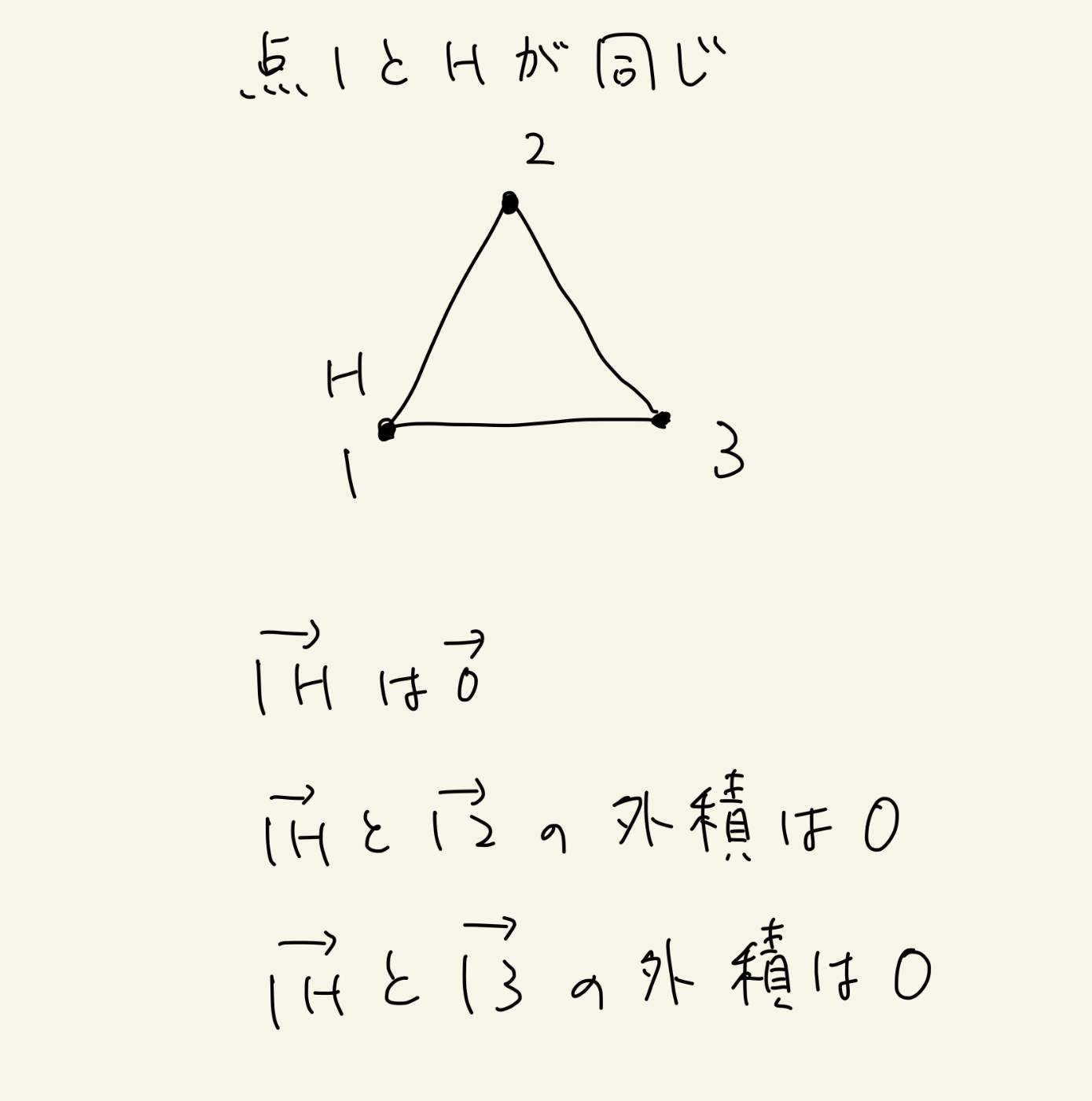
この41の問題はもともと杭が打ってあったところを省いてカウントする問題なのでカウントしなくても実はこれでつじつまがあう。
次に三角形の外側を考える。Aのところにある点は
- 1->Hと1->2のccw
- 1->Hと1->3のccw
が同じになるのでカウントしない。

線の引き方の反対のやり方を考えることにより、三角形の外側にある境界線はどこかのカウントしないエリアに含まれる。
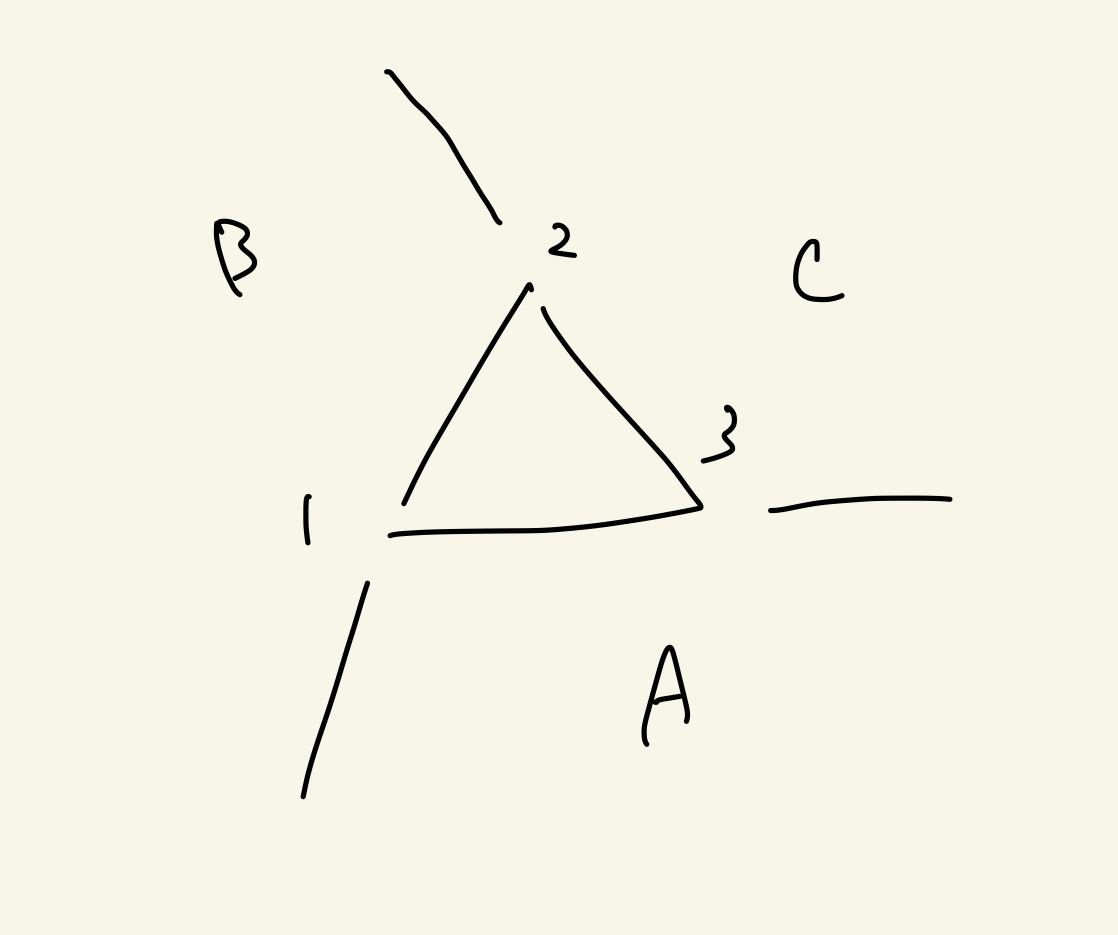

以上により三角形の外側すべてはccwの値が同じものが最低ひとつありカウント対象にならない。
小課題2
X座標,Y座標ともに0から1000までの範囲。与えられる点は多い。
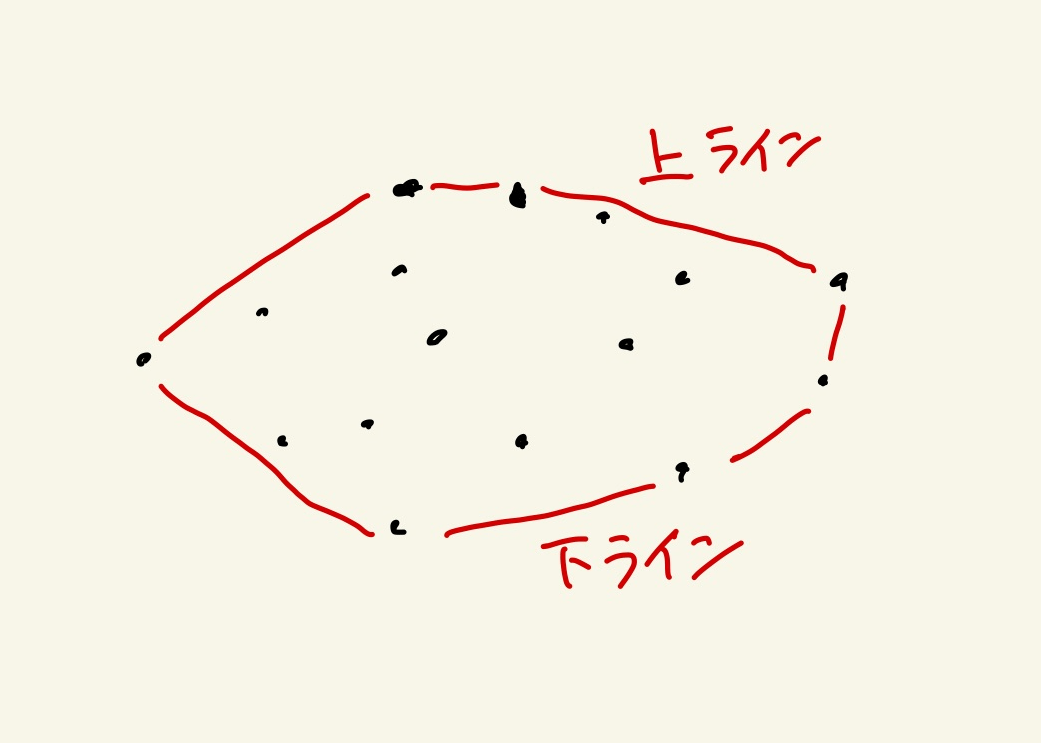
まずは
- 上ラインを作る座標の配列(想定解法のC++のコードではG2)
- 下ラインを作る座標の配列(想定解法のC++のコードではG1)
を作る。
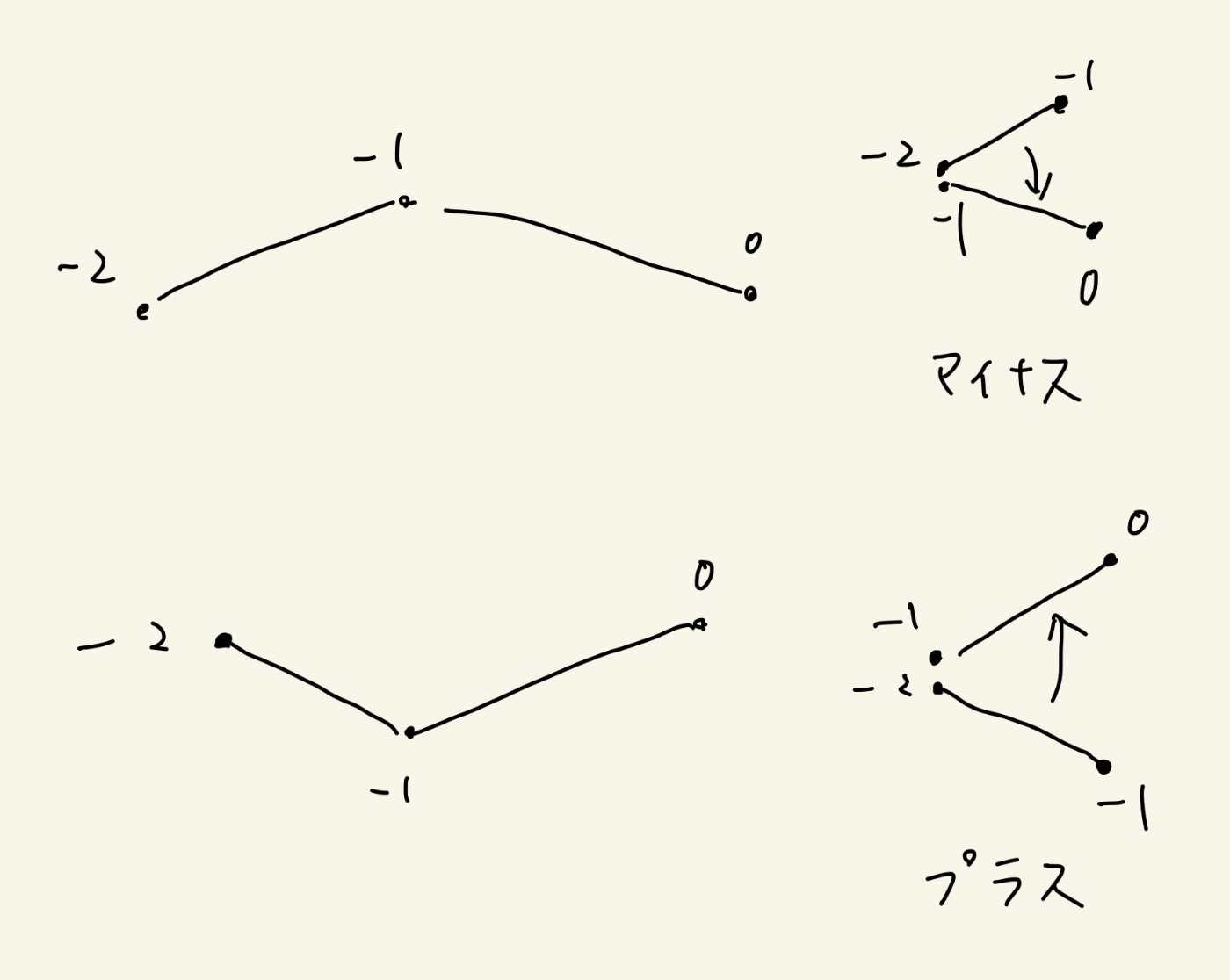
ラインの作り方は、点を追加するときにに
2つ前 — 1つ前 — 調べる点
で出来る角度を調べて1つ前がいらないなら捨ててる。
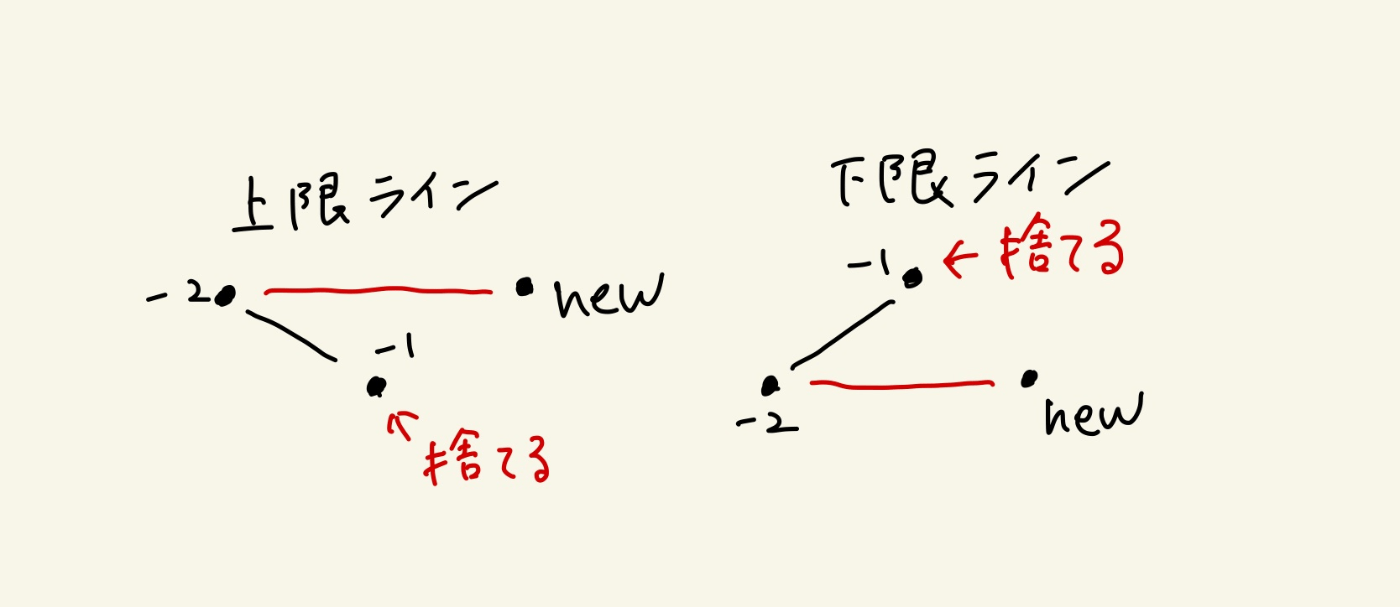
上下のラインが決まったらラインごとに
- 上ラインだったときに必要な情報
- 下ラインだったときに必要な情報
を書く。
全x座標の下限情報と上限情報を見てカウントする。
小課題3
面積と辺上の格子点の数から内部の格子点の数を計算する。
ピックの定理を使う。
ピックの定理
- 面積
- 辺上の格子点の数
- 内部の格子点の数
の関係式はピックの定理を使います。
S = i + b / 2 - 1
/*
S 面積
i 内部の格子点の数
b 辺上の格子点の数
*/
ネット上に解説はたくさんある。
ここでは割と直感的に把握できるのを紹介する。
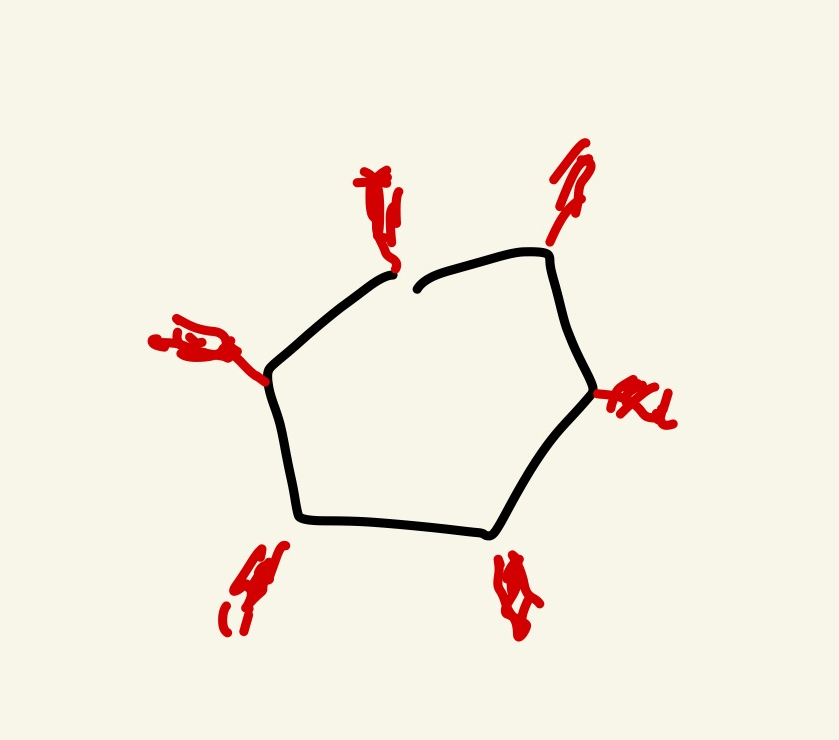
各格子点の周りに辺の長さ1の四角を書き、それがどれだけ面積に貢献するか考える。四角の内1/3が図形に含まれていればその格子点は貢献度が1/3。貢献度を全部足せば面積Sになるのを以下で確認する。ただし、外側に膨らんだ形を用いる。
辺に触れてない内部の点は当然1
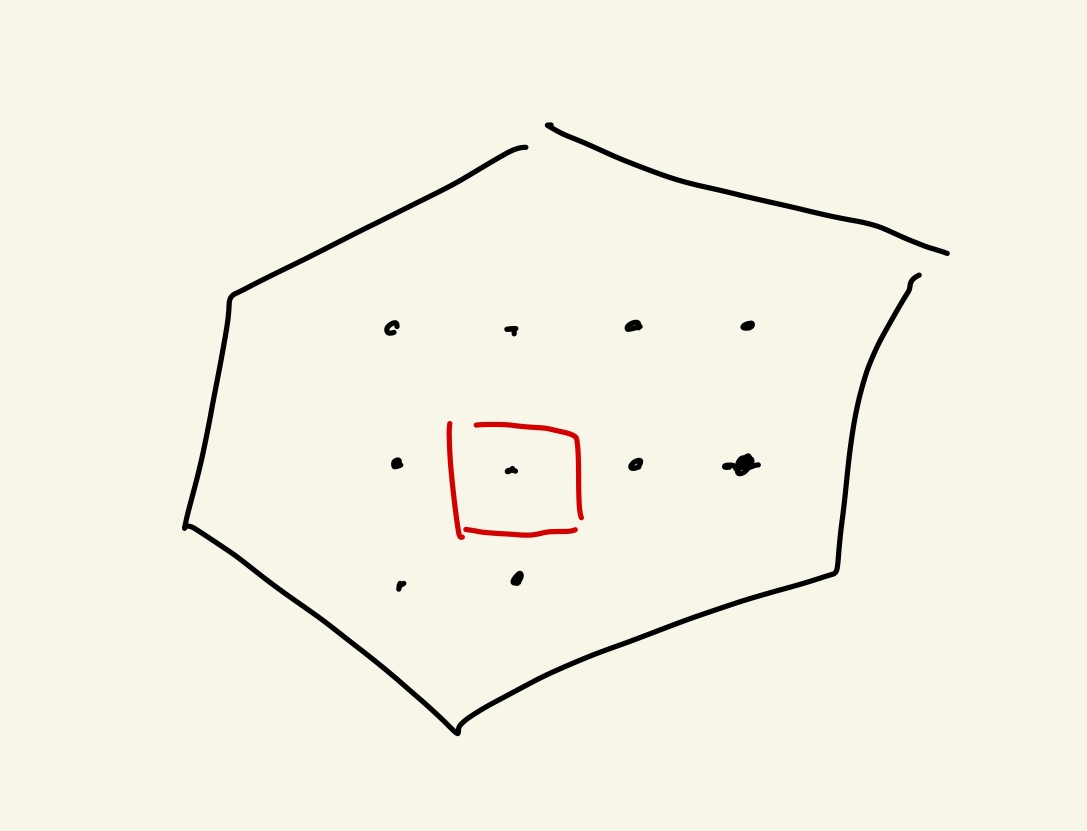
辺上の格子点は 1/2
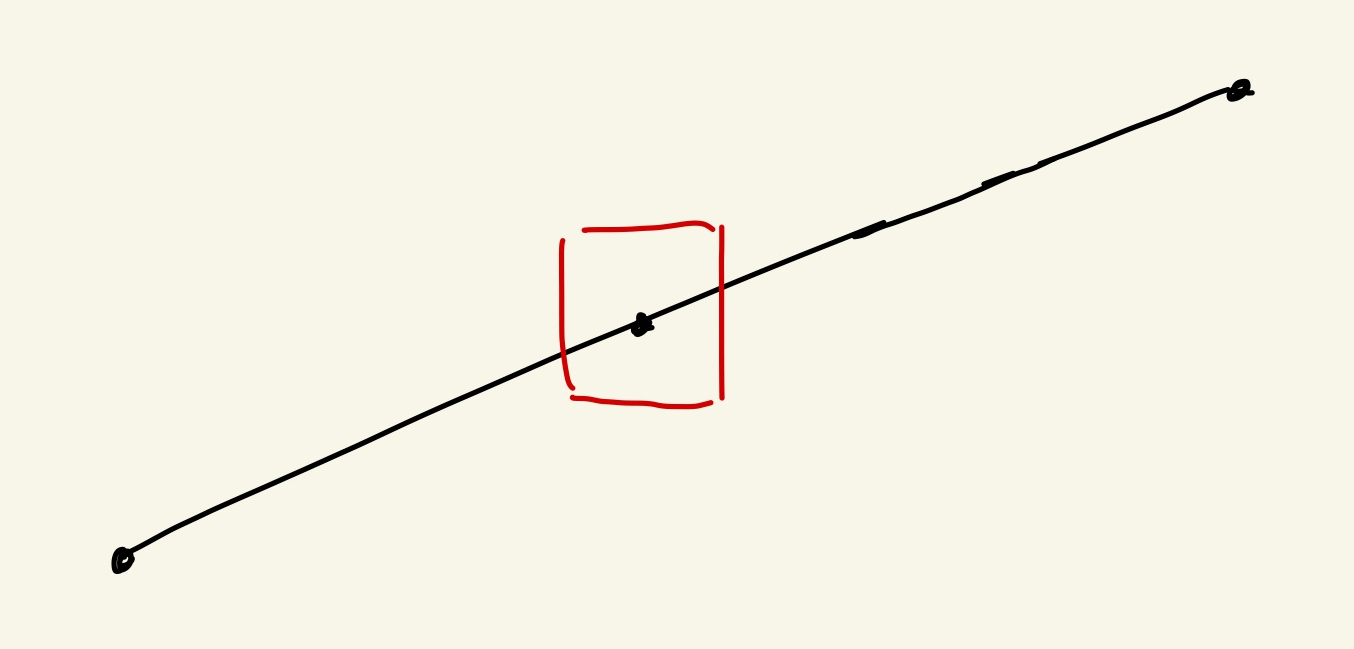
辺付近の格子点にはペアになる2つがあり、片方で足りないところをもう片方が補うので2つで貢献度1。内部にあるほうが全部負担すると考えて、この内部の点が貢献度1。
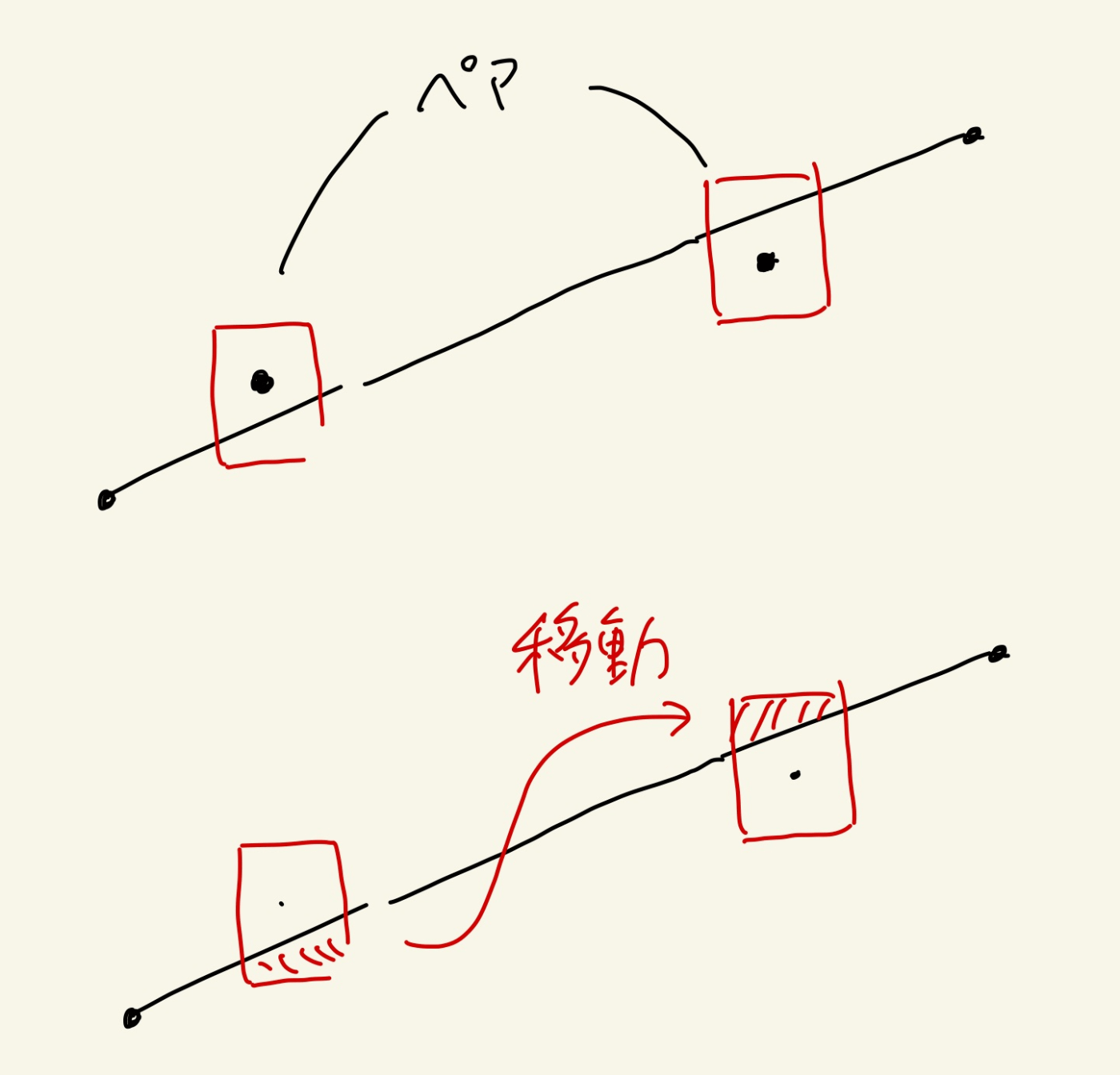
頂点(形を構成する点)は貢献度1の状態からいらないものを引いていく考え方をする。頂点数をNとする。
次のようにすると辺の両端で余計な部分が1/2あるので辺ごとに1/2減る。
辺の数と頂点の数は同じなので、頂点ごとに1/2減ると考える。

また、形を構成する点の外側に余計なものがある。
これを全部足すと正方形が出来るので1を引く。
辺上の格子点の数
先ほどと同じように最大公約数を使う
面積の決め方
2点(ax, ay)(bx, by)を結ぶラインの下の部分は
S = (bx - ax) * (by + ay) / 2
で求まる。

上のラインと下のラインを一周すると、行きと帰りで符号が反対になるので中身が求まる。
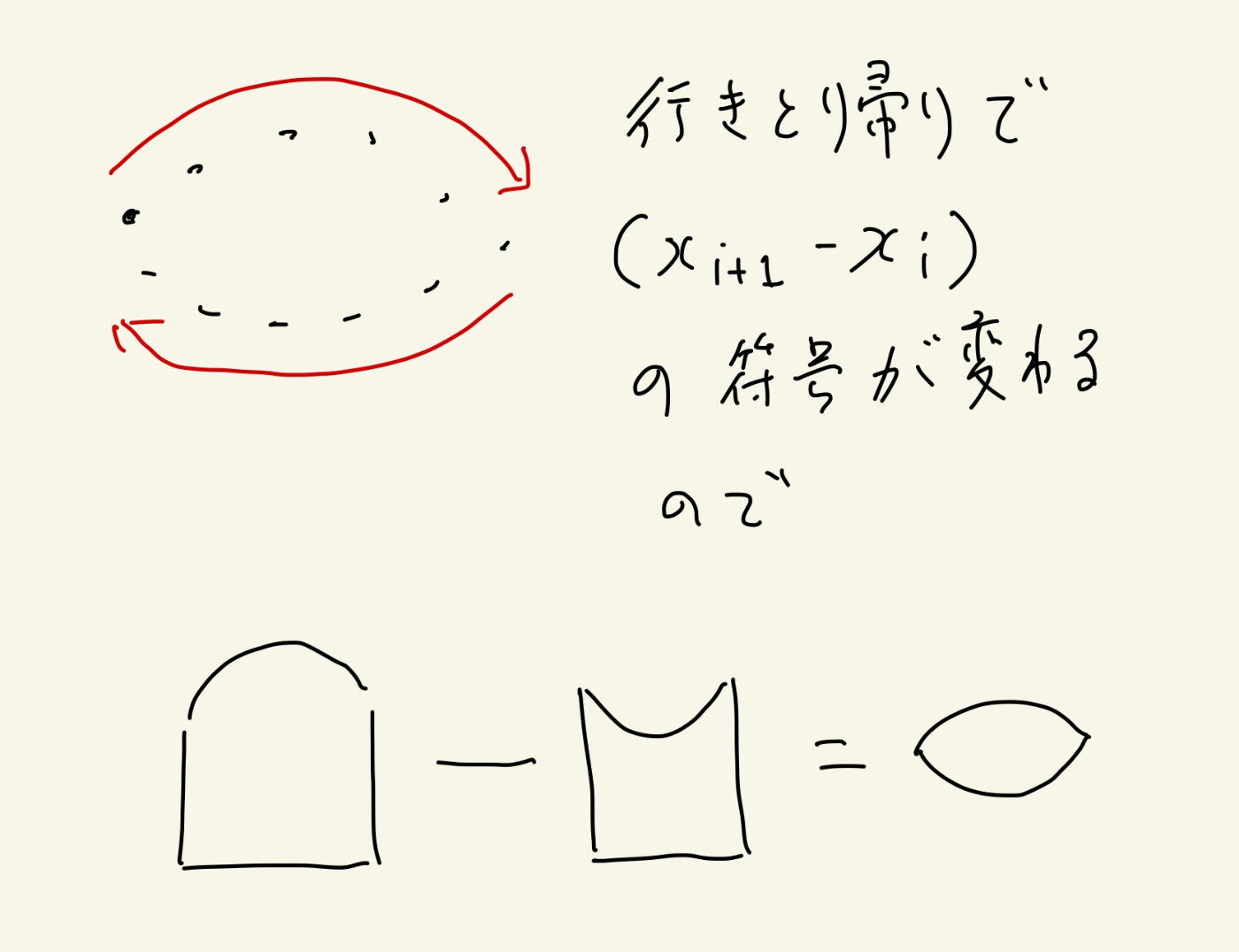
ただし、想定解法のC++のソースコードでは下ラインが往路、上ラインが復路で計算し後で絶対値を取っている。
情報がそろったら計算をする。面積Sと輪郭上の点の数bがわかっている。内部の点iとbを合わせた数を出すには
S = i + b / 2 - 1 ピックの定理 S:面積 i:内部の点 b:輪郭上の点
2S = 2i + b - 2
2S = 2i + 2b - b - 2
2i + 2b = 2S + b + 2
i + b = (2S + b + 2) / 2
Discussion