GAN, WGAN, Pix2pix, CycleGANについてまとめ

以下について順に説明.

• GANの理論
• 解決策として、Wasserstein GAN(概要)
• Pix2pix
• Cycle GAN

GANの理論

GAN（Generative Adversarial Network）は、生成器と識別器から構成される、生成モデルの一種である。
生成器は、ランダムノイズや潜在空間からの入力を使ってデータを生成する。
識別器は、生成器が生成したデータを偽物(0)、本物のデータを本物(1)と認識する様に学習する。
生成器は、識別器が騙される様なデータを生成するように学習する。

2つのニューラルネットワークを競わせてデータを学習させることから、敵対的生成ネットワークとも呼ばれる。

GANのネットワーク構造と、GANの問題点

以下に、GANのネットワーク構造を示す。(引用[1])

GANの損失関数は以下の式で表せる。

$$L = -\mathbb{E}_{x \sim p_{\text{t}}(x)}\left[\log(D(x))\right] - \mathbb{E}_{z \sim p_g(z)}\left[\log(1 - D(G(z)))\right]$$

すなわち、この損失関数を$D$に関しては最大化、$G$に関しては最小化すれば良い。
GANの損失関数の式は、期待値$\mathbb{E}$を展開し、以下のように表すこともできる。

$$L = -\int \log(D(x)) \cdot p_{\text{t}}(x) \ - \log(1 - D(G(x))) \cdot p_g(x) \,dx$$

ここで、識別器が最適化される、すなわち、$L$を$D(x)$で微分したものが0を取るような$D^*(x)$を求め、$L$に代入すると、以下の様になる。

$$L = 2JS(p_{\text{g}}| p_{\text{t}}) - 2\log(2)$$

ここで、JSdivergence は、本物と生成画像の確率分布がどれだけ離れているかを示す。このJSdivergenceを最小化することで生成器の学習を収束させることができるが、ここで以下のような問題が生じる。(引用[2])

• 勾配消失問題:生成器が最適化される時、すなわち$L$が0となる時、$JS(p_{\text{g}}\| p_{\text{t}})=0.693$となり、確率分布が一致することなく学習が止まってしまう。結果、生成器が識別器より劣り、生成されたデータの質が良くない。また、JSdivergenceは、一定距離以上離れると、値が頭打ちしてしまう。
• モード崩壊：上の問題を解決するため、生成器の損失
  
  $$-\mathbb{E}_{x \sim p_{\text{t}}(x)}\left[\log(D^*(x))\right]$$
  
  を最小化することを重視するとし、最適化された識別器の下では、以下のような式になる。
  
  $$-\mathbb{E}_{x \sim p_{\text{t}}(x)}\left[\log(D^*(x))\right]= KL(p_{\text{t}}| p_{\text{g}}) - 2JS(p_{\text{g}}| p_{\text{t}}) + 2\log(2) - \mathbb{E}_{x \sim p_{\text{t}}(x)}\left[\log(D^*(x))\right]$$
  
  $KL(p_{\text{t}}\| p_{\text{g}})$はreverse KL divergenceと言い、KL divergenceとは異なる(非対称性)。
  ここで、本物画像の分布が2つの山(モード)を持つ分布の場合、
  
  $$-\mathbb{E}_{x \sim p_{\text{t}}(x)}\left[\log(D^*(x))\right]$$
  
  を最適化すると、片方の山(モード)に偏る、または山の間で収束してしまう。前者は、似たような画像ばかり生成してしまうことが問題である。後者は、あり得ない様な画像を生成してしまう。

解決策として、Wasserstein GAN(概要)

Generative Adversarial Network）は、生成器と識別器の間にWasserstein距離（または地面距離）と呼ばれる尺度を用いて学習を行う。
GANでは、KLダイバージェンスやJSダイバージェンスを使用して分布の違いを計測していた。
Wasserstein距離は、確率分布の間の距離で、最適輸送問題とも呼ばれる。これは、ある地点から別の地点への荷物の輸送コストを最適にする問題で、確率分布間の距離を定義することができる。
元は、ある土の山を他の山に移動させる最短距離(最小コスト)を求める手法であることから、EM(Earth Moving)距離とも呼ばれている。WGANでは、生成画像の確率分布を本物画像の確率分布に近づける最短距離を求める。式では、以下の様な形をとる。

$$W(p _ r, p _ g) = \inf_{\gamma\sim\Pi(p _ r, p _ g)}\mathbb{E} _ {(x,y) \sim\gamma}\left[ ||x - y ||\right]$$

すなわち、生成画像の確率分布のある地点xと本物画像の確率分布のある地点yの距離x-yの期待値(加重平均)の下限を示す。
$\gamma(x, y)$は同時確率、$\Pi(p _ r, p _ g)$は周辺分布確率である。
ここで、下限はコンピュータの計算上扱いにくい(計算不可能)ので、上式がk-リプシッツ連続であるという条件をつけることで、以下の式となる。

$$L(p _ {r}, p _ {g}) = W(p _ {r}, p _ {g}) = \max _ {w \in W} \mathbb{E} _ {x \sim p _ {r}} [f _ {w}(x)] - \mathbb{E} _ {z \sim p _ {z}} [f _ {w}(g _ {\theta}(z))]$$

ここで、$f$は、識別器、$g$は生成器の関数に対応する。
この損失関数を最小化することを目標とする。
$w$の範囲を制限するクリッピングをすることで、k-リプシッツ連続性を維持している。



Wasserstein distanceが優れているのは、以下の点である。
本物画像と生成画像の確率分布を同じ一様分布[0,1]とし、これらの距離を計算するとする。JS divergenceは2つの確率密度が重ならない場合、どの距離においても$log2$となる。重なると急に0となり、離散的である。つまり、微分不可能である。対して、Wasserstein distanceは確率密度が重ならない場合と重なる時で連続的な関数であり、勾配降下法で学習する場合に安定すると考えられる。これにより、生成器と識別器の学習バランスをとり、勾配消失やモード崩壊を防いでいる。

Wasserstaein距離以外の最適輸送アルゴリズム

Wasserstaein距離以外に、Sinkhorn-Knopp距離と呼ばれるものがある。
Sinkhorn-Knoppは、最適輸送問題を解くために使用されるアルゴリズムの一つ。
最適輸送問題における目的関数をエントロピー正則化し、Sinkhorn-Knopp アルゴリズム最小輸送コストを求めることができる。
Sinkhorn-Knopp距離は、ドメイン適応やスタイル変換などのタスクに用いられる。

Pix2pix

Pix2pixのネットワーク構造

以下に、Pix2pixのネットワーク構造を示す。(引用[3])

Pix2pixは、ドメイン変換を行うためのGANモデル。ドメイン変換とは、馬の画像をシマウマの画像に変換するなどの画像変換をすることである。2017年に公開された。
訓練データとして、入力画像とそれに対応する出力画像のペアを使用して学習させることで、ある入力画像から、異なる画像を生成することができる。
CGAN(条件付きGAN)の構造を用いている。
CGANは、入力ノイズと本物画像にラベル情報を加えることで、指定したラベルの画像を生成できるようにしたGAN。
Pix2pixでは、ラベルの代わりに画像を用いている。
生成器のモデルにはUNetを採用し、指定画像(CGANで言うラベル)を入力としている。各層にDropoutを加えることで、ノイズを加えている。
識別器では、PatchGANと呼ばれる、識別画像をパッチに分解し、パッチ毎に識別を行う手法を用いている。出力は、全パッチの真偽(1,0)の平均、つまり正解率となる。



Pix2pixの損失関数は以下の様になる。

$$L = \mathbb{E}_{x \sim p_{\text{t}}(x)}\left[\log(D(x, y))\right] - \mathbb{E}_{z \sim p_g(z)}\left[\log(1 - D(x, G(z)))\right] + ||y - G(x, z)||_{1}$$

ここで、第一,二項はCGANの損失関数、第三項はL1ノルム、つまり、本物と生成画像のピクセル間距離である。CGANでは、入力xの時のy,G(z)を識別器、生成機にそれぞれ入力している。つまり、条件付き確率である。
上に述べたように、第一,二項では、PatchGANにより、細かい部分の損失を見るようにしている。
第三項では、大まかな部分の損失を見るようにすることで、生成画像の品質向上を行う。

Pix2pixの問題点

ピクセル分布が同じような画像のペアを必要とするため、データセットの作成にコストがかかる。

Cycle GAN

CycleGANは、ドメイン間の画像変換を行うためのGANモデル。
Pix2pixと異なり、画像のペアが無くてもドメイン変換を行うことができる。
2つの生成器と2つの識別器から構成され、一つのドメインに対して1つの生成器と1つの識別器から構成される。
識別器は、FCNを用いており、この点ではDCGANの構造と似ている。

CycleGANのネットワーク構造

以下に、CycleGANの学習サイクルを示す。(引用[4])

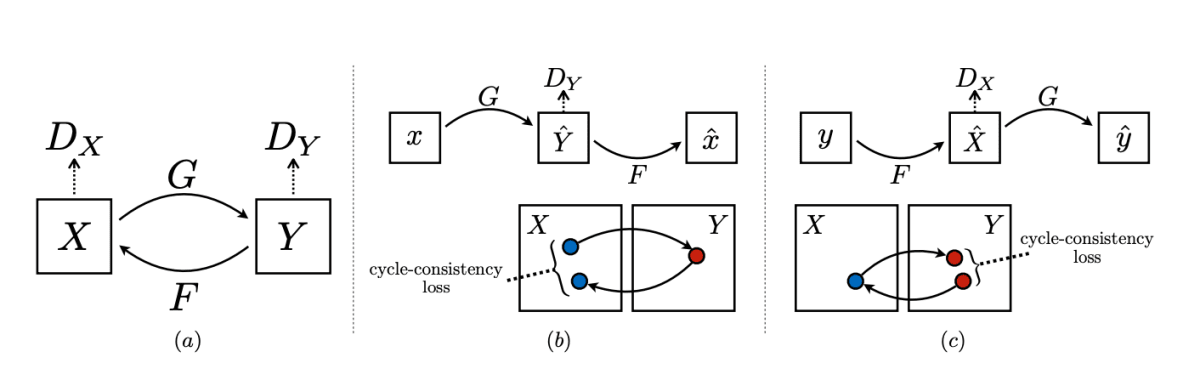
損失関数は、以下の式で表せる。

$$L_{\text{CycleGAN}} = L_{\text{Cycle}}(G, F, X, Y) + L_{\text{Gan}}(G, D_Y, X, Y) + L_{\text{Identity}}(G, F, X, Y)$$

すなわち、Cycle Consistency LossとAdversarial, Loss Identity lossから成る。
Cycle Consistency Loss(サイクル一貫性損失)は、入力画像を変換し、さらにその変換後の画像を逆変換して元の画像を再生成し、変換前の画像と一致するように学習し、以下の式で表せる。

$$L_{\text{Cycle}}(G, F, X, Y) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[|| F(G(x)) - x ||]+\mathbb{E}_{y \sim p_{\text{data}}(y)}[||G(F(y)) - y||]$$

Adversarial Loss (敵対性損失)は、生成イメージの分布とターゲットの分布を一致させるために用いられ、以下の式で表せる。

$$L_{\text{Gan}}(G, D_Y, X, Y) = \mathbb{E}_{y \sim p_{\text{data}}(y)}[\log D_Y(y)] + \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log(1 - D_Y(G(x)))]$$

Identity loss(恒等損失)は、同じ側のドメインの画像を入力したとき、出力が入力と同じドメインの画像を出力するようにする。以下の式で表せる。

$$L_{\text{Identity}}(G, F, X, Y) = \mathbb{E}_{y \sim p_{\text{data}}(y)}[|| F(y) - y ||] + \mathbb{E}_{x \sim p_{\text{data}}(x)}[|| G(x) - x ||]$$

Identity lossにより、色構成の品質が向上する。
これらを、2つのドメインに対して行うので、3×2個の損失を計算する。
また、Batch normalizationの代わりにInstance normalizationを採用している。
CycleGANは、data augmentationの手段としても用いられている。

参考文献

[1] Zhengwei Wang, Qi She, and Tomas E. Ward. Generative adversarial networks in computer vision:
A survey and taxonomy, 2020.
[2] Martin Arjovsky, Soumith Chintala, and L ́eon Bottou. Wasserstein gan, 2017.
[3] Kanishk, Tanishk Nandal, Prince Tyagi, and Raj Kumar Singh. Generation and parameterization of
forced isotropic turbulent flow using autoencoders and generative adversarial networks. In Volume
10: Fluids Engineering. American Society of Mechanical Engineers, nov 2021.
[4] Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A. Efros. Unpaired image-to-image transla-
tion using cycle-consistent adversarial networks, 2020.