📈

Rustでフーリエ変換(DTFT)

2022/01/06に公開

Rust

FFT

tech

モチベーション

音声技術の勉強として、どシンプルな離散フーリエ変換(DTFT)を実装。
高速化(FFT)は未考慮。FFTの記事も別に書く予定。 (→ こちらに書きました)

概要

この記事では「フーリエ変換 = 時系列データ(x) -> 周波数(f[Hz]) の変換」とする。

\begin{array}{cc} X_f = \displaystyle\sum_{k=0}^{N-1}x_ke^{-i{\omega}t} & \omega = 2{\pi}f & t = k / fs \end{array}

$X_f$ : 周波数 $f$ [Hz]におけるフーリエ変換結果
$f$ : 周波数[Hz]
$N$ : 入力フレームの個数
$x_k$ : 各入力フレームの値[bit]
$\omega$ : 角周波数
= 1秒間に進む角度(ω=2πで1周)
$t$ : 各入力フレーム時点での再生時間[s]
$f_s$ : サンプリング周波数[Hz]
= 1秒間に収録されるフレーム数

補足

フーリエ変換の説明は省略 (詳しくはこちら)

端的に説明するなら「 $e^{-i{\omega}t}= cos({\omega}t) - isin({\omega}t)$ なので、 $x_k$ が周波数 $f$ のsin波,cos波に近い値を持っているほど $X_f$ の絶対値は大きくなりスペクトラムとして表れる」ということです。

実務では入力データがキレイなsin波,cos波でないことも多いため、「窓関数」でスペクトラムに表れやすく加工しているそうです (詳しくはこちら)

実装

結果データのサイズは、ナイキスト周波数(= $f_s/2$ )とする
- 折り返し波による競合を防ぐため (詳しくはこちら)
高速化への考慮ゼロ

src/main.rs

use num::complex::Complex;
use std::f64::consts::PI;

pub fn dtft(frames: Vec<f64>, fs: i64) -> Vec<Complex<f64>> {
    let mut rslt: Vec<Complex<f64>> = Vec::new();
    // 1 <= f <= fs/2
    for f in 1..=(fs / 2) {
        let mut sigma: Complex<f64> = Complex::new(0.0, 0.0);
        // 0 <= k <= N-1
        for (k, xk) in frames.iter().enumerate() {
            // t = k / fs
            let t: f64 = (k as f64) / (fs as f64);
            // ω = 2πf
            let w = 2.0 * PI * (f as f64);
            // e^(-iωt)
            let exp = Complex::new(0.0, -w * t).exp();
            // X(f) = ∑xk*e^(-iωt)
            sigma += xk * exp;
        }
        rslt.push(sigma);
    }
    return rslt;
}

検証

以下を実行して、期待通りhz(=2000)で最大値になればOK。

src/main.rs

// --snip--

fn main() {
    // create sin_curve frames
    let flame_len = 1000;
    let samplerate = 16000;
    let hz = 2000;
    let sin_curve: Vec<f64> = (0..flame_len)
        .map(|a| (a as f64) * 2.0 * PI * (hz as f64) / (samplerate as f64))
        .map(|a| a.sin())
        .collect();

    let rslt = dtft(sin_curve, samplerate);

    let (max_index, max) =
        rslt.iter()
            .enumerate()
            .fold((usize::MIN, f64::MIN), |(i_a, a), (i_b, &b)| {
                if b.norm() > a {
                    (i_b, b.norm())
                } else {
                    (i_a, a)
                }
            });
    println!("rslt len: {:?}", rslt.len()); // = fs/2
    println!("max rslt f: {:?}", max_index + 1); // 1 <= f <= fs/2
    println!("max rslt: {:?}", max);
}

成功例👌

xx % time cargo run
   Compiling fft_rs v0.1.0 (/Users/xx)
    Finished dev [unoptimized + debuginfo] target(s) in 0.49s
     Running `target/debug/xx`
rslt len: 8000
max rslt f: 2000
max rslt: 499.99999999999994
cargo run  0.89s user 0.16s system 68% cpu 1.527 total

補足

flame_lenを増やせば(高速化していないので遅くなりますが) max rsltの値がどんどん大きくなります。

↓イメージ

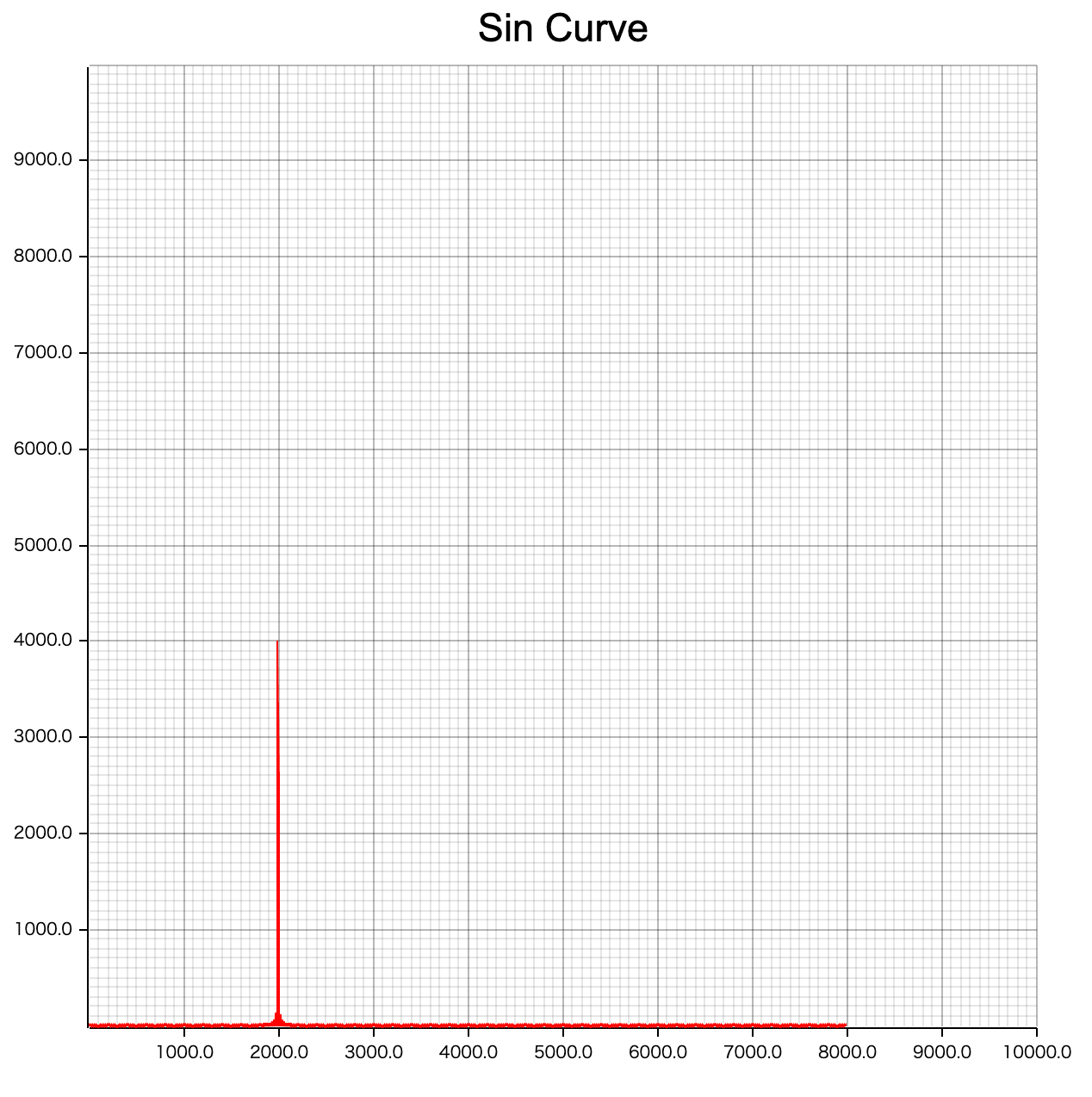
高速化も含めた実装記事も書きました。

それでは。

モチベーション

概要

実装

検証

補足

Discussion