集合関数のベイズ最適化
概要
この記事では、有限集合
集合関数のブラックボックス最適化にはいくつかの研究がありますが、この記事では以下の論文で提案されている手法を紹介します。
また、この論文の手法は集合のサイズが一定の場合を対象としていますが、この記事では集合のサイズも可変とした場合の最適化方法についても検討します。
なお、この記事ではガウス過程・ベイズ最適化の基本的な知識を前提としています。
集合のサイズが一定の場合
まずは集合のサイズが一定の場合を考えます。この場合は以下のように定式化できます。
集合のカーネル関数
ベイズ最適化では目的関数をガウス過程でモデル化することが一般的です。今回の問題でも関数
ガウス過程でモデル化する際にはカーネル関数が必要です。集合関数をガウス過程で表現するためには、集合を対象とするカーネル関数が必要です。
集合のカーネル関数の必要性
集合のカーネル関数が必要な理由を考えてみます。もしRBFカーネルのような一般的なカーネルで十分であれば、わざわざ集合用のカーネルを考える必要はありません。
ガウス過程ではカーネル関数を用いて入力間の類似度を測り、類似度に基づいて予測します。類似度の高い入力は予測値も似た値になるという考え方です。そのためカーネル関数が入力間の類似度を適切に表現できる必要があります。
例えば
そのため集合の類似度を適切に表現するためのカーネル関数が必要です。
Deep Embeddingカーネル
上記論文では集合のカーネル関数としてDeep Embeddingカーネルを提案しています。
集合の要素に対する正定値カーネル
ここで、
例: 施設配置問題 (p-メディアン問題)
p-メディアン問題を例にとり上記のカーネルを用いたベイズ最適化を適用してみます。
コードはこちらのノートブックにあります。
問題設定
p-メディアン問題とは以下のような問題です。
- 施設を配置する候補地点の集合
X C - 各顧客
c \in C f \in X d_{cf} -
X p - 各顧客は最も近い施設にサービスを受けに行きます。
- サービスを受けるために顧客が移動する距離の総和が最小になるような施設の開設地点を求めたいです。
この問題は以下のように定式化できます。
今回は以下のようなランダムな入力を用意しました。
-
C [0, 1]^2 -
X = C -
d_{ij} -
p = 5
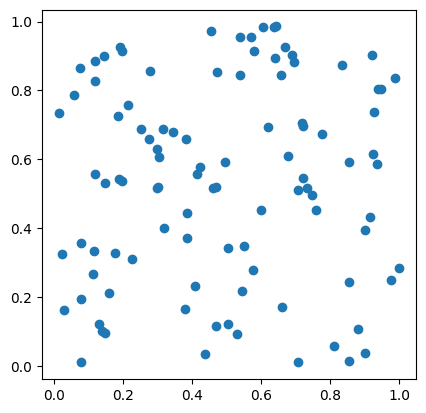
顧客集合
アルゴリズムの設定
ベイズ最適化アルゴリズムの設定は以下の通りです。
アルゴリズムの設定
-
カーネルの設定
- 上で説明したDeep Embeddingカーネルを使用。
-
k_X -
k_H(d)=\sigma^2\exp(d^2/\theta) - カーネルのハイパーパラメータは周辺尤度最大化で決定。
-
初期訓練データ
- ランダムにサンプリングした5点のデータを使用。
-
最適化のステップ数
- 100ステップ。
-
獲得関数
- 対数期待改善量(LogEI)を使用。
- 空集合から要素を追加するビームサーチで獲得関数を最適化。ビーム幅は5。
結果
以下はベイズ最適化の進行状況を示すグラフです。各ステップでの目的関数値の変化を最適値に対する比率で表示しています。また、比較のためにランダム探索の結果も示しています。
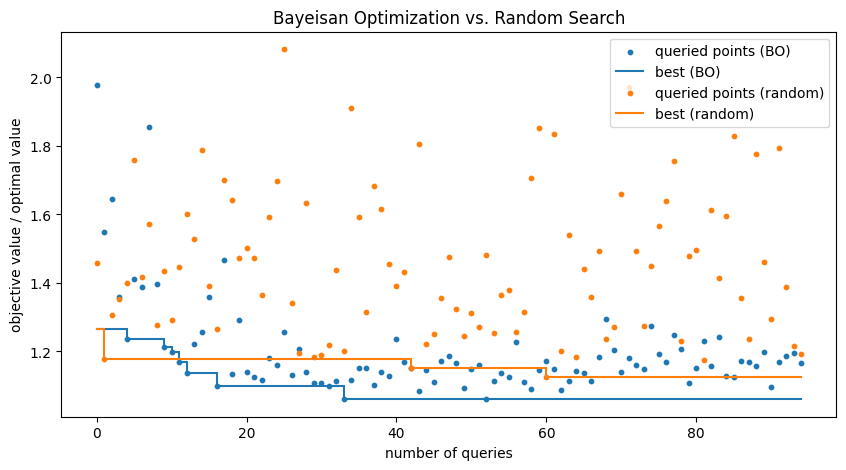
最適化の過程。横軸はステップ数、縦軸は目的関数値の最適値に対する比率。青点はベイズ最適化の各ステップで評価された目的関数値、青線は各ステップまでの最良の目的関数値。オレンジ点はランダム探索の結果、オレンジ線はランダム探索の最良値。
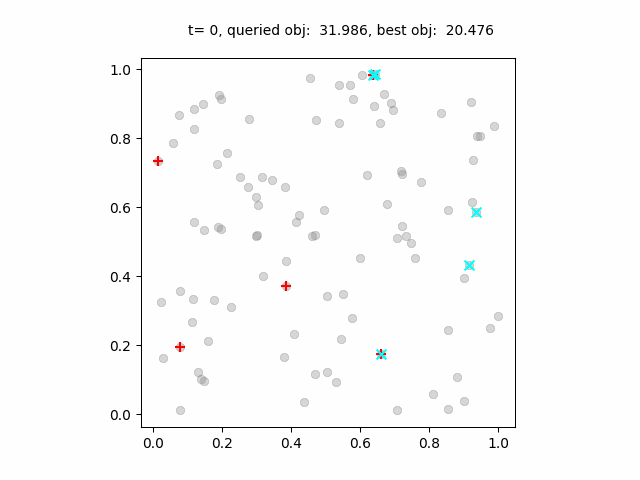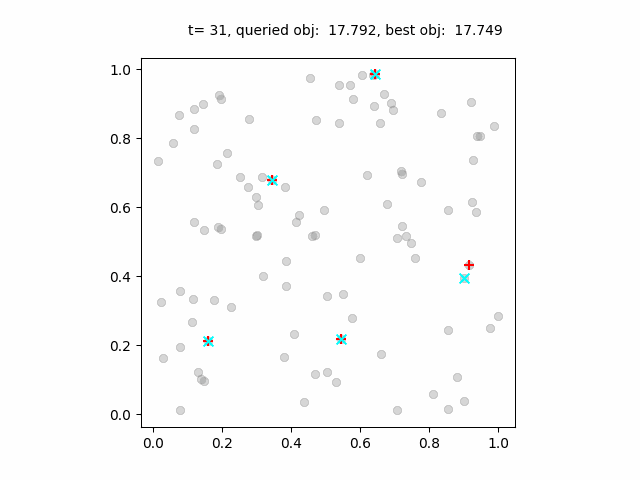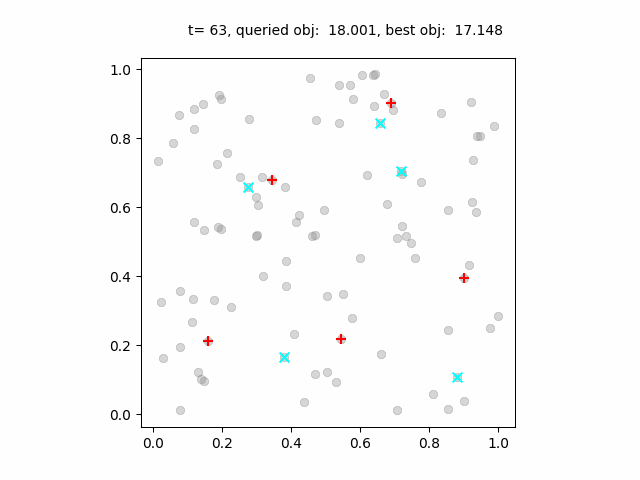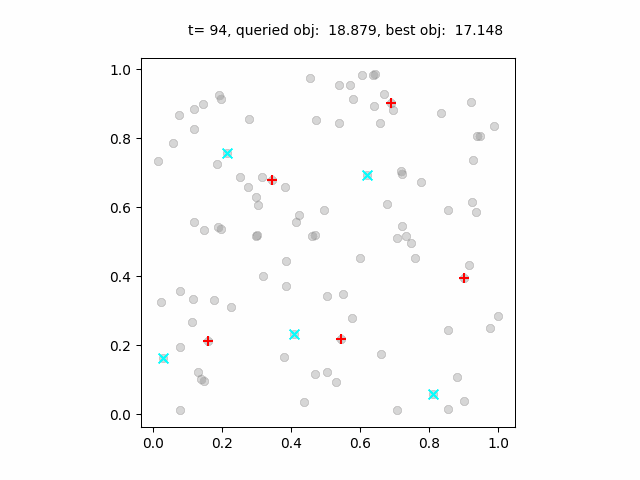
ベイズ最適化の過程のアニメーション。青点は各ステップで試行された施設の位置、赤点は最良の施設配置。
ベイズ最適化はランダム探索よりも早く良い解に収束していますが、最適解とは数%の差があります。
以下はベイズ最適化で得られた最良の施設配置と、最適解の施設配置です。ベイズ最適化の結果は適度に散らばっており妥当な結果に見えます。ただ、最適解と比べると若干の差があります。
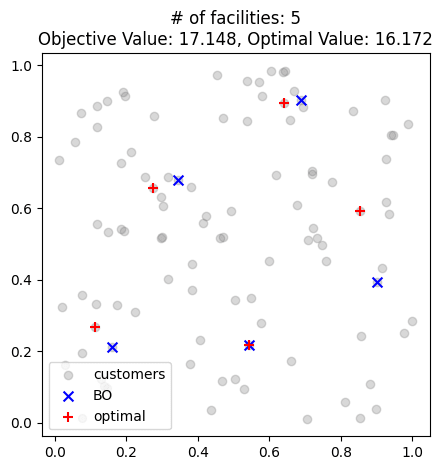
最終的な施設配置。青点はベイズ最適化の最終的な施設配置。赤点は最適解。
集合のサイズが可変の場合
上では集合のサイズが固定の場合を考えましたが、次に集合のサイズが可変の場合を考えます。
Deep Embedding カーネルの問題点
Deep Embeddingカーネルは集合の要素に関して平均を取るため、サイズが大きく異なる集合同士でも類似度が高くなる可能性があります。これは施設配置問題のように施設数(=集合のサイズ)が多いほど目的関数値が小さくなる場合などには問題です。施設数(=集合のサイズ)の違いを考慮する必要があります。
Deep Embedding カーネルの拡張
この問題に対処するため、以下のようにカーネル
ここで、
このカーネル
集合のサイズと目的関数値の多目的ベイズ最適化
集合のサイズを可変にして単純に目的関数が良くなる集合を見つけるのであれば上のカーネル
しかし、単純に目的関数が良い集合を見つけたいのではなく、様々なサイズの場合に対して良い集合を見つけたい場合があります。
例えば上で扱った施設配置問題(p-メディアン問題)では施設数を増やすほど目的関数値は小さくなります。また、目的関数では考慮していませんが通常は施設数は増やすほど開設のコストが増えるため、施設数は少ない方が良いです。そのため施設数と目的関数値のトレードオフを考慮した最適化を行いたいことがあります。
このように目的関数と集合のサイズのトレードオフ関係を考慮して最適化する方法として多目的最適化が考えられます。別の方法として
ベイズ最適化で多目的最適化を行うアルゴリズムは様々ありますが、例えば期待超改善量を最大化するように次に試行する集合を選択する方法などがあります。
例: 施設配置問題 (p-メディアン問題)
上で扱った施設配置問題(p-メディアン問題)を再び例に取り上げます。問題設定は同じですが、今回は目的関数値と施設数の両方を考慮して最適化を行います。具体的な違いは以下の通りです。
- 施設数
p 3, 4, 5, 6, 7 - 期待超改善量を獲得関数として使用する。
ソースコードはこちらのノートブックにあります。
結果
以下はベイズ最適化の進行状況を示すグラフです。各施設数において目的関数が減少しており最適化が進んでいることがわかります。
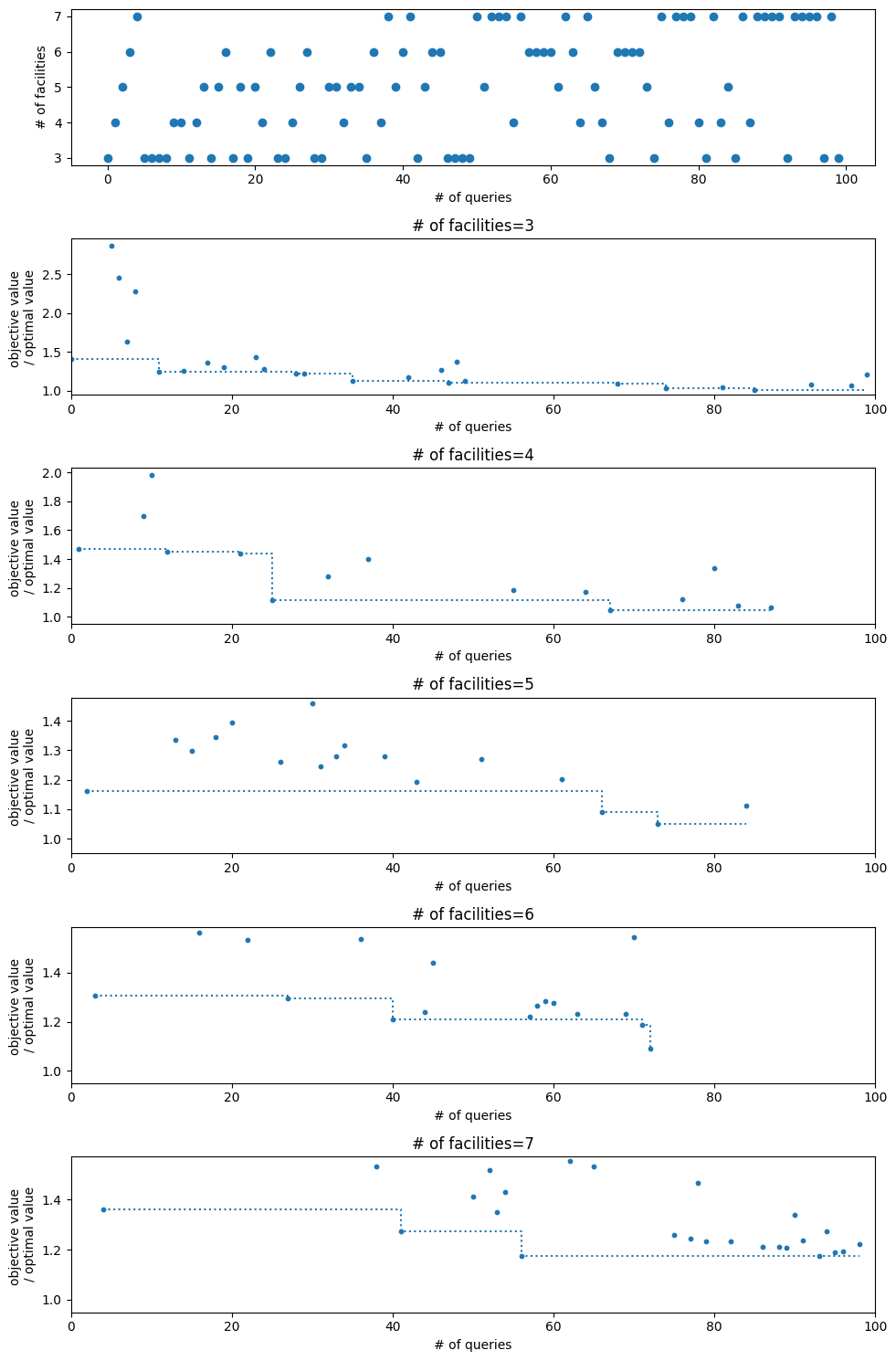
ベイズ最適化の過程。最上段は各ステップで試行された施設数を示しています。2段目以降は各施設数ごとの最適化の進行状況です。2段目以降の縦軸は目的関数値の最適値に対する比率です。点が各ステップにおける結果で、点線はそのステップまでの最良の結果です。
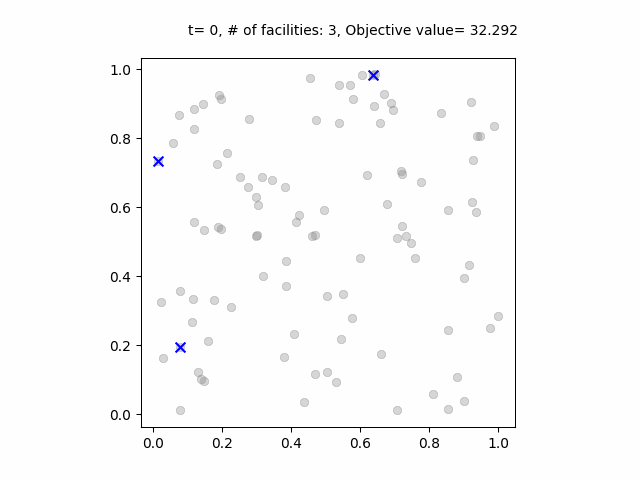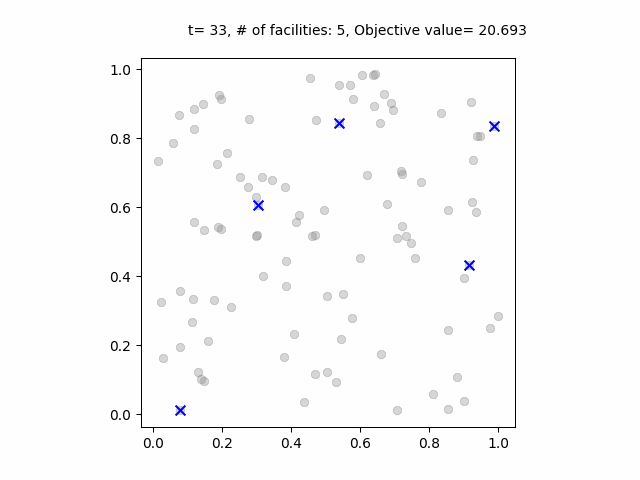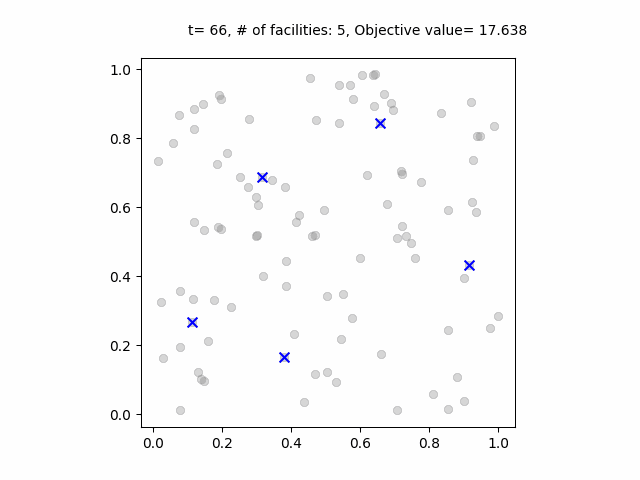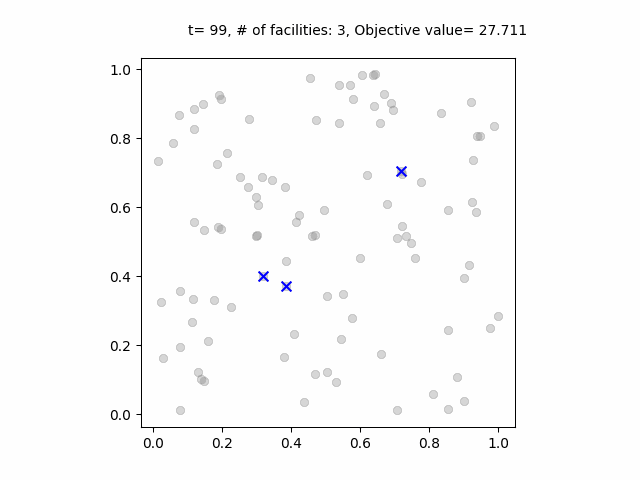
ベイズ最適化の過程のアニメーション。青点は各ステップで試行された施設の位置。
以下は施設数に対する目的関数値のグラフです。施設数が多くなるほど目的関数値が小さくなることが確認できます。
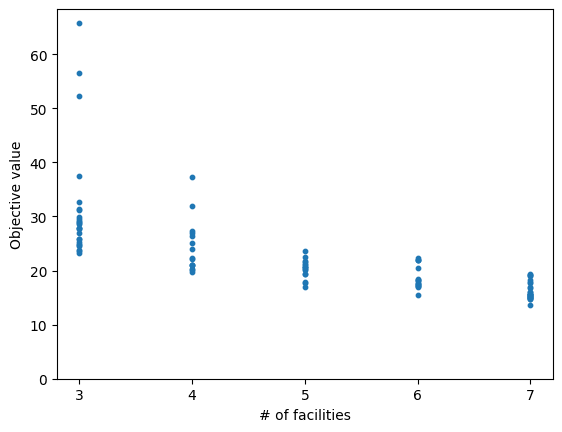
施設数と目的関数値の散布図
以下は施設数ごとのベイズ最適化の最終的な施設配置と最適解の配置です。ベイズ最適化の解は適度に散らばっており妥当な解に見えますが、最適解とは差があることもわかります。
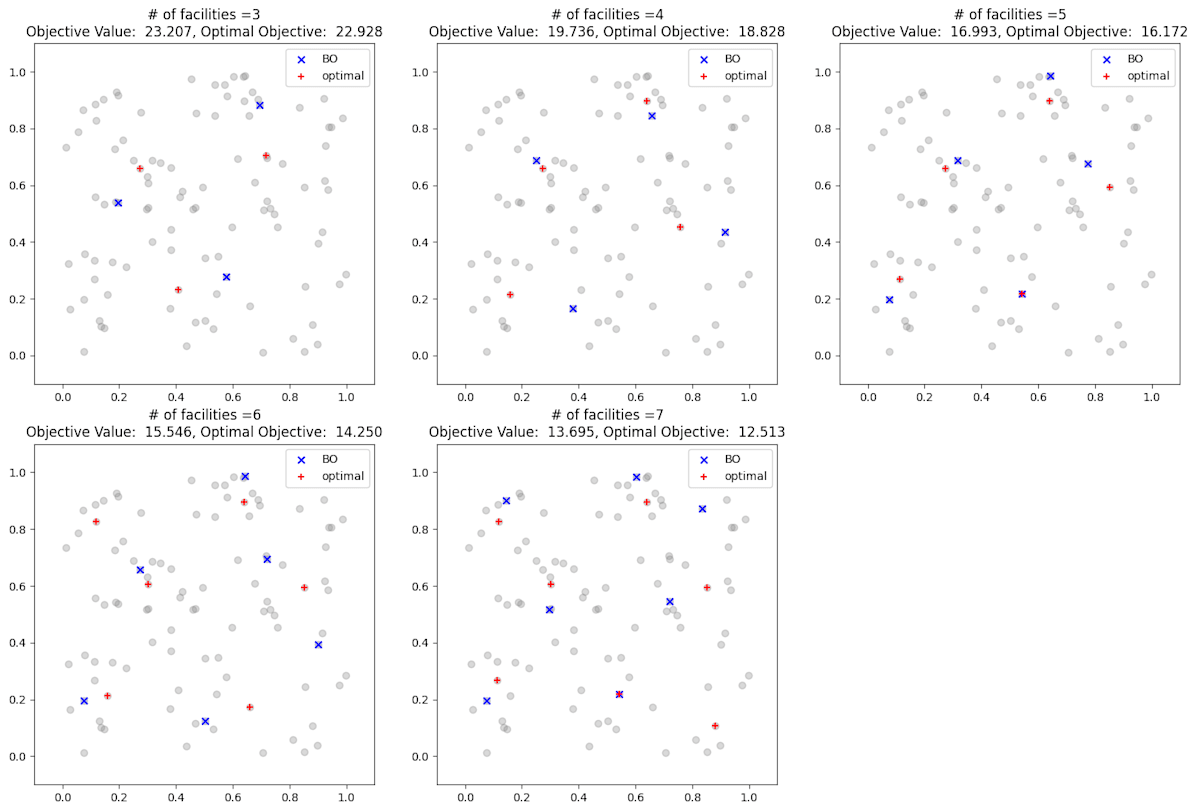
施設数ごとの最終的な施設配置。青点はベイズ最適化の最終的な施設配置。赤点は最適解。
他の方法との比較
簡単ですが他の手法との比較も行います。以下の手法を比較してみます。
| 名称 | カーネル | 説明 |
|---|---|---|
| Random | ランダムに集合のサイズ |
|
| EI (indep) |
|
|
| EI (rotate) |
|
|
| EI | 各pごとに期待改善量が最大となる集合を探索したのちに、最も期待改善量が大きな |
|
| EHVI | 上に述べた多目的ベイズ最適化による方法。 |
問題設定は上と同様ですが乱数の種を変えてそれぞれ10回繰り返して比較します。
以下のグラフでは 100 ステップが終了した時点の最良の目的関数値の最適値に対する比率を施設数ごとに比較しています。上に述べた多目的ベイズ最適化(EHVI)が最も良い結果を出していることがわかります。
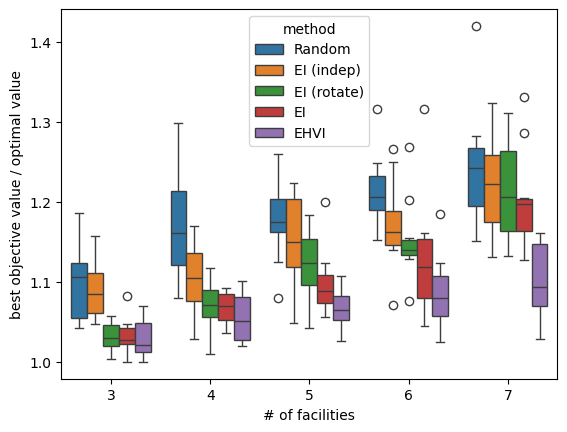
他の手法との比較の箱ひげ図
コードはこちらのノートブックにあります。
まとめ
この記事では、集合関数のベイズ最適化について、集合のサイズが一定の場合と可変の場合の最適化手法を紹介しました。
集合のサイズが一定の場合には、Deep Embeddingカーネルを用いたベイズ最適化手法を紹介し、施設配置問題を例に実験して良好な結果を得ました。
また、集合のサイズが可変の場合のためにサイズの違いを考慮したカーネル関数を導入しました。また、集合のサイズと目的関数との間にトレードオフ関係がある場合に対して多目的ベイズ最適化による方法を紹介しました。こちらも施設配置問題を例に実験して良好な結果が得られました。
-
2^X X -
このような設定なのでk-medoidクラスタリングの問題ともいえます。 ↩︎
-
集合のサイズが異なる場合を別のタスクと考えたマルチタスクカーネルといえます。 ↩︎

Discussion