ソフトウェアテスト技法
ブラックボックステスト
プログラムの中身がどうなっているかは考慮せず、インプットとアウトプットのみに着目するテスト
ホワイトボックステスト
プログラムの中身に着目して、プログラム内のそれぞれの処理が正しく動くかを確認するテスト
同値分割法
ブラックボックステストで使用されるテスト技法の一つ。
入力値により同じ処理をするグループに分割し、グループ内で代表的な入力値を選択しテストする技法。
同値分割した各グループのことを「同値クラス」という。
| 入力 | テストケース | 出力 |
|---|---|---|
| 39以下 | 20 | エラーメッセージ |
| 40-99 | 60 | 無料 |
| 100-140 | 120 | 1500円 |
| 141-200 | 170 | 3000円 |
| 201以上 | 205 | エラーメッセージ |
- メリット:テストケースを著しく減らし、時間を節約できる
- デメリット:各同値クラスで中間の値をテストした場合、境界値でバグが発生する可能性がある
境界値分析
ブラックボックステストで使用されるテスト技法の一つ。
境界値(同値クラスの端)とその前後の値に対してテストする技法。
基本的に、テストケースは以下の規則に沿って選択される。
- 境界値の1つ下
- 最小の境界値
- 最大の境界値
- 境界値の1つ上
【例】
バスのチケット料金システム
下記以外の場合、エラーが発生する
| 年齢 | 料金 |
|---|---|
| 0~5才 | 無料 |
| 6~19才 | 800円 |
| 20~60才 | 1000円 |
| 61~120才 | 800円 |
上記の場合、テストケースは下記のようになる。
| テストケース | 期待値 |
|---|---|
| -1才を入力する | エラーが発生すること |
| 0才を入力する | 料金=無料 |
| 5才を入力する | 料金=無料 |
| 6才を入力する | 料金=800円 |
| 19才を入力する | 料金=800円 |
| 20才を入力する | 料金=1000円 |
| 60才を入力する | 料金=1000円 |
| 61才を入力する | 料金=800円 |
| 120才を入力する | 料金=800円 |
| 121才を入力する | エラーが発生すること |
- メリット:効率的に境界値のバグを見つけることができる
- デメリット:複数の入力値に対して複雑に出力仕様が違うようなシステムのテストでは、使用しにくい場合がある
(その場合はデシジョンテーブルがよい)
デシジョンテーブル(決定表)
ブラックボックステストで使用されるテスト技法の一つ。
対象が取り得る条件(入力)と、その結果の動作(出力)を洗い出した上で整理し、マトリクス上に一覧化した表のこと。
【例】
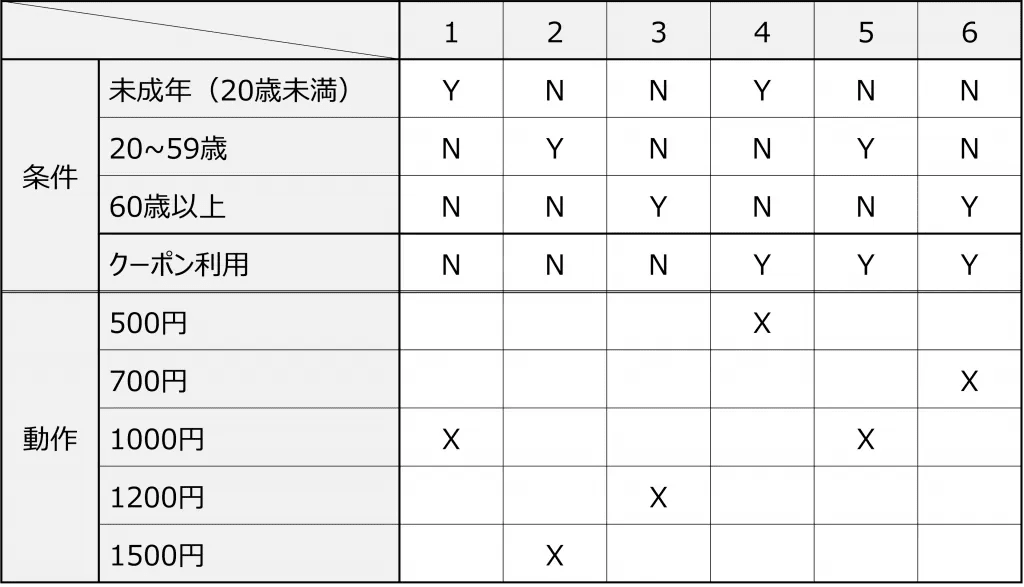
※ 引用元
デシジョンテーブルの書き方
-
条件が何かを特定して記述する

-
動作が何かを特定して記述する

-
条件の組み合わせをすべて指定する

-
条件の組み合わせに対応する動作をすべて指定する
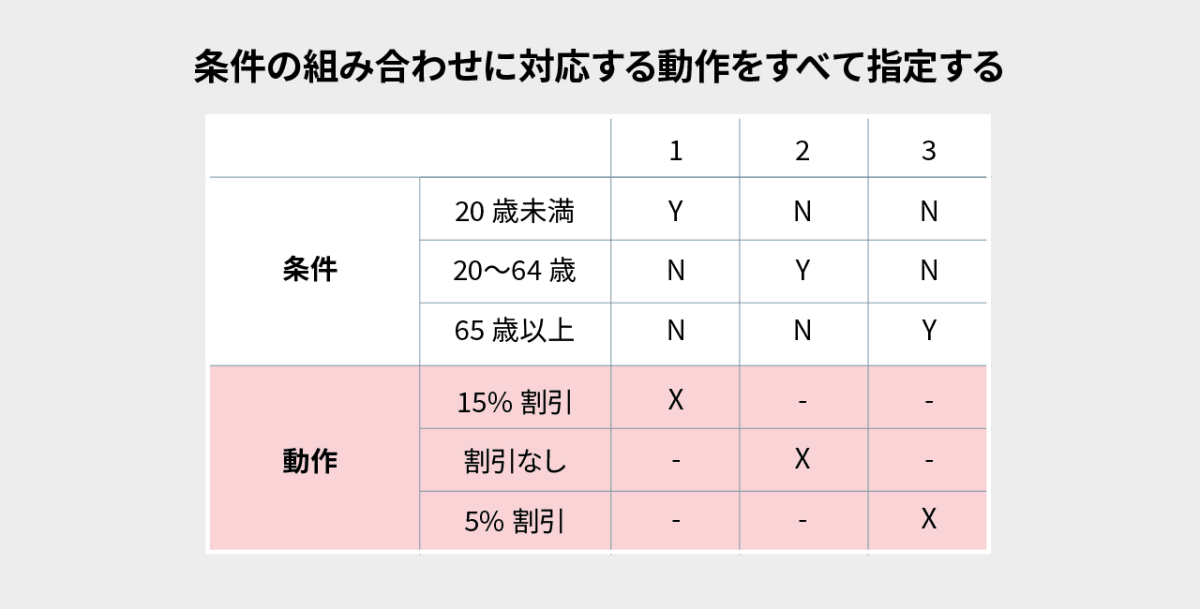
※ 引用元
- メリット:
- 複雑な条件や複数の条件の組み合わせを整理することができる
- 網羅性を可視化し抜け漏れがないか確認できる
- 矛盾している条件の組み合わせを特定することができる
- 可視化されているので他者にもわかりやすい
- すべてのテストレベルに適用できる
- デメリット:
- 複雑な条件や複数の条件の組み合わせが増えるとテストケースが増加する
- 複雑な条件や複数の条件の組み合わせが多いと作成に時間がかかる
状態遷移テスト
状態遷移モデルをもとにして、そのモデルを網羅する遷移パスをテストする。
網羅する基準のことをカバレッジアイテムといい、状態、遷移、Nスイッチなどがある。
状態が遷移するパスだけでなく、状態が遷移しないこともテストする。
0スイッチカバレッジ
テストケースで全イベントを網羅すること。
状態遷移テストにまとめた全イベント・状態に対してテストが行われる。
1スイッチカバレッジ
0スイッチカバレッジの上位にあたる基準。
2回のイベントで遷移する3つの状態をすべて網羅するようテストケースを作成する。
C1カバレッジ
全ての判定条件の真偽が少なくとも一回実行されるようなテストを実施する。
状態遷移表のセル一つひとつに対してテストケースを作成すれば良い(?)
0スイッチカバレッジとC1カバレッジの違い
C1カバレッジでは各分岐ポイントで両方の分岐がテストされる必要があるが、0スイッチカバレッジは特定の条件やパスが偽と評価されるシナリオのみを要求する。
状態遷移図の書き方
-
状態を書き出す

-
遷移を矢印でつなぐ
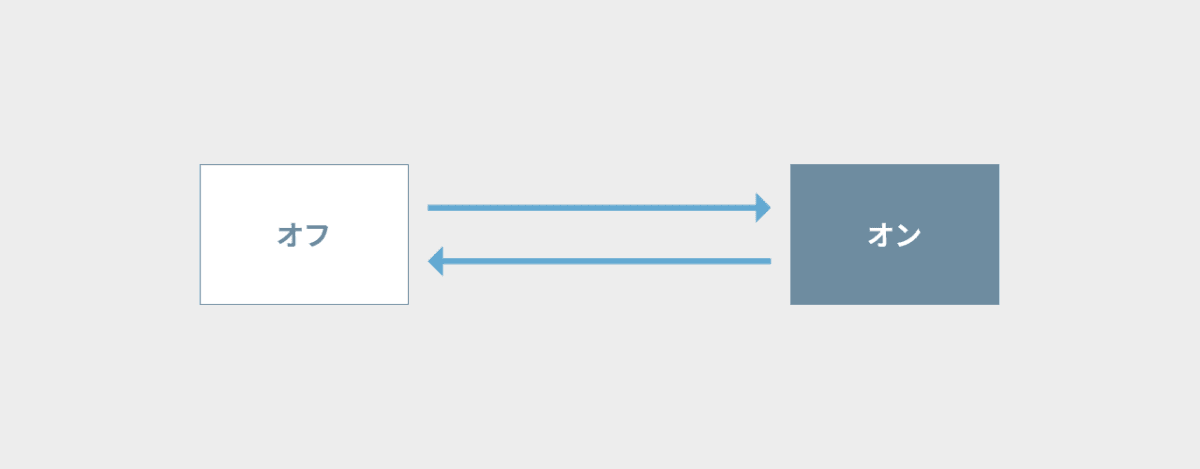
-
イベントを矢印のそばに記入する
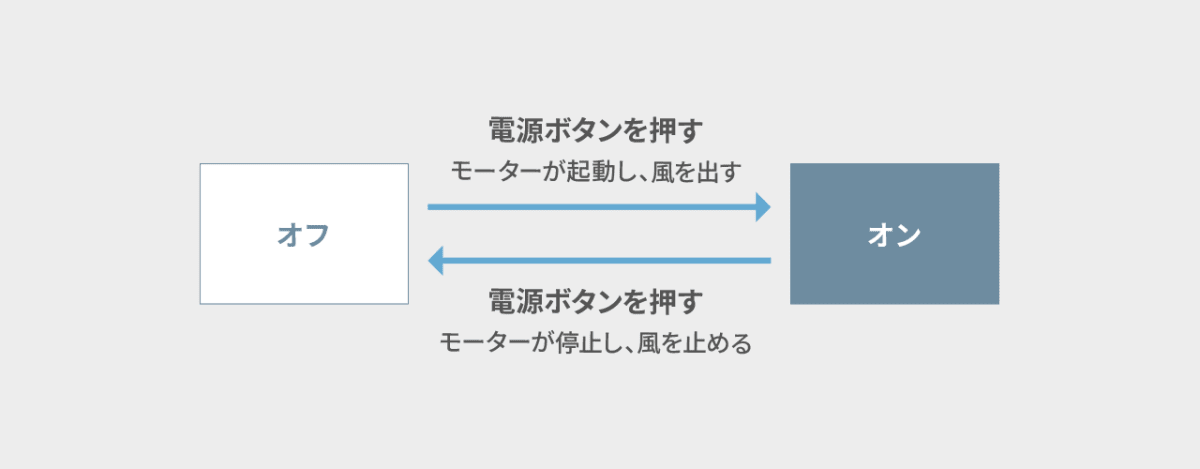
状態遷移表の書き方
- 横軸にイベント、縦軸に遷移前の状態を記載する
- 各状態がイベントを経ることで変化した結果を記載

※ 引用元
組合せテスト
複数の条件を組み合わせてシステムの動作を確認するテスト技法。
「単一の条件では発生しないけれど、複数の条件が組み合わさった際に発生する欠陥」を検出できる。
テスト対象における条件を「因子」、各条件が取りうるパターンを「水準」と呼ぶ。
【例】
| 因子 | OS | ブラウザ | 言語 |
|---|---|---|---|
| 水準 | Windows | Microsoft Edge | 日本語 |
| macOS | Chrome | 英語 | |
| Linux | Firefox | 中国語 | |
| - | Safari | - |
任意にn列(つまりn因子)を選んだときの水準の組み合わせがすべて1回以上現れるようにする組み合わせを「n因子間網羅」という。
直交表
どのn因子を選んだとしても、同数の組み合わせパターンが含まれる表のこと。
下記のように、どの2因子の組み合わせ(AB/AC/AD/BC/BD/CD)においても、「××」「×○」「○×」「○○」がそれぞれ2回ずつ出現する。同様に、どの3因子を組み合わせても同数のパターンが含まれる。
| No. | 因子A | 因子B | 因子C | 因子D |
|---|---|---|---|---|
| 1 | ✕ | ✕ | ✕ | ✕ |
| 2 | ✕ | ✕ | ○ | ○ |
| 3 | ✕ | ○ | ✕ | ○ |
| 4 | ✕ | ○ | ○ | ✕ |
| 5 | ○ | ✕ | ✕ | ○ |
| 6 | ○ | ✕ | ○ | ✕ |
| 7 | ○ | ○ | ✕ | ✕ |
| 8 | ○ | ○ | ○ | ○ |
後述するオールペア法(ペアワイズ法)よりも網羅性を高めやすい。
その反面、テストケース数が増大しやすく、パターン作成の難易度が高いのがデメリット。
オールペア法(ペアワイズ法)
どの2因子を選んだとしても、最低1回以上の組み合わせパターンが含まれる表のこと。
因子数が最小の「2」でよく、パターンの登場回数にバラつき・重複があっても構わない。
下記のように、どの2因子の組み合わせ(AB/AC/AD/BC/BD/CD)においても、「××」「×○」「○×」「○○」がそれぞれ最低1回以上は出現する。
| No. | 因子A | 因子B | 因子C | 因子D |
|---|---|---|---|---|
| 1 | ○ | ○ | ✕ | ○ |
| 2 | ○ | ✕ | ○ | ✕ |
| 3 | ✕ | ○ | ○ | ✕ |
| 4 | ✕ | ✕ | ✕ | ✕ |
| 5 | ✕ | ✕ | ○ | ○ |
組み合わせテストの手順
- 因子の洗い出し
- 因子ごとの水準の洗い出し
- 禁則組み合わせの除外
例えば、iOSやmacOS向けのブラウザ「Safari」は、Windowsでは使えない。
そのため、Windows×Safariというパターンは禁則組合せといえる。
アウトプット書籍
Discussion