Zenn
Closed1

カルマンフィルタを用いたノイズ除去

Python
0y00y0

はじめに

カルマンフィルタの実装は以下で公開しています。
これを使ってノイズ除去をやってみようと思います。
https://github.com/s4k10503/KalmanFilterImplementations

実践

今回はpythonですすめます。

import numpy as np
from kalman_filter import KalmanFilter

データ生成

まず、ノイズが加えられたデータを生成してみます。これは、時間に対して直線的に増加する信号にガウス型のノイズを追加したものです。

# Create synthetic linear data with noise
np.random.seed(0)
dt = 0.1
t = np.arange(0, 10, dt)
x_true = t
noise_std = 3.0
z = x_true + np.random.normal(0, noise_std, size=t.shape)

カルマンフィルタの初期化

次に、カルマンフィルタを初期化します。
状態遷移行列、観測行列、初期状態、初期状態共分散、プロセスノイズ共分散、および観測ノイズ共分散を設定します。

# Initialize the Kalman Filter
F = np.array([[1, dt], [0, 1]])  # state transition matrix
H = np.array([[1, 0]])  # observation matrix
x = np.zeros((2, 1))  # initial state
P = np.eye(2)  # initial state covariance
Q = np.eye(2) * 0.001  # process noise covariance
R = np.array([[noise_std**2]])  # measurement noise covariance
B = np.zeros((2, 1))  # control input matrix
u = np.zeros((1, 1))  # control input
kf = KalmanFilter(F, B, H, x, P, Q, R)

ノイズ除去

ノイズの大きな観測データに対してカルマンフィルタを適用し、信号を推定します。

x_est = np.zeros_like(z)
for i in range(len(t)):
    kf.predict(u)
    kf.update(np.array([[z[i]]]]))
    x_est[i] = kf.get_current_state()[0, 0]

結果

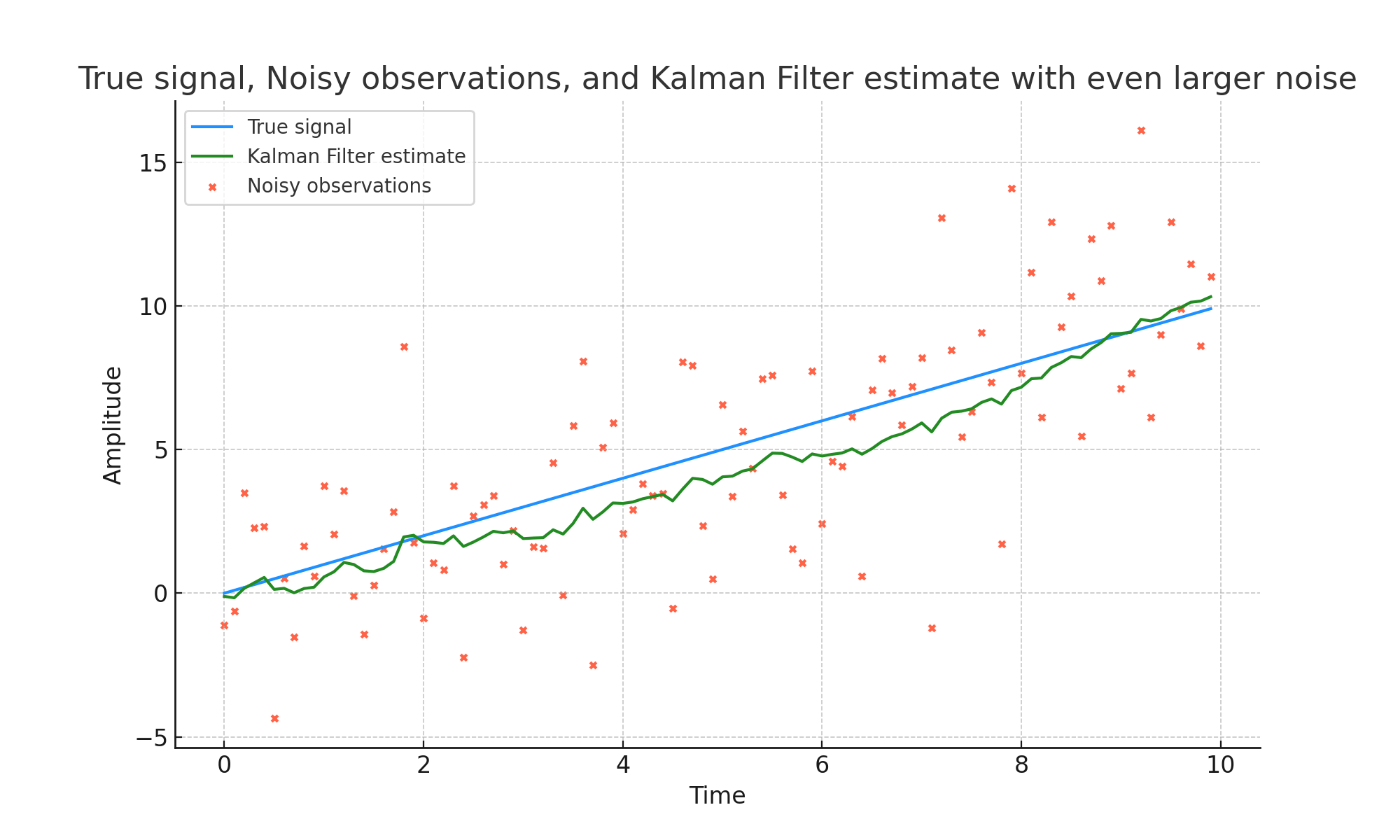
最後に、真の信号、ノイズを含む観測値、そしてカルマンフィルタによる推定をプロットしてみます。

# Plot the true signal, the noisy observations, and the Kalman Filter estimates
plt.figure(figsize=(10, 6))
plt.plot(t, x_true, label='True signal', color='dodgerblue')
plt.scatter(t, z, color='tomato', s=10, label='Noisy observations')
plt.plot(t, x_est, label='Kalman Filter estimate', color='forestgreen')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('True signal, Noisy observations, and Kalman Filter estimate with even larger noise')
plt.grid(True)
plt.show()

おわりに

実装はシンプルですが、動作確認できました

このスクラップは2023/08/09にクローズされました