【教師なし学習】ガラスの成分でクラスタリングしてみよう!
はじめに
こんにちは、コジです!本日はガラスの化学成分の数値を使って教師なし学習のクラスタリングを行なっていこうと思います!
クラスタリングはアルゴリズムを使って機械にグルーピングしてもらうことですね。ガラスの化学成分の数値なんて見ても僕には違いがわからないので、機械に任せてしまおうと話です!
今回の目標は実装して、結果の可視化までをやっていきます!よろしくお願いします!
クラスタリングについて
データのレコードにはカラム(列)がありますよね。例えば100個カラムがあったとしたら、そのレコードは100次元の点の一つです。それぞれの点の距離が近いものを一つのグループとして扱う、また点、もしくはグループの距離が近いものを一つのグループとして扱う、というのを繰り返してグルーピングしていくのがクラスタリングです!
分類とクラスタリングの違い
グルーピングしていくって分類も似たようなことしている気が、、、
分類は教師あり学習です。使用するモデルはどのグループに所属するかの答えをもと作られます。そしてそのモデルを用いて、未知のデータがどのグループに所属するかを予測します。
クラスタリングは教師なし学習です。どのグループに所属するなどの答えはなく、データをもとに特徴を学習しグループ分けします。
違いがわかったところで、クラスタリングには2つ種類あるので、違いを紹介します!
階層型クラスタリング
全ての点同士の距離を測り、クラスタリングを行います。
メリット
- 施策ごとに結果が常に一定。
- 樹形図(デンドログラム)で結果を可視化できる。
- 何個のクラスタ(グループ)に分けるかは結果を見てから決められる。
デメリット
- 全ての点同士の距離を計算するため、計算量が膨大。
非階層型クラスタリング
階層を作らずにデータのクラスタリングを行います。母集団の中で距離の近いデータをまとめて、予め指定した数のクラスタに分類していきます。
k-meansというアルゴリズムが有名で、ランダムで基準点を決めてそれぞれの点との距離を計算する。
ここのサイトでアルゴリズムを可視化したアニメーションが見れるので面白いです。
メリット
- 計算量が少ない。
デメリット
- 事前にクラスタ数を決めておく必要がある。
- 結果が初期値に依存してしまう。
実装
それでは早速実装していきましょう!
環境
- colab
階層型クラスタリング
まずはsignateのサイトからダウンロードしてきたtrain.tsvファイルを読み込みましょう!
import numpy as np
import pandas as pd
# ファイルの読み込み
data_path = '/content/drive/MyDrive/glass.tsv'
# tsvを読み込んでデータフレームにする。
df = pd.read_csv(data_path, sep="\t")
print('titanic_dataframe\n{}\n'.format(df.head()))
| index | Unnamed: 0 | RI | Na | Mg | Al | Si | K | Ca | Ba | Fe | Type |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1.5172 | 13.38 | 3.5 | 1.15 | 72.85 | 0.5 | 8.43 | 0.0 | 0.0 | 1 |
| 1 | 1 | 1.51631 | 13.34 | 3.57 | 1.57 | 72.87 | 0.61 | 7.89 | 0.0 | 0.0 | 2 |
| 2 | 3 | 1.52043 | 13.38 | 0.0 | 1.4 | 72.25 | 0.33 | 12.5 | 0.0 | 0.0 | 5 |
| 3 | 6 | 1.51793 | 13.21 | 3.48 | 1.41 | 72.64 | 0.59 | 8.43 | 0.0 | 0.0 | 1 |
| 4 | 9 | 1.523 | 13.31 | 3.58 | 0.82 | 71.99 | 0.12 | 10.17 | 0.0 | 0.03 | 1 |
僕は化学苦手で、元素記号うろ覚えなので、同じ状況の方のために下記をどうぞ!
| カラム | ヘッダ名称 | データ型 | 説明 |
|---|---|---|---|
| 0 | Unnamed: 0 | int | インデックスとして使用 |
| 1 | RI | float | 屈折率 |
| 2 | Na | float | ナトリウム |
| 3 | Mg | float | マグネシウム |
| 4 | Al | float | アルミニウム |
| 5 | Si | float | シリコン |
| 6 | K | float | ポタシウム |
| 7 | Ca | float | カルシウム |
| 8 | Ba | float | バリウム |
| 9 | Fe | float | 鉄 |
| 10 | Type | int | ガラスの種類 (1=building_windows_float_processed, 2=building_windows_non_float_processed, 3=vehicle_windows_float_processed, 5=containers, 6=tableware, 7=headlamps)※4は無し |
それではデータの情報を確認していきましょう!
df.info()
# -----------------------------------------
# <class 'pandas.core.frame.DataFrame'>
# RangeIndex: 107 entries, 0 to 106
# Data columns (total 11 columns):
# # Column Non-Null Count Dtype
# --- ------ -------------- -----
# 0 Unnamed: 0 107 non-null int64
# 1 RI 107 non-null float64
# 2 Na 107 non-null float64
# 3 Mg 107 non-null float64
# 4 Al 107 non-null float64
# 5 Si 107 non-null float64
# 6 K 107 non-null float64
# 7 Ca 107 non-null float64
# 8 Ba 107 non-null float64
# 9 Fe 107 non-null float64
# 10 Type 107 non-null int64
# dtypes: float64(9), int64(2)
# memory usage: 9.3 KB
今回は欠損値もなく文字列もないので、データ加工は必要なさそうです。
Typeのカラムは答えになってしまうので、分けてしまいましょう!
# 正解データ
y = df['Type']
# 特徴量データ
x = df.drop(columns='Type')
それでは実装に移りましょう!
from scipy.cluster.hierarchy import linkage
# 指数表記を禁止する
np.set_printoptions(suppress=True)
# 階層型クラスタリング
result = linkage(x)
result
# ---------------------------------------------------------
# [[ 88. , 89. , 1.04207759, 2. ],
# [ 90. , 107. , 1.06329677, 3. ],
# [ 72. , 73. , 1.11910687, 2. ],
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# [204. , 207. , 8.13156812, 53. ],
# [205. , 209. , 8.39260991, 54. ],
# [210. , 211. , 9.29072674, 107. ]]
はい!なっがい2次元リストが出てきましたね!
これはクラスタリングのログなのですが、見方として
[クラスタ1のindex, クラスタ2のindex, 距離, データの数]
となっています。
ですので、1~2行目を例にとって説明すると、
- index
88と89の距離は1.04207759でデータの数は2つ - index
90と107の距離は1.06329677でデータの数は3つ
となります。2行目のデータ数が「3」なのは88と89と90の3データのことですね!
これでは、わかりづらいのでデンドログラムをプロットしてみましょう!
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.cluster.hierarchy import dendrogram
# 表示サイズを変更
plt.figure(figsize=(30, 16))
# デンドログラム(樹形図をプロット)
dendrogram(result)
plt.title("Dedrogram")
plt.ylabel("Threshold", fontsize=13)
plt.tick_params(labelsize=13)
plt.show()
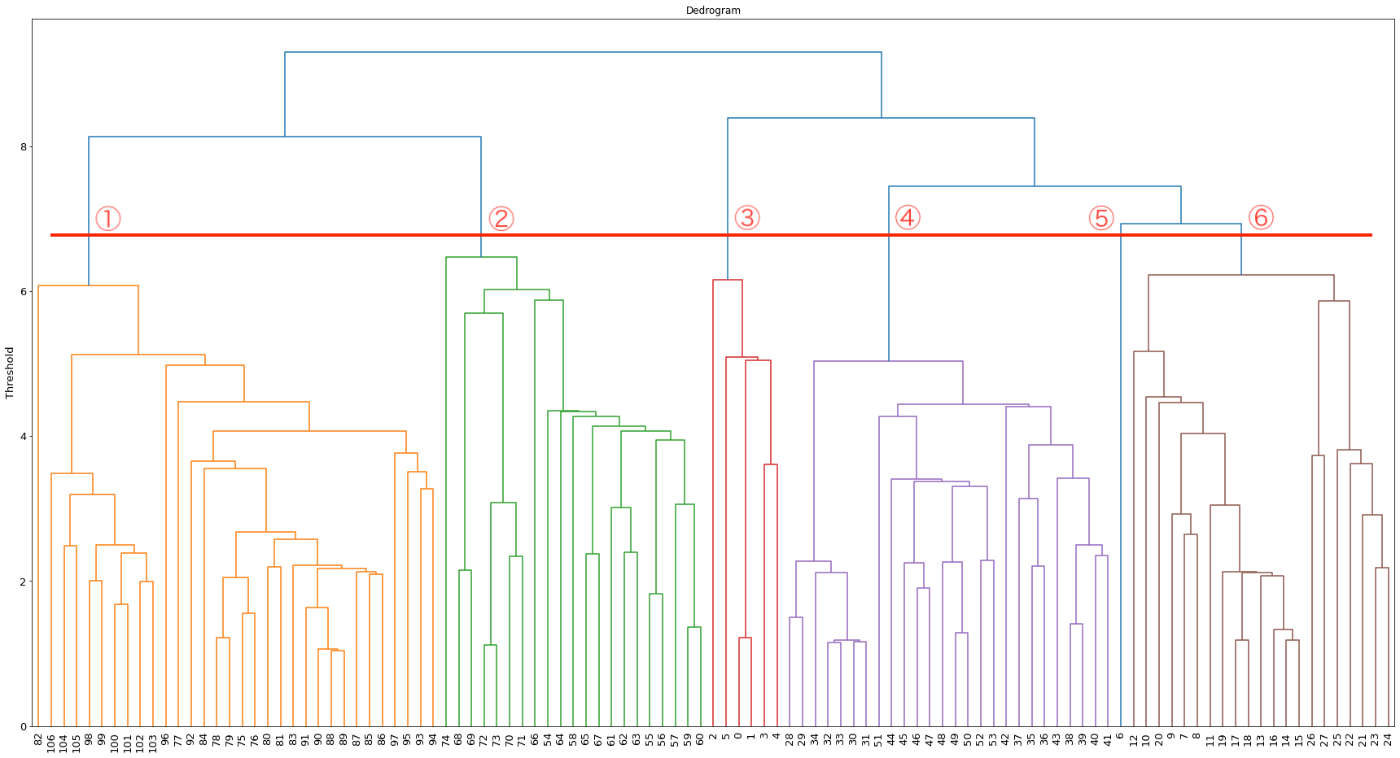
おぉ!なんかすごいし、感動しますね!
※X軸の数字が見づらいと思うので、クリックして拡大して見てください!
これを見ればどの辺でクラスタ数を分けようかわかりやすいですね。
print(f'クラスタ数:{y.nunique()}')
# --------------------------------
# クラスタ数:6
今回はTypeが6種類なので画像の赤線のところで区切れますね!
非階層型クラスタリング
次はK-meansでクラスタリングを行いましょう!
データは同じものを使います!
from sklearn.cluster import KMeans
# 非階層型クラスタリング
# k-meansを6個に分類でインスタンス化
cluster_k_retry = KMeans(n_clusters=6)
# クラスタリング
result_k_retry = cluster_k.fit(x_retry)
k-meansを使う際には先にクラスタ数を決めておくので、n_clusters=6に設定します。
次は結果の可視化ですが、k-meansは非階層型クラスタリングなのでデンドログラムはプロットできません。。。
色々調べてみた結果、主成分分析を行えば良いようです。
主成分分析を使い、次元削減で10次元 => 2次元にすることで、結果の可視化が可能になるので、実践してみましょう!
from sklearn.decomposition import PCA
# PCAを2次元でインスタンス化
pca = PCA(n_components=2)
# 主成分分析の実行
pca.fit(x)
# データを主成分に変換する
x_pca = pca.transform(x)
# データフレーム化
pca_df = pd.DataFrame(x_pca)
# 各主成分が持つ分散の比率
print(pca.explained_variance_ratio_)
# -----------------------------------
# [0.99864065 0.00073186]
一つ目の成分が99.86%の情報を持っているようです。
合計すると99.94%になるので、情報はほどんどかけていませんね。
それではプロットしてみましょう。
fig = plt.figure(figsize = (8, 8))
plt.scatter(pca_df[0], pca_df[1], c=result_k.labels_,)
plt.show()
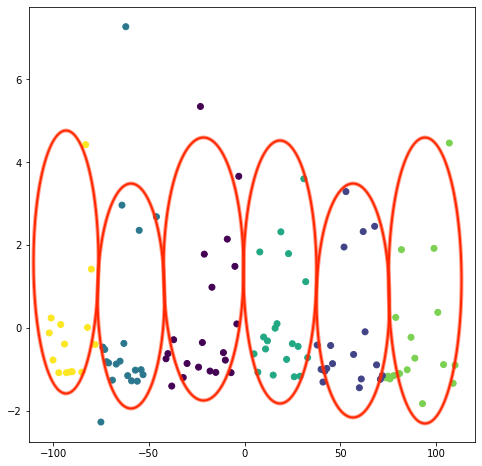
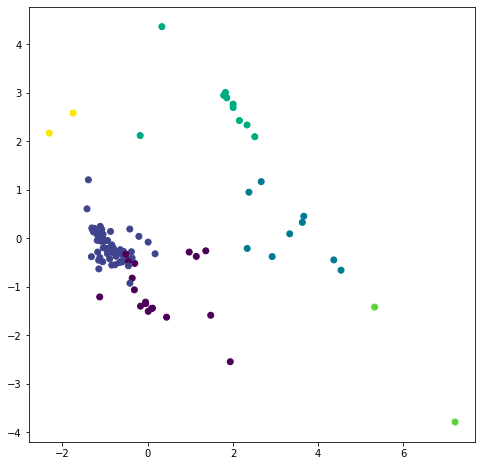
縦長にグルーピングされていますね!
では、実際の正解データでもプロットしてみましょう。
fig = plt.figure(figsize = (8, 8))
plt.scatter(pca_df[0], pca_df[1], c=y)
plt.show()
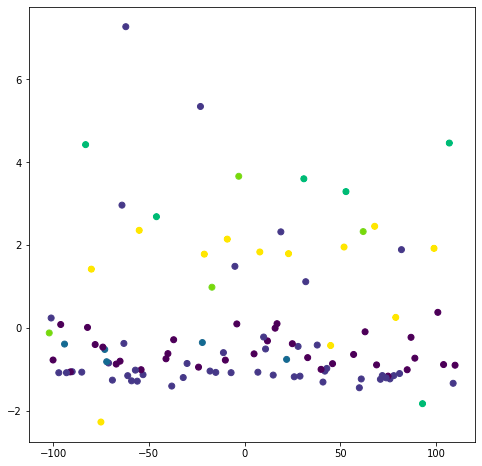
あれ?結果が先ほどのグラフとかなりずれていますね、、、
何かがおかしい、、、
クラスタリングした結果のラベルを見てみましょう。
result_k.labels_
# --------------------------------------
# array([4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3,
# 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
# 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
# 2, 2, 2, 2, 2, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5],
# dtype=int32)
???こんなに綺麗にラベルが分かれるでしょうか??
クラスタリングがうまっくいっていないようなので、色々見返してみると、原因がありました!
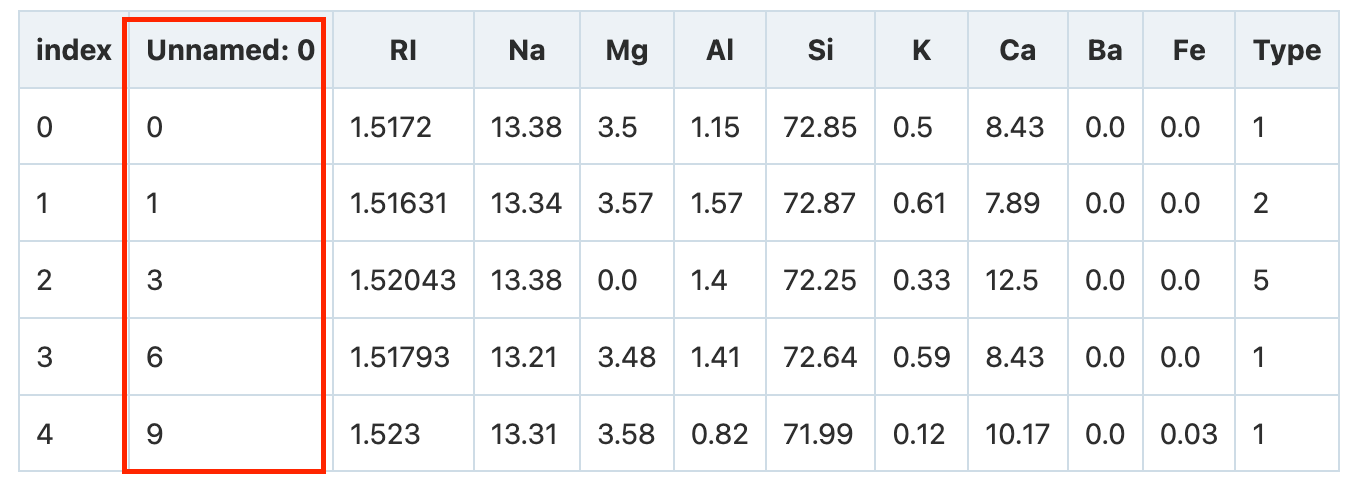
-
Unnamed: 0
こいつですね!インデックスとして使用されるカラムを残したまま、処理していたからでした。
データは実装前にじっくり確認することの大事さを学びました。。。
それでは気を取り直して、もう一度やってみましょう!
階層型クラスタリング(やり直し)
# 正解データの取り出し
# 正解データ
y_retry = df['Type']
# 特徴量データ
x_retry = df[['RI', 'Na', 'Mg', 'Al', 'Si', 'K', 'Ca', 'Ba', 'Fe']]
今度は特徴量データxをドロップではなく、カラム指定して取り出します!
# クラスタリング
result_retry = linkage(x_retry, method='ward', metric='euclidean')
他の引数も指定してみます!
methodはクラスタリングの手法で今回はウォード法を、
metricは距離の測り方でユークリッド距離を使ってみました。
初期値はmethodは'single'、metricは'euclidean'です。
ウォード法やユークリッド距離の他にも色々あるので、調べて試してみてください!
# デンドログラム(樹形図をプロット)
dendrogram(result_retry, labels=y_retry.tolist())
plt.title("Dedrogram")
plt.ylabel("Threshold", fontsize=13)
plt.tick_params(labelsize=13)
plt.show()
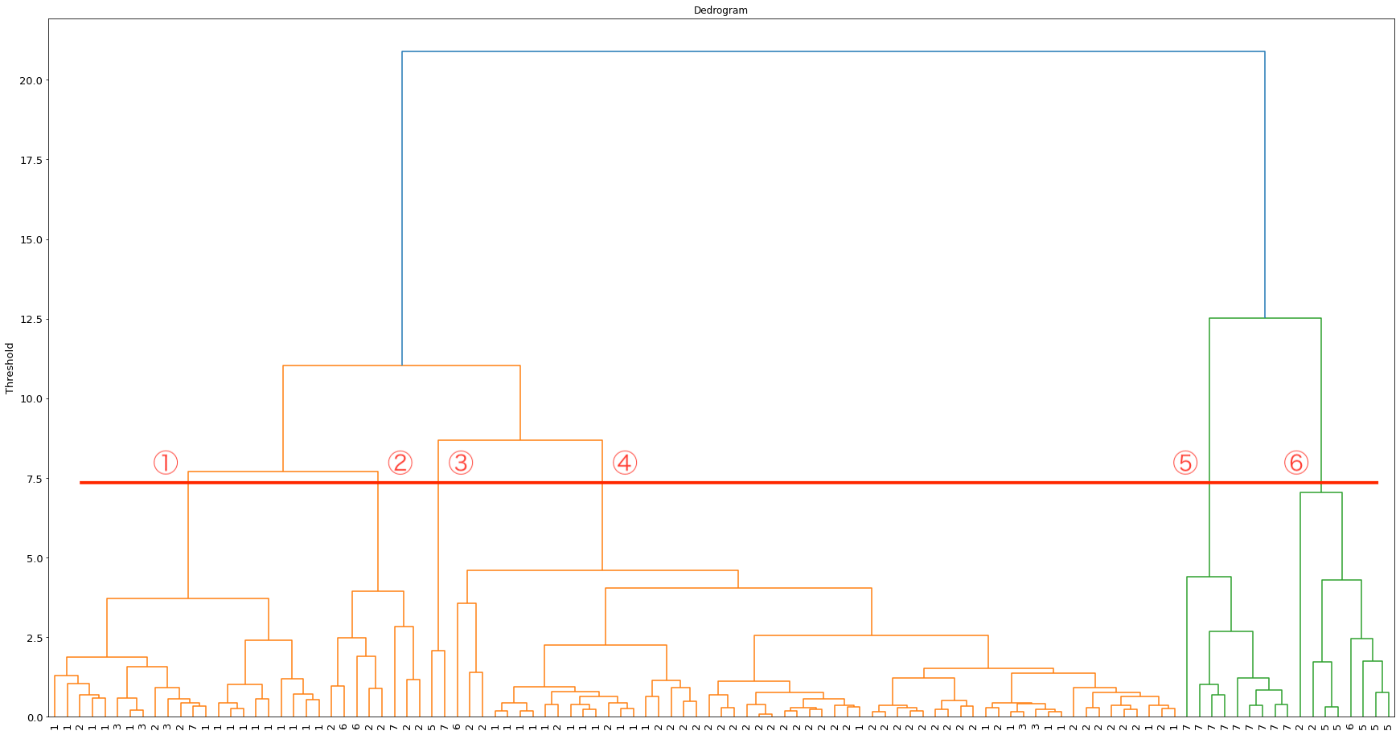
はい!綺麗なデンドログラムですね!
今回はX軸のラベルを正解データに置き換えてみました。
結構いい感じにTypeの数字が分かれていますね!
非階層型クラスタリング(やり直し)
次はK-meansです!
# 非階層型クラスタリング
# k-meansを6個に分類でインスタンス化
cluster_k_retry = KMeans(n_clusters=6)
# クラスタリング
result_k_retry = cluster_k.fit(x_retry)
result_k_retry.labels_
# --------------------------------------
# array([1, 1, 2, 1, 0, 3, 5, 1, 0, 1, 0, 1, 3, 1, 1, 1, 1, 1, 1, 1, 3, 0,
# 2, 1, 1, 1, 2, 3, 1, 1, 1, 1, 1, 1, 1, 1, 0, 2, 1, 1, 1, 0, 3, 1,
# 2, 0, 1, 1, 0, 1, 1, 3, 1, 1, 2, 0, 0, 1, 3, 1, 1, 1, 0, 1, 3, 1,
# 4, 1, 1, 1, 0, 1, 1, 1, 2, 1, 1, 3, 1, 1, 1, 1, 4, 1, 2, 1, 1, 1,
# 1, 1, 1, 0, 5, 0, 0, 0, 2, 1, 1, 0, 1, 1, 0, 1, 1, 1, 3],
# dtype=int32)
結果のラベルも良さそうな感じですね!
# 結果を可視化しやすくするためにPCAでデータを2次元に削減する
# PCAを2次元でインスタンス化
pca_retry = PCA(n_components=2)
# 主成分分析の実行
pca_retry.fit(x_retry)
# データを主成分に変換する
x_pca_retry = pca_retry.transform(x_retry)
# データフレーム化
pca_df_retry = pd.DataFrame(x_pca_retry)
# 各主成分が持つ分散の比率
print(pca_retry.explained_variance_ratio_)
# --------------------------------------------
# [0.53588955 0.26318788]
分散比率は合計すると79.91%なので、20%ほど元のデータから情報が落ちてしまっています。
やはり最初の分散比率が99%超えはおかしかったのですね。そこでも気づくべきでした、、、
# 結果を出力
fig = plt.figure(figsize = (8, 8))
plt.scatter(pca_df_retry[0], pca_df_retry[1], c=result_k_retry.labels_)
plt.show()
実際の正解データでもプロットしてみましょう。
# 結果を出力
fig = plt.figure(figsize = (8, 8))
plt.scatter(pca_df_retry[0], pca_df_retry[1], c=y)
plt.show()
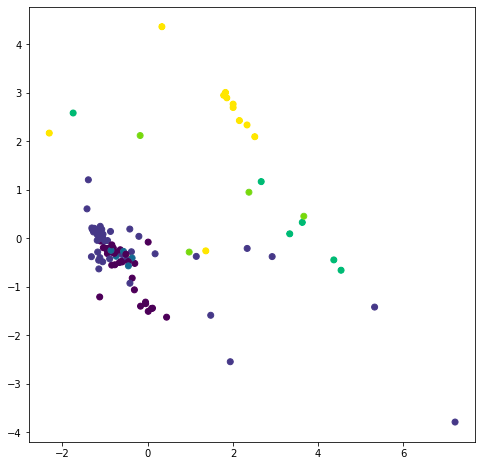
類似したプロットになっていますね!
せっかくなので、全てのデータを横方向に結合してみましょう。
# データを結合
kmeans_label = pd.DataFrame()
kmeans_label['kmeans_label'] = result_k_retry.labels_
df_result = pd.concat([x_retry, pca_df_retry, y_retry, kmeans_label], axis=1)
df_result.head(10)
| index | RI | Na | Mg | Al | Si | K | Ca | Ba | Fe | 0 | 1 | Type | kmeans_label |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.5172 | 13.38 | 3.5 | 1.15 | 72.85 | 0.5 | 8.43 | 0.0 | 0.0 | -0.819 | -0.194 | 1 | 1 |
| 1 | 1.51631 | 13.34 | 3.57 | 1.57 | 72.87 | 0.61 | 7.89 | 0.0 | 0.0 | -1.254 | 0.208 | 2 | 1 |
| 2 | 1.52043 | 13.38 | 0.0 | 1.4 | 72.25 | 0.33 | 12.5 | 0.0 | 0.0 | 4.537 | -0.656 | 5 | 3 |
| 3 | 1.51793 | 13.21 | 3.48 | 1.41 | 72.64 | 0.59 | 8.43 | 0.0 | 0.0 | -0.808 | -0.2 | 1 | 1 |
| 4 | 1.523 | 13.31 | 3.58 | 0.82 | 71.99 | 0.12 | 10.17 | 0.0 | 0.03 | 0.443 | -1.625 | 1 | 5 |
| 5 | 1.51617 | 14.95 | 0.0 | 2.27 | 73.3 | 0.0 | 8.71 | 0.67 | 0.0 | 2.005 | 2.699 | 7 | 0 |
| 6 | 1.51514 | 14.01 | 2.68 | 3.5 | 69.89 | 1.68 | 5.87 | 2.2 | 0.0 | -1.750 | 2.586 | 5 | 4 |
| 7 | 1.51793 | 12.79 | 3.5 | 1.12 | 73.03 | 0.64 | 8.77 | 0.0 | 0.0 | -0.665 | -0.498 | 1 | 1 |
| 8 | 1.52172 | 13.51 | 3.86 | 0.88 | 71.79 | 0.23 | 9.54 | 0.0 | 0.11 | -0.168 | -1.397 | 1 | 5 |
| 9 | 1.51763 | 12.61 | 3.59 | 1.31 | 73.29 | 0.58 | 8.5 | 0.0 | 0.0 | -0.945 | -0.313 | 1 | 1 |
Typeとk-means_labelは異なりますが、クラスタリングでどのように分類したのか確認できますね。
例えば、k-means_labelが1の部分を見てみるとカルシウム(Ca)が8.00前後で分類されているようです。
そのほかにもバリウムがたくさん含まれていると4に分類されているのでしょうか?(全データを見てみないとわかりませんが、、、)
このようにクラスタリングされた結果を見てどう分類されているか、また、ガラスのサンプルが目の前にあるならそれぞれを見比べることも可能ですね。
まとめ
今回の記事ではクラスタリングの実装をしてみました。
実装観点では、やはりデータの確認を怠ってしまったことでしょう。反省してます。。。
そのほかにも、次元削減や主成分分析も今回結果を可視化する段階で使用できたので、知見が深まりました。
ビジネス観点では、私たちが分類しづらかったり、思いつかないジャンル分けしてくれたりと知見を得るために利用されるのだと、実装を通して改めて納得しました。いろんなデータでも試してみたいと感じました。
Discussion