Zenn
👨‍💻

LeetCode: 169. Majority Element をGoで解く

2024/09/22に公開
LeetCode
tech

LeetCodeの問題を解いたら、記録することにした。Goで解く。

問題

169. Majority Element

numsというsizeがnの配列が与えられ、その中の過半数を占める数字を返すというもの。
例えば、nums = [2,2,1,1,1,2,2]が与えられたら、解は2。

難易度はeasyにカテゴライズされる。

制約

n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109

過半数を占める数字は必ず存在する。

解いてみる

ぱっと思いついた解き方

ぱっと思いついたのは、各数字の出現回数を記録して、一番多いものを返せば良さそう。
この手の重複考慮系のものはmapを使えば大体なんとかなる。解くことだけを目的にするなら確かに難易度はeasyかも。

solution.go
func majorityElement(nums []int) int {
    numCountMap := make(map[int]int)
    for _, num := range nums {
        numCountMap[num]++
    }
    var majority, majorityCount int 
    for num, count := range numCountMap {
        if count > majorityCount {
            majority = num
            majorityCount = count
        }
    }
    return majority
}

これを実行すると、ちゃんとPassした。

  • Runtime 22ms (Beats 28.56%)
  • Memory 6.66mb (Beats 65.90%)

ただし

  • Time Complexity O(N)
  • Space Complexity O(N)

numsの1重ループをしてるのと、numsの長さに依存した大きさとなるmapを定義しているから、当然か。

これだと、フォローアップの「Could you solve the problem in linear time and in O(1) space?」を実現できない。。

Boyer-Moore Voting Algorithmで解く

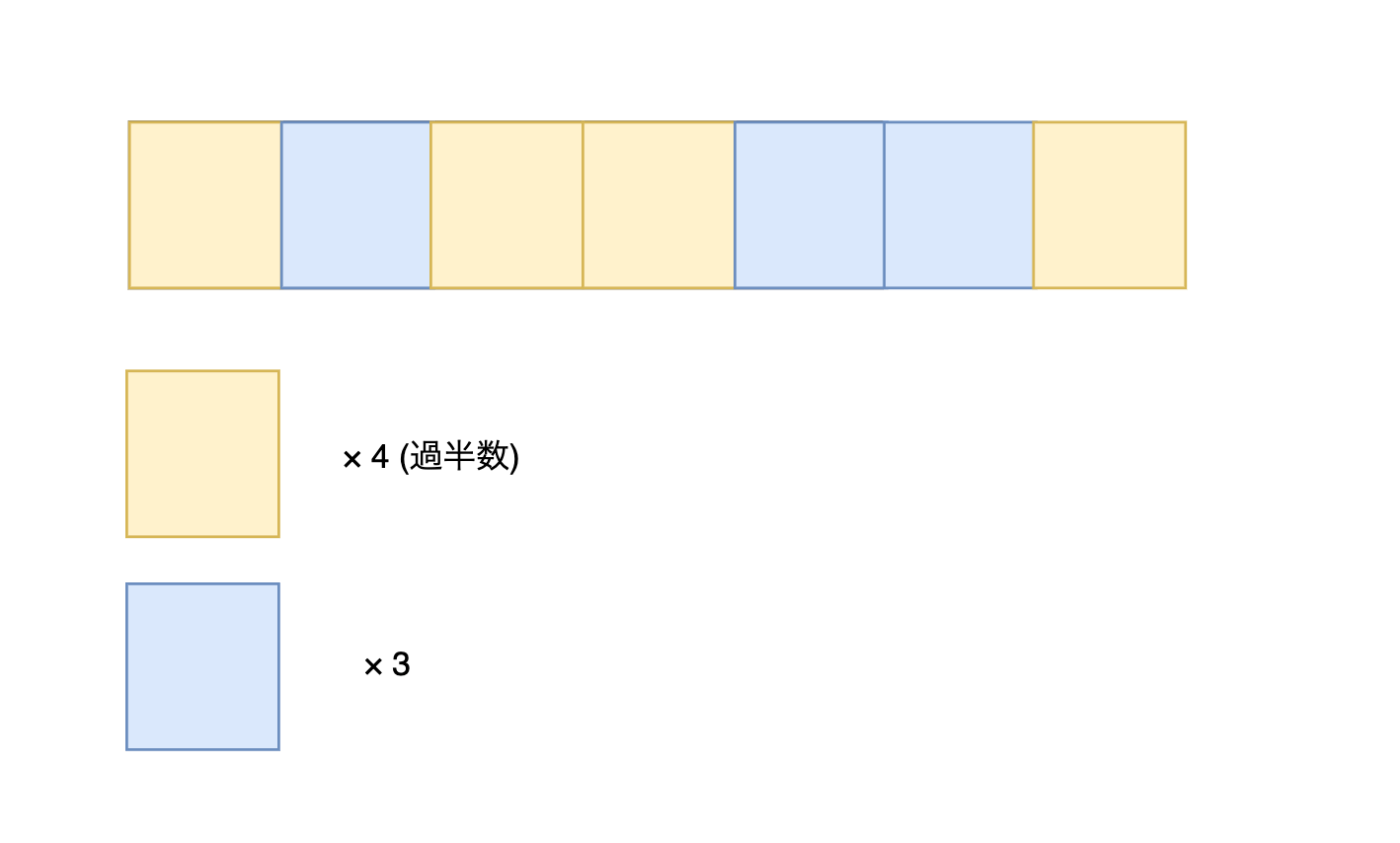
Boyer-Moore Voting Algorithmは過半数を占める要素を特定するアルゴリズム。
過半数候補(candidate)とカウント(count)の2つの概念を使って、過半数を占めるものを見つける。
ざっくり、過半数の要素の数 - それ以外の要素の数 > 0　となることを利用して、過半数の要素を特定する。

フローチャートにすると以下。

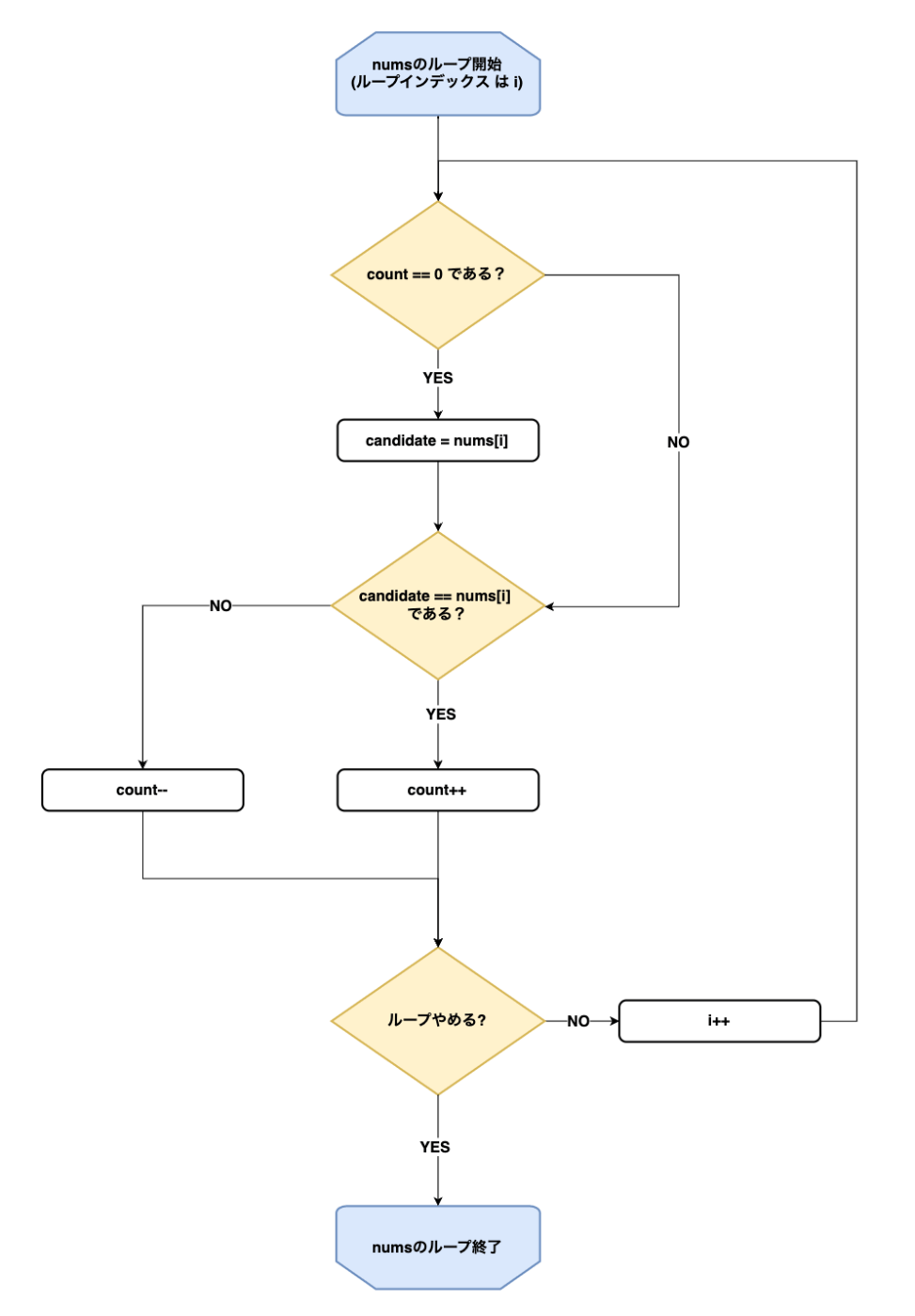
Goにすると以下

solution.go
func majorityElement(nums []int) int {
	var candidate, count int
	for _, num := range nums {
		if count == 0 {
			candidate = num
		}
		if candidate == num {
			count++
		} else {
			count--
		}
	}
	return candidate
}

これを実行すると、ちゃんとPassした。

  • Runtime 13ms (Beats 94.73%)
  • Memory 6.52mb (Beats 81.24%)

そして、特にnに依存したmapの作成をやめたので、

  • Time Complexity O(N)
  • Space Complexity O(1)

となった。

参考

https://qiita.com/tatmius/items/37707bce1ef079616c93

Discussion