Zenn
🌊

STLの仕組みを理解してパラメータを適切に設定する【Python】【statsmodels】

2024/09/11に公開
Python
時系列
時系列分析
statsmodels
tech

1. 概要

1.1 本記事の目的

本記事では、時系列データを「トレンド」「季節性」「残差」の3要素に分解するSTL[1](Seasonal Trend decomposition using Loess)について解説します。
具体的には、以下２点を理解することで、STL実行時に適切なパラメータを設定できるようになることを目指します。

  • STLで使用される平滑化手法Loessのアルゴリズム
  • STLのアルゴリズム

1.2 STLの概要

STLでは時系列データを以下の3要素に分解します。

  • トレンド(Trend)
    時系列の長期的な傾向
  • 季節性(Seasonal)
    一定期間で繰り返す周期的な変動(例: 日、週、月、年)
    季節性の周期の長さは事前にパラメータで設定
  • 残差(Remainder)
    トレンドや季節性で説明できない、不規則な変動成分

時系列データをこれらの要素に分解することで、データの特徴をより明確に理解し、より正確な予測を立てるのに役立ちます。

STLでは、滑らかで解釈しやすいトレンドや季節性を抽出するためにLoessという手法が用いられています。そのため、STLのパラメータにはLoessに関するパラメータも含まれており、Loessについての理解が必要不可欠です。
本記事では、2章でLoess、3章でSTLのアルゴリズム、4章でstatsmodelsのSTLのパラメータについて解説します。

2. Loess

Loess(Locally Estimated Scatterd Smoothing)は局所回帰の一手法で、STLにおいて季節性やトレンド等の平滑化に使用されます。以下でLoessのアルゴリズムを説明します。

2.1 基本的な平滑化アルゴリズム

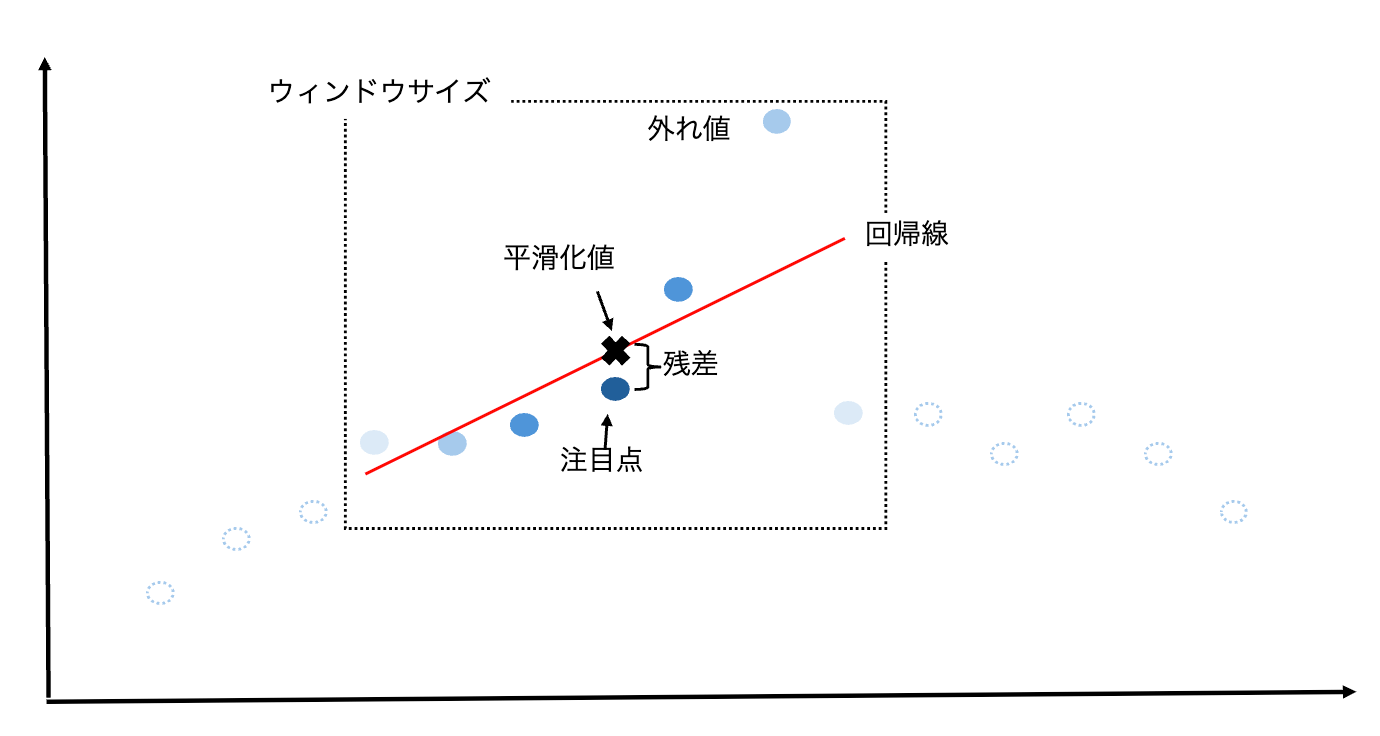
注目する点を1点ずつずらしながら、以下手順を行います。

  1. 注目する点の近傍点に対して、「近傍重み」(2.3参照)を計算する
    • 使用する近傍点の数はパラメータ「ウィンドウサイズ」で事前に指定
  2. 重み付き最小二乗法による回帰を行う
    • 回帰に用いる多項式の次数はパラメータで事前に指定(一般的には1次または2次を使用)
  3. 注目している点の回帰結果を平滑化値とする
  4. 手順1~3を全ての点に対して実行

2.2 外れ値への対応

基本的な平滑化では、外れ値が回帰線に大きな影響を与える可能性があります。そこで、以下の追加手順を行います。

  1. 全ての点に対して、平滑化値と元の値との残差を求める
  2. 残差から「ロバスト重み」(2.4参照)を計算する
  3. 近傍重みとロバスト重みの両方を使用して、手順2~4を再実行
  4. 手順5~7を指定回数繰り返す

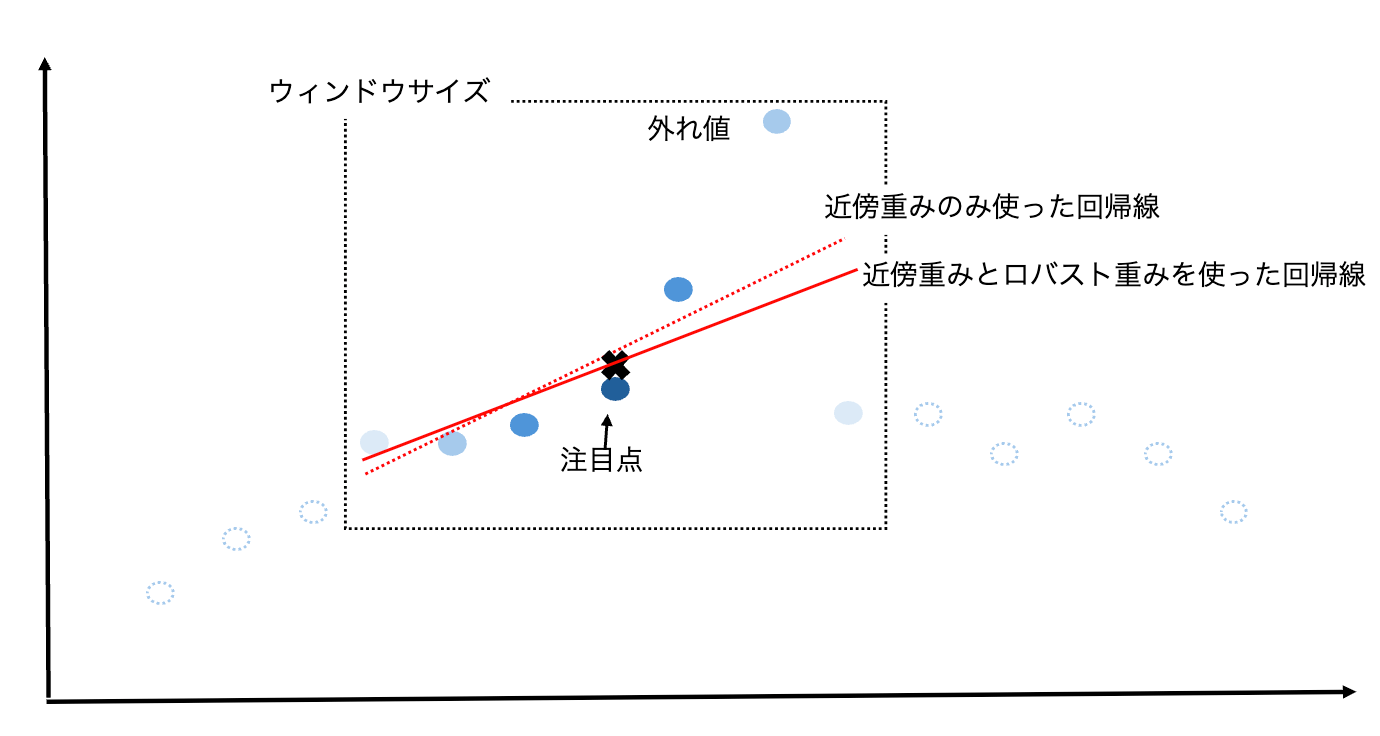
ここで2種類の重みは以下の特徴を持っています。

  • 近傍重み
    注目する点に近い点ほど大きい重みが与えられる
  • ロバスト重み
    外れ値に小さい重みが与えられる

以下で、各重みの計算方法を説明します。(数式が苦手な方は読み飛ばして大丈夫です🙆)

2.3 近傍重みの計算方法

i=1 \sim nとし、説明変数をx_{i}とします。注目する点xの近傍点としてq個の点を選び、そのうち最も遠い点までの距離を\lambda_{q}(x)とします。各点の近傍重みは、以下の関数W(d)を用いて計算します。

\begin{equation} W(d) = \begin{cases} (1-d^{3})^{3} & 0 \leq d < 1 \\ 0 & d \geq 1 \end{cases} \end{equation}

ここで、dは距離を表しており、距離が短いほど(dが0に近いほど)重みが大きくなることがわかります。点x_iの重み\nu_{i}(x)は以下の式で表されます。

\begin{equation} \nu_{i}(x) = W \left(\frac{|x_{i}-x|}{\lambda_{q}(x)}\right) \end{equation}

式(2)より、点x_iがxに近いほど重みが大きくなり、q番目に遠い点では重みが0になることがわかります。また、ウィンドウサイズqを大きくすると\lambda_{q}(x)が大きくなるため、重み\nu_{i}(x)は1に近づき、通常の多項式回帰に近くなります。
つまり、近傍重みは以下の特徴を持つことがわかります。

  • 注目する点に近い点ほど大きな重みを与える
  • ウィンドウサイズqが大きいほど、滑らかな回帰線となる

2.4 ロバスト重みの計算方法

点x_{i}における平滑化値と元データとの残差をr_{i}とします。各点のロバスト重みは、以下の関数B(r)を用いて計算します。

\begin{equation} B(r) = \begin{cases} (1-r^{2})^{2} & 0 \leq r < 1 \\ 0 & r \geq 1 \end{cases} \end{equation}

ここで、rは残差の大きさを表しており、残差が大きいほど(rが大きいほど)重みが小さくなることが分かります。
点x_iの重み\rho_{i}は、以下の式で表されます。

\begin{equation} \rho_{i} = B \left(\frac{|r_{i}|}{6median(|r|)}\right) \end{equation}

式(4)より、残差r_iが大きいほど重みは小さくなり、残差の中央値の6倍以上大きい場合は重みが0になることが分かります。
つまり、ロバスト重みは以下の特徴を持つことがわかります。

  • 外れ値には小さい重みを与える

3. STLのアルゴリズム

3.1 outer loopとinner loop

STLでは、outer loopとinner loopという2種類のループ処理を組み合わせることで、時系列データの分解を行います。

  • outer loop
    inner loopで計算された残差を用いて、ロバスト重みを更新
  • inner loop
    原系列に対して、トレンド・季節性・残差への分解を繰り返す

名前の通り、outer loopの処理の中にinner loopが含まれていて、それぞれのループの反復回数はパラメータで指定します。例えば{outer loop: 5回, inner loop: 2回}とすると、5回のouter loopの中で2回ずつinner loopが実行されます。このようにouter loopとinner loopを複数回繰り返すことで、分解の精度を高めていきます。

inner loopとouter loopのフローチャート

3.2 STLの手順

原系列をY、トレンドをT、季節性をS、残差をRとします。この時、時刻t=1 \sim nにおける各系列の点を、Y_{t}、T_{t}、S_{t}、R_{t}とします。また、k回目の分解で計算されたトレンドをT_{t}^{(k)}、季節性をS_{t}^{(k)}とします。
以下では(k+1)回目の分解の手順を説明し、T_{t}^{(k+1)}、S_{t}^{(k+1)}を計算していきます。

3.2.1 inner loop

1. トレンドの除去
原系列から前回(k回目)の分解で計算されたトレンド成分を除去します。初回の分解では、T_{t}^{(0)}=0とします。

\begin{equation} Y_{t}(detrended) = Y_{t} - T_{t}^{(k)} \end{equation}

2. 周期成分の平滑化
手順1でトレンドを除去したデータから、周期成分C_{t}^{(k+1)}を分解します。周期成分の分解方法が少し分かりにくいため、3.3で詳しく説明します。

\begin{equation} C_{t}^{(k+1)} = Y_{t}(detrended)の周期成分 \end{equation}

3. 平滑化周期成分にローパスフィルタ適用
手順2で計算した平滑化周期成分C_{t}^{(k+1)}に対して、移動平均ローパスフィルタを適用することで、低周波成分(=トレンド成分)を抽出します。さらに、抽出した低周波成分に対してLoess平滑化を適用します。この結果得られる低周波成分をL_{t}^{(k+1)}とします。

\begin{equation} L_{t}^{(k+1)} = C_{t}^{(k+1)}の低周波成分 \end{equation}

4. 周期成分からトレンドを除去
手順2で計算した平滑化周期成分C_{t}^{(k+1)}から、手順3で計算した低周波成分L_{t}^{(k+1)}を除去します。これにより、周期成分からトレンド成分が除去され、季節性S_{t}^{(k+1)}が分解されます。

\begin{equation} S_{t}^{(k+1)} = C_{t}^{(k+1)} - L_{t}^{(k+1)} \end{equation}

5. 季節性の除去
原系列から手順4で計算した季節性S_{t}^{(k+1)}を除去します。

\begin{equation} Y_{t}(deseasonalized) = Y_{t} - S_{t}^{(k+1)} \end{equation}

6. トレンド平滑化
手順5の結果に対してLoess平滑化を適用し、トレンドT_{t}^{(k+1)}を分解します。

\begin{equation} T_{t}^{(k+1)} = Y_{t}(deseasonalized)の平滑化結果 \end{equation}

7. 手順1~6を指定回数繰り返し
パラメータで指定された回数だけ、手順1〜6 を繰り返します。

3.2.2 outer loop

1. 残差を計算
inner loopによって原系列が季節性とトレンドに分解されたので、残差を計算します。

\begin{equation} R_{t} = Y_{t} - T_{t} - S_{t} \end{equation}

2. ロバスト重みを計算
手順1で計算した残差R_{t}を用いて、各時刻におけるロバスト重みを計算します。

3. inner loopの実行
更新されたロバスト重みを用いて、inner loopのを実行します。

3.3 周期成分のLoess平滑化

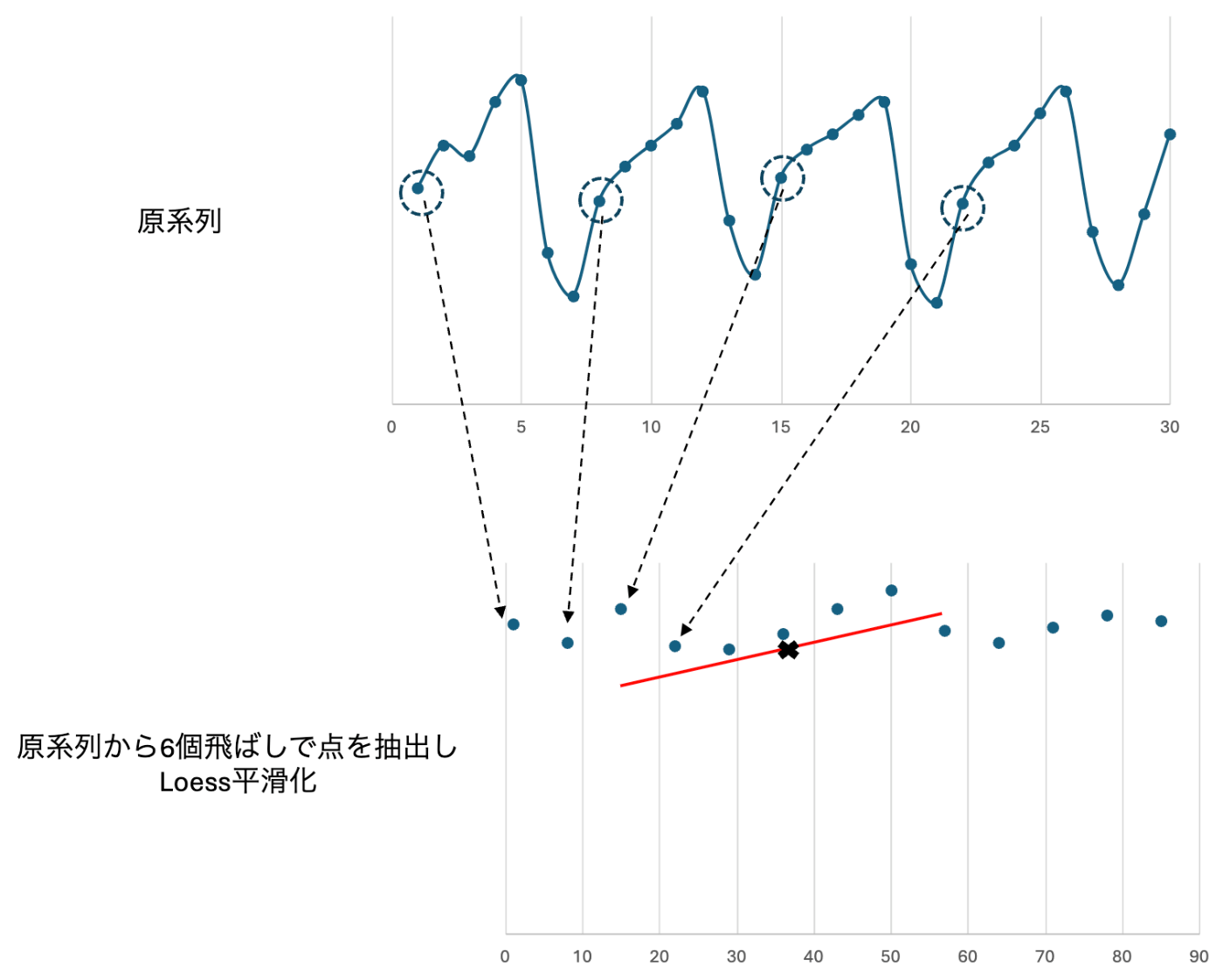
inner loopの手順2「周期成分の平滑化」では、以下手順で平滑化を行います。

  1. 事前に設定したパラメータ「季節性の周期の長さ」ごとに、原系列から点を抽出
  2. 抽出したデータに対して、Loess平滑化

例えば、日次データから曜日成分を分解する場合、曜日ごとに(6個飛ばし)点を抽出し、Loess平滑化を行います。

4. STLのパラメータ

Pythonの統計モデルライブラリstatsmodelsでは、statsmodels.tsa.seaasonal.STL[2]クラスを用いてSTLを実行できます。

4.1 statsmodels.tsa.seaasonal.STLクラスのパラメータ

  • period
    季節性の周期の長さ。例えば、月次データから年次成分を分解したい場合は12を指定します。

  • seasonal
    季節性をLoess平滑化する際のウィンドウサイズ。

  • trend
    トレンドをLoess平滑化する際のウィンドウサイズ。

  • low_pass
    ローパスフィルタをLoess平滑化する際のウィンドウサイズ。

  • seasonal_deg
    季節性をLoess平滑化する際の次数。

  • trend_deg
    トレンドをLoess平滑化する際の次数。

  • low_pass_deg
    ローパスフィルタで抽出した低周波成分をLoess平滑化する際の次数。

  • robust
    ロバスト重みを使用するかどうかを指定するフラグ。

  • seasonal_jump
    季節性をLoess平滑化する際のスキップ値。seasonal_jump=1とすると全ての点に対して平滑化値を計算し、2とすると1つ飛ばしで平滑化値を計算します。飛ばされた点は、前後の点から線形補間されます。大きな値を設定すると、平滑化値を計算する点が減るため、処理時間が短縮されます。

  • trend_jump
    トレンドをLoess平滑化する際のスキップ値。

  • low_pass_jump
    ローパスフィルタで抽出した低周波成分をLoess平滑化する際のスキップ値。

4.2 fit[3]メソッドのパラメータ

  • inner_iter
    inner loopの反復回数。
  • outer_iter
    outer loopの反復回数。

5. STLの拡張

本記事では、時系列データを「トレンド」「季節性」「残差」に分解する手法であるSTLについて解説しました。しかし、STLは単一の季節性しか扱えないため、複数の季節性を持つ時系列データに対しては十分な分解性能を発揮できません。
この課題を解決するために、STLを拡張したMSTLという手法が考案されています。MSTLを用いることで、時系列データを「トレンド」「複数の季節性」「残差」に分解することができます。
MSTLの詳細については、以下記事で解説しているので、ぜひご参照ください。

脚注

  1. Robert B. Cleveland, William S. Cleveland, Jeam E. McRae, and Irma Terpenning. 'STL: A Seasonal-Trend Decomposition Procedure Based on LOESS', Journal of Official Statistics, vol6, No.1, pp.3-73, (1990) ↩︎

  2. statsmodels.tsa.seasonal.STL ↩︎

  3. statsmodels.tsa.seasonal.STL.fit ↩︎

Discussion