Zenn
🤹‍♂️

MSTLの仕組みを理解してパラメータを適切に設定する【Python】【statsmodels】

2024/11/05に公開
Python
時系列
時系列分析
statsmodels
tech

1. 概要

本記事の目的

本記事では、時系列データを「トレンド」「季節性」「残差」の3要素に分解するSTL[1](Seasonal Trend decomposition using Loess)を拡張し、複数の季節性を持つ時系列データを処理できるようにしたMSTL[2](Multiple STL)について解説します。
MSTLのアルゴリズムを理解し、適切なパラメータ設定を行えるようになることを目指します。

MSTLの概要

まず、MSTLの基礎となるSTLについて簡単に説明します。STLは時系列データを以下の3要素に分解する手法です。

  • トレンド(Trend)
    時系列の長期的な傾向
  • 季節性(Seasonal)
    一定期間で繰り返す周期的な変動(例: 日、週、月、年)
    「季節性の周期の長さ」は事前にパラメータで設定
  • 残差(Remainder)
    トレンドや季節性で説明できない、不規則な変動成分

STLのアルゴリズム・パラメータについては、以下記事を参照してください。

MSTLはSTLを拡張した手法で、時系列データをトレンド・複数の季節性・残差に分解できるようにした手法です。

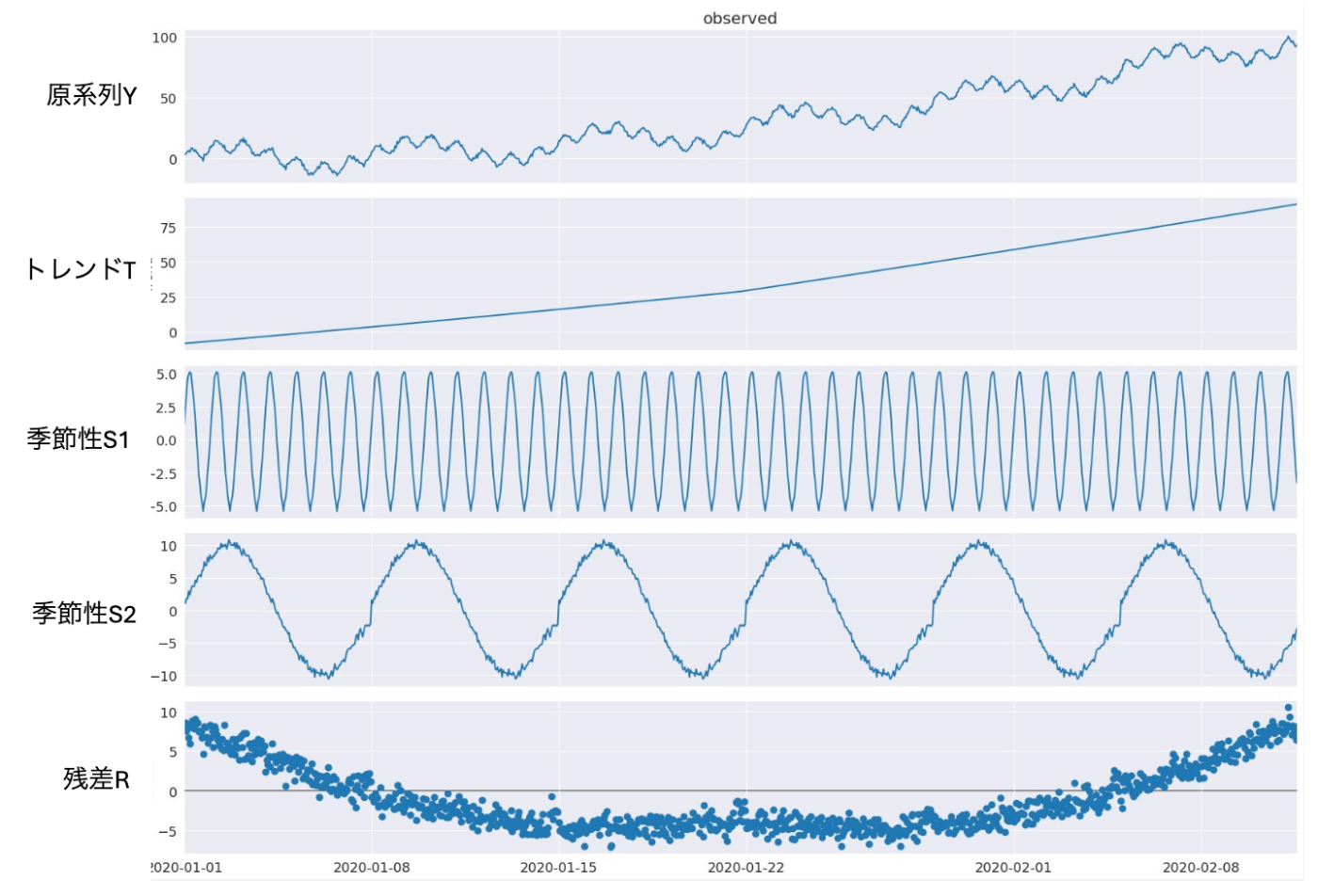
本記事では、2章でMSTLのアルゴリズム、3章でstatsmodelsのMSTLのパラメータについて解説します。

2. MSTLのアルゴリズム

MSTLは前処理->成分分解->後処理の順に処理を行います。

前処理

1. パラメータ「季節性の周期の長さ」を決定

時系列データに含まれる可能性がある季節性を特定し、それぞれの周期を設定します。

例) 年次、週次の季節性がある日別データの場合
季節性の周期の長さは[365, 7]となります。

2. 分解対象の季節性を周期の長さでフィルタリング

1で特定した季節性候補のうち、原系列の長さの半分以上の周期をもつ季節性を除外します。ランダムな変動と区別が難しいためです。

例)1年分(365日分)の日別データの場合
周期の長さが365/2=182.5以上の季節性は除外

3. パラメータ「季節性の周期の長さ」を昇順にソート

季節性の分解は、パラメータ「季節性の周期の長さ」の格納順で行われます。そのため、周期の長さの昇順(短い順)にソートしておきます。周期が長い季節性を先に分解すると、短い季節性が吸収される可能性があるためです。

4. 欠損値を補完

正確な分解のために、データの欠損値を補完します。

5. Box-Cox変換

データを正規分布に近づけるための手法で、時系列データを定常化します。特に、\lambda=0のBox-Cox変換は、対数変換となります。

\begin{equation} Z_{n} = \begin{cases} \frac{y^{\lambda}_{n} - 1}{\lambda} & \lambda \neq 0 \\ log y_{n} & \lambda = 0 \end{cases} \end{equation}

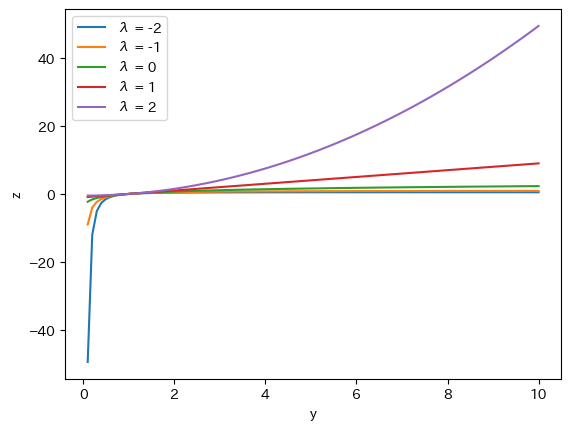
box-cox変換の実装コード
import numpy as np
import matplotlib.pyplot as plt

y = np.linspace(0.1, 10, 100)

fig, ax = plt.subplots()

for lam in [-2, -1, 0, 1, 2]:
    if lam == 0:
        z = np.log(y)
    else:
        z = (y**lam - 1) / lam
    ax.plot(y, z, label=f'λ = {lam}')

ax.set_xlabel('y')
ax.set_ylabel('z')
ax.legend()

plt.show()

成分分解

時系列が季節性を持つかどうかで、別の処理を行います。

季節性がある時系列

各季節性に対して、パラメータ「iterate」で指定した回数だけSTLを繰り返し、分解の精度を高めます。
以下では、原系列をY、トレンドをT、n個の季節性をS_{i}(i=1 \sim n)、残差をRとします。季節性は前処理の手順3で昇順にソートされているため、iが小さいほど周期が短くなります。また、j回目(j=1 \sim iterate)のSTLで計算された季節性をS_{i}^{(j)}とします。

1. 各季節性に対して1.1~1.3を実行

以下では、j回目の分解手順を説明します。

  • 1.1 前ループで分解された季節性を加えた系列を生成する
    全ての季節性が除かれた系列(deseas)に、前ループで分解された季節性S_{i}^{(j-1)}を加えます。
\begin{equation} deseas + S_{i}^{(j-1)} \end{equation}
  • 1.2. STLを実行
    1.1で生成した系列に対してSTLを実行し、季節性S_{i}^{(j)}を分解します。
\begin{equation} S_{i}^{(j)} = STL(deseas + S_{i}^{(j-1)}).seasonality \end{equation}
  • 1.3. 新しく分解された季節成分を1.1の系列から引きます
\begin{equation} deseas = deseas + S_{i}^{(j-1)} - S_{i}^{(j)} \end{equation}

2. 手順1をパラメータ「iterate」で指定した回数繰り返し

パラメータで指定された回数だけ、手順1を繰り返し、季節性の精度を高めます。

3. 最後のSTLで抽出されたトレンドをMSTLのトレンドとする

j=iterate回目に、最長周期の季節性S_{n}に対するSTLで抽出されたトレンドをMSTLのトレンドとします。

\begin{equation} T = STL(deseas + S_{n}^{(iterate-1)}).trend \end{equation}

季節性がない時系列

局所回帰に基づいたsupersmoother[3]という平滑化手法を原系列に適用することで、トレンドを抽出します。

後処理

原系列からトレンド、季節成分を除いたデータを残差とします。

\begin{equation} R = Y - T - S_{1} - S_{2} - ... - S_{n} \end{equation}

3. MSTLのパラメータ

Pythonの統計モデルライブラリstatsmodelsでは、statsmodels.tsa.seaasonal.MSTL[4]クラスを用いてMSTLを実行できます。

statsmodels.tsa.seaasonal.MSTLクラスのパラメータ

  • periods
    季節性の周期の長さ。季節性の数だけ設定します。例えば、日次データから週次成分を抽出したい場合は、7を指定します。

  • windows
    季節性をLoess平滑化する際のウィンドウサイズ。季節性の数だけ設定します。STLではseasonalで設定されていました。

  • lmbda
    Box-Cox変換のパラメータ\lambda。

  • iterate
    STLの反復回数。

  • stl_kwargs
    内部で呼び出しているstatsmodels.tsa.seaasonal.STL[5]へ渡すパラメータ。

脚注

  1. Robert B. Cleveland, William S. Cleveland, Jeam E. McRae, and Irma Terpenning. 'STL: A Seasonal-Trend Decomposition Procedure Based on LOESS', Journal of Official Statistics, vol6, No.1, pp.3-73, (1990) ↩︎

  2. Kasun Bandaraa, Rob J. Hyndmanb, and Christoph Bergmeir. 'MSTL: A Seasonal-Trend Decomposition Algorithm for Time Series with Multiple Seasonal Patterns', arXive preprint arXive:2107.13462, (2021) ↩︎

  3. J. H. Friedman, 'A Variable Span Smoother', Stanford University Technical Report No.5(1984) ↩︎

  4. statsmodels.tsa.seasonal.MSTL ↩︎

  5. statsmodels.tsa.seasonal.STL ↩︎

Discussion