🤳
ラドン変換とは？

2025/04/11に公開
今回は、フーリエ変換の親戚のような変換であるラドン変換(Radon transform)について解説していこうと思います。

 Radon変換とは？Radon変換は、CTスキャナーなどの分野で使われる、数学的な手法です。物体に対して角度\thetaの方向からスキャン(数学的には積分)をして、その値を新しい座標にマッピングします。


IMACEL ACADEMY CTの原理①～ラドン変換～より引用

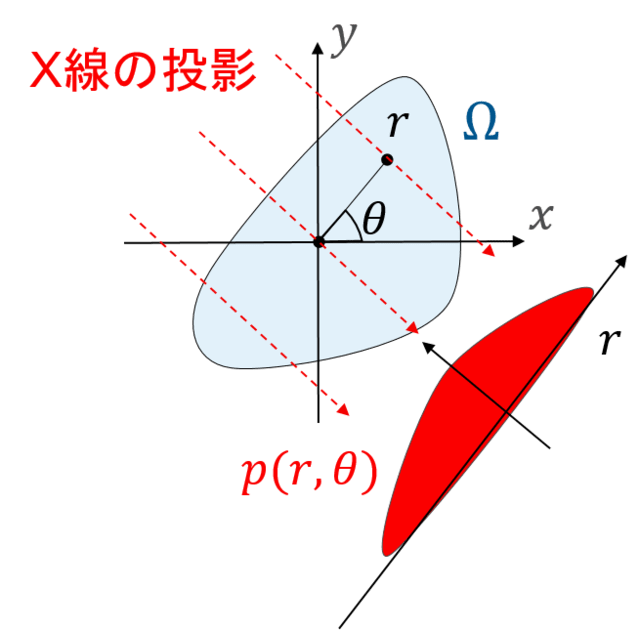
 数学的な定式化以下のように原点を含む領域\Omega = \{(x, y); \, (x, y) \in f(x,y) \geq 0 \}があるとします。CTスキャンの立場では、この領域に物体があると思ってください。



この領域を\theta方向のs軸方向に投影したものが、g(s, \theta)であり、f(x,y)のRadon変換です。

つまり、g(s, \theta)は、\theta方向の法線方向であるような直線で積分し、それをさらにsで積分することにより求まります。
何のこっちゃだと思うので、原点について、g(0,\theta)を求めてみましょう。
まず、\thetaとx, yの関係性を明らかにします。偏角\thetaに対する法線の傾きは\theta + \pi/2であるので、法線方向の直線について、以下が成り立ちます。

\frac{y}{x} = \tan(\theta + \frac{\pi}{2}) = \frac{-\cos \theta}{\sin \theta}
少し、整理してあげて、

x \cos \theta + y \sin \theta = 0 \tag{1}
となります。

この直線に沿って積分するとは、(1)式を満たすような条件で積分してあげれば良いのでdelta関数を用いてg(0,\theta)は以下のように表現できます。

g(0, \theta) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x, y) \delta(x \cos \theta + y \sin \theta)\mathrm{d}x\mathrm{d}y
何となく掴めたでしょうか？今度は偏角\thetaに沿って、sだけ進んだ点について考えてあげると、以下のような式を満たしていれば良いことがわかります。

x \cos \theta + y \sin \theta - s = 0
よって、g(s, \theta)は、

g(s, \theta) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x, y) \delta(x \cos \theta + y \sin \theta - s)\mathrm{d}x\mathrm{d}y\tag{2}
となります。このことをRadon変換と呼ぶこともあるそうです。ただ、\thetaは固定していて線に沿った積分と言っているのに、2重積分をしているのはあまり心地よくありません。そのため、x, yに対して極座標変換を考えます。

\begin{align*}
    \begin{pmatrix}
    s\\
    t
\end{pmatrix}
&= 
\begin{pmatrix}
    \cos \theta & \sin \theta\\
    - \sin \theta & \cos \theta
\end{pmatrix}
\begin{pmatrix}
    x\\
    y
\end{pmatrix}
\end{align*}
これを展開することにより、以下の式が得られます。

\begin{cases}
    s = x\cos\theta + y\sin\theta \\
    t = -x\sin\theta + y\cos\theta
\end{cases}
逆変換は、

\begin{cases}
x = s\cos\theta - t\sin\theta \\
y = s\sin\theta + t\cos\theta
\end{cases}
となります。ヤコビアンを考えてあげると、

\mathrm{d}x\mathrm{d}y = \mathrm{d} s \mathrm{d} t
となるので、(2)はs,tを用いて以下のように変形できます。

g(s, \theta) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f( s\cos\theta - t\sin\theta ,s\sin\theta + t\cos\theta ) \delta(s - s)\mathrm{d}s\mathrm{d}t
ここで、デルタ関数の中身を見てみると0となりますが、これはsについての積分は潰れている、しなくて良いということです。よって、さらに計算する事ができ、

(\text{RHS}) = \int_{-\infty}^{\infty}f( s\cos\theta - t\sin\theta ,s\sin\theta + t\cos\theta )\mathrm{d}t
これがRadon変換です。フーリエ変換のように、以下のように表現します。

\mathscr{R}f(s, \theta) \coloneqq \int_{-\infty}^{\infty}f( s\cos\theta - t\sin\theta ,s\sin\theta + t\cos\theta )\mathrm{d}t
次は、このRadon変換を用いて、フーリエスライスの定理を証明したいと思います。
Radon変換とは？

数学的な定式化

Discussion
