機械学習において、データ点をユークリッド空間でない空間(多様体)に埋め込むことで精度が向上することがあります。その中の1つが、2017年にFacebook(Meta)のグループから報告されたPoincaré embeddingです。Poincaré embeddingでは、双曲幾何のモデルの一つであるPoincaré diskにデータを埋め込みます。
Poincaré disk上の2点 x, y 間の距離 d(x, y) は
\begin{align}
d(x, y) = \cosh^{-1} \left(
1 + \frac{2 \|x - y\|^2}{(1 - \|x\|^2)(1 - \|y\|^2)}
\right)
\end{align}
ですが、どこからこの複雑な式が出てきたのでしょうか。今回はこれを求めてみます。
計量、長さ、距離
Poincaré disk上の距離がユークリッド距離と異なるのは、Poincaré diskとユークリッド空間とで計量が異なる事に起因しています。
計量は、2つのベクトルの内積を決める因子(2階対称テンソル)です。ベクトル空間 V における内積とは、以下の性質を持つ写像 g:V \times V \to \R の事です。
- g(u, v) = g(v,u)
-
u,v,w \in V, a \in \R について g(au+v,w) = a g(u,w) + g(v,w)
- 任意の v \in V について g(u,v) = 0 \Longrightarrow u = 0
性質2 (双線形性) から、基底同士の内積が決まればあらゆるベクトル同士の内積の値が自動的に決まります。V の基底 \{e_1,e_2,\cdots,e_n\} に対して、
とします。x, y \in V を基底で展開すると x = \sum_{i=1}^n x^i e_i, y = \sum_{i=1}^n y^i e_i となるため、これらの内積は
\begin{align}
g(x,y) &= g \left(
\sum_{i=1}^n x^i e_i,
\sum_{j=1}^n y^j e_j
\right) \nonumber \\
&= \sum_{i=1}^n \sum_{j=1}^n
x^i y^j g(e_i,e_j)
\nonumber \\
&= \sum_{i=1}^n \sum_{j=1}^n
g_{ij} x^i y^j
\end{align}
と表せます。
ベクトル x の大きさ (ノルム) \|x\| = \sqrt{g(x, x)} で定義します。ベクトルの微小変位 \mathrm{d}x = (\mathrm{d}x^1, \mathrm{d}x^2, \cdots, \mathrm{d}x^n) の大きさ \mathrm{d}s を用いて、曲線 C の長さ L[C] を定義できます。
L[C] = \int_C \mathrm{d}s = \int_C \sqrt{g_{ij} \mathrm{d}x^i \mathrm{d}x^j}
C の端点を a, b とすると、L[C] が最小となる C (最短経路) の長さが a, b 間の距離になります。
また、ベクトル x, y のなす角 \phi は \cos \phi = \dfrac{g(x, y)}{\|x\| \|y\|} で定義されます。以上より、内積は距離や角度といった空間の性質を決めると言えます。
ユークリッド空間は、標準基底に対して計量
g_{ij} = \delta_{ij} =
\begin{cases}
1 & i = j \\
0 & i \neq j \\
\end{cases}
が入った空間と言えます。
双曲幾何のモデル
双曲幾何には計量 \{g_{ij}\} の異なる複数のモデルが知られています。
上で紹介したPoincaré disk \mathbb{D}^n は n 次元の単位開球 \mathbb{D}^n = \{x \in \R^n\ |\ \|x\| < 1\} であり、以下の計量
g_{ij} = \left(
\frac{2}{(1 - \|x\|^2)}
\right)^2
\delta_{ij}
(Poincaré 計量)が入っています。
別のモデルとして双曲面(hyperboloid)があります。\R^{n+1} の基底 \{e_0, e_1, \cdots, e_n\} に対して
g_{ij} = \eta_{ij} = \begin{cases}
-1 & i = j = 0 \\
1 & i = j = 1, 2, \cdots, n \\
0 & \text{otherwise}
\end{cases}
をミンコフスキー計量と呼びます。
p = (p^0,p^1,\cdots,p^n), q = (q^0,q^1,\cdots,q^n) \in \R^{n+1} 間のミンコフスキー内積を
\begin{align}
\langle p,q \rangle_\Bbb{H} \coloneqq
\sum_{i=1}^n \sum_{j=1}^n
\eta_{ij} p^i q^j
= -p^0 q^0 + \sum_{i=1}^n p^i q^i
\end{align}
と表記します。
\langle p,p \rangle_\mathbb{H} = -1 が満たす点の集合を二葉双曲面と呼びます。二葉双曲面は p^0 の符号により2つの部分空間に分かれます。p^0 > 0 の双曲面を \mathbb{H}^n とします。つまり \mathbb{H}^n = \{p \in \R^{n+1}\ |\ \langle p,p \rangle_\mathbb{H} = -1, p^0 > 0\} です (下図の青い部分)。これにミンコフスキー計量を入れたものは双曲幾何のモデルになります。
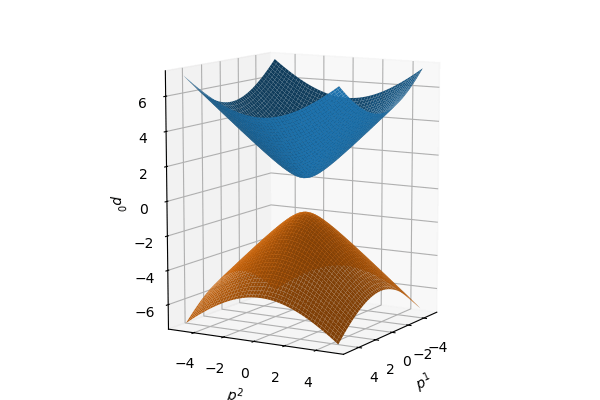
双曲面モデルにおける距離
2点間の距離を求めるには双曲面モデルの方が簡単なので、こちらから考えてみます。
まず、2点間のミンコフスキー内積が変化しないような線形変換 (ローレンツ変換) を考えます。
ローレンツ変換
\R^{n+1} におけるローレンツ変換は、
\begin{align}
\Lambda^T \eta \Lambda = \eta
\end{align}
を満たす (n+1) \times (n+1) 行列 \Lambda で表せます。ここで \eta は (i,j) 成分に \eta_{ij} を持つ行列です。
ミンコフスキー内積を変えないので、ローレンツ変換は2点間の距離を保つ変換 (等長変換)です。従って、双曲面モデルにおける距離を求める際、
- ローレンツ変換を用いて、計算が容易な位置に2点を移動 (例えばどちらかを原点に移動)
- 2点間の距離を求めた後、別のローレンツ変換を用いて元に戻す
ことができれば計算が簡単になりそうです。そのためには、ローレンツ変換でどこでも自由に行けること、つまり
-
\Bbb{H}^n 上の任意の2点 p,q について、p を q に写すローレンツ変換が必ず存在する(推移的)
ことが保証されている必要があります。
まず、ローレンツ変換のうち\Bbb{H}^n を \Bbb{H}^n に写すもの (*) を考えます。全てのローレンツ変換が当てはまる訳ではなく、例えば p^0 の符号を反転させる変換はローレンツ変換ですが、変換先は \Bbb{H}^n から外れます。(*) を満たすローレンツ変換を特に順時ローレンツ変換と呼びます。
例えば、p^0 軸に関する回転行列
R_0 =
\begin{pmatrix}
1 & 0 \\ 0 & R
\end{pmatrix}
は順時ローレンツ変換です。ただし、R は n \times n の直交行列で \det R = 1 です。R^T R = I より、R_0^T \eta R_0 = \eta となります。
また、p = (p^0,p^1,\cdots,p^n) = (p^0,\overrightarrow{p}) を o = (1,0,\cdots,0) に写す順時ローレンツ変換 \Lambda_{p \to o} は、
\Lambda_{p \to o} =
\begin{pmatrix}
p^0 & -\overrightarrow{p}^T \\ -\overrightarrow{p} & I_n + \frac{p^0 - 1}{\|\overrightarrow{p}\|^2}
\overrightarrow{p}\ \overrightarrow{p}^T
\end{pmatrix}
で表せます。確かに \Lambda_{p \to o}p = o となり、かつ p に依らず (2) 式を満たします。
逆変換については、
\Lambda_{o \to p} =
\begin{pmatrix}
p^0 & \overrightarrow{p}^T \\ \overrightarrow{p} & I_n + \frac{p^0 - 1}{\|\overrightarrow{p}\|^2}
\overrightarrow{p}\ \overrightarrow{p}^T
\end{pmatrix}
とすると、 \Lambda_{o \to p}o = p となり、かつ (2) 式を満たします。
2つのローレンツ変換 \Lambda,\Lambda' の積が (\Lambda\Lambda')^T \eta \Lambda\Lambda' = \Lambda'\Lambda\eta\Lambda\Lambda' = \Lambda'\eta\Lambda' = \eta となることから、ローレンツ変換の合成 (積) もローレンツ変換になります。
以上から、\Lambda_{p \to q} \coloneqq \Lambda_{p \to o} \Lambda_{o \to q} とすることで、任意の p を q に写す順時ローレンツ変換を構成できます。これで、順時ローレンツ変換の推移性を示せました。
距離の導出
では、2点 p,q \in \Bbb{H}^n の距離 d_\Bbb{H} (p, q) を導出します。
p と q を結ぶ曲線を \gamma: [0,1] \to \Bbb{H}^n, t \mapsto \gamma(t) とします。\gamma(0) = p, \gamma(1) = q です。
\gamma の長さを L[\gamma] とします。\Bbb{H}^n にはミンコフスキー計量が入っているので、
L[\gamma] = \int_0^1 \mathrm{d}s
= \int_0^1 \mathrm{d}t \sqrt{\langle \dot{\gamma}, \dot{\gamma} \rangle_\Bbb{H}}
となります。ただし \dot{\gamma} \coloneqq \dfrac{d\gamma}{dt} です。
L[\gamma] が最小になるような \gamma の長さが p, q 間の距離となります。
簡単のため、\Bbb{H}^2 とします。
まず、p,q を \Lambda_{p \to o} で写した点を p',q' \in \Bbb{H}^2 とします。p' = o = (1,0,0) です。q' = (q^0,q^1,q^2) はパラメータ \theta, \phi を用いて以下のように書けます。
\begin{align}
q^0 &= \cosh \theta \nonumber \\
q^1 &= \sinh \theta \sin \phi \nonumber \\
q^2 &= \sinh \theta \cos \phi \nonumber \\
\end{align}
\cosh^2 \theta - \sinh^2 \theta = 1, \sin^2 \phi + \cos^2 \phi = 1 より、\langle q',q' \rangle_\mathbb{H} = -1 を満たします。
更に、p^0 軸に関する回転行列 R_0 を用いて、q' \mapsto q'' = (\cosh \theta, \sinh \theta, 0) に写します。この変換によってp' は動かないため、p'' = (1,0,0) です。
従って、p'' と q'' を結ぶ曲線 \gamma: [0,1] \to \Bbb{H}^2 は、\theta を t の単調増加関数として
\gamma(t) = (\cosh \theta(t), \sinh \theta(t), 0),
\hspace{0.3in}
\gamma(0) = p'', \gamma(1) = q''
と表せます。\dot{\gamma} = (\sinh \theta(t) \dot{\theta}, \cosh \theta(t) \dot{\theta}, 0) より、
L[\gamma]
= \int_0^1 \mathrm{d}t \sqrt{\langle \dot{\gamma}, \dot{\gamma} \rangle_\Bbb{H}}
= \int_0^1 \mathrm{d}t \sqrt{
\dot{\theta}^2 (-\sinh^2 \theta + \cosh^2 \theta)
}
= \int_0^1 \mathrm{d}t \sqrt{\dot{\theta}^2}
となります。この最小値が p'',q'' 間の距離 d_\Bbb{H}(p'',q'') です。
次に、L[\gamma] が最小になるときの \theta(t) を求めます。そのために、\theta(0) = 0, \theta(1) = \theta の条件で以下のオイラー=ラグランジュ方程式を解きます。
\frac{\partial E}{\partial \theta} -
\frac{\mathrm{d}}{\mathrm{d}t}
\left(\frac{\partial E}{\partial \dot{\theta}} \right) = 0,
\hspace{0.3in}
E = \sqrt{\dot{\theta}^2}
\dfrac{\partial E}{\partial \theta} = 0, \dfrac{\partial E}{\partial \dot{\theta}} = \dfrac{\dot{\theta}}{\sqrt{\dot{\theta}^2}} より、
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}
\left(\dfrac{\dot{\theta}}{\sqrt{\dot{\theta}^2}} \right) &= 0 \\
\frac{\dot{\theta}}{\sqrt{\dot{\theta}^2}} &= C_0 \\
\dot{\theta} &= C_1 \\
\therefore
\theta(t) &= C_1t + C_2
\end{align*}
\theta(0) = 0, \theta(1) = \theta より、C_1 = \theta, C_2 = 0 となり、\theta(t) = \theta、つまり \theta を 0 から直線的に変化させるのが最短経路という事が分かりました。
パラメータを \theta \to t に付け替えて、
d_\Bbb{H}(p'',q'') = \int_0^\theta \mathrm{d}t \sqrt{\langle \dot{\gamma}, \dot{\gamma} \rangle_\Bbb{H}}
= \int_0^\theta \mathrm{d}t \sqrt{-\sinh^2 t + \cosh^2 t}
= \int_0^\theta \mathrm{d}t = \theta
となります。ローレンツ変換により距離及び内積は不変なので、
\begin{align*}
d_\Bbb{H}(p'',q'') &= d_\Bbb{H} (p, q) = t \\
\langle p'',q'' \rangle_\Bbb{H} &=
\langle p,q \rangle_\Bbb{H} = -\cosh t
\end{align*}
です。従って、p,q間の距離は
\begin{align}
d_\Bbb{H} (p, q) = \cosh^{-1}(-\langle p,q \rangle_\Bbb{H})
\end{align}
となることが分かりました。
Poincaré diskにおける距離
Poincaré diskと双曲面モデルの関係
Poincaré disk \Bbb{D}^n は双曲面モデル \Bbb{H}^n の「立体射影」です。\Bbb{H}^n 上の点 p = (p^0,p^1,\cdots,p^n) と、(-1,0,\cdots,0) と結ぶ直線を \ell とし、p^0 軸に垂直かつ原点を通る (超) 平面 E と \ell の交点を \hat{x} = (0,x^1,\cdots,x^n) とします。p から \hat{x} への変換 \phi は、
x^i = \frac{p^i}{1+p^0},
\hspace{0.2in}
i=1,2,\cdots,n
と表せます。
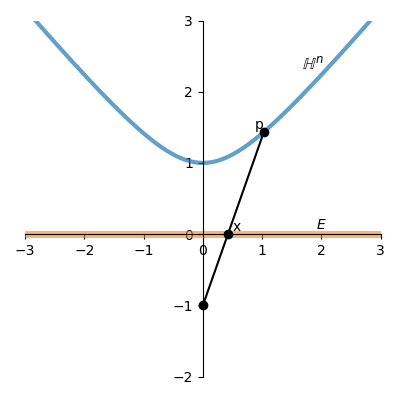
-(p^0)^2 + \sum_{i=1}^n (p^i)^2 = -1 より、
\|x\|^2 = \frac{(p^0)^2 - 1}{(p^0 + 1)^2}
= \frac{p^0 - 1}{p^0 + 1}
となります。p^0 \geqq 1 より 0 \leqq \|x\| < 1 となるため、x は単位開球内の点であることが分かります。これを \R^n 上の点 x = (x^1,\cdots,x^n) と見なしたものがPoincaré disk \Bbb{D}^n です。
距離の導出
上記で定義した \phi: \Bbb{H}^n \to \Bbb{D}^n は等長写像とします。つまり、Poincaré disk上の距離を d_\Bbb{D} とすると、
d_\Bbb{H}(p, q) = d_\Bbb{D}(\phi(p), \phi(q))
です。この関係を使って、Poincaré diskにおける距離 (1) を導出します。
p と x は1対1に対応します (\phi: \Bbb{H}^n \to \Bbb{D}^n は全単射)。従って \phi の逆写像 \phi^{-1}: \Bbb{D}^n \to \Bbb{H}^n が存在します。具体的には、
\begin{align}
p^0 = \frac{1 + \|x\|^2}{1 - \|x\|^2},
\hspace{0.2in}
p^i = \frac{2 x^i}{1 - \|x\|^2}
\hspace{0.2in}
i = 1,2,\cdots,n
\end{align}
です。x, y \in \Bbb{D}^n 間の距離 d_\Bbb{D}(x, y) は
\begin{align*}
d_\Bbb{D}(x, y)
&= d_\Bbb{H}(\phi^{-1}(x), \phi^{-1}(y)) \\
&= \cosh^{-1} (-\langle \phi^{-1}(x), \phi^{-1}(y) \rangle)
\hspace{0.2in}
(\because\ (5)) \\
&= \cosh^{-1}
\left(
\frac{(1 + \|x\|^2)(1 + \|y\|^2)}{(1 - \|x\|^2)(1 - \|y\|^2)} -
\frac{\sum_{i=1}^n 4 x^i y^i}{(1 - \|x\|^2)(1 - \|y\|^2)}
\right)
\hspace{0.2in}
(\because\ (6)) \\
&= \cosh^{-1}
\left(
\frac{1 + \|x\|^2 + \|y\|^2 + \|x\|^2\|y\|^2 - 4 x^T y}
{(1 - \|x\|^2)(1 - \|y\|^2)}
\right)
\\
&= \cosh^{-1}
\left(
\frac{
1 - \|x\|^2 - \|y\|^2 + \|x\|^2\|y\|^2 +
2\|x\|^2 + 2\|y\|^2 - 4 x^T y}
{(1 - \|x\|^2)(1 - \|y\|^2)}
\right)
\\
&= \cosh^{-1}
\left(1 +
\frac{2\|x - y\|^2}
{(1 - \|x\|^2)(1 - \|y\|^2)}
\right)
\end{align*}
となり、(1) 式を導出できました。
まとめ
Poincaré disk上の距離を求めるために、
- 計算の容易な双曲面モデルで距離を考え、
- 等長変換 \phi を用いてPoincaré disk上の点に変換
というステップを踏みました。双曲幾何を用いたデータ点のembeddingにおいて、Poincaré diskは (2, 3次元であれば) 視覚的に分かりやすいですが、距離等の計算は双曲面モデルの方が簡単です。従って、Poincaré embeddingの著者らは、2018年に双曲面モデルへのembeddingの方法を提案しています。
双曲面モデルにおけるミンコフスキー計量を変えない変換はローレンツ変換でした。同様に、Poincaré diskにおけるPoincaré計量を変えない変換はメビウス変換と呼ばれます。メビウス変換は複素平面 (リーマン球面) で定義されますが、それを高次元に拡張したもの (Möbius addition) を用いてPoincaré disk上の最適化を定式化する手法も報告されています。
この文献では、ニューラルネットワークの重みをPoincaré disk上の点を重みとしたニューラルネットワーク (Hyperbolic neural networks) を提案しています。この他にも様々な機械学習の手法において、双曲幾何への置換が試みられています。
参考文献
余談
ローレンツ変換は以下の性質
- ローレンツ変換同士の積もまたローレンツ変換になる
- 恒等変換 (単位行列) もローレンツ変換の条件を満たす
- ローレンツ変換の逆変換 (逆行列) もローレンツ変換となる
を持ちますが、このような性質を持つ集合を群と呼びます。ローレンツ変換全体のなす群をローレンツ群と呼びます。また、上記の3つの性質は順時ローレンツ変換に置き換えても成り立ちます。この事を順時ローレンツ変換のなす群はローレンツ群の部分群である、と言います。
更に余談
Markdownでは、Poincaréの é は é で出ます。

Discussion