PBDの曲げ拘束を実装する (2D)

PBD (Position Based Dynamics) は、物理演算を行う際のアルゴリズムのひとつです。布やヒモ、髪などの変形のある物体の挙動のシミュレーションを行うのによく使われています。

PBDの基本と距離拘束

PBDでヒモをつくる際、ヒモを一連の質点のあつまりとして表現し、質点間の距離が一定になるような拘束条件（距離拘束, distance constraint）を与えます。

処理の流れとしては、以下のような感じです。

• 各質点に外力と速度に基づく位置更新を行う
• 各質点間の距離が一定になるよう、各質点の位置を更新する
• 更新された位置から新しい速度を逆算する
• 以上を1ステップとして繰り返す

PBDの基本的な実装や距離拘束については詳しい記事がすでにたくさんあるので、この記事では省略します。

https://zenn.dev/r_ngtm/articles/position-based-dynamics-string

https://qiita.com/doRA9876/items/0f2c79204f2412c0f7a3

元の論文はこちらです。2006年の論文なんですね……！

https://matthias-research.github.io/pages/publications/posBasedDyn.pdf

曲げ拘束

今日の本題はこっち。

特定の形状に戻ろうとする拘束が曲げ拘束 (bending constraint) です。クセのついたヒモや布、重力に逆らってある程度の硬さで自立する髪や草木なども作れます。

距離拘束が質点間の距離を保とうとする拘束だったのに対し、曲げ拘束は質点における角度を保とうとする拘束になります。

C# (Unity) での実装例はこちらにあります。
https://gist.github.com/ruccho/6526987988fdd1f3cdc4fd0c69ce8964#file-pbdstrip-cs-L239

こちらの実装はSubstep XPBDベースになっているため、最後のほうの計算がこの記事で紹介する方法と異なります。とはいっても途中までは一緒です！

XPBD, Substep XPBDについてはこちらが参考になります：

https://qiita.com/cy-tatsuya-sakai/items/a028f2a639083786a5a0

https://mmacklin.com/smallsteps.pdf

PBDにおける拘束条件の一般化

PBDにおける拘束条件は一般化されているため、まずはそちらを確認してみます。導出まで詳しく知りたい方は元の論文を読んでみてください（自分は半分もわからないのでここでは結果だけ……）

また、PBDの導出を詳細に追っている記事もあります。

https://zenn.dev/nrdev/articles/141dbc5774f666

---

それでは見ていきます。

拘束を適用する質点を $\bold{p}_1, ..., \bold{p}_n$ として、拘束を表す関数を $C$ として表現します。PBDは $C = 0$ に近づくように質点の位置を調整します。

$$C(\bold{p}_1, ..., \bold{p}_n) = 0$$

例えば、距離拘束なら、質点間の理想的な距離を $d$ として、拘束関数はこのように表現されます。

$$C(\bold{p}_1, \bold{p}_2) = |\bold{p}_1 - \bold{p}_2| - d$$

なるほどですね。

---

次に、各ステップにおいて、拘束条件が質点の位置をどのように更新するかです。

$$s = \frac{C(\bold{p}_1, ..., \bold{p}_n)}{\sum_jw_j|\nabla_{\bold{p}_j}C(\bold{p}_1, ..., \bold{p}_n)|^2}$$

$$\Delta \bold{p}_i = -sw_i\nabla_{\bold{p}_i}C(\bold{p}_1, ..., \bold{p}_n)$$

$w_j$ は質点 $j$ の質量の逆数です。位置が固定された質点は無限大の質量をもっているとみなせるので、 $w=0$ として計算できます。

そして、この式では拘束関数の勾配 $\nabla_{\bold{p}_i}C(\bold{p}_1, ..., \bold{p}_n)$ が登場しています。先ほどの距離拘束を例にとると、各質点の勾配はこんな感じ。

$$\nabla_{\bold{p}_1}C(\bold{p}_1, \bold{p}_2) = \frac{\bold{p}_1 - \bold{p}_2}{|\bold{p}_1 - \bold{p}_2|}$$

$$\nabla_{\bold{p}_2}C(\bold{p}_1, \bold{p}_2) = - \frac{\bold{p}_1 - \bold{p}_2}{|\bold{p}_1 - \bold{p}_2|}$$

最終的な $\Delta{\bold{p}}$ はこうなります。

$$\Delta\bold{p}_1=-\frac{w_1}{w_1+w_2}(|\bold{p}_1-\bold{p}_2|-d)\frac{\bold{p}_1-\bold{p}_2}{|\bold{p}1-\bold{p}_2|}$$

$$\Delta\bold{p}_2=+\frac{w_1}{w_1+w_2}(|\bold{p}_1-\bold{p}_2|-d)\frac{\bold{p}_1-\bold{p}_2}{|\bold{p}1-\bold{p}_2|}$$

素直にコードに落とし込めそうな式になりました。

拘束関数を数式で表現できれば、さまざまな拘束を作れる！一般化されていてありがたいですね。

曲げ拘束編

さて、同じことを曲げ拘束でもやればよさそうです。今回は2Dのヒモにおける話に限定します。

距離拘束が隣接する2質点に対する拘束条件だったのに対し、曲げ拘束では3点に対する拘束条件になります。

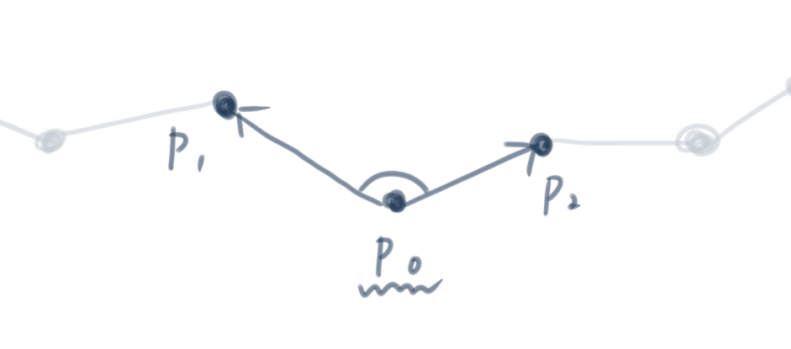
早速ですが、計算の単純化のため、座標系の原点が上の $\bold{p}_0$ にあることにします。最終的な質点位置の更新は $\Delta{\bold{p}}$ によって相対的に行われるので、この座標系の変換はシミュレーションに影響を及ぼしません。

この変換により、$\bold{p}_1$ と $\bold{p}_2$ の座標はそのまま質点間を結ぶベクトルとして扱うことができます。

まずは距離拘束と同じように、拘束関数 $C$ をつくります。 $\bold{p}_1$ と $\bold{p}_2$ のなす角を $\phi_0$ に保つように表現します。

$$C(\bold{p}_0, \bold{p}_1, \bold{p}_2) = \arccos\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right) - \phi_0$$

次に、これを微分して $\nabla C$ を求めます。

$$\begin{aligned} \nabla_{\bold{p}_1}C &= -\frac{1}{\sqrt{1-\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right)^2}} \left( \frac{\partial}{\partial \bold{p}_1} \frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|} \right) \\ &= -\frac{1}{|\bold{p}_1||\bold{p}_2|\sqrt{1-\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right)^2}} \left( \bold{p}_2 - \frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1|^2} \bold{p}_1 \right) \end{aligned}$$

$$\nabla_{\bold{p}_2}C = -\frac{1}{|\bold{p}_1||\bold{p}_2|\sqrt{1-\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right)^2}} \left( \bold{p}_1 - \frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_2|^2} \bold{p}_2 \right)$$

$$\nabla_{\bold{p}_0}C = -\nabla_{\bold{p}_1}C - \nabla_{\bold{p}_2}C$$

式の見通しがよくなく、計算量も減らしたいので、次のように変形しておきます。

$$\nabla_{\bold{p}_i}C = -\frac{1}{|\bold{p}_1||\bold{p}_2|\sqrt{1-\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right)^2}} \bold{q}_i$$

$$\bold{q}_1 = \bold{p}_2 - \frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1|^2} \bold{p}_1$$

$$\bold{q}_2 = \bold{p}_1 - \frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_2|^2} \bold{p}_2$$

$$\bold{q}_0 = - \bold{q}_1 - \bold{q}_2$$

最終的な $\Delta{\bold{p}}$ はこうなります。

$$\Delta \bold{p}_i = -\frac{w_i|\bold{p}_1||\bold{p}_2|\sqrt{1-\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right)^2}\left( \arccos\left(\frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}\right) - \phi_0 \right)}{\sum_jw_j|\bold{q}_j|^2}\bold{q}_i$$

フリップ問題

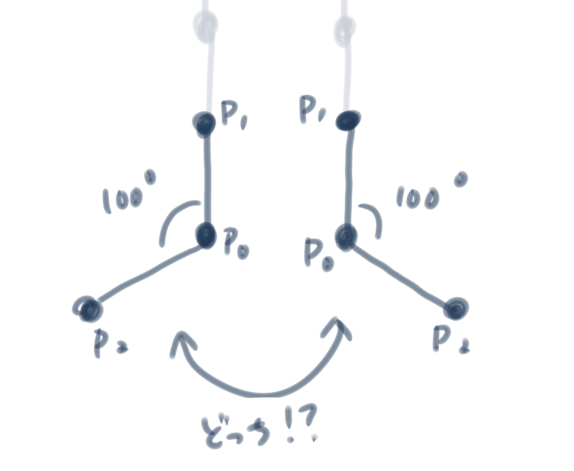
実は上記の式を素直にコードに落とし込んだだけでは不十分です。この拘束条件では、arccosをつかってなす角を求めていますが、$y = \arccos(x)$ の値域は $0 \leq y \leq \pi$ です。
ということは、例えば $\phi_0 = 100\degree$ という条件には、2通りの姿勢があり得ます。

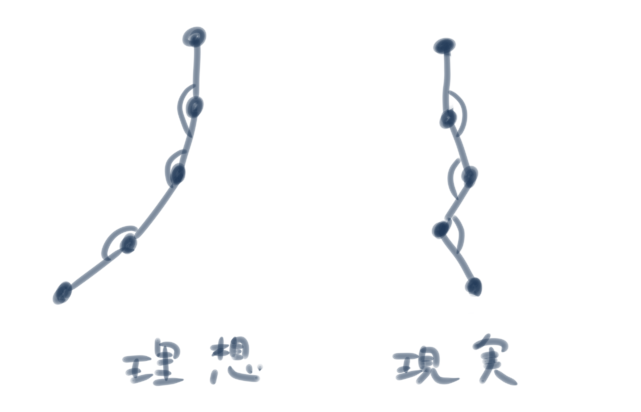
これを解決しないと下のようになります。ゆるやかにカーブしてほしいのに、カクカクになってしまう……

ということで、ちょっと工夫をします。

まずは、ふたつの姿勢を区別します。これは$\bold{p}_1$と$\bold{p}_2$に対して外積の$z$成分 $x_{\bold{p}_1} y_{\bold{p}_2} - y_{\bold{p}_1} x_{\bold{p}_1}$ を計算し、その正負によって区別できます。

これを使って、 $\pi < x < 2\pi$ の範囲も正しく反映されるよう $C$ を修正します。

$$d = \frac{\bold{p}_1 \sdot \bold{p}_2}{|\bold{p}_1||\bold{p}_2|}$$

$$C = \begin{cases} 2\pi - \arccos(d) - \phi_0 & (x_{\bold{p}_1} y_{\bold{p}_2} - y_{\bold{p}_1} x_{\bold{p}_1} > 0)\\ \arccos(d) - \phi_0 & (\text{otherwise}) \end{cases}$$

ということは、$\nabla{C}$ と $\Delta \bold{p}$ も変化します。とはいえほとんど同じです：

$$\Delta \bold{p}_i = \begin{cases} \frac{w_i|\bold{p}_1||\bold{p}_2|\sqrt{1-d^2}\left( 2\pi - \arccos(d) - \phi_0 \right)}{\sum_jw_j|\bold{q}_j|^2}\bold{q}_i & (x_{\bold{p}_1} y_{\bold{p}_2} - y_{\bold{p}_1} x_{\bold{p}_1} > 0)\\ -\frac{w_i|\bold{p}_1||\bold{p}_2|\sqrt{1-d^2}\left( \arccos(d) - \phi_0 \right)}{\sum_jw_j|\bold{q}_j|^2}\bold{q}_i & (\text{otherwise}) \end{cases}$$

これで想像通りの挙動が得られます。

3D（ポリゴン）だとこんな感じらしい

ポリゴンでの詳しい曲げ拘束の導出は、PBDの元論文の末尾 (Appendix A) に記載があります。基本的な考え方はこの記事で紹介したものと同様です。

https://matthias-research.github.io/pages/publications/posBasedDyn.pdf

ポリゴンの場合、曲げ拘束は各辺に着目して、その辺を共有する2つの面がなす角について拘束条件を構築します。2つの面の法線ベクトルを求めるのに外積を使っているため、2Dのときよりも複雑な微分になっているようです。

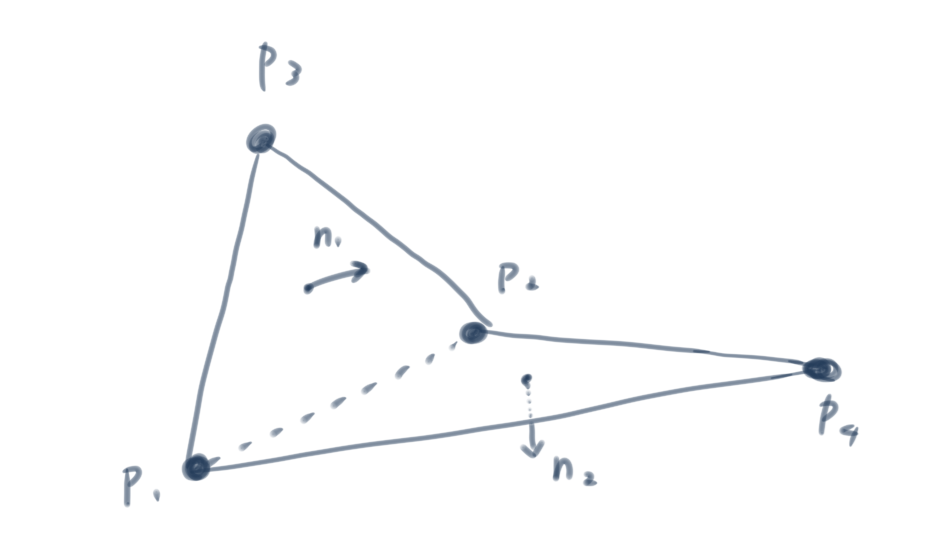
ただ、ポリゴンでもやはりフリップ問題が発生するようで、こちらの動画ではその対処法について言及されていました。自分も2Dでのフリップ問題の解決にこちらの動画を参考にさせていただきました。

https://youtu.be/B-Bakl-VPpg?si=0yv8XqPQFv5TUqBU&t=433