十分統計量とは何ぞや

wikipediaより

• ある統計データに対し、それが従う確率分布を示す母数 θ に対応するその統計量の値が決められた条件下で、データが出現する条件付き確率分布が、もはやθ にはよらない。

教科書には必ず出てくるものの何が重要なのかわからないので、整理を試みてみます。
下記ではすべて離散確率を仮定してます。

数式で書かれた定義

あるパラメータ$\theta$を持つ同一の分布から独立に得られるサンプル列の確率変数${\bf X}$、その統計量を$T({\bf X})$と記述するとして、実際にあるサンプル${\bf x}$が得られ、統計量$t$が計算されるような確率

$$P({\bf X}={\bf x}|T({\bf X})=t)$$

が、分布の持つパラメータ$\theta$に依存しない。

さらにこの定義より次のことがいえる。

$$P({\bf X}={\bf x}|\theta) = P({\bf X}={\bf x}|T({\bf X})=t)P(T({\bf X})=t|\theta)$$

どういうことか

後者の数式について言える大事なことは、十分統計量であるならば、その十分統計量が元の分布のパラメータに依存し、元になったサンプル自体は十分統計量にのみ依存しているものなので、サンプルの情報はすべて十分統計量に入っているということのようです。

グラフィカルに書くと

$$\theta \rightarrow T({\bf X}) \rightarrow {\bf X}$$

という形で影響をしているので、十分統計量が導入されたとき、あくまでサンプルとパラメータとの関係は、十分統計量を通してのみ関係しているために、間接的な関係になります。

つまりサンプル自体を全部持たなくても十分統計量を持つことで元のパラメータに関係のある情報をすべて持てるということになります。（現代数理統計学の基礎 p.117）

統計学的推定において

例えばある平均値を持つガウス分布からi.i.d.なサンプルを得て、平均値を取るとき、それは十分統計量ですが、その十分統計量は最尤推定量でもあります。
つまり、平均値を最尤推定するという点に関して、もはや元のサンプルは必要ではなく、十分統計量さえあればよいということになります。

wikipediaの推計統計学を見ると代表的な統計学的推定方法が三つあります。

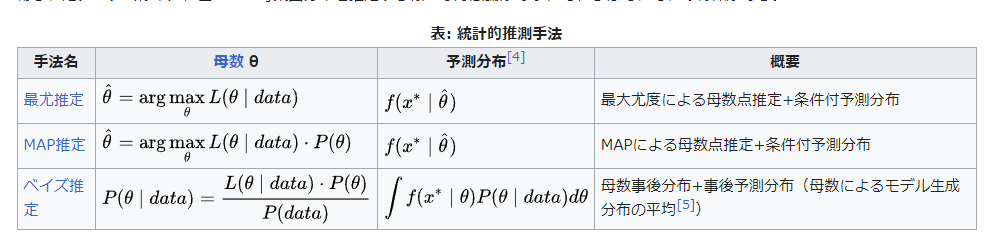
Lは尤度関数なので次のような関係が成り立ちます。

$$P(\theta|{\bf x}) \propto P({\bf x}|t)P(t|\theta)$$

パラメータに関する項以外の項はargmaxにおいては影響しないことを考えると、十分統計量さえあればパラメータの推定においては十分統計量のみあればよいと考えられる。というのが十分統計量の性質のようです。
ベイズ推定においてはどうなんでしょう。共役事前分布のみ扱う変分ベイズなら正規化項に押し込める形で計算できそうですが、一般論としてはよくわかりません。

なお上の式は離散確率を仮定して計算している($P({\bf x}) = P({\bf x}, t)$を利用している)ので、連続の場合はもうちょっと面倒みたいです。周辺化の逆の操作によって出てくるので、連続の場合は$T({\bf x})=t$の領域で積分することが同時確率の密度関数と一致することを示す必要があるためです。（解釈違うかも）