Zenn
💨

機械学習で使う確率・統計の知識を爆速で理解する

2024/03/07に公開
統計
tech

同時確立分布

同時確率分布は、2つ以上の確率変数の組における分布を表すもので、一般的には次のように記述されます。

P(X,Y)

確率分布の定義上、分布の積分値は常に1である必要があります。同時確率分布の場合、次のように2重積分すると値は1となります。
\int \int P(X,Y) dXdY = 1

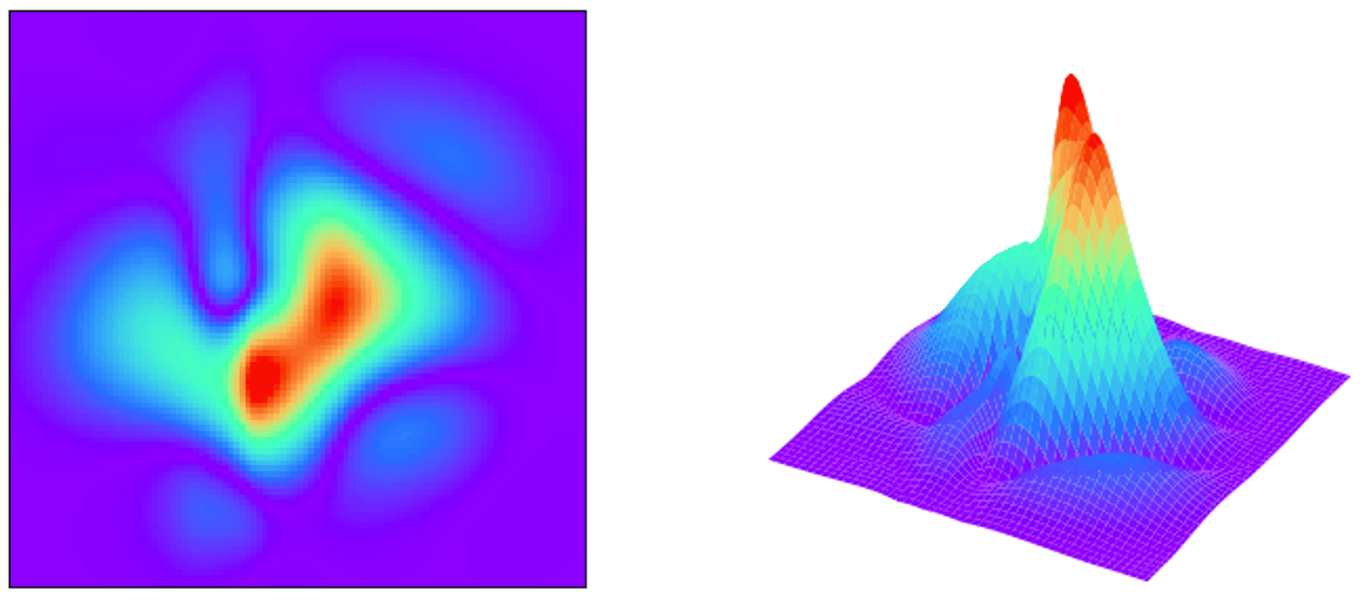
同時確立分布の例。perlin noiseと正規分布を乗算して生成しました。

周辺化・周辺確立分布

周辺化とは、同時確率分布から1つ以上の変数を除去し、残りの変数の確率分布を得る操作を指します。例えば、同時確率分布\mathrm{P}(X, Y)からYを取り除くと、次のようXの確率分布が得られます。

\mathrm{P}(X)=\int \mathrm{P}(X, Y) dY

例えば、Xについて周辺化すると、
P(0) = \int P(0,Y) dY
P(1) = \int P(1,Y) dY
P(2) = \int P(2,Y) dY
：
：
P(X) = \int P(X,Y) dYのようにすべてのXのパターンに対してYについて積分をしています。
P(X) = \int P(X,Y) dY

このような操作をして得られる確率分布を周辺確率分布と呼びます。
以下の図は、Xについての周辺化をした例です。

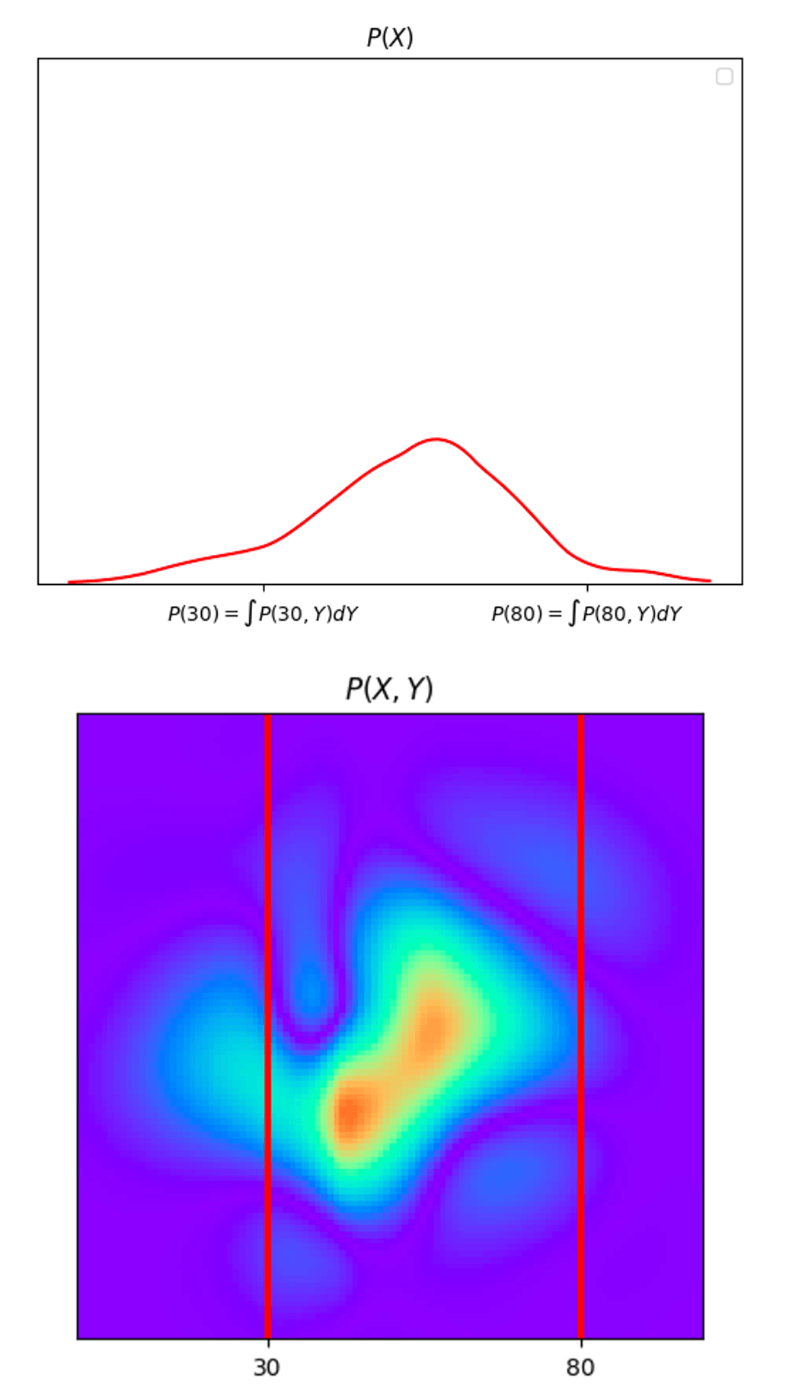
条件付確率

同時確率分布から、特定の条件における分布を切り取ることを考えます。次の画像では、同時確率分布からY=30とY=50の分布を取り出した例が示されています。

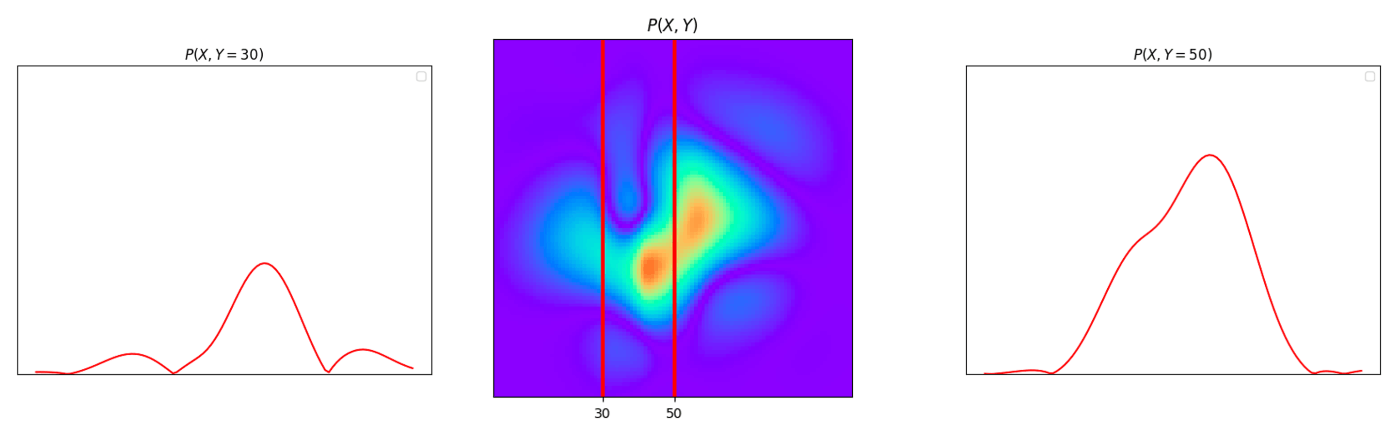
このような場合、取り出した部分は確率密度関数ではありません。同時確率分布は積分値が1であるため確率密度関数ですが、部分的に取り出したものは積分値が1より小さくなります。

これらを確率密度関数に変換するために、正規化を行います。具体的には、以下のように正規化します。

\mathrm{P}\left(X \mid Y=Y^*\right)=\frac{\mathrm{P}\left(X, Y=Y^*\right)}{\int \mathrm{P}\left(X, Y=Y^*\right) d X}=\frac{\mathrm{P}(X, Y)}{\mathrm{P}(Y)}

このようにして正規化された分布を条件付き確率分布と呼びます。

ベイズの定理

ベイズの定理の式

条件付き確率分布の式を変形することで、ベイズの定理を導き出すことができます。基本的な式は次のようになります。

\mathrm{P}(X \mid Y) = \frac{\mathrm{P}(Y \mid X) \mathrm{P}(X)}{ \mathrm{P}(Y)}

また、積分を使った形式もあります。

\mathrm{P}(X \mid Y) = \frac{\mathrm{P}(Y \mid X) \mathrm{P}(X)}{\int \mathrm{P}(Y \mid X) \mathrm{P}(X) dY}

ベイズの定理の意味

上記の式を見ただけでは、ベイズの定理の意味を理解しにくいかもしれません。そこで、この式の右辺の要素について説明します。

右辺の分子の意味

右辺の分子には、以下の2つの要素が含まれます。

  • 事前確率分布: \mathrm{P}(X)は、データを観測する前の確率です。例として、ある国のコインが公正である確率を80%、非公正である確率を20%と仮定します。つまり、事前確率は次のように表されます。

    \mathrm{P}(X = \text{公正}) = 0.8
    \mathrm{P}(X = \text{非公正}) = 0.2

  • 尤度: \mathrm{P}(Y \mid X) は、特定の条件下でデータが観測される確率です。例として、コインを10回投げて6回表が出た場合、公正なコインと非公正なコインの尤度は以下のように計算されます。(非公正なコインの面の出る確立は20%としています)

    \mathrm{P}(Y = 6 \text{表} \mid X = \text{公正}) = \binom{10}{6} \cdot (0.5^6) \cdot (0.5^4) \approx 0.205
    \mathrm{P}(Y = 6 \text{表} \mid X = \text{非公正}) = \binom{10}{6} \cdot (0.2^6) \cdot (0.8^4) \approx 0.01344

この事前確率と尤度を掛け合わせると、データによる確率の補正が行われます。

右辺の分母の意味

分母部分は、正規化を行うための証拠 (Evidence) です。上記の分子部分を計算した後、確率に戻すために次のような正規化が行われます。

\mathrm{P}(Y) = (\mathrm{P}(Y \mid X = \text{公正}) \cdot \mathrm{P}(X = \text{公正})) + (\mathrm{P}(Y \mid X = \text{非公正}) \cdot \mathrm{P}(X = \text{非公正})) \approx 0.166688

この値を用いることで、条件付き確率の証拠として分母を正規化することができます。

ベイズの定理を使った事後確率の計算

事前確率と尤度から、事後確率を計算すると以下のようになります。

  • 公正なコインの事後確率:

    \mathrm{P}(X = \text{公正} \mid Y = 6 \text{表}) \approx \frac{0.205 \cdot 0.8}{0.166688} \approx 0.983

  • 非公正なコインの事後確率:

    \mathrm{P}(X = \text{非公正} \mid Y = 6 \text{表}) \approx \frac{0.01344 \cdot 0.2}{0.166688} \approx 0.017

ベイズの定理の適用例

事前確率では、コインが公正である確率は80%でしたが、10回中6回表が出たことで事後確率が98%になりました。このように、ベイズの定理を使うと、得られたデータに基づいて確率を更新することができます。

結論

この記事では、同時分布からベイズの定理までを解説しました。もし間違いや質問があったら気軽にコメントしてください。

また、最尤推定・MAP推定・ベイズ推定も解説しているので、よかったら以下の記事も読んでみてください。

参照

Discussion