Zenn
📑

【論文メモ】PHASE-AWARE SPEECH ENHANCEMENT WITH DEEP COMPLEX U-NET

2024/04/23に公開
AI
機械学習
論文
音声
音声認識
tech

PHASE-AWARE SPEECH ENHANCEMENT WITH DEEP COMPLEX U-NET

作成日時: 2024年4月19日 9:33
URL: https://openreview.net/pdf?id=SkeRTsAcYm

0.ABSTRACT

  • Cleanの位相を推定は難しいため、今までの音声強調ではNoisyから位相を再利用しつつ、Cleanのスペクトログラムの振幅の推定を行ってきた。

本論文ではその問題を解決するために３つの方法の提案

  1. DCU-Net
  2. 複素数値の極座標単位のマスキング手法
  3. wSDR損失関数
  • これらのモデルは、Voice BankコーパスとDEMANDデータベースの混合物で評価。混合データセットでの削減実験を行い、提案された3つのアプローチが経験的に妥当であることが判明。実験結果は、提案手法がすべてのメトリックで従来のアプローチを大きく上回り、最先端の性能を達成していることを示していた。

1.INTRODUCTION

  • 音声強調は重要だが難しいタスクの１つであり、NoiseとCleanの混ざったNoisyからCleanとNoiseを分離することを目的としている。

  • DNNを使った一般的な手法としては、音源をSTFTしてTF領域（スペクトログラム）に変換して行われる。このスペクトログラムは複素数（実部：振幅、虚部：位相）で表されるので、その両方を推定することが理想的。

  • しかし、位相の推定は難しく振幅のみの推定がされ、位相はNoisyを再利用をしていた。だがSNRが低い場合、Cleanと推定されたCleanの信号の差は大きくなる

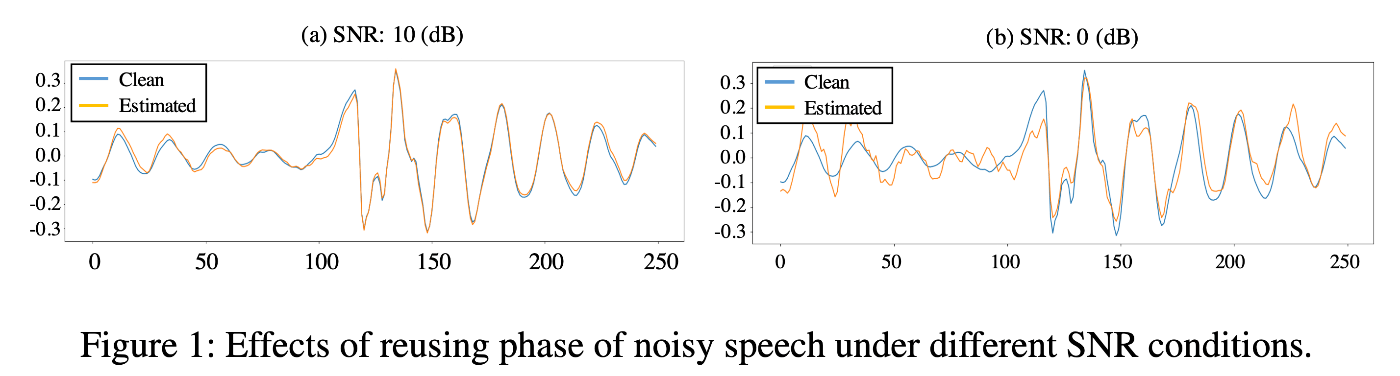
  • 音声強調の一般的なアプローチは、Noisyに適用されるとCleanのスペクトログラムを生成するマスクを最適化すること。

  • 本論文で提案するDCU-Netでは、理想的な複素数値マスクから観察可能な事前知識を用いて極座標で表される複素比マスクを推定するように訓練する。Cleanの複素数値推定を行うことで、スペクトログラムを時系列波形に変換する逆短時間フーリエ変換（ISTFT）を使用することができる。この利点を活かして、多くの音源分離タスクで広く使用されている定量的評価尺度であるソース-歪み比（SDR）を直接最適化する新しい損失関数を導入

つまり、以下のようにまとめられる。

  1. DCU-Netの提案。DCNとU-Netの利点を合わせてSOTAを達成。
  2. 極座標に基づく新しい複素数値マスキング方法を設計
  3. よく知られた定量的評価尺度を直接最適化する新しい損失関数である重み付きSDR損失を提案

3.PHASE-AWARE SPEECH ENHANCEMENT

事前情報

  • Noisy : x(n)=y(n)+z(n) \in \mathbb{R}　→ CleanとNoiseの線形和

    STFT Noisy : Xt,f​∈C

  • Noise : z(n) → ランダムノイズ

    STFT Noise : Zt,f​∈C

  • Clean : y(n) \in \mathbb{R}　→ ノイズのない音源

    STFT Clean : Yt,f​∈C,

  • Est Clean　 : \hat{y}(n) \in \mathbb{R} →Noisyから推定されたClean

    STFT Est : \hat{Y}t,f​∈C,

  • cIRMマスク : Mt,f ∈ C

  • Est Mask : Mt,f ∈ C where M_{t, f}=Y_{t, f} / X_{t, f}

3.1.DEEP COMPLEX U-NET

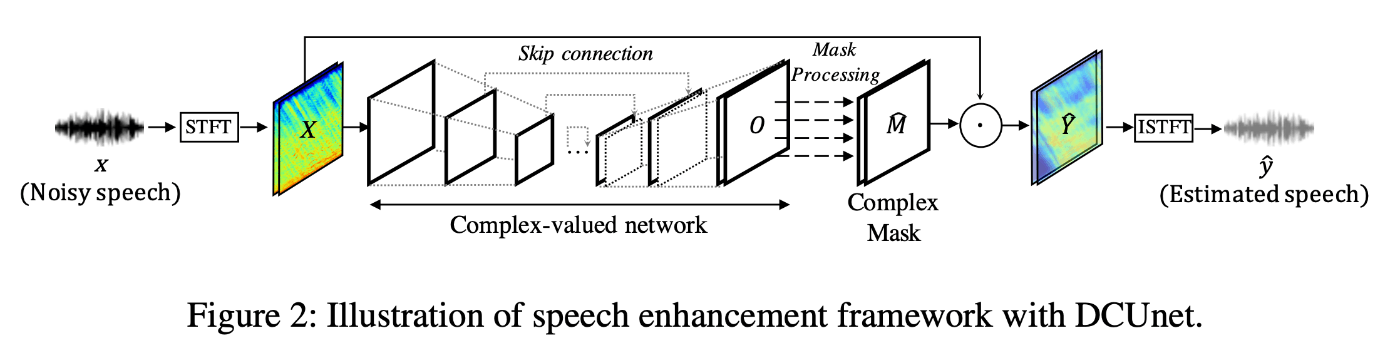
Complex-valued Building Blocks(複素畳み込み)

  • 実数値の行列AとBを持つ複素数値の畳み込みフィルタW = A+iBが与えられた場合、複素数ベクトルh = x + iyに対するWとの複素数値畳み込み操作は、W ∗h = (A∗x−B ∗y)+i(B ∗x+A∗y)で行われる。
  • 実際には、複素数値畳み込みは、共有された実数値の畳み込みフィルタを用いて2つの異なる実数値の畳み込み操作として実装される

Modifying U-Net(DCU-Netの概要).

  • U-Netの畳み込み層を全て複素数値畳み込みに置き換える。カーネルは、一般化および高速学習のために重みテンソルをユニタリ行列として初期化
  • 複素Batch Normは、ネットワークの最後の層を除くすべての畳み込み層に適用される。
  • エンコーディング段階では、空間情報の損失を防ぐために、MaxPoolingはストライドされた複素畳み込み層に置き換え
  • デコーディング段階では、ストライドされた複素数値転置畳み込みを使用して入力のサイズを復元。
  • 活性化関数は、CReLUをLeaky CReLuに変更

3.2 COMPLEX-VALUED MASKING ON POLAR COORDINATES

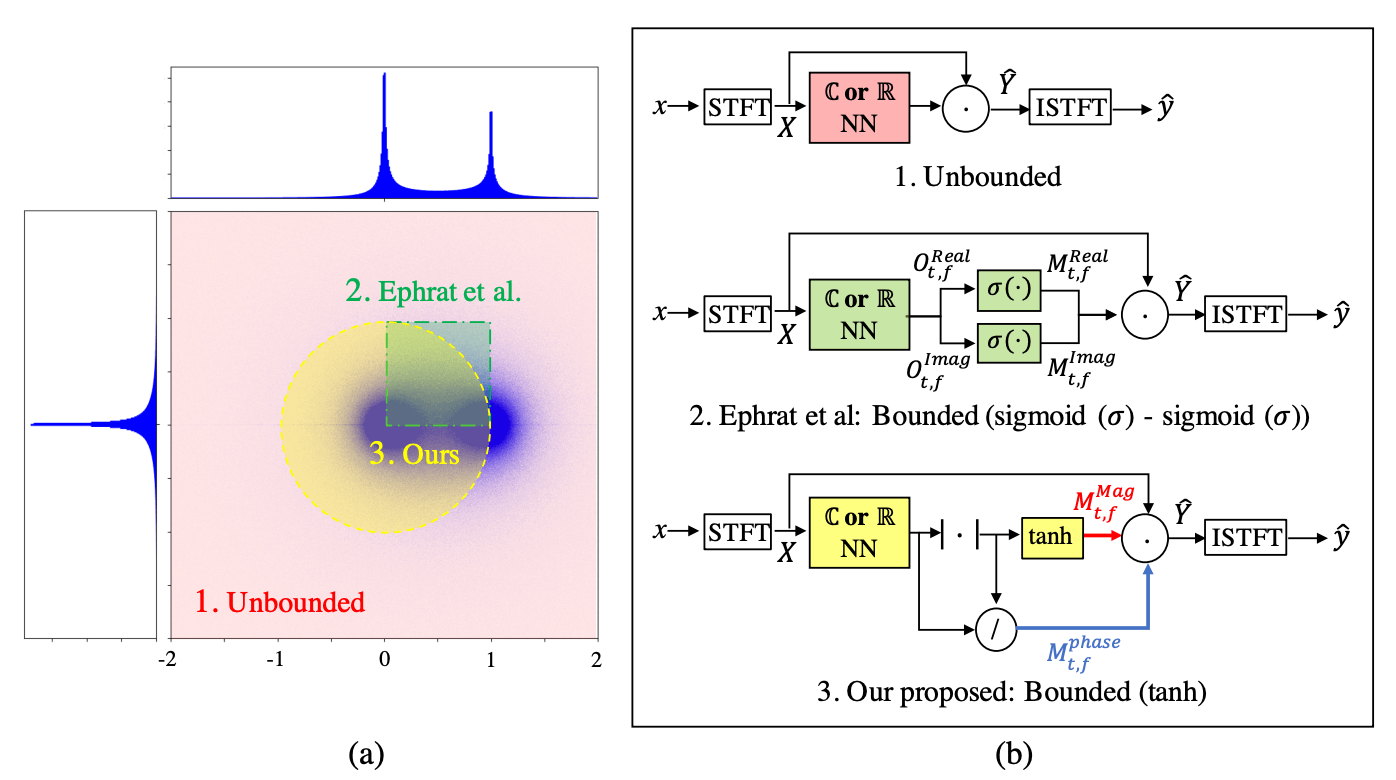
DCU-NetではcRMの推定を目指す。

  • RMは振幅のスケールを変えるだけで位相は変更しないので誤差が生じる
  • cRMは極座標上の回転もおこなうので、振幅に加え位相の誤差も修正できる。以下の式のようにマスクを使ってCleanを推定できるが、実部と虚部の値域が制限されていないため、パフォーマンスや学習が不安定になる。
\left.\hat{Y}_{t, f}=\hat{M}_{t, f} \cdot X_{t, f}=\left|\hat{M}_{t, f}\right| \cdot\left|X_{t, f}\right| \cdot e^{i\left(\theta_{\hat{M}_{t, f}}\right.}+\theta_{X_{t, f}}\right)

polar coordinate-wise cRM

  • tanhを用いてcRMの振幅を複素空間の単位円内[0, 1)に制限
  • 位相マスクについては、モデルの出力を振幅で割ると取得可能
\hat{M}_{t, f}=\left|\hat{M}_{t, f}\right| \cdot e^{i \theta_{\hat{M}_{t, f}}}=\hat{M}_{t, f}^{\text {mag }} \cdot \hat{M}_{t, f}^{\text {phase }}
\hat{M}_{t, f}^{\text {mag }}=\left\{\begin{array}{ll}\tanh \left(\left|O_{t, f}\right|\right) & \text { (bounded cond.) } \\\left|O_{t, f}\right| & \text { (unbounded cond.) }\end{array}, \quad \hat{M}_{t, f}^{\text {phase }}=O_{t, f} /\left|O_{t, f}\right|\right.

3.3 WEIGHTED-SDR LOSS

  • 損失関数で有名なのは平均二乗誤差（MSE）だが、これを複素TF領域で最適化すると位相の推定に失敗することが報告されている。
  • 代替案として、時間領域で定義された損失関数を使うことが可能。これは元の波形が位相情報を含んでいるから。

weighted-SDR

  • 元々のSDR損失関数は以下のように与えられる
\max _{\hat{y}} \operatorname{SDR}(y, \hat{y}):=\max _{\hat{y}} \frac{<y, \hat{y}>^2}{\|y\|^2\|\hat{y}\|^2-<y, \hat{y}>^2} \propto \min _{\hat{y}} \frac{\|\hat{y}\|^2}{<y, \hat{y}>^2}
  • 実際には以下のように負の逆数を最適化する
\operatorname{loss}_{V e n}(y, \hat{y}):=-\frac{<y, \hat{y}>^2}{\|\hat{y}\|^2}

  • しかし上のloss_{Ven}にはいくつかの重大な欠陥が存在する。

    1. −||\hat{y}||^2は\hat{y}の値に依存するため、トレーニング中に損失値に変動が生じる。

      ∵ 音声にちょって振幅の値が異なるので振幅が小さい場合は損失値が大きく、逆に振幅が大きい場合には損失が小さくなる。たぶん。

    2. y = 0の時、損失が０になるため、Noiseだけの音源から学習が不可能になる。

    3. 損失関数がスケールに対して敏感でなく、c ∈ R の場合、\hat{y} と c\hat{y} の損失値が同じになるという問題がある

      ∵ 式からわかるとおり、CleanとEst Cleanの比率を使っているから。

  • 以上の問題点を解決するために、分母の\|y\|^2を復活させて平方根を適用し、損失関数が\hat{y}に依存しないように変更。またこの変更で値域が[-1,1]に制限できる。

\operatorname{loss}_{S D R}(y, \hat{y}):=-\sqrt{-\frac{\operatorname{loss}_{V e n}}{\|y\|^2}}=-\frac{<y, \hat{y}>}{\|y\|\|\hat{y}\|}
  • CleanとNoiseの両方を予測し、それを用いてEst Noisyを作り出す。NoisyとEst Noisyの誤差を最小化するように学習する。\alpha=\|y\|^2 /\left(\|y\|^2+\|z\|^2\right)
\operatorname{loss}_{w S D R}(x, y, \hat{y}):=\alpha \operatorname{loss}_{S D R}(y, \hat{y})+(1-\alpha) \operatorname{loss}_{S D R}(z, \hat{z})

Discussion