Open69

E資格

osn_Lofiosn_Lofi

E資格については、勉強用に使える有効な学習書が1冊しかない。
いわゆる、インプレス社の黒本である。
この黒本は解説が非常に充実しているものの、一定の数学レベルがある人を対象に書かれていると思われ、難解なところが多い。
黒本の解説の解説として、このスクラップ記事を残す

osn_Lofiosn_Lofi

バッチ正規化とレイヤー正規化

バッチ正規化

出力xに対して、1バッチごとに正規化を行う。
バッチの中では平均、標準偏差は同じ。各層（チャンネル）ごとには異なる

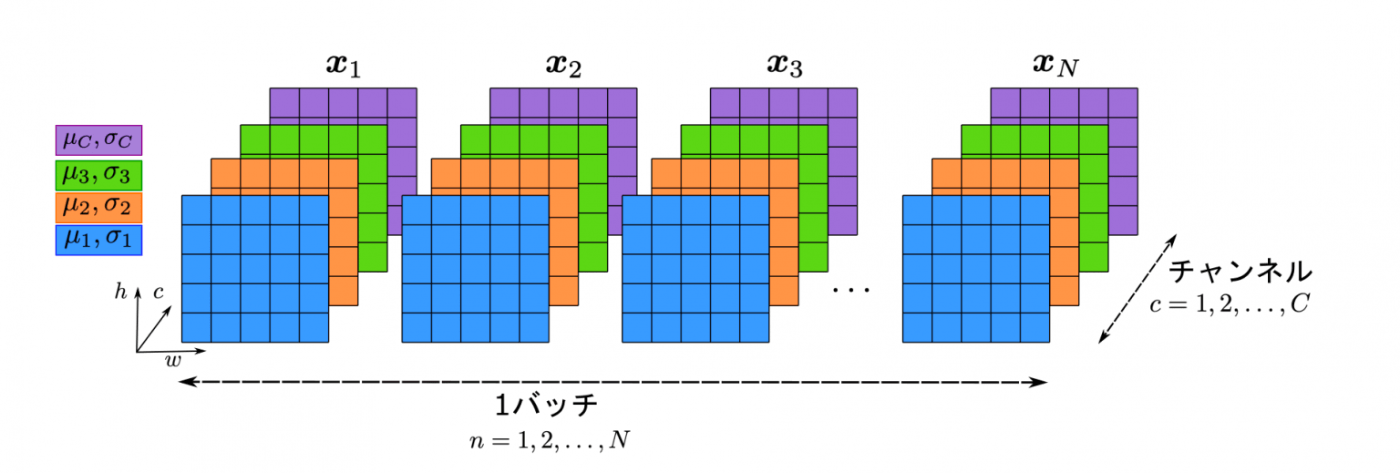
レイヤー正規化

層（チャンネル）単位で正規化を行う。
ミニバッチ内では平均、標準偏差が異なる。

osn_Lofiosn_Lofi

最適化アルゴリズム

SGD

\theta_{t+1} = \theta_t - \eta \frac{\partial L}{\partial \theta_t} 
for key in params.keys():
      params[key] -= self.lr * grads[key]

モーメンタム

v_{t+1} = αv_t - \eta \frac{\partial L}{\partial θ_t}
θ_{t+1}=θ_t + v_{t+1} 
for key in params.keys():
      self.v[key] = self.momentum * self.v[key] - self.lr*grads[key]
      params[key] += self.v[key]

ネステロフのモーメンタム

v_{t+1} = αv_t - \eta \frac{\partial L}{\partial Θ_t}
Θ_{t+1}=Θ_t +α^{2}v_t - (1+α)\eta \frac{\partial L}{\partial Θ_t} 
for key in params.keys():
 params[key] += self.momentum*self.momentum*self.v[key]
 params[key] -= (1 + self.momentum) * self.lr * grads[key]
 self.v[key] *= self.momentum
 self.v[key] -= self.lr * grads[key]
osn_Lofiosn_Lofi

畳み込みの手法別のパラメータ数

入力チャネル数C_{in}、出力チャネル数C_{out}、フィルタサイズfのとき \\

通常の畳み込み

パラメータ数　＝　C_{in} C_{out} f^2

デプスワイズ畳み込み

チャンネル方向の畳み込みは行わず、チャンネルごとに空間方向に畳み込みを行う

パラメータ数　= C_{in} f^2

ポイントワイズ畳み込み

フィルタサイズを1とした畳み込み

パラメータ数　＝　C_{in} C_{out}

入力特徴マップのサイズがD_F×D_Fでチャネル数をMとし、畳込みカーネルのサイズをD_K×D_K 、出力チャネル数をNとしてストライド 1 でパディングを適用した場合

通常の畳み込み

パラメータ数　= D_F * D_F * M * N * D_K * D_K

デプスワイズ畳み込み

パラメータ数　= D_F * D_F * M * D_K * D_K

ポイントワイズ畳み込み

パラメータ数　= M * N *D_F * D_F
osn_Lofiosn_Lofi
\frac{\partial L}{\partial W_{ij}} = \sum^m_{k= 1} \frac{\partial L}{\partial y_{k}}\frac{\partial y_k}{\partial w_{ij}}\\ = \frac{\partial L}{\partial y_1}\frac{\partial y_1}{\partial w_{1j}} + \frac{\partial L}{\partial y_2}\frac{\partial y_2}{\partial w_{2j}} + ・・・ + \frac{\partial L}{\partial y_i}\frac{\partial y_i}{\partial w_{ij}}\\ = \frac{\partial L}{\partial y_1}0+ \frac{\partial L}{\partial y_2}0 + ・・・ + \frac{\partial L}{\partial y_i}\frac{\partial y_i}{\partial w_{ij}}\\ =\frac{\partial L}{\partial y_i}x_i
osn_Lofiosn_Lofi

DQN

Atari2600のさまざまなゲームに対して、チューニングをせずに学習しても高い性能を示す。
特徴として、CNNによって行動価値関数を推定したことがあげられる。
ある時点のゲーム画面のキャプチャ画像を状態として受け取り、その時点である行動をとった場合の推定価値を取りうる行動ごとに出力する。

学習を安定させるための工夫

体験再生

各タイムステップにおけるエージェントの経験をデータ集合Dに蓄積する。学習時には、蓄積されたサンプルの中から、経験をランダムに取り出し、損失の計算を行う。

利点① 計算量の大きいエピソードの進行量を抑えることができる

パラメータの更新時に、同じ経験を何度も使えるため

利点② 更新の分散を軽減できる

経験をランダムに取り出すことで、系列方向の相関関係を断ち切ることができるため

利点③ パラメータの振動・発散を避けることができる

過去のさまざまな状態で行動分布が平均化されるため

目標Qネットワークの固定

価値関数が小さく更新されただけでも選ばれる行動が大きく変わってしまう問題に対して、目標値の算出に用いるパラメータを固定し、一定周期でこれを更新することで学習を安定させた。

損失関数

L(\theta）= \mathbb{E}_{s,a,r,s'〜D}[(r+ \gamma maxQ(s', a';\theta^-)-Q(s,a;\theta))^2]

報酬クリッピング

報酬の値を{-1, 0, 1}の3値に制限することで「報酬のスケールがタスクごとに大きく異なる」問題が解消され、学習率を調整する必要がなくなった。

osn_Lofiosn_Lofi

AlphaGoのパラメータ更新

第1ステージ：SL（教師あり学習）方策ネットワーク

盤面sのもとで人が選んだ手aに関する対数尤度を最大化する。
対数尤度を最大化するので勾配上昇法となる。

第2ステージ：RL（強化学習）方策ネットワーク

方策勾配法により学習する。

第3ステージ：価値ネットワーク

勾配降下法により学習する。

目標出力z（データ集合）を作るための対戦

時間ステップ 指し手の選び方
t = 1, .......U-1 SL方策ネットワーク
t = U ランダム
t = U+1, ......T RL方策ネットワーク
osn_Lofiosn_Lofi

方策勾配定理

\nabla_\theta J(\theta) =\sum_{s} d^{\pi\theta}(s) \sum_{a} \nabla_{\theta}\pi_{\theta}(a|s,\theta)Q^{\pi\theta}(s,a)
\nabla_\theta J(\theta) = \mathbb{E}_{\pi\theta}[\nabla_\theta \log\pi_{\theta}(a|s)Q^{\pi\theta}(s,a)]
osn_Lofiosn_Lofi

ベルヌーイ分布

確率変数　p^x (1-p)^{1-1}
期待値　p
分散　p(1-p)

尤度関数は確率変数の総乗

尤度関数　L_D(p) =\prod_{i=1}^{n} p^{x_i} (1-p)^{1-x_i}

負の対数尤度

尤度関数が最大になる最尤推定量を求める
計算を簡単にするために対数をとって足し算にする。
また、マイナスをつけることで最小値を求める問題に変える。

-\log L_D(p) = -\sum^n_{i =1} \log p^x_i (1-p)^{1-x_i} \\ =-\sum^n_{i=1} (x_i\log p +(1-x_i)\log(1-p))
osn_Lofiosn_Lofi

マルチヌーイ分布

f(x ; p) = \prod_{i=1}^{k} p_j^{x_j}

尤度関数

L_D(p) = \prod_{i=1}^{n} \prod_{j=1}^{k} p_j ^{x_{ij}}

負の対数尤度関数

-\log L_D(p) = - \sum^n_{i=1}\sum^k_{j=1} x_{ij} \log p_j
osn_Lofiosn_Lofi

等分散正規分布

最尤推定は二乗和誤差の最小化問題と同じになる（負の対数尤度を求めても、二乗和誤差の頭はマイナスにならないので注意）

確率密度関数

p(y_i) = \frac{1}{\sqrt{2\pi}\sigma} exp(-\frac{(y_i- f(x_i))^2}{2σ^2})

対数尤度関数

\log\prod_{i=1}^{n}p(y_i) = C - \frac{1}{2σ^2}\sum^n_{i=1}(y_i - f(x_i))^2
上式は結局、\sum^n_{i=1}(y_i - f(x_i))^2 の最小化問題ということになる
osn_Lofiosn_Lofi

情報量

ある事象が起きた時にそれがどれぐらい起こりにくいかを表す指標。
起こりにくい＝事象が起きる確率が低いほど、情報量が大きくなる。
情報量のことをエントロピーという

自己情報量　I(A) = \log \frac{1}{P(A)} =-\log P(A)
osn_Lofiosn_Lofi

平均情報量

情報量の平均値・期待値をいう。
一般的には平均情報量をエントロピーという場合が多い。

離散確率変数X=xとなる確率がp(x)の場合、確率変数Xのエントロピーは以下で表す。

H(X) = \sum_{x} p(x) \log \frac{1}{p(x)} = - \sum_{x} p(x)\log p(x)
osn_Lofiosn_Lofi

交差エントロピー

2つの確率分布がどれぐらい離れているかを表す指標
真の確率分布をp(x)、モデルの確率分布をq(x)とした場合に、以下で表される。
二つの確率分布が近いほど、交差エントロピーは小さくなる。

H(p, q ) = -\sum_{x} p(x) \log q(x)

例：
p = [1, 0, 0] q = [0.7, 0.2, 0.1]の交差エントロピーを求める

H(p, q ) = - 1 * \log 0.7 + 0 + 0 = 0.35

ベルヌーイ分布のときの交差エントロピー

負の対数尤度と同じ

H(p, q ) = - p(x) \log q(x) - (1-p(x))\log (1-q(x))
osn_Lofiosn_Lofi

カルバックライブラー・ダイバージェンス

2つの確率分布の近さを表現する基本的な量。
交差エントロピーよりも、より直感的にその近さを表してくれる。

D(p||q) = \sum_{x} p(x) \log \frac{p(x)}{q(x)}

実はKLダイバージェンスは、交差エントロピーから求められる。
pのエントロピーをH(p)、pとqの交差エントロピーをH(p,q）とすると

H(p, q) = H(p) + D(p||q) \\
H(p,q)= -\sum_{x} p(x)\log p(x) +\sum_{x} p(x) \log \frac{p(x)}{q(x)} \\
H(p, q ) = -\sum_{x} p(x) \log q(x)

KLダイバージェンスの別の表記

q(x)を分子に持ってくると、KLダイバージェンスの符号はマイナスになるので注意！

D(p||q) = - \sum_{x} p(x) \log \frac{q(x)}{p(x)}
osn_Lofiosn_Lofi

ResNet

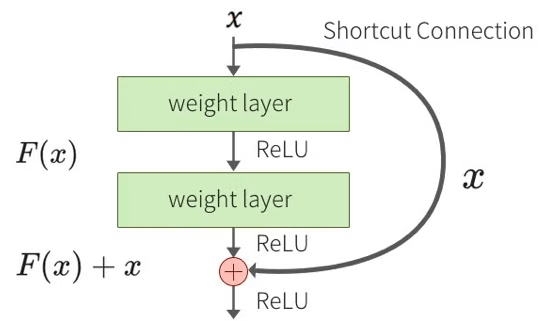
ResNetでは層をまたがる結合として、identify mappingを用いる。
ResNetがうまくいくのは、ブロックの入力にこれ以上の変換が必要ない場合は重みが0となり、小さな変動をより見つけやすくなること、勾配消失が起きにくいこと、アンサンブル効果があることにある。

osn_Lofiosn_Lofi

GoogleNet

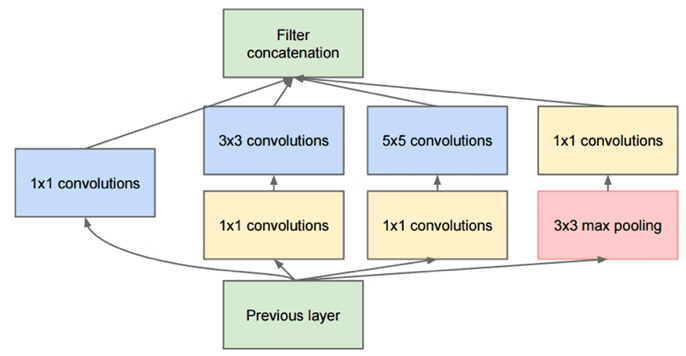
inceptionモジュール

1×1の畳み込みを積極的に使う→次元削減と同等の効果。
小さな畳み込みフィルタのグループで近似する→モデル表現力とパラメータ数のトレードオフを改善。
異なるサイズの畳み込みを独立して行なっているため、非ゼロのパラメータ数が大きく減る。

auxililary loss

サブネットワークでのクラス分類を行う。
勾配消失を防ぐ、ネットワークの正規化を実現。
バッチ正規化を加えることで、学習がうまく進むことがある。
アンサンブル学習と同様の効果が期待できる。

osn_Lofiosn_Lofi

R-CNN

CNNで抽出した特徴量を使って、SVMで領域を分類する。単純な2クラス分類。つまり、物体か背景か。
回帰によって、物体領域を推定する（バウンディングボックス）

SelectiveSearchで抽出した大量の物体領域候補を、resizeしてCNNで特徴抽出し、SVMで分類するため計算コストが高い。

osn_Lofiosn_Lofi

Mask R-CNN

Faster R-CNNの拡張版で、物体検出であるバウンディングボックスとカテゴリに加え、物体のセグメンテーションマスクを出力。

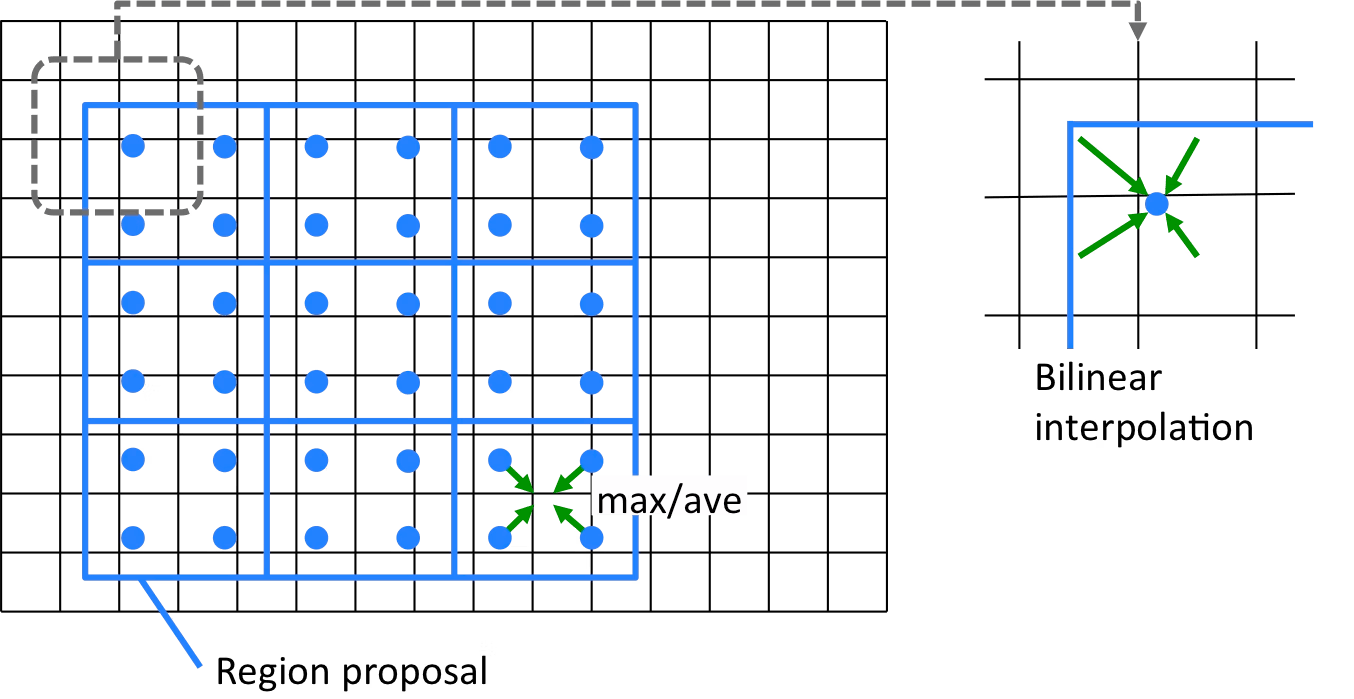
Rol Align

領域候補の抽出に、Rol PoolingからRolAlignを採用。
Rol Poolingでは座標を整数値で丸めることでバウンディングボックスを得ており、物体検出にようにあるていどの誤差が許されるのであれば問題なかった。
セグメンテーションの場合はピクセルの位置づれが致命的になるため改善された。
丸め込みではなく、近傍4ピクセルからの補完で算出。

osn_Lofiosn_Lofi

SegNet

Max Pooling インデックスを使用することでFCNよりメモリ効率が良い

osn_Lofiosn_Lofi

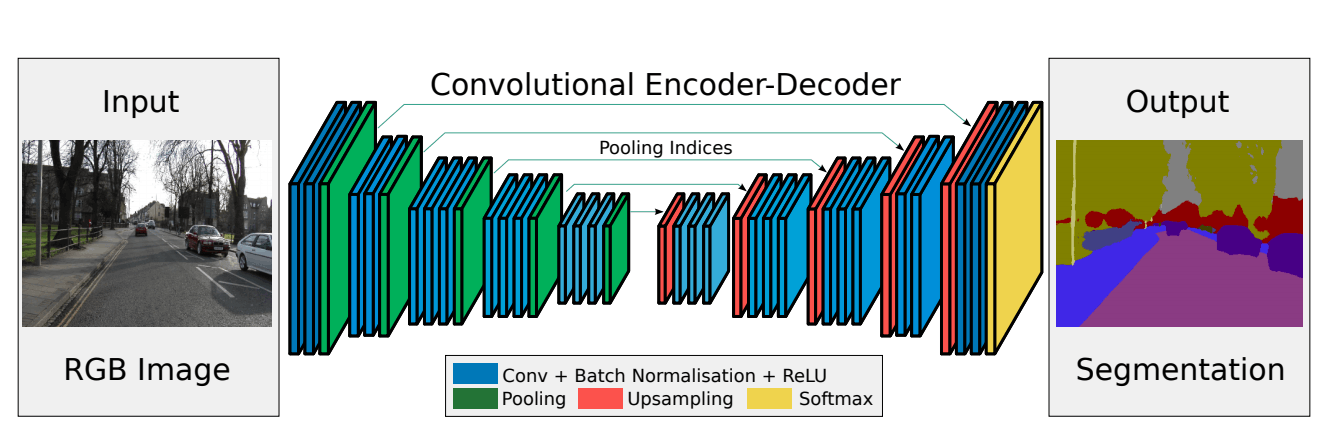
Resnet

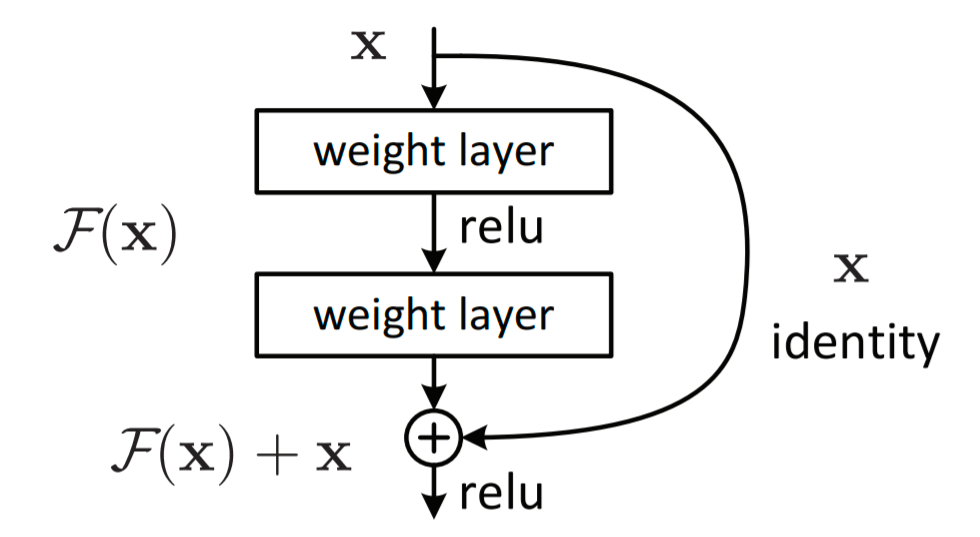
残差学習

ResNetでは下図のような残差ブロックを繰り返して構成する。
残差＝residueからResNetという名前が来た。
残差ブロックを導入することで、層を深くすることができ、精度向上を果たすことができた。

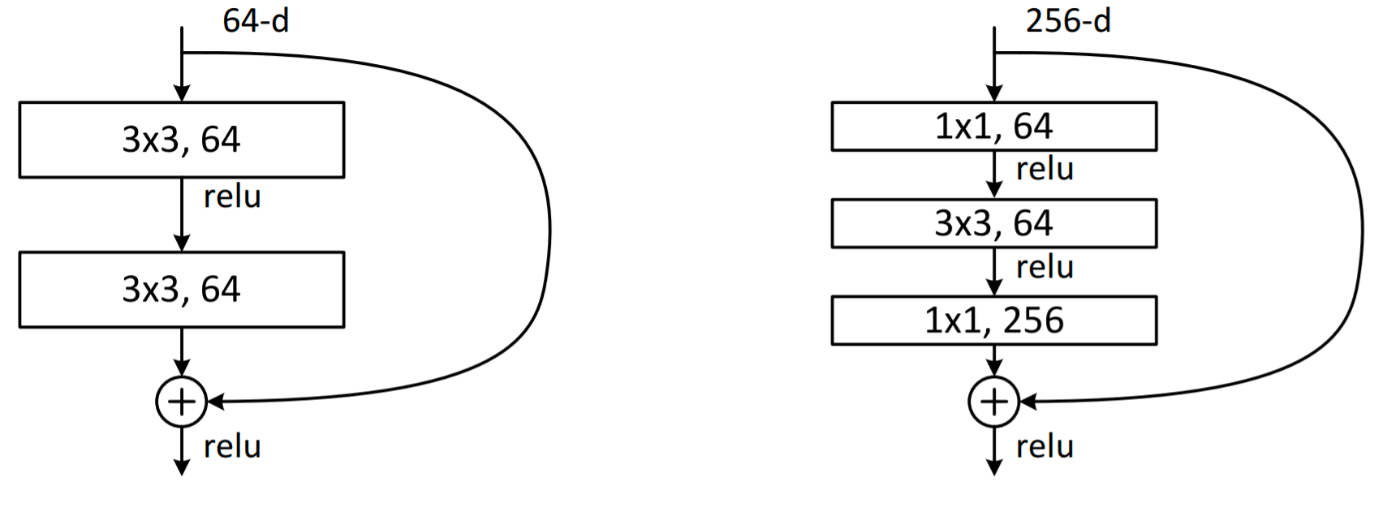
Bottleneckブロック（ボトルネックブロック）

右図がbottleneckブロックと呼ばれる。プレーンな層より1層多くなる。1×1と3×3のConvolutionで出力のDepthの次元を小さくしてから、最後の1×1でDepthの次元を復元することから、Bottleneckという名前がついている

Heの初期化

活性化関数にReLUを用いる場合の最適な重みの初期化が提案。
重みの初期値は平均0、標準偏差√（2÷n)の正規分布から生成する。

osn_Lofiosn_Lofi

WideResNet

残差学習における性能改善　残差ブロックの幅を広げる

ResNetの深さ（Depth）を減らし、代わりにブロック内のチャネルの幅（Width）を増やすことで性能に対する計算効率を向上させた

ドロップアウト

ブロック内にドロップアウトを加えることで性能を向上させた

osn_Lofiosn_Lofi

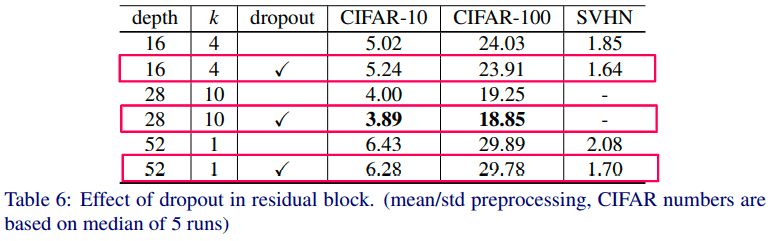
EfficientNet

ネットワークの深さ・幅・解像度をバランスよく

ネットワークの深さ・幅・解像度を最適化しながらスケールアップするkとおで、小さなモデルで効率よく高い精度を達成した。
ポイントは「小さなモデル」。従来のモデルよりパラメータ数を減らすことに成功した。

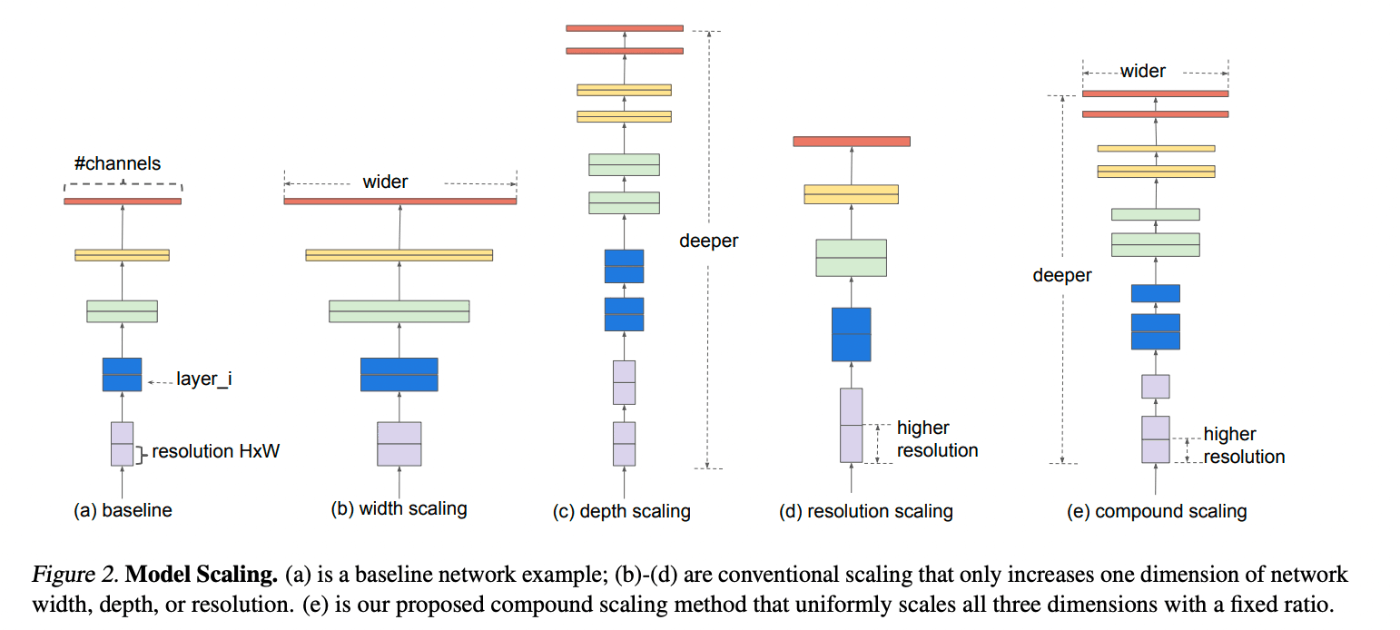
Compound Coefficient

幅・深さ・解像度などを何倍に増やすかを、複合係数（Compound Coeficient)と呼ばれる係数を導入することで最適化した。

osn_Lofiosn_Lofi

FCOS Fully Convolution One-Stage Object Deteciton

物体検出モデル。
Faster R-CNNなどの従来の物体検出モデルでは、アンカーボックス（バウンディングボックスを出力するための無数の候補）を事前に定義する必要があった。FCOSはアンカーフリーで、アンカーボックスを使用しない物体検出モデルになる。

アンカーボックスの課題

  • ハイパーパラメータの設定が面倒
  • ポジティブサンプルとネガティブサンプルの数が不均衡

Center-ness ブランチ

FCOSの特徴の一つにCenter-nessブランチが導入されたことがある。

osn_Lofiosn_Lofi

VQ-VAE (Vector Quantised-Variational AutoEncorder)

VAEでは潜在変数を連続変数として扱っていたが、この潜在変数を離散変数として扱う。
自然界の様々な物事の特徴を捉えるには離散変数の方が適しているとの考え方からきている。（猫が犬に連続的に変化することはない）

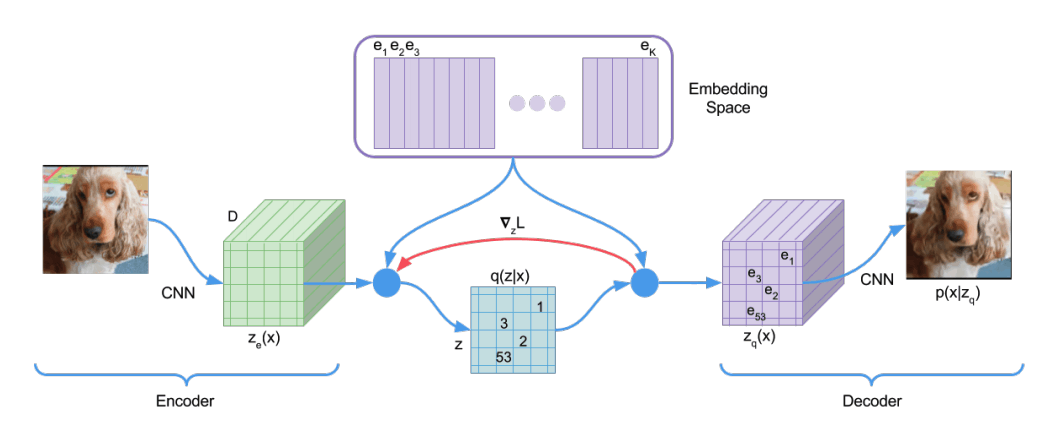
VAEで起こりうるposterior collapseの問題を回避し、VAEより鮮明な画像を生成。

osn_Lofiosn_Lofi

GAN

教師なしでデータから特徴を学習して、画像を生成するモデル
生成器は乱数を入力すると元のデータに偽のデータを生成する
識別器は偽のデータと本物のデータのどちらかを識別する

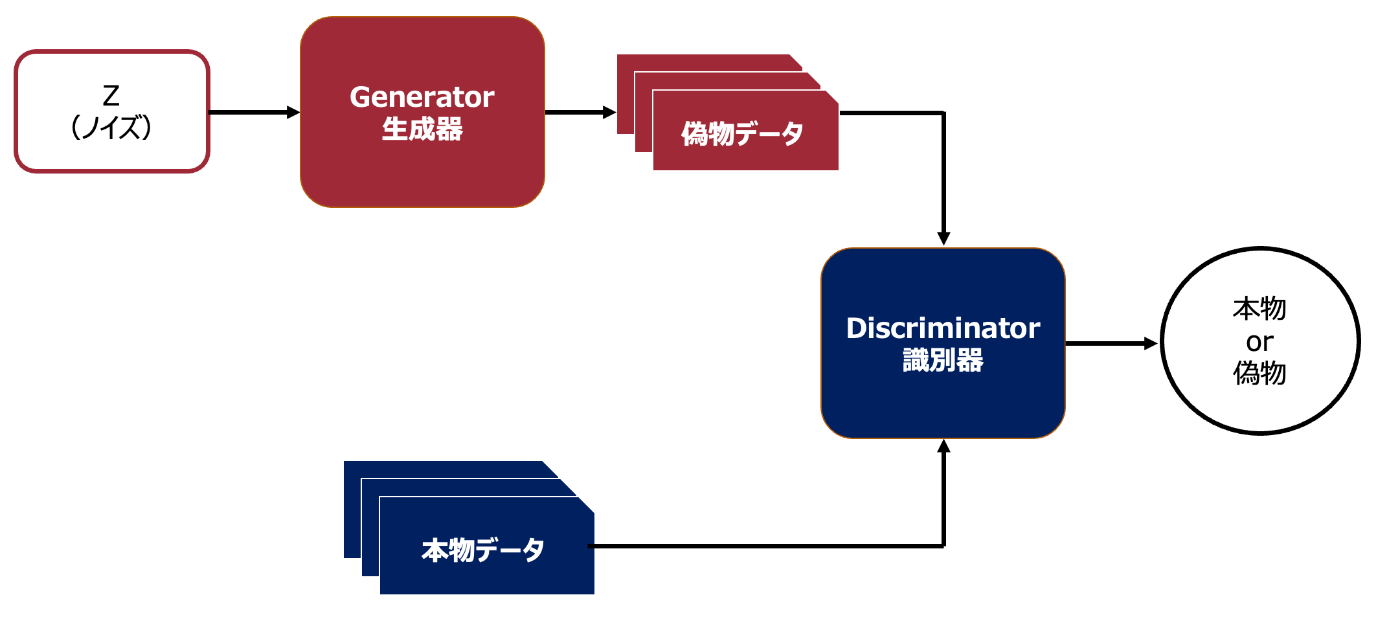
Generator（生成器）はランダムノイズから画像を生成する
Discriminator（識別器）は入力された画像が本物か偽物かどうかを予測する

両者を交互に学習することで
・生成器が識別器を騙せる偽物画像を作るのが上手くなる
・上手く生成された偽物画像を識別器が見破るのが上手くなる
・生成器は識別能力があがった識別器を騙すためにさらに偽物画像を作るのがうまくなる

GANの最適化問題は、

識別器（D)を最大化し、生成器（G)を最小化する
識別器（D)は本物のデータxと、生成器から出力された偽のデータG(x)に対して、真のデータxである確率を出力する。それぞれの確率をD(x)、D(G(x))とすると、識別器は、D(x)と1ーD(G(x))の確率の期待値の和を最大化するよう学習する。

一方、生成器は、生成されたデータが本物である確率D(G(x))を最大化しようとするので、1-D(G(x))の大数の期待値を最小化する。

学習

生成器（G)：

識別器（D)の重みを固定して、偽物のラベルを1（本物）として学習。
→本物と近い画像を生成する。（識別器を通して学習。識別器のパラメータは固定されているので、生成器のパラメータが更新される）

識別器（D)：

通常の画像分類として学習

osn_Lofiosn_Lofi

DCGAN (Deep Convolution GAN)

生成器と識別器に全結合層ではなく、畳み込み層を使用することで、より自然な画像を生成できるようにした。

生成器（G)

・生成器では転置畳み込みを使用してアップサンプリングを行う。
・生成器の活性化関数にはReLUを用いて、出力層のみTanhを用いる。

識別器（D)

・識別器ではプーリングではなくストライドでダウンサンプリングを行う。
・識別器のすべての層の活性化関数にLeakyReluを用いる。

共通

・生成器と識別器にBatchNormalizationを使用する。
・隠れ層の全結合層を除く。

osn_Lofiosn_Lofi

Transformer

Attention is you need

memoryをkey とvalueに分ける。
queryとkeyからattention_weightを算出し、valueを組み合わせて最終的な出力としている。

query 入力の単語から検索をかける
key　queryとmemoryの類似度
value 最終的な出力

Attention

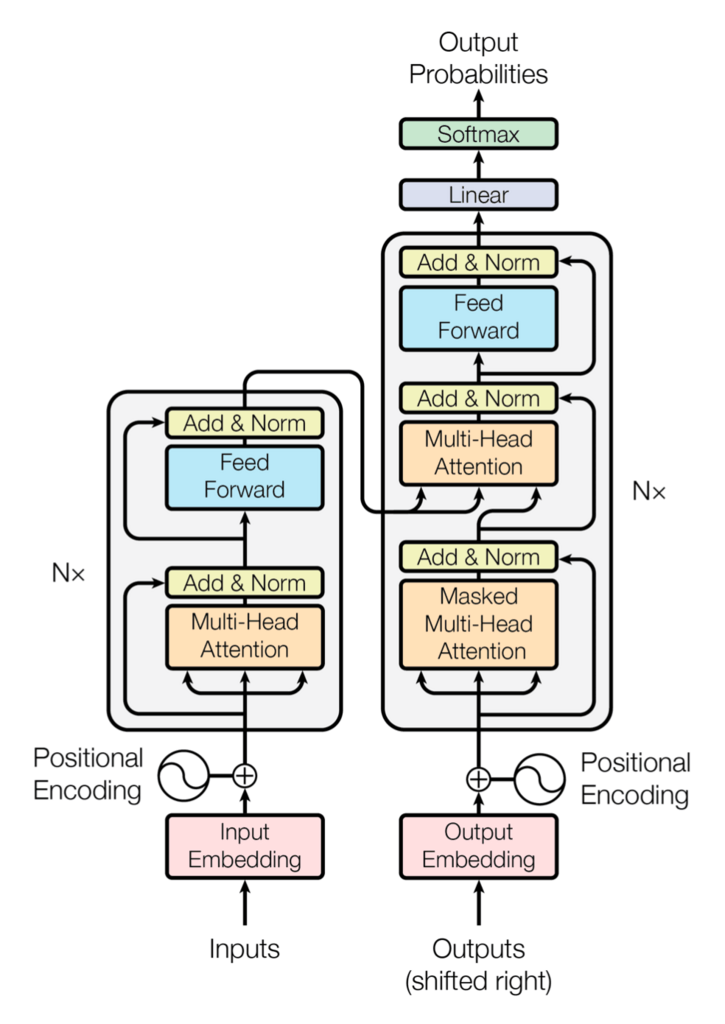
Attention(Q, K, V ) = softmax(\frac{Q K^T}{\sqrt{d_k}})V
\sqrt{d_k}はqueryとkeyの次元で求められる値。\\ d_kが大きくなると逆伝播時のソフトマックスの勾配が小さくなるので、\sqrt{d_k}で除す

Encorderのマルチヘッドアテンション

EncorderのマルチヘッドアテンションはSelf-Attentionが使用されている。
Self-Attention とは、inputとmemoryが全く同じデータを用いている場合に使用する。

Decorderのマルチヘッドアテンション

DecorderのマルチヘッドアテンションはSelf-AttentionとSource Target Attentionの二つある。

１つ目のマルチヘッドアテンションはSelf-Attenttion。Mask処理がなされる。
Mask処理がなされた単語は、ソフトマックス関数にかけられる前に**-∞**に置き換えられる

2つ目のマルチヘッドアテンションは Source Target Attention。
Source Target Attentionはinputとmemoryが違うデータを用いる場合に使用する
Encorderからkeyとvalueを受け取り、Decorderの２つ目のマルチヘッドアテンンションまでの出力をqueryとしてAttentionを計算する

osn_Lofiosn_Lofi

フーリエ変換

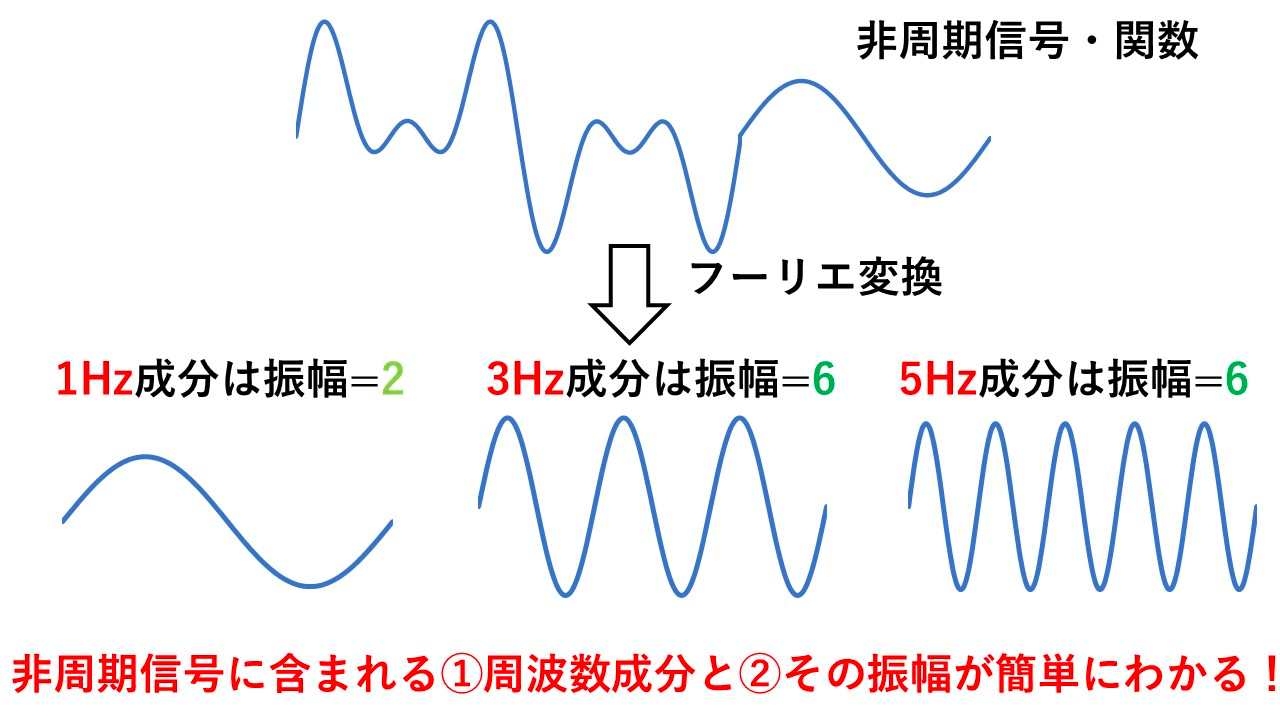
ざっくり考えると、非周期的な波形に、どのような周波数成分（Hz)が、どの程度の大きさ（振幅）で含まれるかを知ることができる手法。
時系列データを周波数データに変換する。

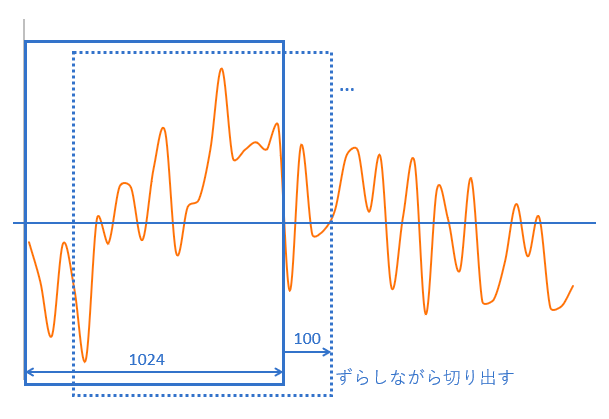
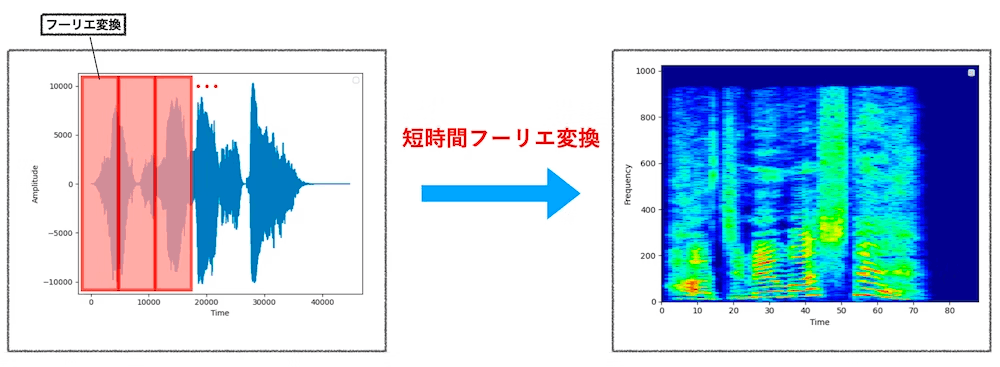
短時間フーリエ変換

フーリエ変換の応用。フーリエ変換は音声波形の周波数成分を出す処理だが、時間成分も知るために、音声波形の範囲（時間）を、重複部分のある短いスライスに分け、フーリエ変換を行う。

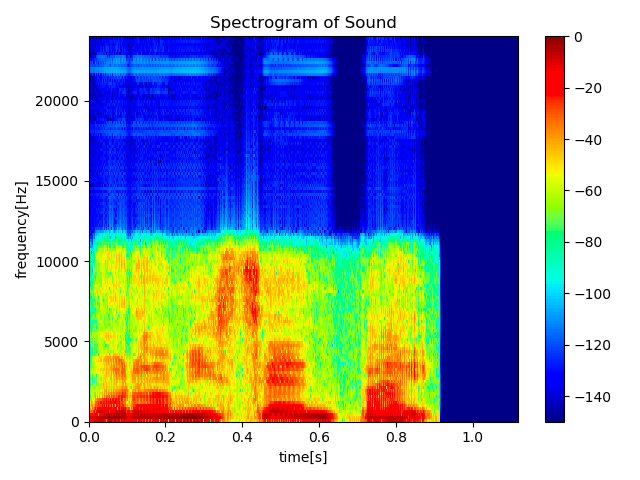
スペクトログラム

信号を時間周波数分析をすることで得た情報を図として描画したもの

osn_Lofiosn_Lofi

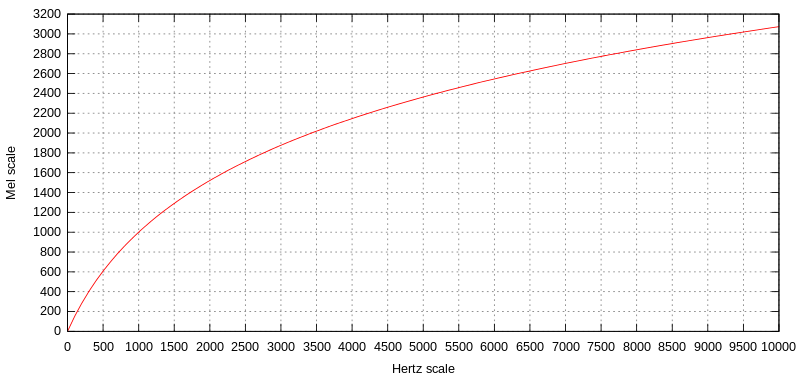
メル尺度

信号の周波数を対数変換したもの。人間は低周波数の音の違いを判別することはできるが、高周波数の違いを判別することはできない。
メル尺度の差が同じであれば、人間が感じる音高の差が同じになることを意味している。
メルという名称はメロディに由来する。

m = 1127* \log(\frac{f}{700} +1)

osn_Lofiosn_Lofi

音声サンプリング

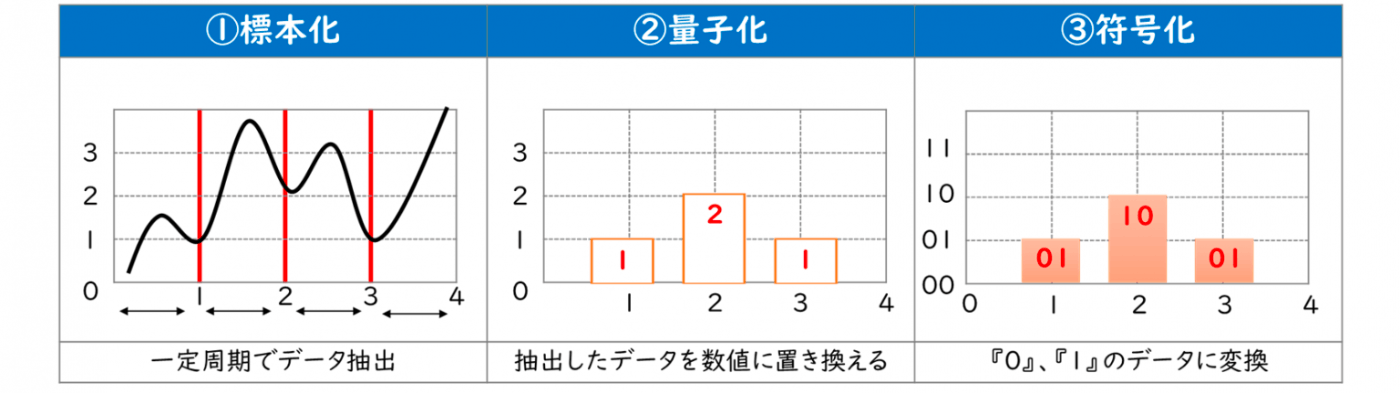
標本化（サンプリング）

アナログ信号から、一定の時間間隔で区切ってデータを採取すること。
この時間間隔を「標本化周波数（サンプリング周波数）」と呼び、Hzという単位で表す。
1秒間に1回が1Hz。
CDのサンプリング周波数は44.1kHzであり、1秒間に44.1×1,000回のデータ採取を行う。

量子化

標本化で採取したデータを数値にすること。
この数値の大きさを量子化ビット数と呼ぶ。
CDの量子化ビット数は16ビット。

符号化

量子化で得られた数値を特定の形式にすること。
数値を0、1からなるデジタルデータに変換する。

osn_Lofiosn_Lofi

A3C (Asynchronous Advantage Actor-Critic)

概要

従来の強化学習では強力なGPUと膨大な学習時間が必要だった。A3Cでは、マルチコアCPUのみを用いて、かつこれまでの手法の半分程度の時間で、高精度の成果をあげた。
そのアルゴリズムが、3つのAから始まることからA3Cと呼ばれている。
Asynchronous（非同期）
Advantage（アドバンテージ関数）
Actor-Critic(Actor-Critic法）

Actor-Critic法

強化学習のエージェントが行う方策改善と方策評価の二つの機能を分離し、個々に学習してモデル化した。
方策改善を行う部分を行動器（Actor )といい、方策評価を行う部分を評価（Critic)という。

方策勾配定理

通常の方策勾配定理

\nabla_\theta J(\theta) = \mathbb{E}_{\pi\theta}[\nabla_\theta \log\pi_{\theta}(a|s)Q^{\pi\theta}(s,a)]

Actor-Critic法の方策勾配定理

\nabla_\theta \rho_{\theta} = \mathbb{E}_{\pi\theta}[\nabla_\theta \log\pi_{\theta}(a|s)(Q^{\pi\theta}(s,a)-b(s))]

アドバンテージ関数で複数ステップを先読みして勾配を求めるのが特徴。

Q^{\pi\theta}(s,a)-b(s)をアドバンテージ関数という。
osn_Lofiosn_Lofi

距離学習(Metric Learning)

概要

異常検知や分類問題、顔認識、画像認識などで注目されている。
似たデータ同士は近づき、似ていないデータ同士は離れるようにデータを埋め込み空間にマッピングする

深層距離学習

  • 同じクラスに属する（類似）サンプルから得られる特徴量ベクトル間の距離を小さく
  • 異なるクラスに属する（非類似）サンプルから得られる特徴量ベクトル間の距離を大きく
    となるように深層ニューラルネットワークを学習する。
    距離はユークリッド距離やコサイン類似度が用いられる。

Contrastive Loss

2サンプルを1組みして距離を学習

Triplet Loss

3サンプルを1組みにして距離を学習

osn_Lofiosn_Lofi

メタ学習

学習の仕方を学習する。
英語を学習すると、言語の学習の仕方を学ぶことができる。そこで学んだ学習の仕方を応用することでスペイン語を効率よく学べたりする。こうした学習の仕方を学習していくことがメタ学習。

MAML（Model-Agnostic Meta-Learning)

良い初期値を学習する
メタ学習の汎用性を大きく改善した手法。
微分可能であればどのようなモデル・損失関数でも適用可能。

メタ学習の評価方法 Few-Shot-Learning

非常に少ないデータのみを用いて学習し、新たなタスクを解く。
データ数が1つだけの場合をone-shot learning。データ数がゼロの場合をzero-shot learningという。

osn_Lofiosn_Lofi

グラフニューラルネットワーク

ここで言うグラフとは、各ノードとノード間のつながりを表すエッジで表現される。
世の中にはこのようなグラフで表現できることが数多く存在する。例えば、SNSでのつながりやタンパク質の構造など。
グラフで表されるデータを分類したり、グラフ構造を推定すること。

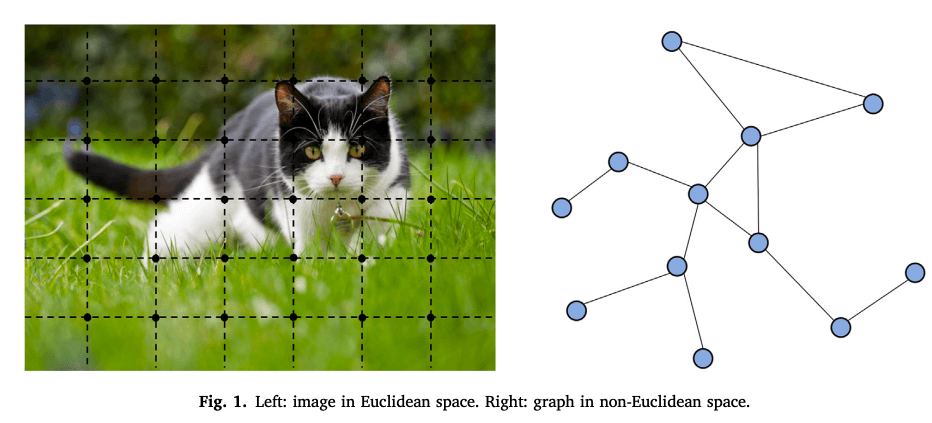
Spectalアプローチ

グラフ構造にグラフフーリエ変換を施すことで畳み込み演算を行う。
畳み込み演算後、逆グラフフーリエ変換を行うことで再びグラフのカタチに戻す。

Spatialアプローチ

グラフ変換せずにそのまま畳み込み演算する。

osn_Lofiosn_Lofi

CTC (Connectionist Temporal Classification)

音声認識におけるラベル付けの問題を解消する方法として考案された学習方法。
音声認識では、「音声の何ミリ秒から何ミリびょうまでが”a”という文字に対応している」といったアノテーションが必要だが、音声の場合、アノテーションコストが高いだけでなく、曖昧性や非決定性がある。
こういった課題に対し、ラベル系列（文字系列）を直接学習する方法としてCTCがあみだされた。

CTCの損失関数

L_{CTC} = -\log (p(x))

ネットワークの学習

CTCでは動的計画法の一つである前向き・後ろ向きアルゴリズムを使用して計算が行われる。

osn_Lofiosn_Lofi

説明可能なAI

説明技術に関する整理

大局説明と局所説明
モデル依存と非モデル依存
非モデル依存とは、説明技術がさまざまなモデルに対して適用できるもの

LIME

局所説明かつ非モデル依存。
説明したいサンプルに近いデータを生成して、そのデータのみ説明性の高い線形性モデルで再度フィッティングすることで、線形モデルを使った解釈を対象のサンプルに適用する考え方。

SHAP

非モデル依存。大局説明・局所説明のいずれも可。
ゲーム理論において、プレイヤーの寄与を算出するシャープレイ値をベースにした手法

osn_Lofiosn_Lofi

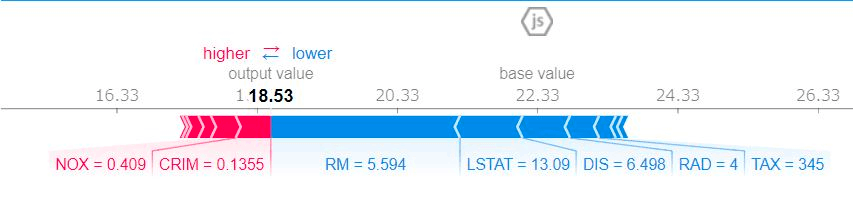
Grad-CAM (Gradient-weight Class Activation Mapping)

予測値に対する勾配を重みづけすることで、重要なピクセルを可視化する技術
勾配が大きいピクセルは予測値に大きな影響を与えるという考え方に着想している。

結果の可視化が可能になることで

  1. モデルへのデバック
  2. 根拠の説明
  3. 人間への新たな示唆の提供
    の3側面で良い効果がもたらされる。
osn_Lofiosn_Lofi

分散処理

計算リソースをうまく活用して、効率的な計算を行う

データ並列とモデル並列

データ並列

親モデルをコピーしたn個のレプリカ（子モデル）を各GPUワーカーに配置し、異なるバッチを各GPUワーカーに供給する。

モデル並列

モデルの各部分を別GPU上にロードする

その他ポイント

モデル並列は、モデルが複雑になると使いづらくなるため、一般的にはデータ並列が使われる。
同期型のデータ並列処理は、非同期型のものに比べて収束性が良い傾向にある

osn_Lofiosn_Lofi

サポートベクトルマシン

教師あり学習モデルで、主にマージン最大化を基準として学習される。
マージンを決定する点と、マージンの内側の点をサポートベクトルという。
サポートベクトル以外の点が、境界面の決定に影響しないことから、サポートベクトルマシンは外れ値に対してロバスト（影響を受けにくい）なモデルといえる。
学習時間がかかるため、大量のデータを利用した学習には向かない。
サポートベクトルマシンの出力は確率として解釈できないため、ロジスティック回帰のように事後的に境界面を調整することはできない。

osn_Lofiosn_Lofi

L1正則化

パラメータの絶対値の総和（L1ノルム）をペナルティとする。
L1正則化には、パラメータの数を減らす効果がある。

L1正則化：J(\theta)+\lambda\sum_i|\theta_i|
osn_Lofiosn_Lofi

Adam

指数移動平均を用いて過去の勾配情報を累積し、モーメンタムと学習率適応の両方を実現する。

m_{t+1} ← \rho_1 m_t + (1 -\rho_1) \frac{\partial L}{\partial \theta_t}
v_{t+1} ← \rho_2 m_t + (1 -\rho_2) \frac{\partial L}{\partial \theta_t} \bigodot \frac{\partial L}{\partial \theta_t}
\hat {m_{t+1}} ← \frac {m_{t+1}} {1- \rho_1^t}
\hat {v_{t+1}} ← \frac {v_{t+1}} {1- \rho_2^t}
\theta_{t+1} = \theta_t - \eta \frac {1} {\sqrt{\hat v_{t+1}} + \epsilon} \bigodot \hat m_{t+1} 
for key in params.keys():
   self.m[key] = self.rho1 * self.m[key]+ (1-self.rho1)*grad[key]
   self.v[key] = self.rho2 * self.v[key]+ (1-self.rho2)*(grad[key] **2)
  
   m = self.m[key]  /  (1- self.rho1**self.iter)
   v = self.m[key]  /  (1- self.rho2**self.iter)

   params[key] -= self.lr * m / (np.sqrt(v) +self.epsilon)
osn_Lofiosn_Lofi

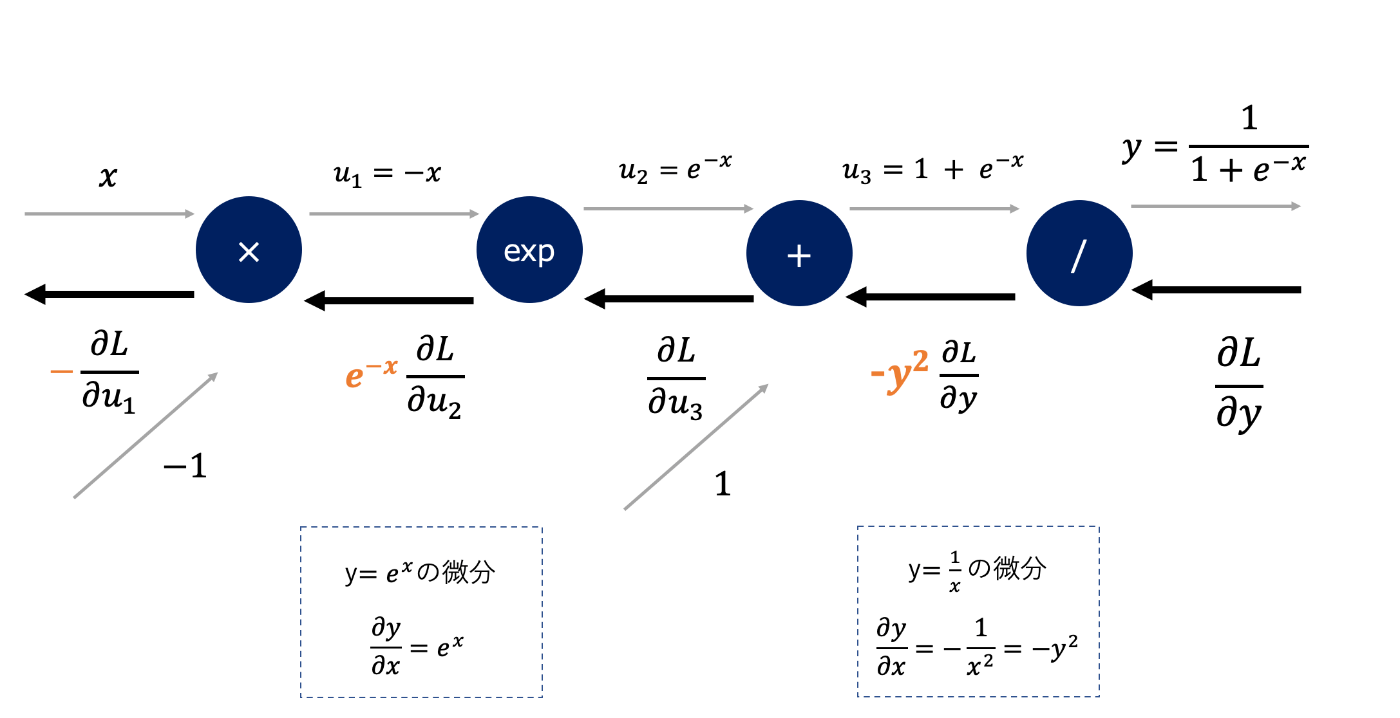
Sarsa (TD学習）

行動価値関数を更新する際、Q学習に比べて行動価値の小さい探索結果が反映されやすい

Q(S_t, A_t)←Q(S_t, A_t)＋α[R_{t+1} +\gamma Q(S_{t+1}, A_{t+1}) - Q(S_t,A_t)]
  • 方策オン型の手法であり、行動を決定する方策と行動価値関数の更新に利用される方策が同じ。
osn_Lofiosn_Lofi

Q学習

行動価値関数を更新する際、Sarsaに比べて行動価値の小さい探索結果が反映されにくい

Q(S_t, A_t)←Q(S_t, A_t)＋α[R_{t+1} +\gamma maxQ(S_{t+1}, a') - Q(S_t,A_t)]
  • Sarsaより行動価値関数の収束が早くなることが多いが、必ずしもそうなるとは限らない。
  • 行動を決定する方策と行動価値関数の更新に利用される方策は異なる。
  • 行動価値関数Qの更新が行動の決定方法に依存しない。
osn_Lofiosn_Lofi

状態価値関数と行動価値関数の関係

状態価値関数Vは、方策πと行動価値関数Qの積で表される

V^{\pi}(s) = \sum_a \pi(a | s) Q^{\pi}(s,a)

ベルマン方程式

状態価値関数

V^{\pi}(s) = \sum_a \pi(a | s) \sum_{s', r} P(S', r| s,a)[r + \gamma V^{\pi}(s')]

行動価値関数

Q^{\pi}(s, a) = \sum_{s', r} P(S', r| s,a)[r + \gamma V^{\pi}(s')]
osn_Lofiosn_Lofi

バッチ学習・ミニバッチ学習・オンライン学習

バッチ学習：すべてのデータを投入してモデルを学習
ミニバッチ学習：データを小さなグループ（ミニバッチ）に分割してモデルを学習
オンライン学習：データを一つずつ与えてモデルを学習

osn_Lofiosn_Lofi

numpyでDropoutを実装

import numpy as np

class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def foward(self, x, train_flag=True):
        #訓練時
        if train_flag:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x*self.mask
       #予測時 
　　else:
　　　#予測時は1ードロップアウト比率で計算する＝残る確率。
            return x*(1-self.dropout_ratio)
    
    def backward(self, dout):
        return dout * self.mask

3×3の行列xを作る

[in]
x = np.random.rand(3,3)
x

[out]
array([[0.26329059, 0.12489402, 0.05607279],
       [0.85869877, 0.76627507, 0.40834017],
       [0.9754227 , 0.69723063, 0.06930745]])

xと同じshapeで、各要素が0〜1になるような行列をつくり、各要素が0.5（dropout_ratio)を上回っている場合は1(True)を、そうでない場合は0(False)を返し、変数maskに格納する

[in]
mask = np.random.rand(*x.shape) > 0.5
mask

[out]
array([[ True,  True, False],
       [False,  True, False],
       [ True,  True, False]])

xにmaskを乗じる。
dropout_ratioを上回る要素だけが残る。

[in]
x*mask

[out]
array([[0.26329059, 0.12489402, 0.        ],
       [0.        , 0.76627507, 0.        ],
       [0.9754227 , 0.69723063, 0.        ]])
osn_Lofiosn_Lofi

正則化

https://di-acc2.com/analytics/ai/6335/

学習データへの過剰フィッティングをおさえ、より単純で低次元のモデルとして表現することを目的とする。

実際と予測との誤差　＝　バイアス　＋　バリアンス　＋　ノイズ
ノイズはどうしようもない。→バイアスとバリアンスを下げるよう、モデルをチューニングしていく。
バイアスが高いとは モデルが学習データの特性を捉えきれていないということ＝過小適合。特徴量を増やしたり、決定木であれば深さを深くしたりして、モデルを複雑にすれば過小適合は解決できる。

バリアンスが高いとは モデルを複雑にした結果、学習データに対してオーバーフィッティングし、モデルの汎化性能が下がっている状態＝過剰適合。過学習を抑える手段の一つが正則化。

正則化の概念

パラメータ（重み）にペナルティを科すための追加情報バイアス）を導入する。
損失関数を最小化させるパラメータW0とW1を考えた時、単純に損失関数の最小値を探しに行くと過学習する可能性がある。→W0とW1のパラメータが大きくなる。
ペナルティ項を導入することで、W0とW1のパラメータが大きくなりすぎないようにする。

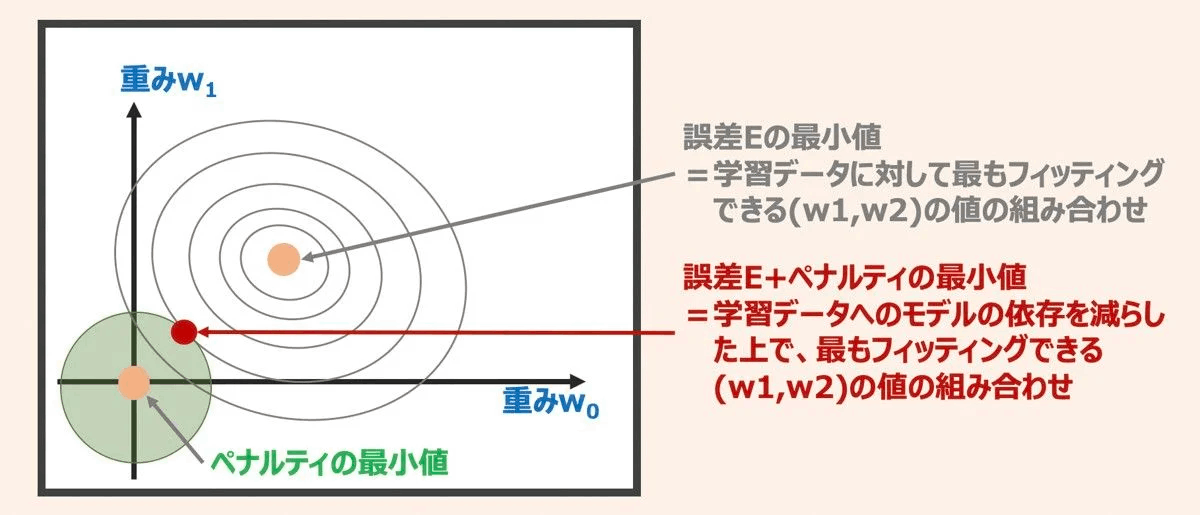
L2正則化

重みの2乗をペナルティに取り入れる。
一般的に重み減衰とも言われる。
重みが原点から離れるほどペナルティが大きくなる。

L1正則化

重みの絶対値をペナルティに取り入れる。
重み係数の取りうる範囲は菱形の角の部分になる。
あまり重要でない説明変数のパラメータ（重み）をゼロにする効果がある。

osn_Lofiosn_Lofi

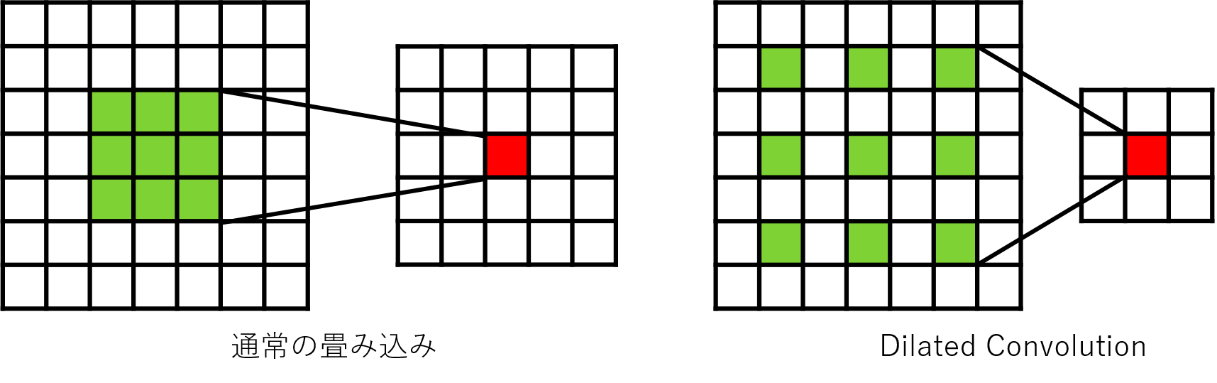
ダイレイト畳み込み

フィルタの適用範囲を広げながら畳み込む。
通常の畳み込みより受容野が広くなる。
セマンティックセグメンテーションや音声認識で使われる。

osn_Lofiosn_Lofi

Goodfellow のCNNの定義　＝相互相関関数

(I*K)(i,j) = \sum_m \sum_n I (i+m, j +m) K(m, n)
osn_Lofiosn_Lofi

Pix2Pix

** Conditional Gan**を画像から画像への変換の問題に応用したモデル

その名の通り、生成器と識別器に条件画像を入力する
（普通のGANにおいて、条件画像の入力はない。生成器には乱数のみ入力）
生成器は、乱数zと条件画像からスタイル変換を施した画像を出力する
識別器は、条件画像と生成器から生成した画像のペアから、そのペアが本物である確率を出力する。

L1ノルムの追加

通常のGANでは、識別器が本物と偽物を見分ける能力が向上するように目的関数を設計する。
しかし画像変換問題では、本物らしさだけでなく、入力画像と出力画像の一致具合を測る指標が別途必要となる。つまり、「条件画像と画像のペア」の一致度を保つための制約条件。
そこで、Pix2Pixでは識別器の損失関数にL1ノルムが加えられている。

L1ノルムを追加することで、画像の大域的な情報（全体的な構造）を捉えられるようになった＝つまり、低周波数の構造を良く捉えられるようになった。

PatchGanの採用

L1ノルムで低周波数の構造は捉えられるようになったが、高周波数の構造が捉えられない問題が残る。
これを解決したのがPatchGan。
画像の局所的なパッチの構造に注意を向けた。
パッチ径より離れた場所にあるピクセル間は独立であることを仮定して、識別器はN×Nのパッチが本物かどうかを判定するようにした。

生成器にU-Netを採用

生成器において、入出力画像間でエッジの位置の情報を共有する
→U-Netはエンコーダーとデコーダで情報を共有するから。
→ちなみに、情報の共有の仕方はチャンネルを連結する（和をとるではない）

osn_Lofiosn_Lofi

分散深層学習

データ並列

親モデルをコピーしたn個のレプリカ（子モデル）を各GPUワーカーに配置する
各GPUワーカーに異なるバッチを供給することで演算を並列化する

  • 同期型 は ** 非同期型**に比べてスループットが低い
  • 非同期型では、あるGPUワーカーが勾配を計算している間に、パラメータ更新が行われることがあるため、計算される勾配が古いパラメータに対して計算されることになる。これらの勾配を陳腐化された勾配と呼び、学習が不安定になることがある。
    →対策としては学習率を小さくすること

モデル並列

親モデルのn個の部分モデルを各GPUワーカーに配置する

osn_Lofiosn_Lofi

蒸留

大きなモデルが獲得した知識を小さなモデルに転移させることで、軽量化手法の一つ。
蒸留では、不正解クラスに対する確率を利用する

ソフトターゲット損失とハードターゲット損失

生徒を学習させる際、ソフトターゲット損失（L_soft)とハードターゲット損失(L_hard)を考える
ソフトとハードの加重平均値を最小化の対象とする

  • ソフトターゲット損失：先生の出力
  • ハードターゲット損失：正解ラベル

蒸留で用いるソフトマックス関数

温度Tを高くすることで、不正解に対する確率を大きくすることができる

Softmax(z) = \frac{\exp(z_i/T)}{\sum \exp(z_i/T)}

損失関数

Tの2乗をソフトターゲット損失にかけること

L = \frac{\lambda_1 T^2L_{soft} + \lambda_2 L_{hard}}{\lambda_1 + \lambda_2}
osn_Lofiosn_Lofi

ベルマン方程式の導出

収益の漸化式

すべてはここが出発点になる。導出は省略。難しい話ではない。
時点tにおける収益G_tについて、G_t+1を使って表しているだけ。

G_t = R_t + \gamma G_{t+1}

ちなみに黒本だR_t がR_t+1になっている

G_t = R_{t+1} + \gamma G_{t+1}

状態価値関数

状態S_tがsであるときの収益の期待値を状態価値関数として定義する

\nu_{\pi}(s) = \mathbb{E}[G_t | S_t =s]

収益の漸化式を状態価値関数に代入して整理する

E[X + Y ] = E[X] + E[Y]が成り立つため、

\nu_{\pi}(s) = \mathbb{E}[R_t | S_t =s] + \gamma \mathbb{E}[G_{t+1} | S_t =s]

上記式を第1項・第2項ごとにみていく
状態sで行動aを選択したとき状態s'に遷移して報酬rを受け取ることを想定する
エージェントの方策をπ（a|s)とする。
また環境の状態遷移を確率p(s' | s,a)で表す。
報酬はr(s, a, s')

第1項

\mathbb{E}[R_t | S_t =s] = \sum_{a,s'} \pi(a|s) p(s'|s, a)r(s, a, s')

第2項

状態価値関数を使って表す。

\mathbb{E}[G_{t+1} | S_t =s] = \sum_{a,s'} \pi(a|s) p(s'|s, a) \nu_{\pi}(s')

ベルマン方程式

Σπ（a|s)p(s'|s,a)が共通項で、報酬とs'の状態価値関数をくくっているだけ。

\nu_{\pi}(s) = \sum_{a,s'} \pi(a|s) p(s'|s, a) (r(s,a,s') + \gamma\nu_{\pi}(s'))
osn_Lofiosn_Lofi

音声認識

デジタル処理

  • 連続しているアナログ信号を離散的に変換する信号＝デジタル信号に変えること

サンプリング

  • コンピューターが信号を扱えるよう、1秒間に適当な個数だけデータを抽出すること
  • 1秒間に取り込むデータの数をサンプリング周波数という
  • サンプリング周波数が1,000Hzなら、1秒間に1,000個のデータを取得している
  • サンプリング周波数が大きいほど高音質となるが、データ量も増加する

サンプリング定理

  • 最大周波数の2倍以上の周波数で信号をサンプリングすると、元信号の連続波形を再現できる。
  • 入力信号の最大周波数が50Hzであれば、サンプリング周波数は100Hz以上にする必要がある。

ナイキスト周波数

  • サンプリングしたときに表現できいる、周波数の最大値をナイキスト周波数という。
  • サンプリング定理により、ナイキスト周波数は、サンプリング周波数の半分となる。
  • サンプリング周波数が100Hzなら、ナイキスト周波数は50Hzとなる。

フーリエ変換

  • あらゆる周期関数は正弦波の足し合せで表現できる特性を利用し、周波数成分に分解すること
  • 波形を三角関数の和で表していくこと

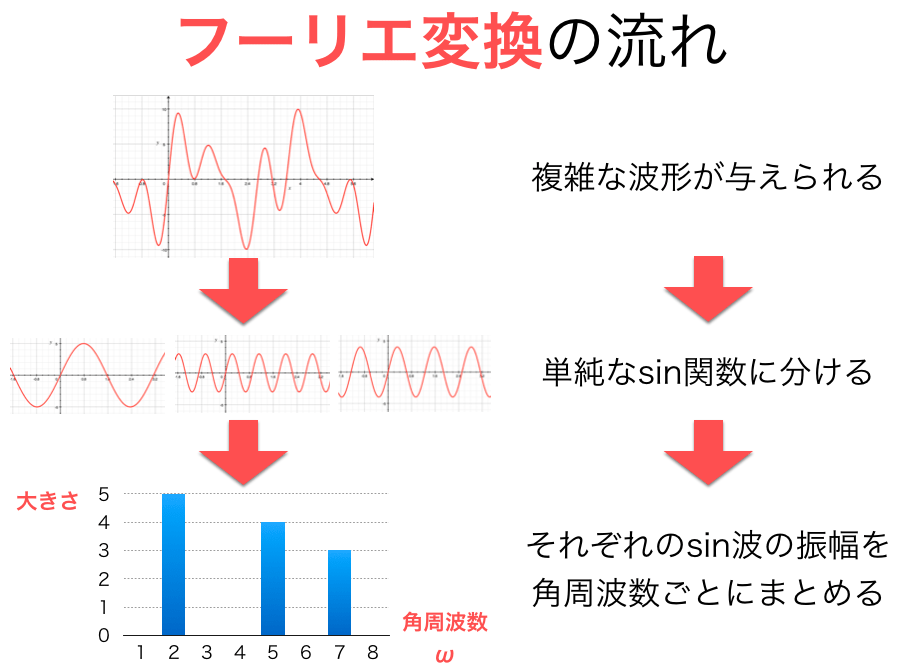
短時間フーリエ変換

  • フーリエ変換は時間領域全体に適用されるため、フーリエ変換後の周波数領域に時間情報がない。
  • 短時間フーリエ変換は時間領域を区間的にフーリエ変換する。それにより、時間変化する音声の分析が可能となる。
  • 短時間フーリエ変換後の値は「時間・周波数・振幅」の3次元になる
  • 音声を短時間フーリエ変換したものをスペクトログラムとよぶ。（右図）

https://qiita.com/shirowanisan/items/6af2cc4c4be0c57bef06

osn_Lofiosn_Lofi

GPT-n

Byte Pair Encording(BPE)

  • GPTのトークナイザーで使われているアルゴリズム
  • 単純な分かち書きではない
  • 高頻度の単語はそのまま、低頻度の単語は文字単位などの粒度で細かくわけていく

GPT-2とGPT-3の特徴

  • 事前学習は教師なし学習
  • ファインチューニングさえも行わない
  • 学習方法を学習するメタ学習を実現している
osn_Lofiosn_Lofi

尤度について考える

尤度とは、観測値X1、X2、・・・が与えられた時に、Xが従うと仮定した確率分布pの尤もらしさを求めにいく問題。

（例題）
10回くじを引いて、6回当たったとする。くじを1回引いた時の確率をpとしたとき、尤も確からしいp値はいくらか？

確率変数は、当たりの場合が1、ハズレの場合が0の2通りなので、単純なベルヌーイ分布。
尤度関数は、確率の積となるので

L(d) = \prod p^x = p^6 (1-p)^4

この尤度関数が最大になるpを推定する。
尤度関数は確率の積であるため、極めて値が小さいから、まず、対数をとる。
そして、最小化問題に変えるために、負にする。

-\log L(D) = -\log(p^6 (1-p)^4) = - ( 6\log p + 4 log(1-P))

微分したうえで＝0となるpを解く

- ( \frac{6}{p} -\frac{4}{1-p}) =0

pは3/5になる。これは結局、当たりの平均値と同じになる。

p = \frac{6}{10} = \frac{3}{5}

https://funatsu-lab.github.io/open-course-ware/basic-theory/likelihood/

osn_Lofiosn_Lofi

機械学習の基礎

機械学習の定義

Mitchell(1997)

コンピュータープログラムが、ある種のタスクTと性能指標Pにおいて経験Eから学習するとは、タスクTにおけるその性能を性能指標Pによって評価した際に、経験Eによってそれが改善されている場合である。

タスクとは・・・「何をしたいか」学習過程は含まれない

（例）
分類、回帰などの他に
欠損値のある入力の分類、構造出力、欠損値補完、ノイズ除去、密度推定

経験とは・・・

Mitchell

データ集合

Goodfellow

「機械学習アルゴリズムはデータ集合を経験する」

osn_Lofiosn_Lofi

マルチタスク学習

単一のモデルで複数の課題を解く機械学習の手法
転移学習はマルチタスク学習ではない

画像認識

物体検出やセマンティックセグメンテーションは、領域抽出とクラス分類の複数の課題を解いている

自然言語処理

形態素解析（係り受け・品詞づけ）、文意、文関係など複数の課題を同時に解いている

強化学習

本課題と補助課題を解いている

osn_Lofiosn_Lofi

オッズ比

ロジスティック回帰において、出力変数に対して、各入力変数がどれだけ影響を与えているかを測るもの。

事象が起きる確率をp、事象が起きない確率を（1ーp）とする。
ロジスティック回帰ではpと1-pは以下の通りに表すことができる

p= \frac{1}{1+\exp(-z)}
1-p= \frac{\exp(-z)}{1+\exp(-z)}

オッズ比は

オッズ比　= \frac{p}{1-p} = \exp(z)
osn_Lofiosn_Lofi

サポートベクトルマシン

ハードマージンSVM

線形分離可能な2クラス分類問題において、マージンの最大化を用いて解く
これだと線形分離不可能な問題を解くことができない

ソフトマージンSVM

スラック変数を導入することで、線形分離不可能な2クラス分類問題を解くことが可能。
マージン最大化とスラック変数にかかるペナルティ最小化を行う。

カーネルトリック

データをより高次元の空間に写像し、写像先の空間で識別面を決定する手法

osn_Lofiosn_Lofi

正則化

ラッソ

L_1(Lasso) = E + \lambda_1 ||w||_1

リッジ

L_2(Ridge) = E + \lambda_2||w||^2_2

エラスティックネット

Elastic Net = E + \lambda_1 ||w||_1 + \lambda_2||w||^2_2
osn_Lofiosn_Lofi
\underset{G}{min} \underset{D}{max} \mathbb{E}_x[\log D(x)] + \mathbb{E}_z[\log (1 - D(G(z)))]
osn_Lofiosn_Lofi

AdaGrad

h_{t+1} = h_t + \frac{\partial L}{\partial \theta_t} \bigodot \frac{\partial L}{\partial \theta_t}
\theta_{t+1} = \theta_t - \eta \frac {1} {\sqrt{h_{t+1}} + \epsilon} \bigodot \frac{\partial L}{\partial \theta_t} 
for key in params.keys():
      self.h[key] += grads[key] * grads[key]
      params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) +1e-7)

RMSprop

h_{t+1} = \rho h_t + (1 - \rho) \frac{\partial L}{\partial \theta_t} \bigodot \frac{\partial L}{\partial \theta_t}
\theta_{t+1} = \theta_t - \eta \frac {1} {\sqrt{h_{t+1}} + \epsilon} \bigodot \frac{\partial L}{\partial \theta_t} 
for key in params.keys():
      self.h[key] *= self.decay_rate
      self.h[key] += (1- self.decay_rate) * grads[key] * grads[key]
      params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) +1e-7)
osn_Lofiosn_Lofi

窓関数を使わない場合、スペクトログラムにノイズが現れる
スペクトル包絡
MFCCの低次成分はスペクトル包絡を表す
周波数スペクトルの緩やかな変動のこと

フォルマント→特徴
スペクトル包絡における周波数のピークのこと

フォルマント周波数
フォルマントに対応する周波数
フォルマント周波数に音素の特徴が現れる

スペクトル包絡には母音の特徴がでやすい
スペクトル包絡の時間方向の変化には子音の特徴が出やすい

メル→人間の尺度に合わせに行っている

古典的な音声認識では 隠れマルコフモデル が用いられる