✂️
ニューラルネットワークのPruningについてまとめてみた

2025/05/12に公開
 PruningとはPruning（枝刈り）は、ニューラルネットワークにおいて重要度の低いパラメータ（重みやノード）を削除することで、モデルをスリム化する手法です。削除されるのは、学習済みのネットワークにおいて出力への影響が小さいと判断された構成要素であり、その判断には様々な基準や手法が存在します。

本記事では、Pruningの種類や設計の要素について、MIT 6.5940の内容を基に整理します。

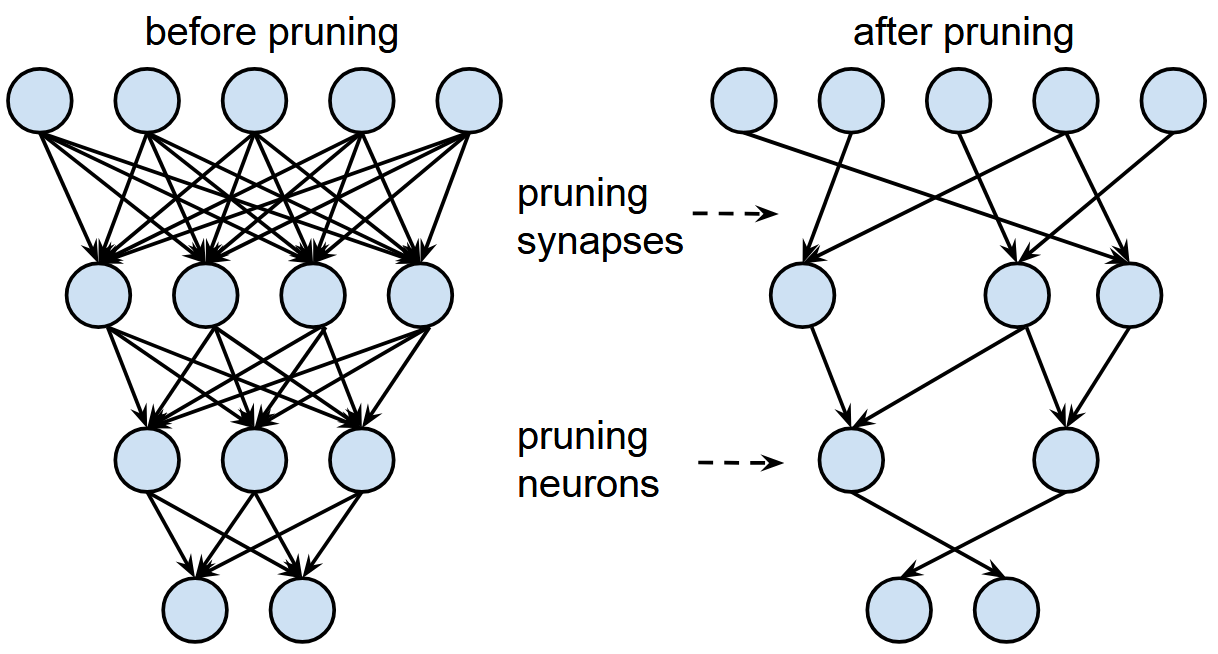
Learning both Weights and Connections for Efficient Neural Networks [Han et al., 2015]
なお、正確性には十分気をつけていますが、筆者はプロフェッショナルではないので間違いを含んでいる可能性があることをご了承ください。

 なぜPruningが必要か近年のディープニューラルネットワークは、性能向上を追求するあまり、パラメータ数・モデルサイズともに急速に増大しています。例えば、Llama 3.1 405Bモデルでは、FP8形式であっても推論時に約405GBのメモリを要するとされています。一方、ハイエンドGPUであるNVIDIA A100で80GB、H200でも141GBの容量しかなく、単一GPUでの推論は困難になりつつあります。

加えて、モバイル端末や組み込みデバイスのような計算資源が限られた環境では、大規模モデルをそのままデプロイすることは現実的とは言えません。

このような背景のもと、モデルのサイズや計算負荷を削減しながら、可能な限り性能を維持するための手段として、Pruningが注目されています。

 Pruningの手順Pruningは、一般的に以下の手順に従って行われます。

モデルの事前学習：まずは通常の方法でモデルを学習する。この段階では一切パラメータを削減せずに、モデル性能を最大化させることを目指す。

Pruning対象の決定/実行：重要度の低いパラメータを選別し値を0に置き換える。選別する粒度・基準は後述。

Fine-tuningの実施：Pruningによって性能低下を引き起こす場合があるので、Pruning後のネットワークを再学習する。一般的に、最初から学習するよりはFine-tuningを行ったほうが性能は良くなる。

 Pruningの粒度ここからは、Pruning対象をどのように決定するかを見ていきます。

Pruningの粒度(granularity)とは、どの単位でパラメータを削減するかを示す概念です。粒度が細かいほど個々のパラメータ単位での削除、粗いほど構造単位での削除となります。以下に代表的な粒度を示します。

 Fine-grainedこれは非構造化Pruningとも呼ばれています。この粒度では個々の重み単位でPruningを実行します。非常に柔軟性が高いためより多くのパラメータの削除が可能な一方、パターン化された削除方法ではないためハードウェアアクセラレーションを行うことは難しいとされています。

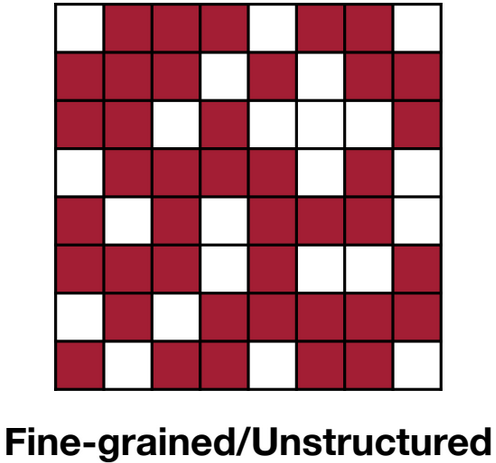
MIT 6.5940が作成

 構造化Pruning構造化されていないFine-grained Pruningは柔軟にパラメータを削減できる一方で、その不規則な削減パターンが原因で、ハードウェアアクセラレーションとの相性が悪いという課題がありました。限られた計算資源で効率的にモデルを構築するには、ハードウェアに最適化された手法を選ぶことが望ましいと言えます。

これに対して構造化Pruningでは、パターン単位、ベクトル単位、カーネル単位、チャンネル単位など、あらかじめ決められた構造に従ってパラメータを削除することで、ハードウェア側での最適化を可能にします。本記事ではこの中から、特に「パターンに基づく方法」と「チャンネル単位の方法」の2つを紹介します。なお、ベクトル単位やカーネル単位の方法はこれらに類似したバリエーションのため、今回は説明を省略します。

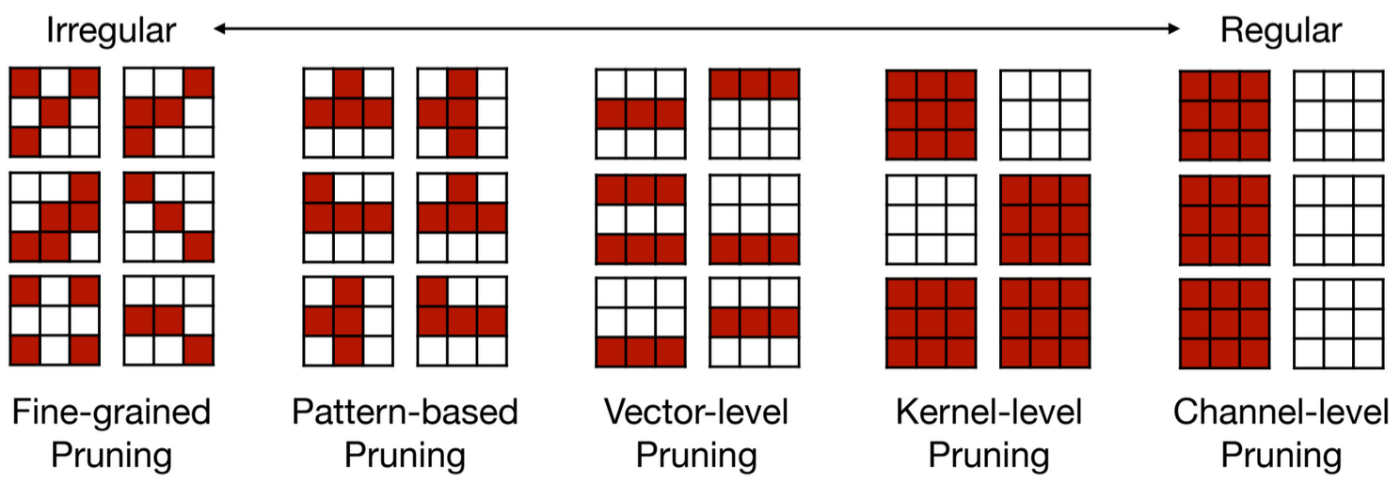
Mao et al., 2017をもとにMIT 6.5940が作成
この図の見方

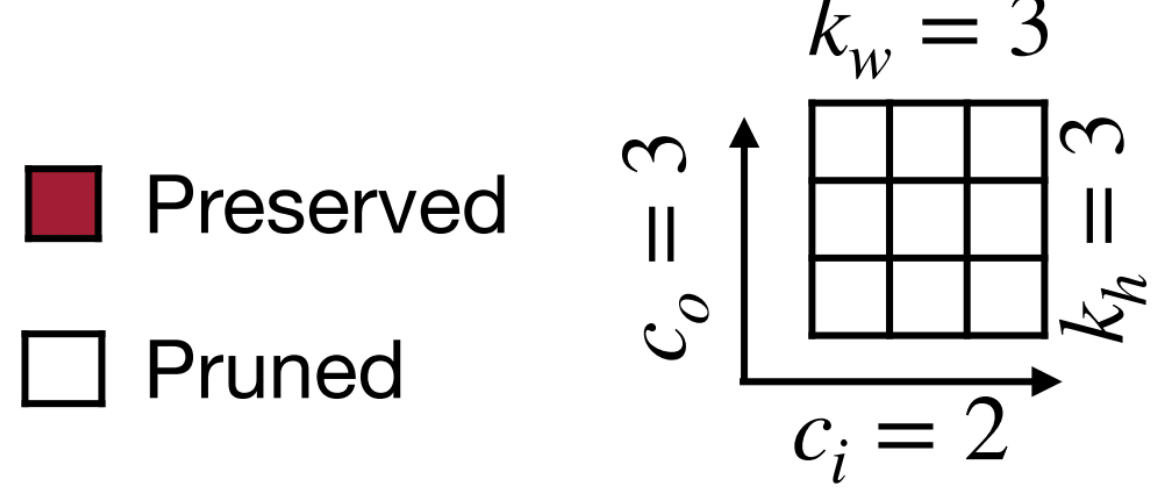
MIT 6.5940が作成

 パターンに基づく方法この方法では特定のパターンに沿ってPruningを実行します。ここでは代表的な手法である「M:N Sparsity」を紹介します。

 N:M Sparsityこれは連続するM個の要素のうち、N個をPruningする方法です。

下の図は2:4 Sparsityの例を示しています。連続する4つのパラメータのうち2つのパラメータを削除し、重み行列を圧縮しています。一番右に紫の行列が示されていますが、これは0になった重みがどこに位置していたのかを示す、2bitのインデックスです。

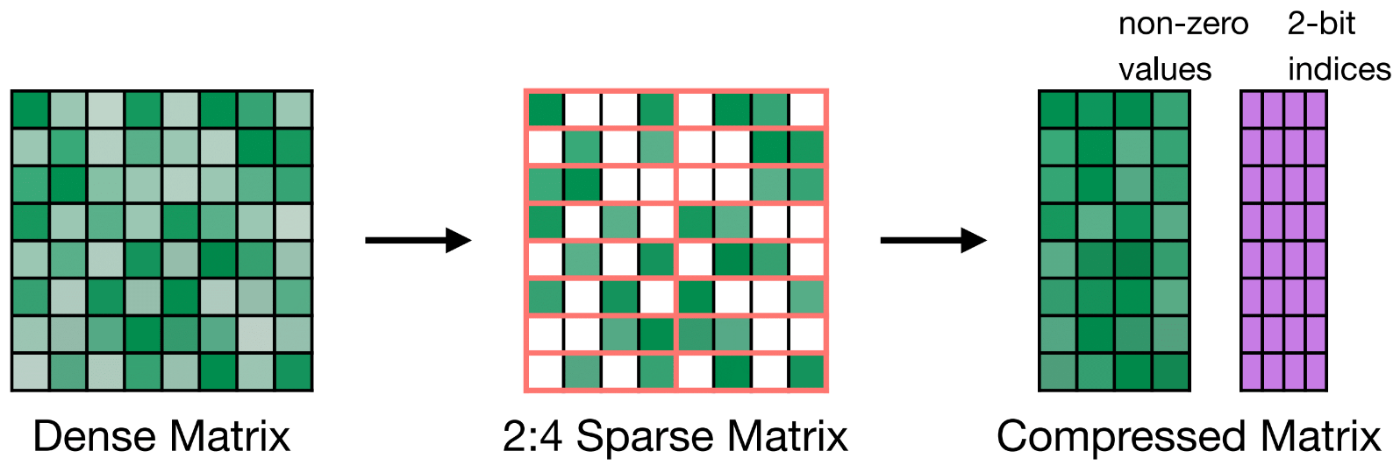
Accelerating Inference with Sparsity Using the NVIDIA Ampere Architecture and NVIDIA TensorRT
この手法は適切な再学習の実施により、Pruning前と同等の精度を維持できることが示されています。

また、NvidiaのAmpere以降のGPU（A100等）では2:4 Sparsityをハードウェアサポートしています。

 チャンネル単位の方法チャンネル単位のPruning（Channel Pruning）は、構造化Pruningの中でも広く利用されている手法の1つであり、特に畳み込み層において効果的です。この手法では、各畳み込み層の出力チャンネル単位で不要なチャンネルを選別・削除します。

出力チャンネルを削除すると、それに対応するカーネル（フィルタ）全体も不要になるため、計算量削減が明確に現れます。たとえば、1つのチャンネルを削除することで、そのチャンネルに対するすべての重み行列とバイアス、さらにその後続の層の入力次元も削減できます。

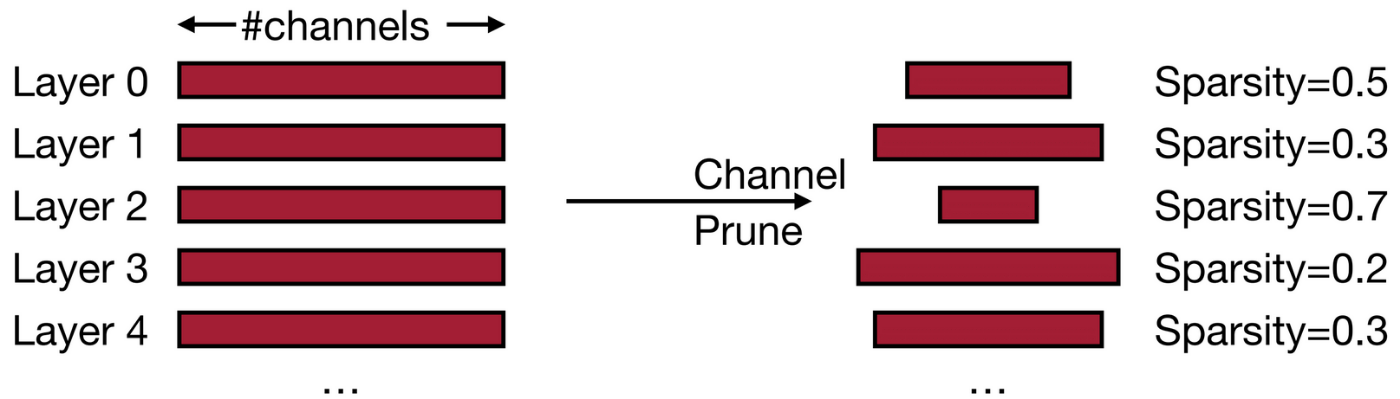
MIT 6.5940が作成。層ごとに異なるPruning率を設定する方法は後述

 Pruningの基準ここまでは、Pruningをどのような粒度で実行するかに注目してきました。しかし、実際にどの重みやチャンネルを削除するかを決定するには、それを選別するための基準（Criterion）も重要です。Pruningの効果を最大限に引き出すためには、適切な基準に基づいて対象を選ぶ必要があります。

本章では以下の代表的な基準を紹介します。
シナプスの選択方法
Magnitude-based
Scaling-based
Second-order-based

ニューロンの選択方法
Percentage-of-zero-based
Regression-based

 Magnitude-basedこの基準はヒューリスティックな方法で、「絶対値の大きな重みは重要な重みだろう」という洞察に基づいています。

各パラメータごとにこの基準を適用する場合、以下のようになります。

MIT 6.5940が作成
また、行ごとに行う場合の例を以下に示しています。行ごとにL1-norm（またはL2-norm）を行うことによって、どの行をPruningするか決定していることが示されています。

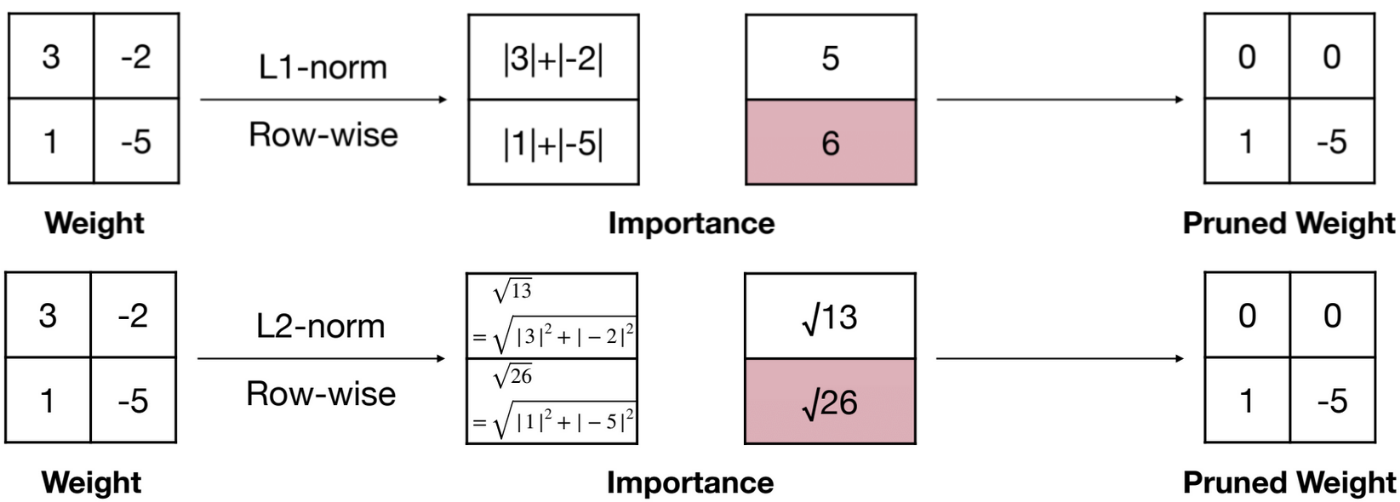
MIT 6.5940が作成

 Scaling-basedhttps://arxiv.org/abs/1708.06519
スケーリングに基づく方法は、ネットワークのスケーリング係数を指標として、各構成要素（チャンネルやノードなど）の重要度を評価し、削除するべき部分を決定するアプローチです。代表的な手法にはBatchNormのスケール係数を活用した方法があります。

BatchNorm層の出力は以下の式で表されます。

y_i = \gamma \cdot \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} + \beta
ここで、\gamma はスケール係数で、各出力チャンネルごとに学習されるパラメータです。

この \gamma の大きさが小さいほど、そのチャンネルの出力が抑えられており、出力に対する寄与が少ないと考えられます。したがって、小さい \gamma を持つチャンネルを削除対象としてPruningします。

 Second-order-basedこの基準は、損失関数の2階微分（ヘッセ行列）を活用して、パラメータの削除による影響を推定するアプローチです。

これまで紹介したPruning基準は、重みの絶対値などを使って重要度を評価しますが、パラメータ削除による出力の変化を考慮していませんでした。一方、Second-order-basedの代表例であるOptimal Brain Damage [LeCun et al., 1989]では次のような式に基づいて削除による影響を推定します。

\text{Saliency}(w_i) \approx \frac{1}{2} H_{ii} w_i^2

H_{ii} は 誤差関数のヘッセ行列の対角要素（2階微分）

w_i は対象の重み
式の導出方法重み w_i を0にした際、損失関数 E(\mathbf{w})がどれだけ増えるかを見積もります。

\Delta E = E(\mathbf{w}_{\setminus i}) - E(\mathbf{w})
つまり、削除による損失の変化をテイラー展開で近似します。

損失関数 E(\mathbf{w}) を現在の重みベクトル \mathbf{w} のまわりで2次のテイラー展開すると以下のようになります。

E(\mathbf{w} + \Delta \mathbf{w}) \approx E(\mathbf{w}) + \nabla E(\mathbf{w})^T \Delta \mathbf{w} + \frac{1}{2} \Delta \mathbf{w}^T H \Delta \mathbf{w}

\nabla E(\mathbf{w})：勾配ベクトル（1階微分）

H：ヘッセ行列（2階微分の行列）

\Delta \mathbf{w}：重みの変化（今回は w_i \to 0 の変化）
学習後のモデルでは、損失関数の勾配は0に近い（十分に収束している）と仮定します。

\nabla E(\mathbf{w}) \approx 0
これにより、テイラー展開の1次項は無視できて、以下が残ります。

\Delta E \approx \frac{1}{2} \Delta \mathbf{w}^T H \Delta \mathbf{w}
重み w_i だけを削除（=0に設定）するので以下のようになります。

\Delta w_j =
\begin{cases}
-w_i & (j = i) \\
0 & (j \neq i)
\end{cases}
\Rightarrow \Delta \mathbf{w} = (0, ..., -w_i, ..., 0)

\Delta E \approx \frac{1}{2} H_{ii} w_i^2
ここで H_{ii} はヘッセ行列の対角成分（つまり \frac{\partial^2 E}{\partial w_i^2}）です。
よって、重み w_i を削除したときの誤差増加量の近似は以下のようになります。

\text{Saliency}(w_i) \approx \frac{1}{2} H_{ii} w_i^2
この式から、損失への影響が小さくなるような重み（重みが小さい+損失の曲率が小さい）を選んで削除する、というのが基本方針です。

 Percentage-of-zero-basedhttps://arxiv.org/abs/1607.03250
出力における0の割合が高いチャンネルを削除する方法です。

0の割合（Average Percentage of Zeros）は以下の式で計算されます。

APoZ^{(i)}_c = \frac{ \sum_{k=1}^N \sum_{j=1}^M f(O^{(i)}_{c,j}(k) = 0) }{N \times M}

i：レイヤー番号

c：チャンネル番号

N： バリデーションデータの総数

M：各出力の空間次元

O^{(i)}_{c,j}(k)：サンプル k に対するレイヤー i のチャンネル c の出力の j 番目の要素

f(\cdot)：条件が真なら1、偽なら0を返す関数（indicator関数）
図として表すと以下のようになります。

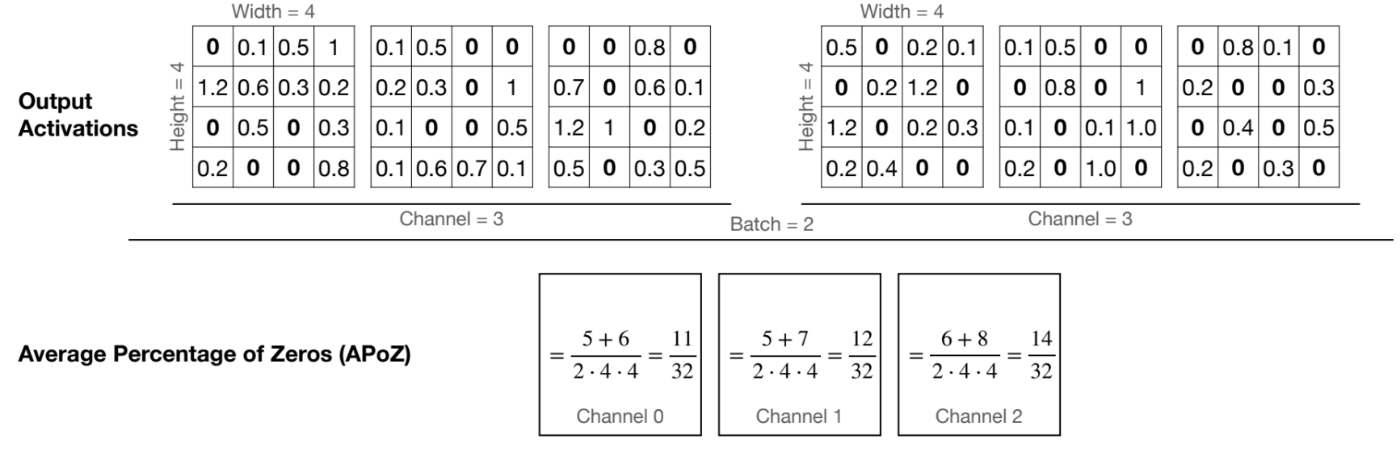
MIT 6.5940が作成
「レイヤー i にあるチャンネル c の出力がゼロになる割合を、全バリデーションデータと全空間位置について平均したもの」がAPoZと言えるでしょう。

 Regression-based回帰（Regression）を用いたPruningは、削除するパラメータの選択を誤差の予測という観点から最適化するアプローチです。これは「削除によってどれほどモデルの出力が変化するか」を定量的に評価し、出力への影響が最小になるようなパラメータを選択する点が特徴です。

この手法は、He et al. (2017) によって提案された Channel Pruning via Mean Squared Error Minimization に基づいています。

まず、ある層の出力を次のように表現します。

\mathbf{Z} = \sum_{c=0}^{c_i-1} \mathbf{X}_c \mathbf{W}_c^\top

\mathbf{X}_c：入力テンソルのチャンネルc

\mathbf{W}_c：チャンネルcに対応するカーネル

\mathbf{Z}：層の出力
ここで、Pruning後の出力を \hat{\mathbf{Z}} とし、Pruningによってもとの出力とできるだけ変わらないようにしたいという目標を、以下のような最適化問題として定式化します。

\arg\min_{\mathbf{W},\,\boldsymbol{\beta}} \left\| \mathbf{Z} - \sum_{c=0}^{c_i - 1} \beta_c \mathbf{X}_c \mathbf{W}_c^\top \right\|_F^2
ここでの変数は次のような意味を持ちます。

\boldsymbol{\beta} \in \{0,1\}^{c_i}：チャンネルごとの選択を表すベクトル。\beta_c = 0 でチャンネルcを削除する。
制約 \left\| \boldsymbol{\beta} \right\|_0 \le N_c：残すチャンネル数の上限を定める（非ゼロの数がN_c以下）

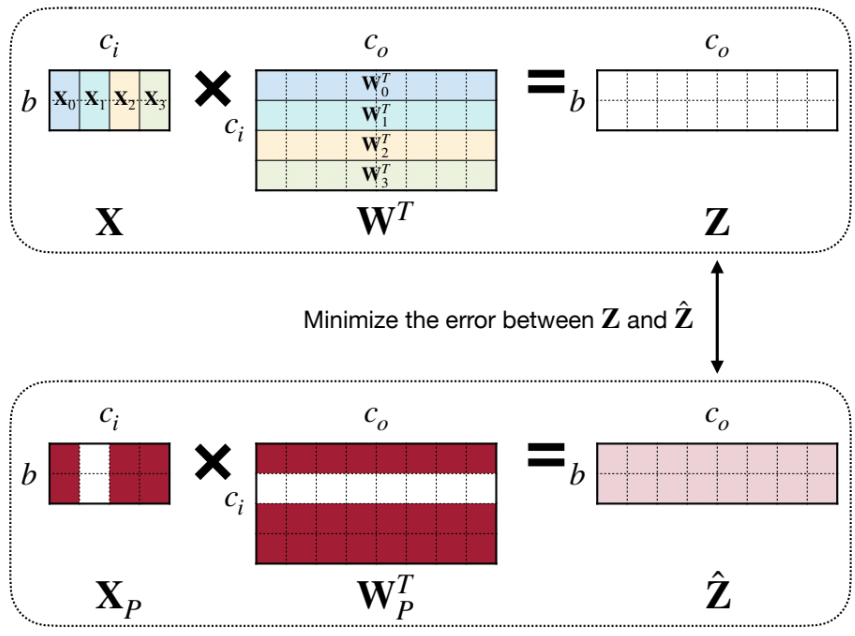
MIT 6.5940が作成
この手法の本質は、チャンネルを削除しても出力ができるだけ変化しないようにするという考え方にあります。単純なL1ノルムなどの指標ではなく、「出力空間における影響度」に基づいて削除対象を選ぶため、精度劣化を抑えやすいという利点があります。

 層ごとのPruning率の最適化ここまで、Pruningの粒度（どの単位で削減するか）と基準（どのパラメータを削減するか）について見てきました。しかし、どの程度まで削減するか（Pruning率）も、モデル性能や推論効率に大きく影響する重要な要素です。

たとえば、チャンネル単位の構造化Pruningにおいて、すべての層に一律のPruning率を適用するのではなく、層ごとの特性に応じて異なる割合でPruningを行います。これにより高い精度を維持しつつ、推論時のレイテンシを抑えることが可能になります。

しかし、層ごとにどの程度Pruningを行うべきかを事前に知ることは困難です。層によってモデル全体の性能に与える影響度は異なるため、一律の基準では最適なPruning率を見つけられないのが実情です。

 Sensitivity Analysis各層に対して一律のPruning率を設定する方法では、ネットワーク全体の性能を最適化することは困難です。なぜなら、層ごとに表現している情報の重要度やロバスト性が異なるため、同じ割合でパラメータを削減しても、ある層では性能にほとんど影響がない一方、他の層では致命的な劣化を引き起こす場合があるからです。

このような状況に対して有効なアプローチのひとつが、感度分析（Sensitivity Analysis）です。感度分析では、各層ごとに異なるPruning率を段階的に適用し、それによって生じる性能指標（通常は精度や損失）の変化を測定します。このとき、以下のようなステップで進行します。

層単位でのPruning実験：各層に対して単独で一定割合のPruningを施し、その都度全体の推論精度を測定する。例えば、層Xを10%, 20%, …, 90% の割合でPruningして、その精度を記録する。

感度スコアの評価：精度の劣化度合いを基に、各層の性能への寄与度（＝感度）を定量化する。例えば、「80%削除しても精度がほとんど変わらない層」は感度が低く、「20%削除するだけで精度が大きく落ちる層」は感度が高いとみなす。

Pruning率の最適化：得られた感度に基づいて、感度の低い層から優先的に高いPruning率を適用し、感度の高い層にはより慎重にPruningを行う戦略を構築する。これはヒューリスティックに設定する場合もあれば、最適化問題として定式化し解を求めることもある（例：Lagrangianベースの最適化など）。

MIT 6.5940が作成

 AMC (AutoML for Model Compression)従来の感度分析ベースのPruning手法では、各層を個別に評価し、それぞれに適切なPruning率を割り当てる設計が主流でした。しかしこのアプローチでは、層間の相互作用（例：前層の出力が後層の入力に影響する構造）を無視しており、全体として最適なネットワーク設計にはならない可能性があります。さらに、ネットワーク全体におけるPruning率の探索は膨大な組み合わせを持つため、手動による設計やグリッドサーチでは非現実的です。

AMC [He et al., 2018]は、深層モデルのPruning率の決定を自動化された最適化問題として定式化し、強化学習を用いてその解を探索する手法です。

AMCでは、モデル圧縮を「逐次的な意思決定問題」として定式化し、強化学習の枠組みで各層のPruning率を段階的に決定するエージェント（ポリシー）を学習します。主な構成は以下のとおりです。

State：現在の層に関する情報

Action：その層で適用するPruning率

Reward：最終的な精度とFLOPに基づいて計算（−\text{Error} \times \log{(\text{FLOP})}）

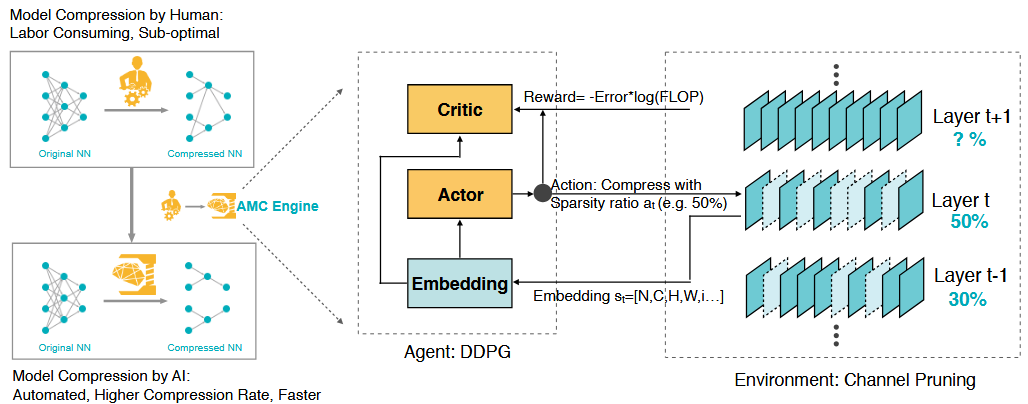
AMC: AutoML for Model Compression and Acceleration on Mobile Devices [He et al., 2018]
学習の流れとしては、ポリシーネットワーク（DDPG）を用いて層ごとのPruning率を逐次的に選択し、それに基づいて生成された圧縮済みモデルを評価し、報酬をフィードバックしてポリシーを更新します。

AMCは人間では1週間かかる作業を数時間で実施できます。

AMC: AutoML for Model Compression and Acceleration on Mobile Devices [He et al., 2018]
また、実験では性能を維持しながらレイテンシとメモリ使用量を改善できることを示しました。

 モデルのFine-tuningPruning後のモデルは性能低下を引き起こす場合があるため、Fine-tuningによって精度を回復する必要があります。

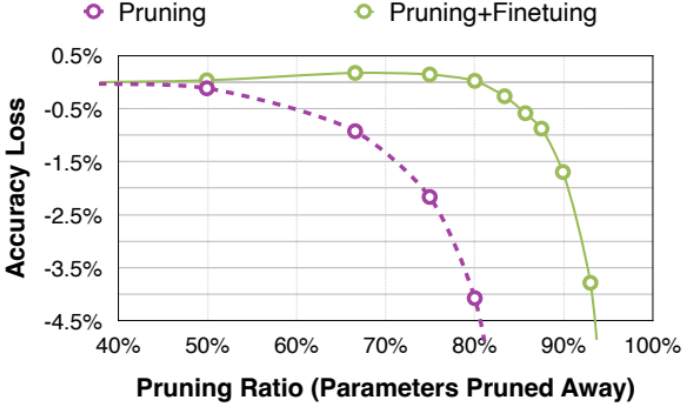
MIT 6.5940が作成

 Iterative Pruninghttps://arxiv.org/abs/1506.02626
Pruningを実施する際、一度に大きな割合のパラメータを削除してしまうと、モデルの性能が急激に低下してしまうことがあります。Iterative Pruning（反復的Pruning）は、少しずつ段階的にパラメータを削減し、そのたびに再学習（ファインチューニング）を行うことで、性能を維持しながら圧縮を進める手法です。

Iterative Pruningでは、以下のような手順でPruningが進行します。
モデルを初期学習または事前学習済みモデルから開始
Pruning基準に基づいて一部のパラメータを削除
削減後のモデルをファインチューニングして精度を回復
再びPruning → ファインチューニングを繰り返す
目標のPruning率または精度低下のしきい値に達したら停止
この「Pruning → ファインチューニング」のループを数回繰り返すことで、急激な性能劣化を回避しながら高い圧縮率を達成できます。

MIT 6.5940が作成

 おわりに本記事では、ニューラルネットワークのモデル圧縮手法として広く研究されているPruningについて、基本的な概念を整理しました。

近年のモデルはますます大規模・高性能化している一方で、リソース制約のある環境や実運用の観点からは、軽量かつ効率的なモデルが求められる場面も少なくありません。Pruningはそのようなニーズに応えるための重要な技術のひとつであり、適切に設計・適用することで、モデルの性能を維持しつつ計算資源の節約や高速化を実現可能です。

Pruningの設計は「どこを」「どのように」「どのくらい」削減するかという多面的な選択が絡むため、単純なルールだけでなくモデルや目的に応じた柔軟なアプローチが必要です。今後、さらなる自動化技術やハードウェアとの協調設計が進む中で、Pruningの研究と実装はますます重要性を増していくでしょう。

本記事が、Pruningの理解を深める一助となれば幸いです。