0から作るDeepな推薦システム ~Matrix Factoization~
はじめに
推薦システムの古典的な手法にMatrix Factorizationというものがあります。
本記事ではMovielensという映画レビューのデータセットを使って、pytorchでMatrix Factorizationを使った推薦システムを実装しようと思います。
Notebook実装・Githubの実装はこちらです。
Matrix Factorization概要
推薦システムのタスクの一つに「ユーザの評価を予測する」というものがあります。
ユーザにある商品をレコメンドしたくても、ユーザの好みが分からなければどの商品をレコメンドすべきかが分かりません。
そこでMatrix Factorizationでは、これまでのユーザ x アイテムの評価値をもとに未知のアイテムを予測する、ということを行います。

上の画像だと、User-Home Matrixの一番左上(青いユーザの青の家に対する好み)のマスを予測するためには、User Matrixの青いユーザの特徴とHome Matrixの青い家の特徴の内積を取ることで計算します。
この例だと0.24 x 1.5 + 0.16 x 1.7 = 0.632という値が推測された評価値になります。
特徴行列の次元は自由に設定することができ、上の場合だと2次元でそれぞれの特徴行列を表現しています。
では、どうやってユーザとアイテムの特徴行列を作成するのかというと、すでに得られているユーザの評価をもとに、行列積の値が評価値に近づくようにそれぞれの特徴行列を作成します。
流れとしてはこんな感じです。
- ユーザー・アイテムの特徴行列をランダムに設定
- 特徴行列同士の行列積をとってユーザxアイテムのの評価値を計算
- 計算された評価値と実際の評価値の誤差をもとに特徴行列を修正
Pytorchによる実装
一部のコードについて説明します。詳細なコードは実装をご覧ください。
データセットのダウンロード
以下のようにMovieLens-1mのデータをダウンロードします。
!wget https://files.grouplens.org/datasets/movielens/ml-1m.zip
!unzip ml-1m.zip
ダウンロードしたデータには、movies.dat、ratings.dat、users.datが含まれていますが、今回は、ユーザと映画の評価の情報が含まれている、raitings.datを利用します。
内容はこちらのように、あるユーザの映画に対する1~5の評価が記録されたものとなっています。
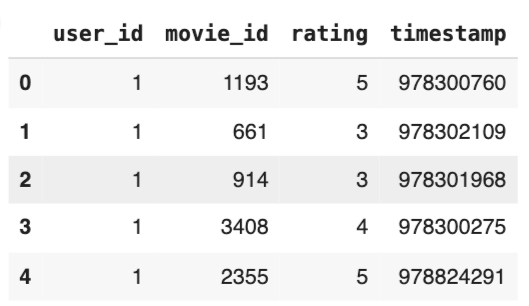
データセットの作成
続いてデータセットを作成していきます。
movielensのデータセットを読み込んで、ユーザのid、映画のid、評価値を取得します。
class MovilensDataset(Dataset):
def __init__(self, df):
self.df = df
self.users = df.user_id.values
self.items = df.movie_id.values
self.ratings = df.rating.values
def __len__(self):
return len(self.df)
def __getitem__(self, idx):
user_id = self.users[idx]
movie_id = self.items[idx]
ratings = self.ratings[idx]
return {
"users": torch.tensor(user_id, dtype=torch.long),
"movies": torch.tensor(movie_id, dtype=torch.long),
"ratings": torch.tensor(ratings, dtype=torch.float),
}
モデルの作成
作成したモデルはこちらのようになっています。
特徴行列は、nn.Embedingを利用して、ユーザ数 x 潜在次元、アイテム数 x 潜在次元の行列を作成しています。
ここではpytorchのnn.Embedingを利用して特徴行列を作成しています。
ユーザとアイテムの特徴行列に加えて、それぞれのバイアス項を用いて評価値を計算しています。
バイアス項により、ユーザーやアイテムの個別の影響(たとえば、特定のユーザが全体的に高評価をつけやすいか、あるいは特定のアイテムが他より好まれやすいか)を捉えることができます。
class MatrixFactorization(nn.Module):
def __init__(self, num_users, num_items, num_factors):
super().__init__()
self.user_emb = nn.Embedding(num_users, num_factors)
self.item_emb = nn.Embedding(num_items, num_factors)
self.user_bias = nn.Embedding(num_users, 1)
self.item_bias = nn.Embedding(num_items, 1)
def forward(self, user_id, item_id):
user_feats = self.user_emb(user_id)
item_feats = self.item_emb(item_id)
user_bias = self.user_bias(user_id)
item_bias = self.item_bias(item_id)
outputs = (user_feats*item_feats).sum(1) + torch.squeeze(user_bias) + torch.squeeze(item_bias)
return outputs
モデルの学習
実際に特徴行列の学習をしていきます。
モデルの出力がそのままユーザxアイテムの評価値の予測になっているので、その値と実際の評価値の誤差からユーザとアイテムの特徴行列を更新していきます。
損失関数は平均二乗誤差(nn.MSELoss)、最適化関数はSGDを利用しています。
lr = 5e-4
wd = 1e-5
epochs = 10
criterion = nn.MSELoss(reduction="sum")
optimizer = torch.optim.SGD(model.parameters(), lr=lr, weight_decay=wd)
train_loss_log = []
valid_loss_log = []
for epoch in range(epochs):
model.train()
train_running_loss = 0.0
for batch in train_dataloader:
user_ids = batch["users"].to(device)
item_ids = batch["movies"].to(device)
ratings = batch["ratings"].to(device)
outputs = model(user_ids, item_ids)
optimizer.zero_grad()
loss = criterion(outputs, ratings)
loss.backward()
optimizer.step()
train_running_loss += loss.item()
model.eval()
with torch.no_grad():
valid_running_loss = 0.0
for batch in valid_dataloader:
user_ids = batch["users"].to(device)
item_ids = batch["movies"].to(device)
ratings = batch["ratings"].to(device)
outputs = model(user_ids, item_ids)
loss = criterion(outputs, ratings)
valid_running_loss += loss.item()
train_loss = train_running_loss / train_size
valid_loss = valid_running_loss / valid_size
train_loss_log.append(train_loss)
valid_loss_log.append(valid_loss)
print(f"[epoch {epoch+1}] train loss: {train_loss:.5f} valid loss: {valid_loss:.5f}")
学習結果
損失のグラフはこんな感じです。
しっかり損失も下がっていますね!

最後に学習した埋め込みベクトルの確認をしてみます。
先ほどの図のように、Matrix Factorizationでは評価値行列からユーザとアイテムの特徴ベクトルの生成をします。
そして、似ているアイテムであれば、それらの特徴ベクトルの同士の類似度は高くなることが予想されます。

Movielensのデータから、トイストーリー・スターウォーズ5・スターウォーズ6の特徴ベクトルを利用してcos類似度がどうなっているかをを確認してみます。
まず、これらの映画のIDの確認をします。

そして、モデルのアイテム埋め込みの部分から特徴ベクトルを取得してcos類似度を確認します。
toystory_id = 1
starwars5_id = 1196
starwars6_id = 1210
toystory_label, starwars5_label, starwars6_label = le_movie.transform([toystory_id ,starwars5_id, starwars6_id])
toystory_emb = model.item_emb(torch.tensor(toystory_label).to(device))
starwars5_emb = model.item_emb(torch.tensor(starwars5_label).to(device))
starwars6_emb = model.item_emb(torch.tensor(starwars6_label).to(device))
print(f"Toy StoryとStarWars VのCOS類似度 : {F.cosine_similarity(toystory_emb, starwars5_emb, dim=-1):.4f}")
print(f"Toy StoryとStarWars VIのCOS類似度 : {F.cosine_similarity(toystory_emb, starwars6_emb, dim=-1):.4f}")
print(f"StarWars VとStarWars VIのCOS類似度 : {F.cosine_similarity(starwars5_emb, starwars6_emb, dim=-1):.4f}")
結果はこちらになります!
なんともいえない感じですが、確かにStarwars同士の類似度が高いことが確認できますね。
Toy StoryとStarWars VのCOS類似度 : 0.4508
Toy StoryとStarWars VIのCOS類似度 : 0.2202
StarWars VとStarWars VIのCOS類似度 : 0.6804
まとめ
PytorchでMatrix Factorizationの実装、学習を行い損失が下がっていること、そして実際の特徴ベクトルの値を確認して似ているアイテムの類似度が高いことを確認しました。
Reference
本記事を書くにあたり、以下の記事を参考にしました。
Discussion