Kyulacsを使って量子機械学習を実行してみた。
Kyulacsって?
量子回路シミュレータqulacsをjuliaの型でラップした野良パッケージです。juliaで量子計算をしたいんじゃ!みたいな人には使えるかと思います。
なぜjuliaの型でラップするのか、マクロを使うメリットは?
python関数をjulia側の型でラップすることで、エラーハンドリングがjulia側で行えると言う利点があるからです。 pythonとは違ってjuliaでは関数の引数に型の指定などができますので、そのメリットを享受できることになります。
また、Kyulacsでは、マクロ機能を積極的に使うことで、かなり効率よくラップすることに成功しています。
私自身研究でqulacsをjulia側で呼び出して使っていたことがあったのですが、この時は、手作業でjuliaの型でqulacsの関数をラップしていましたので、関数をラップするのが面倒でした(当初はyao.jlとqulacsを共通のインターフェイスで実行するというもくろみがあったからです)。この点、Kyulacsでは、マクロ機能を使って自動でラップをしています。以下の解説記事にあるようにjuliaのマクロの強力さを実感することができるかと思います(これを作ったごまふあざらし氏に感謝です)。
実際に使ってみた感想と今後の期待など
本記事ではKyulacsの動作の確認をかねて、実際に量子機械学習を実行してみました。結論から言うと、qulacsと同じような使い心地で量子計算が実行できました。
2022/2/20時点ではqulacsのinner_productの関数はラップされていなかったので、直接pythonの関数を呼び出して使っています(2022/2/21にKyulacs.jlがアップデートがされて、
using Kyulacs.State とすると inner_product 関数が呼び出せるようになったので qulacs.state.inner_product と書かずに済むようになりました)。
今後GPUを使った計算などもjuliaでラップされることを期待です。
(2022/2/23にGPUもサポートされたみたいです。)
また、ループのインデックスの問題で、pythonは0始まりなのに対して、juliaでは1始まりです。ここらへんを擦り合わせる必要があります。もしくは、以下のようにpythonのrangeを使うと言う方法もあります。今回の例では2量子ビットしか使ってないのでこれでいいと思います。
using PyCall
pyrange = pybuiltin("range")
for i in pyrange(n)
# do something
end
実行例
まずは、上の記事にあるコードを参照し、以下を実行してみました。
using Kyulacs: Observable, QuantumCircuit, QuantumState, ParametricQuantumCircuit
using Kyulacs.Gate: CNOT, Y, merge
using Kyulacs: qulacs #wrapしていない関数を呼び出す。
state = QuantumState(3)
seed = 0 # set random seed
state.set_Haar_random_state(seed)
circuit = QuantumCircuit(3)
circuit.add_X_gate(0)
merged_gate = merge(CNOT(0, 1), Y(1))
circuit.add_gate(merged_gate)
circuit.add_RX_gate(1, 0.5)
circuit.update_quantum_state(state)
observable = Observable(3)
observable.add_operator(2.0, "X 2 Y 1 Z 0")
observable.add_operator(-3.0, "Z 2")
value = observable.get_expectation_value(state)
# 0.2835596510287872
println(value)
きちんと値が出力されましたので動作は確認できました。
Kyulacsを用いた量子機械学習の実行例
以下では、カーネル法に基づく量子機械学習を実行してみます。
問題設定は以下の通りです。
Ry(2x) を2量子ビットに作用させて得られる特徴量ベクトルを使って、量子カーネル法によって
をフィッテングによって再現する \sin^2(x)
当初の目的は、実際にKyulacsで比較的応用に近い量子計算が実行できるか調べたかったということなので、計算の詳細については触れていないです。今後時間があるときに書き足す予定です。本記事の最後に参考にしたURLを貼っておきましたのでそちらをご参照いただければと思います。
また、間違いなどありましたら、ご指摘いただけると幸いです。
import Pkg; Pkg.add("Plots")
Ry(2x) を2量子ビットに作用させる関数を用意します。
n_qubits = 2
function get_circuit(n_qubits::Int)
circuit = ParametricQuantumCircuit(n_qubits)
for i in 1:n_qubits
circuit.add_parametric_RX_gate(i-1, 0)
end
return circuit
end
上の量子回路に初期パラメータを代入する関数を用意します。
function set_input_to_circuit(x::Float64, circuit::ParametricQuantumCircuit)
circuit.set_parameter(0, 2*x)
circuit.set_parameter(1, 2*x)
end
ここで、juliaで今回再現する
using Random
using Plots
n_data = 32
X = collect(range(-pi ,pi, length=n_data))
y_clean = sin.(X).^2
y_noise = y_clean .+ randn(n_data) .* 0.1
#LatexString
# LaTeXString を使う
import Pkg; Pkg.add("LaTeXStrings")
using LaTeXStrings
p = plot(xlabel="X", ylabel="\$\\sin^2(X)\$")
plot!(p, X, y_clean, label="clean")
plot!(p, X, y_noise, seriestype=:scatter, seriescolor=:red, label="noise") # "scatter"でもOK #label=:noneで表示されない
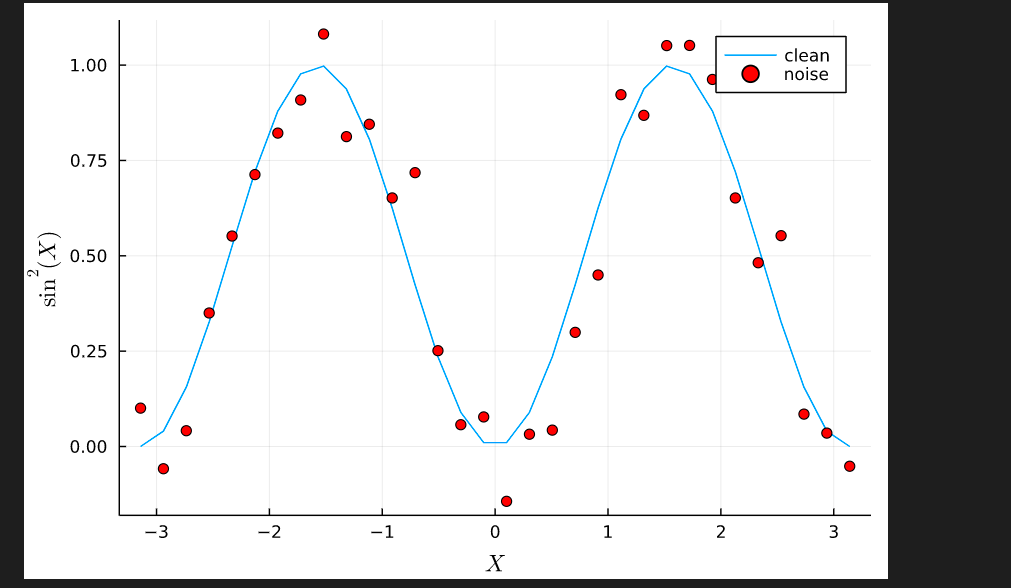
特徴量ベクトルを用意します
n_qubits = 2
circuit = get_circuit(n_qubits)
xs = collect(range(-pi, pi, length=32))
state = QuantumState(n_qubits)
feature_vector = [zeros(ComplexF64, size(xs)) for i in 1:2^(n_qubits)]
for i in 1:32
state.set_zero_state()
set_input_to_circuit(xs[i], circuit)
circuit.update_quantum_state(state)
vec = state.get_vector()
for (k, c) in enumerate(vec) # k, cを()デクくるのを忘れない
feature_vector[k][i] = vec[k]
end
end
カーネルの値を計算する関数を用意します。
# qulacs で内積を計算する関数
# from qulacs.state import inner_product
# 毎回メモリ確保すると遅いので、カーネルの計算用に量子状態・量子回路を準備しておく。
n_qubits = 2
_circuit = get_circuit(n_qubits)
_state1 = QuantumState(n_qubits)
_state2 = QuantumState(n_qubits)
# 関数本体
function get_kernel_value(x1::Float64, x2::Float64)
_state1.set_zero_state() #初期化
set_input_to_circuit(x1, _circuit)
_circuit.update_quantum_state(_state1) #x1に対応する状態を準備
_state2.set_zero_state() #初期化
set_input_to_circuit(x2, _circuit)
_circuit.update_quantum_state(_state2) #x2に対応する状態を準備
return qulacs.state.inner_product(_state1, _state2)
end
xj_list = [0.0, pi, pi/3, pi/3]
x1 = collect(range(-pi, pi, length=50))
# grid の各点で特徴量ベクトルの成分を計算し、保存する。
kernel_values = [zeros(ComplexF64, size(x1)) for i in 1:length(xj_list)]
for (index, xj) in enumerate(xj_list)
for i in 1:50
xi = x1[i]
kernel_values[index][i] = get_kernel_value(xi, xj)
end
end
カーネルを可視化してみます。
ps = []
for i in 1:length(xj_list)
p1 = plot(x1, abs.(kernel_values[i]))
push!(ps, p1)
end
plot(ps..., layout=(1,4), size=(800, 200)) #ps...でpsに入っている要素を全部並べたものに対応する。
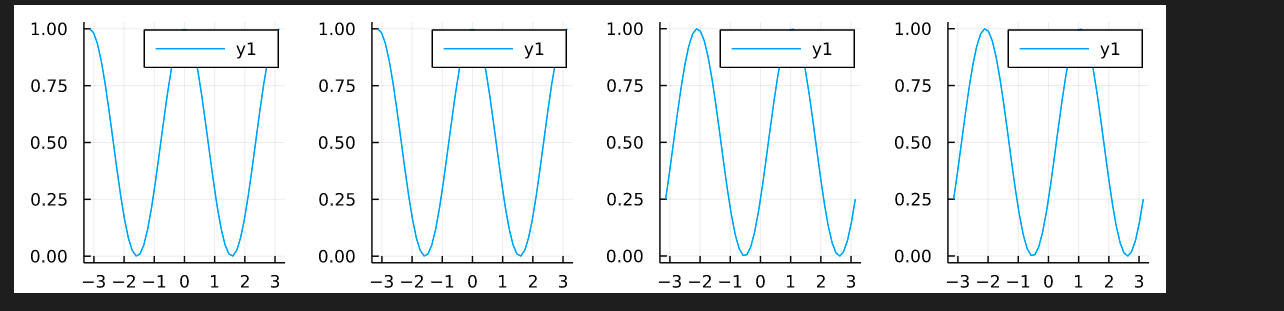
#%matplotlib notebook
using Random
state = QuantumState(n_qubits)
circuit = get_circuit(n_qubits)
function get_output_vector(x::Float64)
state.set_zero_state()
set_input_to_circuit(x, circuit)
circuit.update_quantum_state(state)
return state.get_vector()
end
n_data = 100
n_grid = 100
Random.seed!(100)
X = rand(n_data, 1) .*2 .* pi
y= sin.(X).^2 + randn(n_data) .* 0.1 #0で始まるものはbeginで置き換える。
plot(x -> sin(x)^2, xlim=(0.0, 2pi))
scatter!(X, y)
#size(X)

# 対角成分はすべて 1 なので最初から 1 で埋めておく。
gram_matrix = zeros(ComplexF64, n_data, n_data)
# 対称性を使って計算
for i in 1:n_data
gram_matrix[i,i] = 1.0
for j in 1:i-1
gram_matrix[i,j] = get_kernel_value(X[i], X[j]) #k(i,j)
gram_matrix[j,i] = conj(gram_matrix[i,j])
end
end
gram_matrix
regularization = 0.001
using LinearAlgebra
a = inv(gram_matrix .+ regularization .* I(n_data)) * (y)
#a_ = np.linalg.inv(gram_matrix + regularization*np.identity(n_data))
#l = y.T * a_
function predict(x::Float64)
k_vector = [get_kernel_value(x_train, x) for x_train in X]
return sum(a .* k_vector) #
end
#%matplotlib notebook
n_grid = 100
x_surface = collect(range(0, pi*2, length=n_grid))
#y_surface = np.zeros_like(x_surface)
predict_surface = zeros(ComplexF64, size(x_surface))
for i in 1:n_grid
predict_surface[i] = predict(x_surface[i])
end
plot(x -> sin(x)^2, xlim=(0.0, 2pi), label="clean")
scatter!(X, y, label="noise")
plot!(x_surface, real.(predict_surface), label="predict")
結果

まとめ
Kyulacsを使って量子計算が実行できることを確かめました。
補足
qulacsPythonAPIにある関数はラップされたみたいです。あとGPUもサポートするようになったようです。
参考
コードの詳細は、こちらを参照させていただきました。
Discussion
拝読しました!誠に有難うございます。