MPS形式でAx=bを解く（随時更新)

A,bがそれぞれMPO,MPSで与えられている時、

$$Ax = b$$

のxについて解く

MPSをMPOに直す

都合上、Cがb、xをBだと思ってください。

$$C(t) = A(t) B(t)$$

binary coding

$$C(t_1,t_2\cdots t_R) = A(t_1,t_2\cdots t_R) B(t_1,t_2\cdots t_R)$$

AのMPS表現

$$A_{t_1t_2\cdots t_R} \approx \sum_{\alpha_1=1}^{D_1} \cdots \sum_{\alpha_{R-1}=1}^{D_{R-1}} M^{(1)}_{t_1,1\alpha_1} \cdots M^{(R)}_{t_R,\alpha_{R-1}1}$$

AをMPOに直す(デルタ関数を各コアにかける）

$$A^{{t'_1t'_2\cdots t'_R}}_{t_1t_2\cdots t_R}\approx \sum_{\alpha_1=1}^{D_1} \cdots \sum_{\alpha_{R-1}=1}^{D_{R-1}} M^{(1)}_{t_1 t'_1,1\alpha_1} \cdots M^{(R)}_{t_Rt'_R,\alpha_{R-1}1}$$

ここで

$$M^{(R)}_{t_jt'_j,\alpha_{j-1}\alpha_{j}} = M^{(R)}_{t_j,\alpha_{j-1}\alpha_{j}} \delta_{t_j, t'_j}$$

図で表現すると

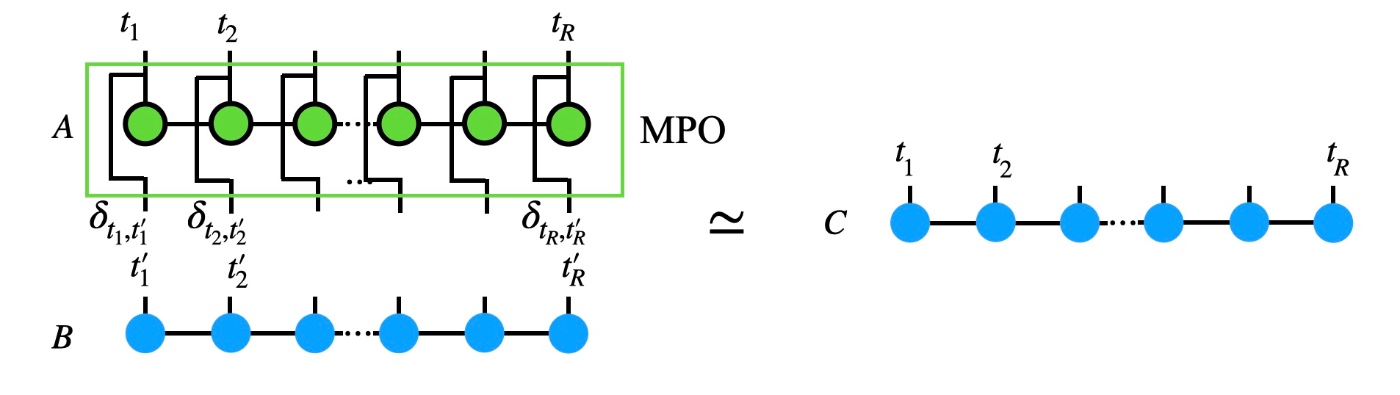
クリノフ部分空間法

例として、全ての要素が2のMPOと全ての要素が1のMPSをそれぞれA,bとする。

この時、$Ax = b$のA,bがMPO,MPSで与えられていて、xをくりのふで求める.

Aを定義

using Quantics

R = 5
sites = siteinds("Qubit", R)
A_mps = 2 .* Quantics.onemps(ComplexF64, sites)
A = MPO(A_mps)

bを定義

b = Quantics.onemps(ComplexF64, sites)
x0 = b

Ax=bを解く.ここでは、ITensorTDVPを用いた。
コードは、こちら

論文は、Time Dependent Variational Principle with Ancillary Krylov Subspace

Time-dependent variational principle with ancillary Krylov subspace

using ITensorTDVP
x = linsolve(A, b, x0; cutoff=1e-30, maxdim=100, nsweeps=10, solver_maxiter=1000, solver_krylovdim=30)

test

_reconst(x) = vec(Array(reduce(*, x), reverse(sites)))
@show maximum(abs, _reconst(apply(A, x)) .- ones(2^R)) # 1.0e-15 
@show _reconst(apply(A, x)) #全て1