こちらの論文:
Learning Feynman Diagrams with Tensor Trains
の和訳になります。
Role of the nesting condition in TCIについての和訳になります。
1. proof of the interpolation property
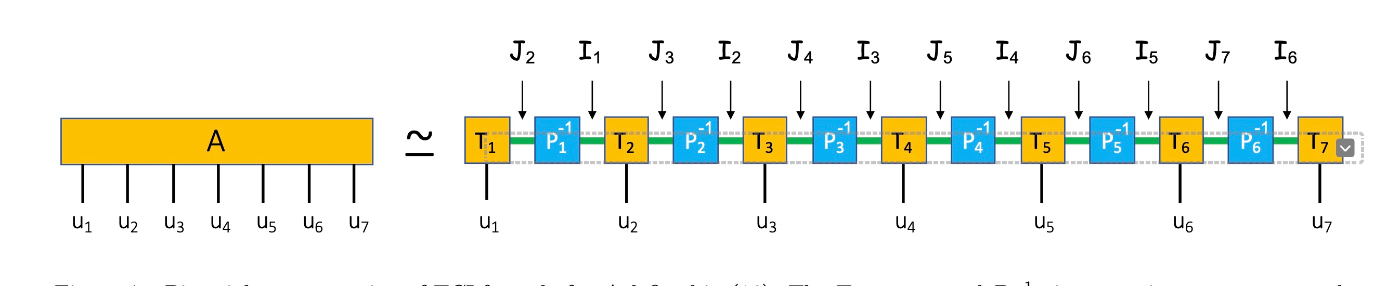
原論文のFigure~4より
(step1)
\begin{equation}
\begin{gathered}
\mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha, \\
\mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-2} \oplus \mathbb{K}_{\alpha-1} \oplus \mathbb{K}_\alpha \\
\mathcal{I}_\alpha \subset \mathcal{I}_0 \oplus \mathbb{K}_1 \oplus \ldots \oplus \mathbb{K}_\alpha .
\end{gathered}
\end{equation}
まず、\mathcal{I}_\alpha の要素は、\mathcal{I}_p (ここで p < \alpha) の要素と、いくつかの u 値が結合されたものとして考えられる。
同様の関係が \mathcal{J} にも適用される。
(step2)
次に、三つのインデックスを持つテンソル T_\alpha は、左と u のインデックスを再グループすることで、行列 T_\alpha^{(L)} として再解釈されます。
この行列のインデックスは、\mathcal{I}_{\alpha-1} \times \mathbb{K}_\alpha および \mathcal{J}_{\alpha+1} です。
この行列は一般的には矩形形状をしていますが、一部の行インデックスは実際には \mathcal{I}_\alpha となります。
同様に、T_\alpha^{(R)} は、u のインデックスと右のインデックスを再グループすることで導入されます。
この行列のインデックスは、\mathcal{I}_{\alpha-1} および \mathbb{K}_\alpha \times \mathcal{J}_{\alpha+1} です。
\begin{aligned}
& T_\alpha^{(L)}\left(\mathcal{I}_\alpha, \mathcal{J}_{\alpha+1}\right) P_\alpha^{-1}\left(\mathcal{J}_{\alpha+1}, \mathcal{I}_\alpha^{\prime}\right)=\delta\left(\mathcal{I}_\alpha, \mathcal{I}_\alpha^{\prime}\right) \\
& P_{\alpha-1}^{-1}\left(\mathcal{J}_\alpha, \mathcal{I}_{\alpha-1}\right) T_\alpha^{(R)}\left(\mathcal{I}_{\alpha-1}, \mathcal{J}_\alpha^{\prime}\right)=\delta\left(\mathcal{J}_\alpha, \mathcal{J}_\alpha^{\prime}\right)
\end{aligned}
\delta\left(\mathcal{I}_\alpha, \mathcal{I}_\alpha^{\prime}\right) と\delta\left(\mathcal{J}_\alpha, \mathcal{J}_\alpha^{\prime}\right) は、単位行列を
与えられた数学的な等式は、行列 T_\alpha^{(L)} と T_\alpha^{(R)} とその他の要素との関係を示しています。特に、これらの行列と P_\alpha や P_{\alpha-1} との関係を示しています。そして、\delta は単位行列を示していると考えられます。
(step3)
元のテンソル A_{\mathrm{TCI}} は、異なるインデックスのセットとテンソル T_\alpha、そして行列 P_\alpha^{-1} の間の積によって近似的に表される。
\begin{aligned}
A_{\mathrm{TCI}}\left(u_1, \ldots, u_n\right) \approx & T_1\left(\mathcal{I}_0, u_1, \mathcal{J}_2\right) P_1^{-1}\left(\mathcal{J}_2, \mathcal{I}_1\right) \\
& \times T_2\left(\mathcal{I}_1, u_2, \mathcal{J}_3\right) P_2^{-1}\left(\mathcal{J}_3, \mathcal{I}_2\right) \\
& \times T_3\left(\mathcal{I}_2, u_3, \mathcal{J}_4\right) P_3^{-1}\left(\mathcal{J}_4, \mathcal{I}_3\right) \ldots
\end{aligned}
ここで、各テンソル T_\alpha は3つのインデックスを持つ:\mathcal{I}_\alpha、u_\alpha そして \mathcal{J}_{\alpha+1}。そして、行列 P_\alpha^{-1} は2つのインデックスを持つ:\mathcal{J}_{\alpha+1} と \mathcal{I}_\alpha。
これらのテンソルと行列の連続した積をとることで、元のテンソルが近似的に再構成される。
(step4)
固定された\alphaの値に対して、TCI形式をピボットインデックスとu_\alphaに対して評価します、(18)式と同様に。
目的はT_\alphaの左右のTとPがキャンセルすることを示すことです。
任意の多重インデックス\left(u_1^*, \ldots, u_{\alpha-1}^*\right) \in \mathcal{I}_{\alpha-1}および\left(u_{\alpha+1}^*, \ldots, u_n^*\right) \in \mathcal{J}_{\alpha+1}に対して、A_{\mathrm{TCI}}は以下のように評価されます:
\begin{aligned}
& A_{\mathrm{TCI}}\left(u_1^*, \ldots, u_{\alpha-1}^*, u_\alpha, u_{\alpha+1}^*, \ldots, u_n^*\right) \\
& =T_1^{(L)}\left(u_1^*, \mathcal{J}_2\right) P_1^{-1}\left(\mathcal{J}_2, \mathcal{I}_1\right) \\
& \times T_2^{(L)}\left(\mathcal{I}_1 \oplus u_2^*, \mathcal{J}_3\right) P_2^{-1}\left(\mathcal{J}_3, \mathcal{I}_2\right) \cdots \\
& T_{\alpha-1}^{(L)}\left(\mathcal{I}_{\alpha-2} \oplus u_{\alpha-1}^*, \mathcal{J}_\alpha\right) P_{\alpha-1}^{-1}\left(\mathcal{J}_\alpha, \mathcal{I}_{\alpha-1}\right) \cdots \\
& T_\alpha\left(\mathcal{I}_{\alpha-1}, \mathbb{K}_\alpha, \mathcal{J}_{\alpha+1}\right) \\
& \times P_\alpha^{-1}\left(\mathcal{J}_{\alpha+1}, \mathcal{I}_\alpha\right) T_{\alpha+1}^{(R)}\left(\mathcal{I}_\alpha, u_{\alpha+1}^* \oplus \mathcal{J}_{\alpha+2}\right) \cdots \\
& P_{n-2}^{-1}\left(\mathcal{J}_{n-1}, \mathcal{I}_{n-2}\right) T_{n-1}^{(R)}\left(\mathcal{I}_{n-2}, u_{n-1}^* \oplus \mathcal{J}_n\right) \\
& \times P_{n-1}^{-1}\left(\mathcal{J}_n, \mathcal{I}_{n-1}\right) T_n^{(R)}\left(\mathcal{I}_{n-1}, u_n^*\right) \\
&
\end{aligned}
最初のラインは、

Discussion