Tensor Cross Interpolationの入門

こちらの論文:
Learning Feynman Diagrams with Tensor Trains
の和訳になります。

:::note warn
物理への応用について現論文を参考にしてください。
:::

tensor cross interpolation (TCI)とは、行列に対するcross interpolation (CI)をテンソルに拡張したものである。

まずTCIの感覚を掴むために、matrix cross interpolation (MCI) についてみていく。

MCI導入

M $\times$ N の行列が与えらたとする。ここで、cross interpolation (CI)を使って、ランク $\chi$の行列で近似することを考えよう。
SVDは、spectral norm(フロべニウスノルム)の意味で、最適なランク $\chi$のAの近似を与えるが、$A$の全ての要素を知らないといけない。
一方のCIは、Aの要素の中から一部分しか探索しないので、SVDに対するadvantageがあるとされる。
この時エラーは最大で、optimal error $\times$ $O(\chi^{2})$である。（optimal error の意味は、おそらくSVDのerrorの意味だと思われるが、詳しくは原論文の引用先を参照。）

記号の定義

$A$の行と列のリストは、それぞれ、

$$\mathcal{I}=\left\{i_1, i_2, \ldots, i_\chi\right\} , \, \mathcal{J}=\left\{j_1, j_2, \ldots, j_\chi\right\}$$

$\mathcal{I}$のa番目の要素を、

$$\mathcal{I}_a \equiv i_a$$

全ての行と列のインデックスのリストは、それぞれ、

$$\mathbb{I}=\{1,2, \ldots, M\}, \, \mathbb{J}=\{1,2, \ldots, N\}$$

行のリスト$\mathcal{I}$と 列のリスト$\mathcal{J}$から構成される$A$の部分行列は、

$$A(\mathcal{I}, \mathcal{J}) , \, A(\mathcal{I},\mathcal{J})_{a b} \equiv A_{\mathcal{I}_a, \mathcal{J}_b}$$

特に、$A(\mathbb{I}, \mathbb{J})=A$ が成り立つ。

MCI

matrix cross interpolationは、以下のように近似を行う(fig2)

$$A=A(\mathbb{I}, \mathbb{J}) \approx A(\mathbb{I}, \mathcal{J}) A(\mathcal{I}, \mathcal{J})^{-1} A(\mathcal{I}, \mathbb{I})$$

この時、2つの性質が成り立つ。

(P1) 内挿公式である。つまり、選んだ行$i \in \mathcal{I}$ もしくは列 $j \in \mathcal{J}$の上で一致する。

(P2) 元々の行列$A$のランクが$\chi$の場合は一致する。

$A(\mathcal{I}, \mathcal{J})$の要素をpivotsと呼ぶ。
また、$A(\mathcal{I}, \mathcal{J})$のことをpivot行列と呼ぶ。

pivotsは、上記の近似において、エラーを最小にするように選ぶべきである。
ピボット行列の組み合わせは、指数関数的に増えてしまうので、それら全てを試して、最小のエラーのになるようなpivotsを選ぶことは不可能である(特にAの次元が大きい場合)。

しかしながら、良いqualityのpivtosをヒューリスティックに選ぶ方法がすでに確立してある。それは、$\textit{maxvol principle}$ (maximum volume)として知られている。

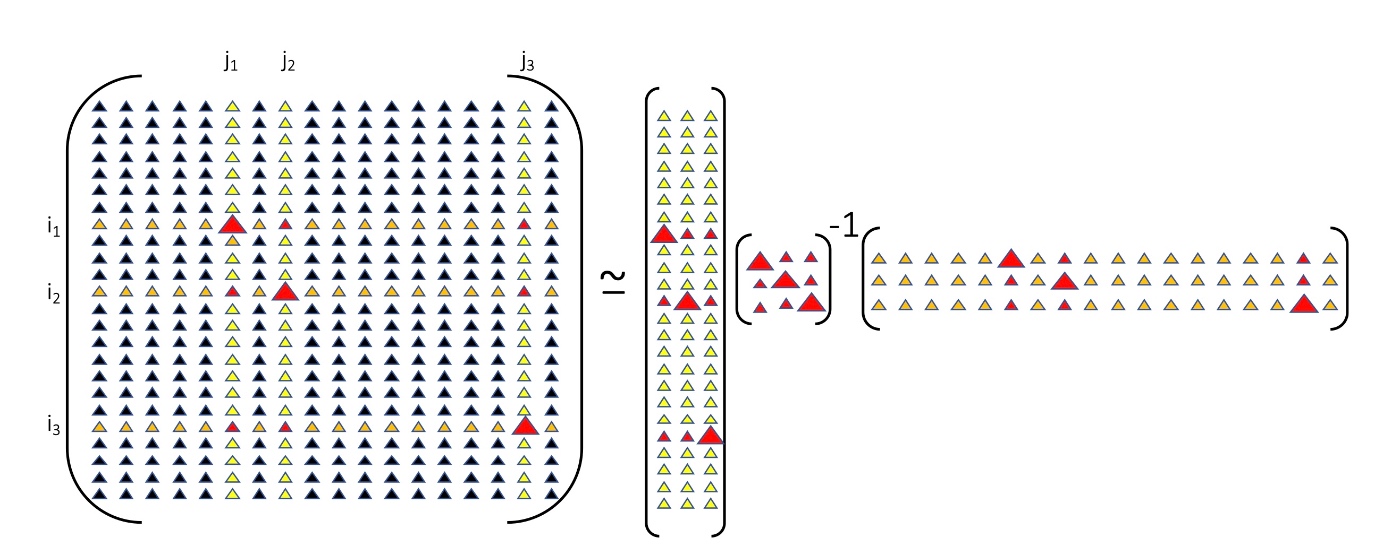
原論文のFigure~2より

TCI導入

TCIとは、MCIを$n$次元のテンソルや(離散化された)多変数関数に拡張したものである。
以下、$n$次元の離散化されたスカラー関数$A(u_1, \cdots, u_n)$を考える。
ここでそれぞれのインデックス$u_i$は、次元$d$の離散化された変数である。この時Aの要素数は、$O(d^{n})$である。
テンソルネットワークの文脈だと、$u_i$は、``テンソルの足''とも呼ばれる。

Naive approach

効率的ではなく実際に使われてないが、教育的な導入をする。

$A$を $A_{\left(u_1\right),\left(u_2, u_3, \ldots, u_n\right)}$のように行列とみなすことができる。
ここで、インデックスを$u_1$と$\textit{multi-index}$ $(u_2, u_3, \ldots, u_n)$のようにグループに分けた。
次に、CIを使って3つの行列の積に分解する(fig3の右側の一番上参照)。
青い行列はピボット行列の逆行列に対応する。
ここで、重要なことは、我々は$\chi$個のpivotsしか保持しないので、repeatedインデックス(図の緑色のインデックス)に対する和は、少数の項しか含まないことである。

次に、fig3の左側の上から２番目のラインを考える。$\chi$個の$u_1$の値と$d$個の$u_2$の値をmulti-index($u_1, u_2$)へグルーピングして、$A_{\left(u_1 ,u_2\right),\left(u_3, u_4\ldots, u_n\right)}$を作る。これにCIを適用する。これをオレンジ色のテンソルが黒色の足を一つしか含まなくなるまで繰り返すことで、tensor trainの形にすることができる(fig3の右側の一番下参照)。

この時、性質の(P2)をテンソルに拡張したものが満たされる(証明は補足C参照）

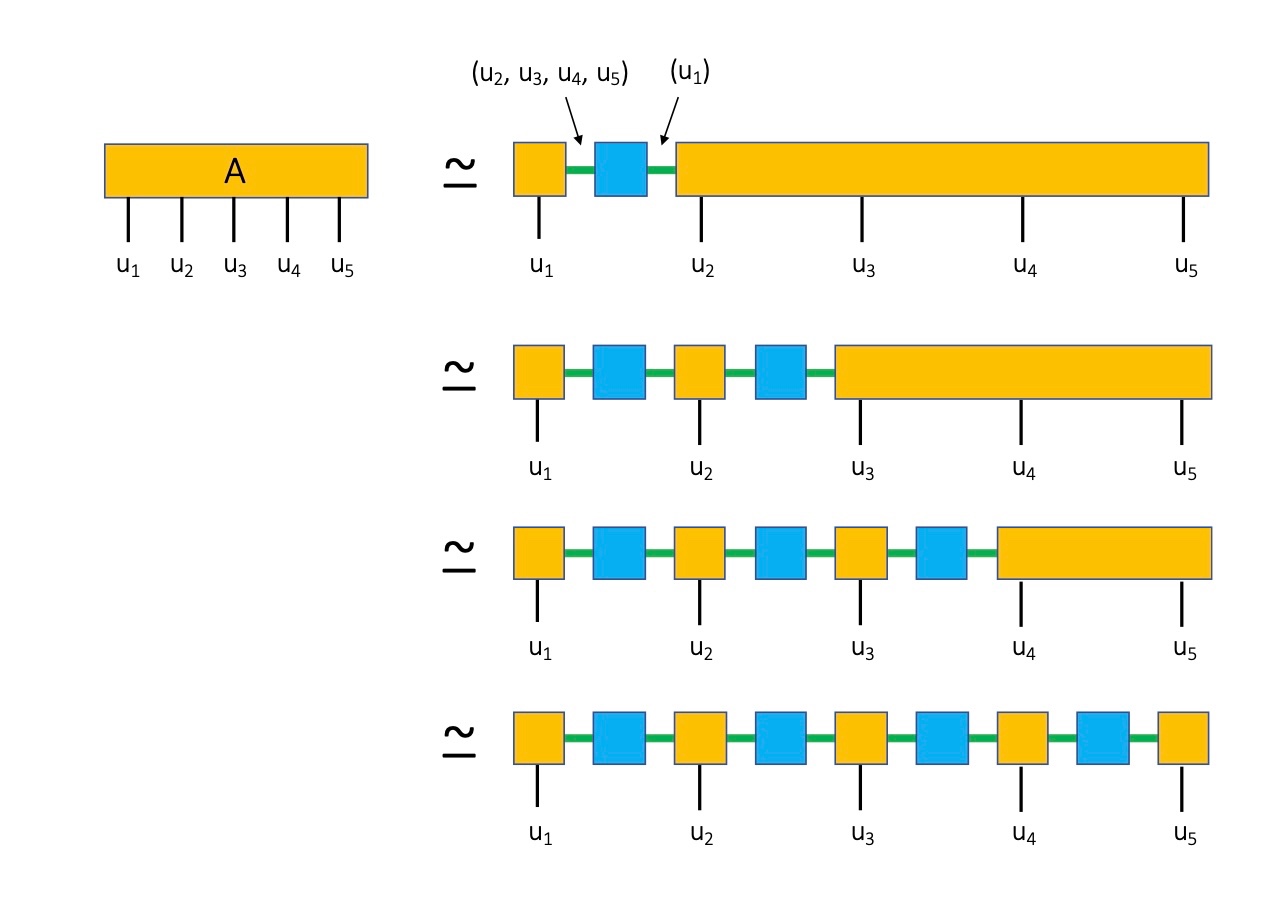
原論文のFigure~3より

tensor train interpolation

TCIのゴールは、関数$A(u_1, \cdots, u_n)$を少数の呼び出し回数で、上記セクションの分解を行うことである。
ここで、TCIの記号と定義を行う。tensor trainのノーテーションはfig4を参照。

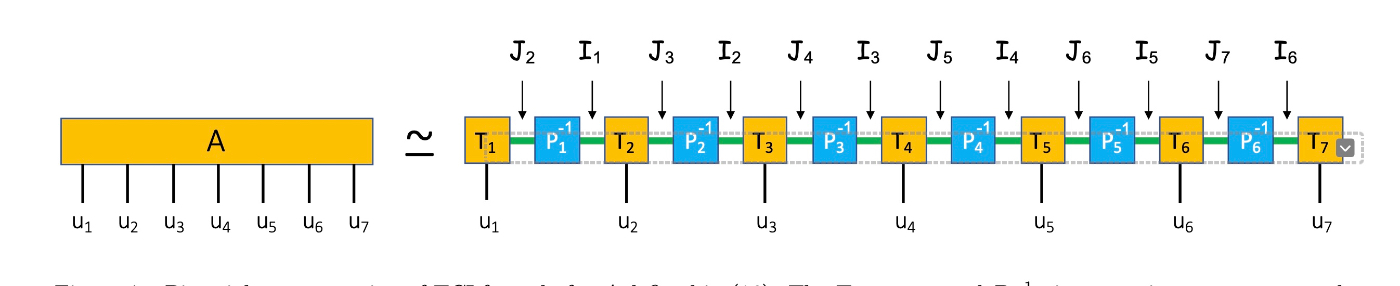
原論文のFigure~4より

関数$A(u_1, \cdots, u_n)$を考える。$u_i$の次元は$d$($d$個の離散的な値をとる)とする。
任意の$\alpha$ ($1 \leq \alpha \leq n$)に対して、以下の形式の$\textit{multi-indices}$を使う。

$$i=\left(u_1, u_2, \ldots, u_\alpha\right) , \, j=\left(u_\alpha, u_{\alpha+1}, \ldots, u_n\right)$$

ここで、$\chi$ 個のセットを考える。それぞれの要素は、サイズ $\alpha$のmulti-indices である。

$$\mathcal{I}_\alpha=\left\{i_1, i_2, \ldots, i_\chi\right\}$$

同様に、サイズ$n-\alpha+1$の$\chi$個の multi-indicesを定義する。

$$\mathcal{J}_\alpha=\left\{j_1, j_2, \ldots, j_\chi\right\}$$

ここで、$\mathcal{I}$ は、各要素は、$u_i$の値が入る、listsのlistであることに注意する。

$\mathcal{I}_0$と$\mathcal{J}_{n+1}$は空のmulti-indexからなるセットであると定義する。
以下では、 $i, j$ をmulti-indicesの記号として用いる。
$i, j$ は、$\alpha$ に依存するが特に強調しない場合は、省略する。

ここで、 $\oplus$ をmulti indicesのconcatenationとして定義する:

$$\left(u_1, u_2, \ldots, u_{\alpha-1}\right) \oplus\left(u_\alpha\right) \oplus\left(u_{\alpha+1}, \ldots, u_n\right) \equiv\left(u_1, \ldots, u_n\right)$$

size 1のmulti index, $u_\alpha$の全要素のセット($1 \leq \alpha \leq n$)を

$$\mathbb{K}_\alpha$$

とし、

$\mathcal{I} \oplus \mathcal{J}$を$\mathcal{I}$ と $\mathcal{J}$の要素の全てのconcatenationsのセットを

$$\mathcal{I} \oplus \mathcal{J} \equiv\{i \oplus j \mid i \in \mathcal{I}, j \in \mathcal{J}\}$$

とする。

$T_\alpha$を定義する。

$$T_\alpha\left(i, u_\alpha, j\right) \equiv A\left(i \oplus\left(u_\alpha\right) \oplus j\right)=A\left(u_1, u_2, \ldots, u_n\right)$$

$i \in \mathcal{I}_{\alpha-1}, j \in \mathcal{J}_{\alpha+1}$
$T_\alpha$は、$1 \leq \alpha \leq n$

$P_\alpha$を定義する。

$$P_\alpha(i, j) \equiv A(i \oplus j)=A\left(u_1, u_2, \ldots, u_n\right),$$

$i \in \mathcal{I}_\alpha, j \in \mathcal{J}_{\alpha+1}$.
$P_\alpha$は $1 \leq \alpha \leq n-1$

より抽象的に書くと、

$$\begin{aligned} & T_\alpha \equiv A\left(\mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha \oplus \mathcal{J}_{\alpha+1}\right), \\ & P_\alpha \equiv A\left(\mathcal{I}_\alpha \oplus \mathcal{J}_{\alpha+1}\right) \end{aligned}$$

Fig.4を参照。

$P_0$, $P_n$は、$1 \times 1$の単位行列である。

固定された$\alpha$に対して、$T_\alpha$は、 $\chi \times d \times \chi$の3階のテンソルである。

$T_1$ と$T_n$の次元は、それぞれ、$1 \times d \times \chi$と$\chi \times d \times 1$である。

$\chi$ 個のmulti-indices $i \in \mathcal{I}$と $\chi$個の multi-indices $j \in \mathcal{J}$の中から一つ選ぶ。
次に、$T_\alpha$は、元々のテンソル$A$ の$u_\alpha$に対する一次元上のスライスを定義する。

$u_\alpha=u$を固定した時のテンソルの値の行列を$T_\alpha(u)$として定義することで、行列$T_\alpha$ の記号を用いる。

$$\begin{aligned} {\left[T_\alpha(u)\right]_{i j} } & \equiv T_\alpha(i, u, j) \\ \left(P_\alpha\right)_{i j} & \equiv P_\alpha(i, j) \end{aligned}$$

AのTCI表現は、

$$\begin{equation} A\left(u_1, \ldots, u_n\right) \approx A_{\mathrm{TCI}}\left(u_1, \ldots, u_n\right) \equiv \prod_{\alpha=1}^n T_\alpha\left(u_\alpha\right) P_\alpha^{-1} \end{equation}$$

図は、fig4参照。
図の緑色は、multi-indicesのあるセット$\mathcal{I}_{\alpha}$（行）,$\mathcal{J}_{\alpha}$（列）に対応する。

TCIは、選ばれた行$\mathcal{I}_{\alpha}$と列$\mathcal{J}_{\alpha}$によって定義されている。そのため、正確な$A$の表現を得るためには、選ばれた$\mathcal{I}_{\alpha}$と$\mathcal{J}_{\alpha}$ ($1 \leq \alpha \leq n$)を最適化する必要がある。

nesting condition

ここで、$\mathcal{I}_\alpha$ と $\mathcal{J}_\alpha$ に対してnesting conditionと呼ばれるある制約を課す。

$\mathcal{I}_\alpha\left(\mathcal{J}_\alpha\right)$
は$\mathcal{I}_{\alpha-1}\left(\mathcal{J}_{\alpha+1}\right)$から構成される。

ただし、最後（最初）の変数は例外であり、 $\mathbb{K}_\alpha$から構成される。

$$\begin{aligned} & \mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha \\ & \mathcal{J}_\alpha \subset \mathbb{K}_\alpha \oplus \mathcal{J}_{\alpha+1} . \end{aligned}$$

言い換えると、もし$i \in \mathcal{I}_\alpha$ならば$u_\alpha \in \mathbb{K}_\alpha$に対して、$i=k \oplus u_\alpha$ を満たすような$k \in \mathcal{I}_{\alpha-1}$ が存在する。

同様に$j \in \mathcal{J}_\alpha$ならば、$u_\alpha \in \mathbb{K}_\alpha$に対して$i=u_\alpha \oplus k$ を満たすような$k \in \mathcal{J}_{\alpha+1}$ が存在する。

Appendixでは、nesting conditionがinterpolation property (P1)の一般化を保証することを証明している。

$1 \leq \alpha \leq n$に対して、

$$A_{\mathrm{TCI}}\left(\mathcal{I}_{\alpha-1}, \mathbb{K}_\alpha, \mathcal{J}_{\alpha+1}\right)=A\left(\mathcal{I}_{\alpha-1}, \mathbb{K}_\alpha, \mathcal{J}_{\alpha+1}\right)$$

$T_\alpha$に対する近似が正確ならば、$P_\alpha$に対する近似も正確である。

$A\left(u_1, u_2, \ldots, u_n\right)$ のTCI近似は、$\alpha, i$, and $j$を固定した時に、$A$の一次元のスライス（部分的な評価）から作られる。
それゆえ、たかだか、$O\left(n d \chi^2\right) \ll d^n$ の要素から近似ができる。

TCIを構築するアルゴリズム

初期ポイント$\left(u_1, \ldots, u_n\right)=$ $\left(u_1, \ldots, u_\alpha\right) \oplus\left(u_{\alpha+1}, \ldots, u_n\right)$からスタートする。

$\mathcal{I}_\alpha$と$\mathcal{J}_\alpha$のそれぞれのセットに対して一つの要素をえらために $n-1$ の異なる分割方法がある。

これによって初期の$\chi=1 \mathrm{TCI}$が得られる。
$A\left(u_1, \ldots, u_n\right)$が１変数の関数の積ならば、この近似は正確である。

ここで、Fig. 5の4つ足テンソルに対応するパイテンソル$\Pi_\alpha$を定義する。

$$\Pi_\alpha \equiv A\left(\mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha \oplus \mathbb{K}_{\alpha+1} \oplus \mathcal{J}_{\alpha+2}\right)$$

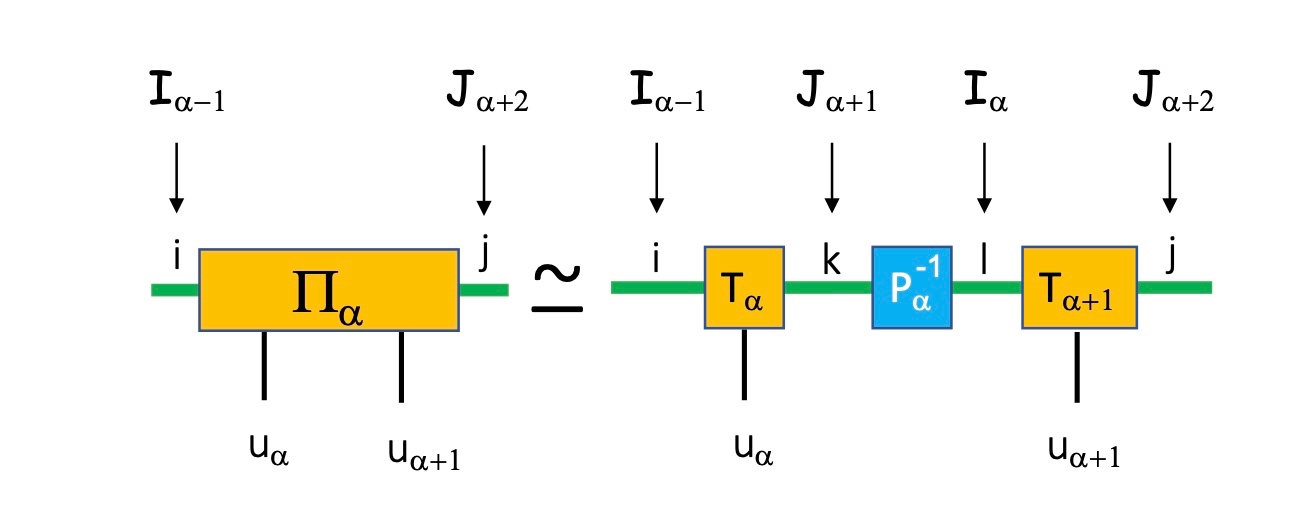
$\Pi_\alpha$を行列とみなすと、$\left(i, u_\alpha\right)$が行のインデックスで、$\left(u_{\alpha+1}, j\right)$ が列のインデックスに対応する。

$\mathcal{I}_\alpha$ と $\mathcal{J}_{\alpha+1}$に対して、$\Pi_\alpha$に対するCI近似をすることができる。
その結果は、$\Pi_\alpha$ は、

$$\begin{array}{r} \Pi_\alpha\left(i, u_\alpha, u_{\alpha+1}, j\right) \approx \sum_{k l} T_\alpha\left(i, u_\alpha, k\right) P_\alpha^{-1}(k, l) \times T_{\alpha+1}\left(l, u_{\alpha+1}, j\right) \end{array}$$

等価な表現として

$$\Pi_\alpha\left(u_\alpha, u_{\alpha+1}\right) \approx T_\alpha\left(u_\alpha\right) P_\alpha^{-1} T_{\alpha+1}\left(u_{\alpha+1}\right) .$$

誤差関数$\epsilon_{\Pi}$を導入する:

$$\begin{equation} \begin{aligned} & \epsilon_{\Pi}\left(i, u_\alpha, u_{\alpha+1}, j\right) \equiv \mid \Pi_\alpha\left(i, u_\alpha, u_{\alpha+1}, j\right)- \\ & \sum_{k l} T_\alpha\left(i, u_\alpha, k\right) P_\alpha^{-1}(k, l) T_{\alpha+1}\left(l, u_{\alpha+1}, j\right) \mid \end{aligned} \end{equation}$$

ここで、$i \in \mathcal{I}_{\alpha-1}, u_\alpha \in \mathbb{K}_\alpha, u_{\alpha+1} \in \mathbb{K}_{\alpha+1}$ と $j \in \mathcal{J}_{\alpha+2}$.

Appendix C 2では、誤差関数が以下を満たすことが示されている。

$$\epsilon_{\Pi}\left(i, u_\alpha, u_{\alpha+1}, j\right)=\left|A-A_{\mathrm{TCI}}\right|\left(i, u_\alpha, u_{\alpha+1}, j\right)$$

言い換えると、$\Pi_\alpha$ の因数分解の誤差は、実際には $i$ と $j$ によって決まる二次元のスライス上で計算される、$A$ に対する補間 $A_{\mathrm{TCI}}$ の誤差である。
したがって、$\Pi_\alpha$ の因数分解を向上させることで、$A$ の全体的なTCI表現も向上する

このアルゴリズムは、$\Pi_\alpha$の近似を向上させるために、ネスティング条件を維持するように、集合$\mathcal{I}_\alpha$と$\mathcal{J}_{\alpha+1}$にさらにピボットを追加する。

アルゴリズムは、誤差関数$\epsilon_{\Pi}$の局所的な最大値$(i, u_\alpha, u_{\alpha+1}, j)$を探す。
$i \in \mathcal{I}_{\alpha-1}$および$j \in \mathcal{J}_{\alpha+2}$の場合、新しいピボット$i \oplus(u_\alpha)$と$(u_{\alpha+1}) \oplus j$をそれぞれ$\mathcal{I}_\alpha$と$\mathcal{J}_{\alpha+1}$に追加し、ピボット行列$P_\alpha$を更新する。

この手順はネスティング条件を保持する。

誤差が最大のピボットを追加する理由は、選んだ点上で正確になるため、TCI近似の精度が最も大きく向上するからである。
付録B2で示されているように、この選択は対応する$P_\alpha$行列の行列式が最大となる、すなわちmax-vol原理に従う。
（先行研究ではピボット行列の行列式を最大化するピボットの選び方、すなわちmaxvol原理が一般的に取られる。一方で、誤差関数$\epsilon_{\Pi}$が最大になるピボットを選ぶ方法もある。実は、この二つの方法は実は非常に類似している。）

$\epsilon_{\Pi}$の最大を探す方法は、2つある。

sweepを行う。

付録A

付録B

付録C

proof of the interpolation property

proof of the

canonical form and the nested condition

(step1)

$$\begin{equation} \begin{gathered} \mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha, \\ \mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-2} \oplus \mathbb{K}_{\alpha-1} \oplus \mathbb{K}_\alpha \\ \mathcal{I}_\alpha \subset \mathcal{I}_0 \oplus \mathbb{K}_1 \oplus \ldots \oplus \mathbb{K}_\alpha . \end{gathered} \end{equation}$$