画像データを行列積分解してみた。
行列積は、テンソルの表現方法の一種です。最近、あるテンソルを行列積の形式で表現する方法を学んだので、練習がてら、適当な画像を行列積の形式で表現して、データを圧縮してみたいと思います。なお、画像の圧縮自体はもっと性能が良い方法があるようです。
画像のインポート
まずは適当な画像を出力します。
import numpy as np
from numpy.linalg import svd, matrix_rank
from PIL import Image
img = Image.open('smile-1.png')
gray_img = img.convert('L')
gray_img.save('smile_mono.png')
a = np.asarray(gray_img)

ここでは上記の256*256行列を行列の積の形で分解し、特異値分解して、低ランク近似を行います。
厳密に行列積の形で表現する
ここでは、以下のように8つの行列積の形で表現してみます。全然行列のように見えないですが、下にある足の添字を固定して、横に伸びているテンソルの足を1本だとみなすと、行列が横一列に並んでいると
見なすことができます。

行列積は、例えば左から順番に特異値分解を繰り返すことで小さい行列を左から作っていきます。
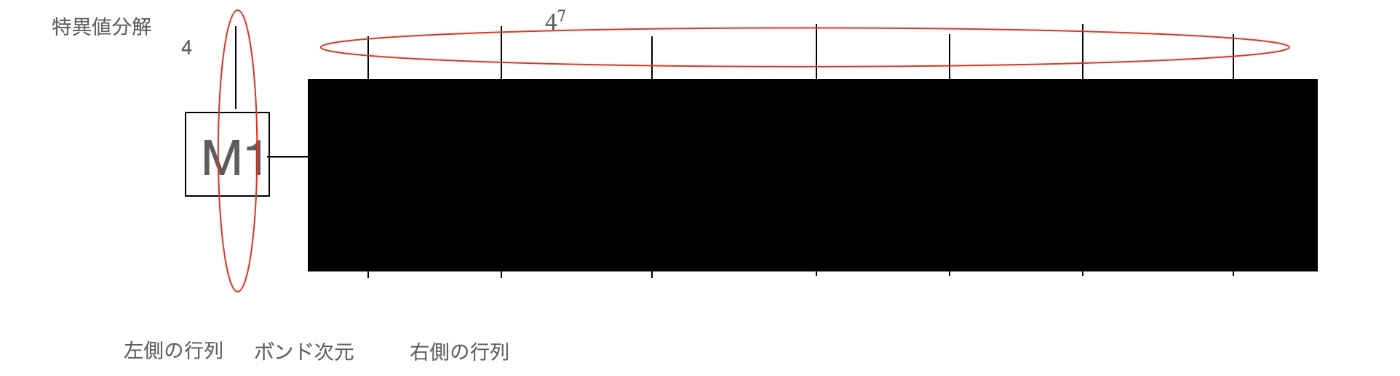
作り方の最初のステップを以下の図に示します。ここでは、特異値分解をすることで、左側に小さい行列(4×4行列)と右側に大きい行列(4^7✖×4^7行列)に分けています。この手順を大きい行列に対して行います。この操作を繰り返すことで行列が横一列に並んだ上のような表現(行列積)ができます。本記事では、この操作をpythonのreshapeを使って、数値的に実装したものになります。
上の行列積の図より、これらの右と左行列の間を繋ぐ次元は真ん中で最大となり、以降、両側の端に近づくにつれて小さい値を取ることがわかります。この性質は、特異値分解をする際に、ボンド次元は、左右の行列の小さい方の次元を採用する、と言うところからわかります。
いかにコードを示します。こちらの資料(https://github.com/utokyo-qsw/joint-seminar)
を参照して作らせていただきました。
#8つのテンソルに分解し、テンソルの添字を0から順に並び替える。
a_tensor = a.reshape(4,4,4,4,4,4,4,4)
a_tensor = a_tensor.transpose(0,1,2,3,4,5,6,7).reshape(4,4,4,4,4,4,4,4)
行列積に分解。
a_tensor.reshape(4,4**7)
u1, s1, vh1 = svd(a_tensor.reshape(4, 4**7),full_matrices=False)
M1 = u1
u2, s2, vh2 = svd((np.diag(s1) @ vh1).reshape(4**2, 4**6),full_matrices=False)
M2 = u2.reshape(4,4,4**2)
u3, s3, vh3 = svd((np.diag(s2) @ vh2).reshape(4**3, 4**5),full_matrices=False)
M3 = u3.reshape(4**2,4,4**3)
u4, s4, vh4 = svd((np.diag(s3) @ vh3).reshape(4**4, 4**4), full_matrices=False)
M4 = u4.reshape(4**3,4,4**4)
u5, s5, vh5 = svd((np.diag(s4) @ vh4).reshape(4**5, 4**3),full_matrices=False)
M5 = u5.reshape(4**4,4,4**3)
u6, s6, vh6 = svd((np.diag(s5) @ vh5).reshape(4**4, 4**2),full_matrices=False)
M6 = u6.reshape(4**3,4,4**2)
u7, s7, vh7 = svd((np.diag(s6) @ vh6).reshape(4**3, 4),full_matrices=False)
M7 = u7.reshape(4**2,4,4)
M8 = np.diag(s7) @ vh7
def reconstruct_matrix(M1,M2,M3,M4,M5,M6,M7,M8):
matrix = np.einsum("ab,bcd,def,fgh,hij,jkl,lmn,no -> acegikmo",M1,M2,M3,M4,M5,M6,M7,M8,optimize=True).reshape(4,4,4,4,4,4,4,4).transpose(0,1,2,3,4,5,6,7).reshape(256,256)
return matrix
W_h_reconstructed = reconstruct_matrix(M1,M2,M3,M4,M5,M6,M7,M8)
img3 = Image.fromarray(np.uint8(W_h_reconstructed))
img3.save('smile_mono_MPS_8site.jpg')

以上までは、一切近似は行なっていないので、元の画像が完全に再現できている。
画像データを圧縮
ここで行列積の横方向の次元(これは、ボンド次元と呼ばれる)を圧縮する事によるある種の近似します。ボンド次元(行列の左右の足の次元)を最大でも16になるような制限を加えることで上記の近似を行います。うまくいけば、データが圧縮され、ベクトルと行列の演算が高速になるなどのメリットがあります。
chi_max = 16
## M1 と M2をつなぐボンド
chi_12 = min(chi_max,M1.shape[1])
## M2 と M3をつなぐボンド
chi_23 = min(chi_max,M2.shape[2])
## M3 と M4をつなぐボンド
chi_34 = min(chi_max,M3.shape[2])
## M4 と M5をつなぐボンド
chi_45 = min(chi_max,M4.shape[2])
## M5 と M6をつなぐボンド
chi_56 = min(chi_max,M5.shape[2])
## M6 と M7をつなぐボンド
chi_67 = min(chi_max,M6.shape[2])
## M7 と M8をつなぐボンド
chi_78 = min(chi_max,M7.shape[2])
M1_ap = M1[:,:chi_12]
M2_ap = M2[:chi_12,:,:chi_23]
M3_ap = M3[:chi_23,:,:chi_34]
M4_ap = M4[:chi_34,:,:chi_45]
M5_ap = M5[:chi_45,:,:chi_56]
M6_ap = M6[:chi_56,:,:chi_67]
M7_ap = M7[:chi_67,:,:chi_78]
M8_ap = M8[:chi_78,:]
W_h_ap = reconstruct_matrix(M1_ap,M2_ap,M3_ap,M4_ap,M5_ap,M6_ap,M7_ap,M8_ap)
np.linalg.norm(W_h_reconstructed - W_h_ap)/np.linalg.norm(W_h_reconstructed )
# 0.054004230487981635
img4 = Image.fromarray(np.uint8(W_h_ap))
img4.save('smile_mono_MPS_8site_approx_.jpg')

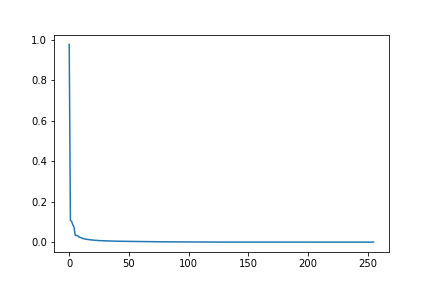
ボンド次元が最大となる中央での特異値のヒストグラムを表示させてみたところ、この画像に関しては以下のような減衰傾向が見られた。
norm_e = s4**2
# 規格化した特異値
x = s4/np.sqrt(norm_e.sum())
import matplotlib.pyplot as plt
plt.plot(x)
plt.savefig("s")
まとめ
行列積分解を画像データに適用してみました。特異値分解との比較や、テンソルの足をランダムに並べ替えたときとの精度の比較、他の画像にも適用してみるなど面白そう。
参考
tensorlyを使えば、簡単にMPS表現を作れるようです。
Discussion