こちらの論文:
Learning Feynman Diagrams with Tensor Trains
の和訳の補足になります
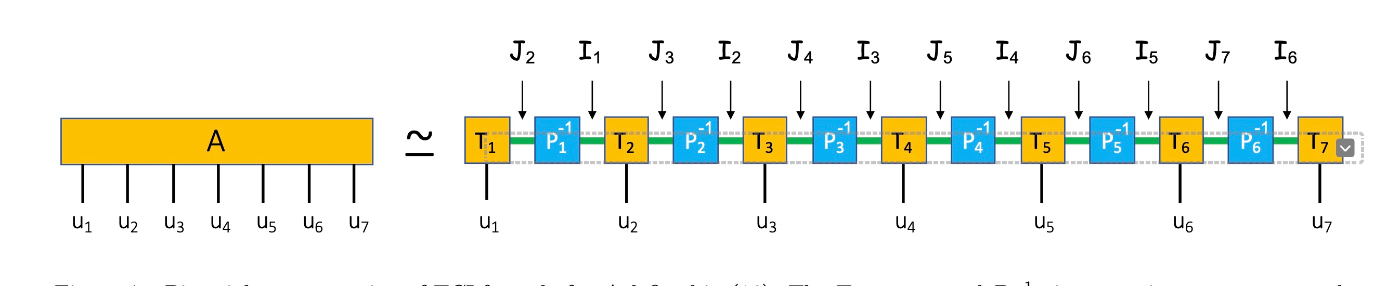
原論文のFigure~4より
u_iの次元はd=2とする(local dims)
ボンド次元は2とする(Iset, Jsetの次元)
テンソルの数は、7である。
nesting condition
ここで、\mathcal{I}_\alpha と \mathcal{J}_\alpha に対してnesting conditionと呼ばれるある制約を課す。
\mathcal{I}_\alpha\left(\mathcal{J}_\alpha\right)は\mathcal{I}_{\alpha-1}\left(\mathcal{J}_{\alpha+1}\right)から構成される。
ただし、最後(最初)の変数は例外であり、 \mathbb{K}_\alphaから構成される。
\begin{aligned}
& \mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha \\
& \mathcal{J}_\alpha \subset \mathbb{K}_\alpha \oplus \mathcal{J}_{\alpha+1} .
\end{aligned}
言い換えると、もしi \in \mathcal{I}_\alphaならばu_\alpha \in \mathbb{K}_\alphaに対して、i=k \oplus u_\alpha を満たすようなk \in \mathcal{I}_{\alpha-1} が存在する。
同様にj \in \mathcal{J}_\alphaならば、u_\alpha \in \mathbb{K}_\alphaに対してi=u_\alpha \oplus k を満たすようなk \in \mathcal{J}_{\alpha+1} が存在する。
具体例
fully nested
\mathcal{I}セットから見ていく。
\mathcal{I}_1 = [[0], [1]]
\mathcal{I}_2は、\mathcal{I}_1から構成される。ここで、\mathcal{I}_1 \oplus u_2は、[[0,0], [1,0], [0,1], [1,1]]となる。
このセットから、2つ選ぶので(ボンド次元2)、\mathcal{I}_2は、例えば
\mathcal{I}_2 = [ [0,0], [1,0] ]
以下、同様である。
\mathcal{I}_3は、\mathcal{I}_2から構成される。ここで、\mathcal{I}_2 \oplus u_3は、[[0,0,0], [1,0,0], [0,0,1], [1,0,1]]
このセットから、2つ選ぶので(ボンド次元2)、\mathcal{I}_3は、例えば
\mathcal{I}_3 =
[[0,0,0], [1,0,0]]
このような操作を繰り返していくと、最終的に
\mathcal{I}_6 =
[[0,0,0,0,0,0], [1,0,0,0,0,0]]
のような感じで得られる。
この次元は、ボンド次元に対応する。
それぞれの要素には、u_1からu_6のスカラー値の集合が入る。
次元は、テンソルの数よりも1つだけ少ない。
結果として、
\begin{equation}
\begin{gathered}
\mathcal{I}_6 \in \mathcal{I}_5 \oplus \mathbb{K}_6,\\
\cdots , \, \\
\mathcal{I}_3 \in \mathcal{I}_2 \oplus \mathbb{K}_3 , \\
\mathcal{I}_2 \in \mathcal{I}_1 \oplus \mathbb{K}_2 , \\
\mathcal{I}_1 \in \mathcal{I}_0 \oplus \mathbb{K}_1
\end{gathered}
\end{equation}
このような関係を\mathcal{I}について、fully nestedという。
つまり、i \in \mathcal{I}_\alphaとu_\alpha \in \mathbb{K}_\alphaに対して、i=k \oplus u_\alpha を満たすようなk \in \mathcal{I}_{\alpha-1} が存在する。
平たくいうと、\mathcal{I}_1の選び方に、それ以降の\mathcal{I}セットは引っ張られるということになる。
別の表現では
\begin{equation}
\begin{gathered}
\mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha, \\
\mathcal{I}_\alpha \subset \mathcal{I}_{\alpha-2} \oplus \mathbb{K}_{\alpha-1} \oplus \mathbb{K}_\alpha \\
\mathcal{I}_\alpha \subset \mathcal{I}_0 \oplus \mathbb{K}_1 \oplus \ldots \oplus \mathbb{K}_\alpha .
\end{gathered}
\end{equation}
と書くこともできる。
\mathcal{J}セットについても見ていく。
\mathcal{J}_7 = [[0],[1]]
\mathcal{J}_6は、\mathcal{J}_7から構成される。ここで、\mathcal{J}_7 \oplus u_6は、[[0,0], [1,0], [0,1], [1,1]]となる。
このセットから、2つ選ぶので(ボンド次元2)、\mathcal{J}_6は、例えば
\mathcal{J}_6 = [[1, 0],[1,1]]
以下同様である。
このような操作を繰り返していくと、最終的に
\mathcal{J}_2 =
[[1,0,0,0,0,0], [1,1,0,0,0,0]]
のような感じで得られる。
この次元は、ボンド次元に対応する。
それぞれの要素には、u_2からu_7のスカラー値の集合が入る。
次元は、テンソルの数よりも1つだけ少ない。
結果として、
\begin{equation}
\begin{gathered}
\mathcal{J}_2 \in \mathbb{K}_{2} \oplus \mathcal{J}_3 , \\
\cdots , \, \\
\mathcal{J}_5 \in \mathbb{K}_{5} \oplus \mathcal{J}_6 , \, \\
\mathcal{J}_6 \in \mathbb{K}_{6} \oplus\mathcal{J}_7 , \, \\
\mathcal{J}_7 \in \mathbb{K}_{7} \oplus\mathcal{J}_8 , \, \\
\end{gathered}
\end{equation}
このような関係をJについて、fully nestedという。
j \in \mathcal{J}_\alphaならば、u_\alpha \in \mathbb{K}_\alphaに対してi=u_\alpha \oplus k を満たすようなk \in \mathcal{J}_{\alpha+1} が存在する。
補足
fig4参照の描くテンソルを抽象的に描くと、
\begin{aligned}
& T_\alpha \equiv A\left(\mathcal{I}_{\alpha-1} \oplus \mathbb{K}_\alpha \oplus \mathcal{J}_{\alpha+1}\right), \\
& P_\alpha \equiv A\left(\mathcal{I}_\alpha \oplus \mathcal{J}_{\alpha+1}\right)
\end{aligned}
T_\alpha は、\mathbb{K}_\alphaの中の要素u_\alphaに対して、一次元配列が定義でき、その配列に対する関数である。
具体的に、\alpha=2を考える。
\begin{aligned}
& T_2 \equiv A\left(\mathcal{I}_{1} \oplus \mathbb{K}_2 \oplus \mathcal{J}_{3}\right), \\
& P_2 \equiv A\left(\mathcal{I}_2 \oplus \mathcal{J}_{3}\right)
\end{aligned}
T_2 は、\mathbb{K}_2の中の要素u_2に対して、一次元配列が定義できる。
その配列は、例えば、u_2=1ならば、
T_2 = [[0], [1]] \oplus [1] \oplus [[1,0,0,0,0], [1,1,0,0,0]]
各配列の次元は7となる。これは、テンソルの数とも一致している。
P_\alphaも同様に考える。
まとめ
左から右にsweepする時は、Isetを更新することで、自動的にnested conditionが満たされる。
右から左にsweepするときは、Jsetを更新することで、自動的にnested conditionが満たされる。
nested condtionのありがたみについては、別記事にて。

Discussion