連続時間拡散モデルとRectified Flowに関する考察
以下に示す内容は専門に研究しているわけでもない学生の戯言程度に思ってほしいという保険の文章を最初に投稿しておく.
SDEによる定式化とODE
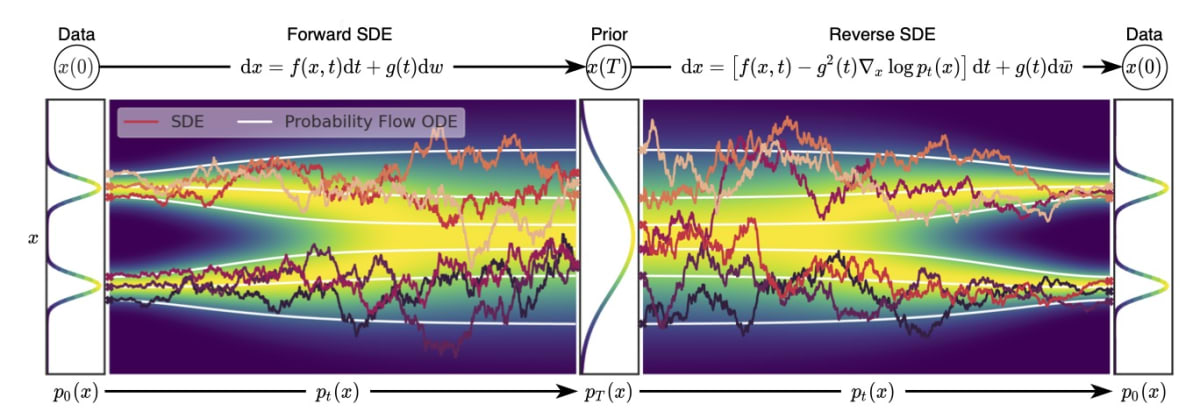
連続時間における生成モデルというのは,SongらのScore-SDEのように,SDEによる定式化が可能である.
つまり,データ分布からあるガウシアンへの輸送を考える際に,その軌道はガウシアンノイズによってブラウン運動のような軌道になる.
よく用いられる図に以下のような物がある.
このように,軌道にランダム性がある.
しかし,このランダム性は本当にいるのだろうか?
つまり,直線による軌道を考えればもっと簡単にならないだろうか?
誤解を恐れず言えばSDEからランダム性をなくす,つまりSDEの第2項のdiffusionの項をなくしたODEを考える.
Score-SDEの論文では,backward processにおいて,対応するSDEと同じ分布に従うODE(Probability Flow ODE)が提案されている.
では,forward processもODEとして定式化するとどうなるだろうか?
実際には、Score-SDEのODEを使えば良いと考えられるが、もっと簡単に直線軌道を扱う方法はあるだろうか?
そのような疑問をいだいた際に以下に示す論文を見つけた.
これらの論文は拡散モデルというより,Flowらしい。
(2つ目の論文のsecond authorにNeural ODEの著者がいて,懐かしさを感じた.
いずれもある分布からある分布への輸送をFlowの文脈で考えるものである.
中でも一番簡単な1つ目のものと3つ目のものの中のSimplified Versionを考える.
1つ目のものは に大雑把な解説を書いた,
改めて示すと,2つの分布のサンプルを
ベクトルで考えれば,その方向ベクトルは
また,その間の状態
これをODEで表せば,
で表せる.
推論時には元の分布のサンプル
つまり,
すると,上のODEは
で表せる.
推論時にはODEソルバーで解けば良い.
本当に直線軌道になるのならオイラー法で1ステップ推論が可能であるが,そうとは限らない.
3つ目の論文では,この定式化の軌道にガウシアンノイズを加えたようなものを考えており,また,各バッチにおける最適輸送,シュレディンガーブリッジを考えて性能向上を図っている.
つまり,ミニバッチごとのガウシアンと画像に対して最適輸送を考えて,できるだけ近い距離のペアを見つけるといったものである.
シュレディンガーブリッジについては自分の理解が乏しいため割愛する.
以上のように,ODEでの定式化を示した.
上の記事では実験を行っており,128x128のAFHQのcatの生成を行っている.
(記事には載せていないが)score-sdeでの実験結果と比べると,パット見の主観評価は匹敵する程になっている.
| score-sde | rect_flow |
|---|---|
 |
 |
 |
 |
 |
 |
疑問と実験
ここで,疑問に思ったのが,輸送元の分布についてである.
上の実験では,ガウシアンからの輸送を考えた.つまり、生成時にも同じ分布からサンプリングし、生成を行う.
つまり,割と推論しやすい軌道になっていると考えられる.
そこで,自分が今までやっていた音声合成で実験を行った.
目的としては,元の分布はガウシアンであることに変わりないが,その平均と分散にニューラルネットワークの出力を用いる場合にもこの手法は有効であるか検証するためである.
実際にGrad-TTSと呼ばれる音声合成モデルで実験を行った.
モデルの構造としては,入力として音素,出力がメルスペクトログラムの音響モデルで,
音素 => Encoder(Transformer) => 音素レベル to フレームレベル => Decoder(Diffusion) => メルスペクトログラム
という流れの変換を行う.
Grad-TTSとScore-SDEの違いは,Score-SDEでは
ただし,論文では
また,平均
実験として,論文の再現と上のODEによる方法を比較する.
Grad-TTSの著者実装では,オイラー法による推論でbackward processを実装しているが,本実験ではどちらもscipyのODEソルバー(RK45)を使用する.
なお,実験条件は以下の通りである.
- data : JSUT
- 100epoch
実験結果として,オープンデータの生成メルスペクトログラムを示す.
| Grad-TTS | ODE |
|---|---|
 |
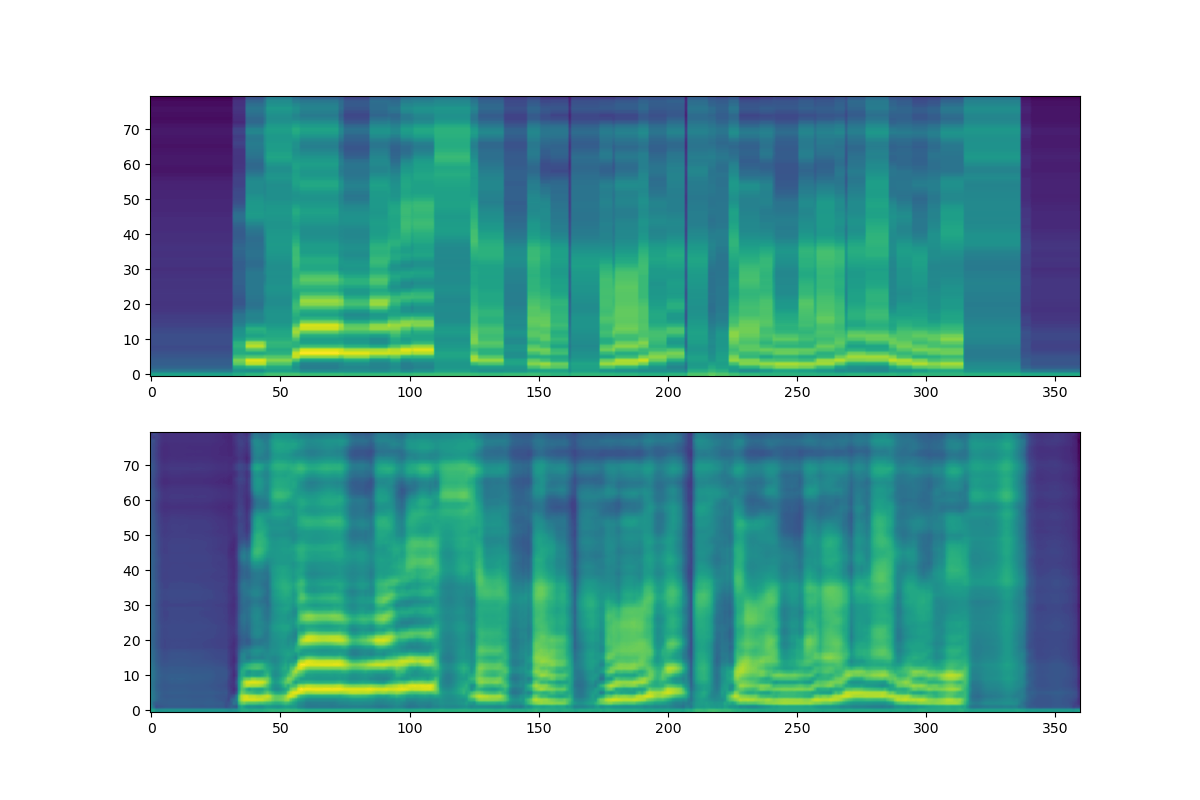 |
各画像の上のプロットが平均メルスペクトログラム(Encoderの出力をexpandしたもの)で,下が生成結果(Decoderの出力)である.
結果として,ODEによる定式化では明らかに平滑化した出力が得られており,またメルスペクトログラムの縞が十分に生成できていないのに対し,Grad-TTSの出力は縞も問題なく,高周波成分も生成できていることがわかる.
どちらの実験でも輸送元の分布はガウシアンであるが,メルスペクトログラムに関する分布の平均は空間において音声ごとに異なる位置にある一方で,画像の実験の分布は
そのため,ODEで考えているような直線軌道では未知データに対する軌道が学習でカバーしきれておらず,上のような結果になったのではないかと考えている.
一方で,SDEによる定式化では,ノイズによるランダム軌道により,未知データに対する軌道もカバーできるように学習できているのではないかと考えた.
(画像のときは元の分布が生成時にも
では,ODEの軌道にランダム性を入れればよいのだろうか?
ここで,画像のときに示したConditional Flow Matchingのように,軌道にノイズを入れる.
すると,以下のような結果が得られた.
| ODE | ODE with noise |
|---|---|
 |
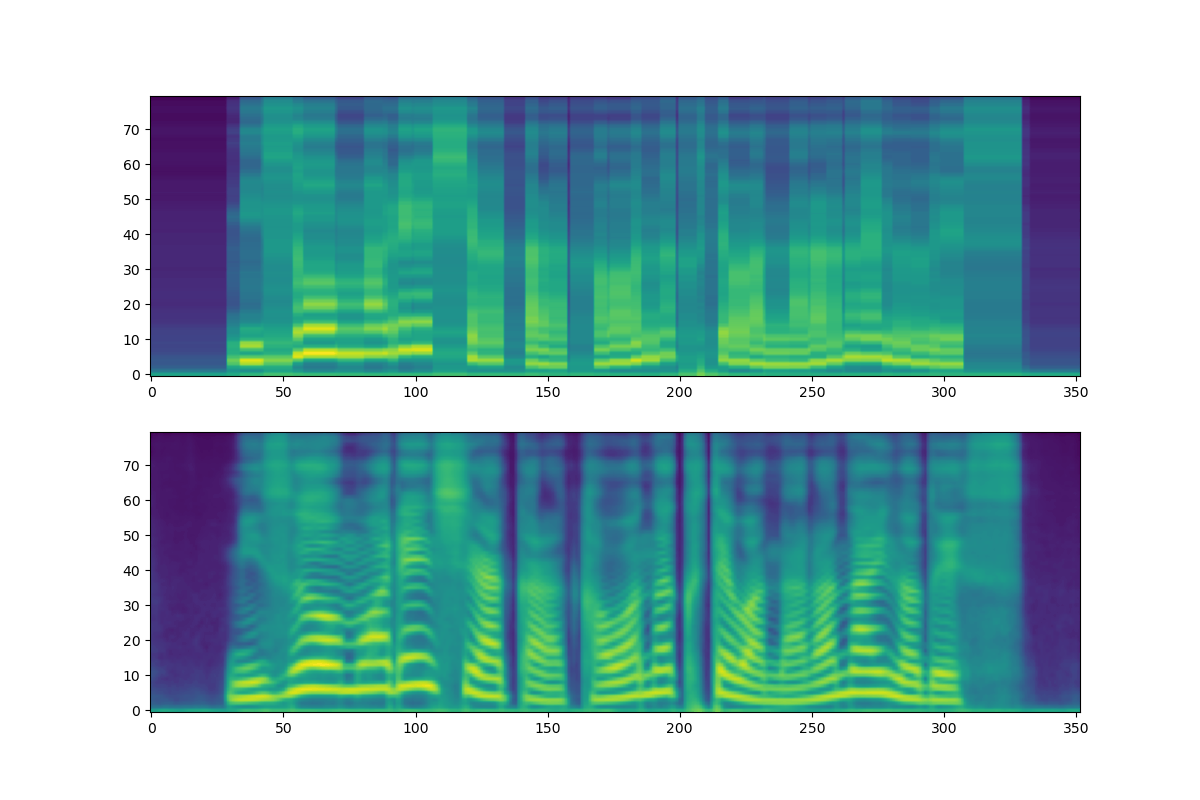 |
Grad-TTSに比べると,平滑化しているが,縞が現れておりマシな結果になっている.
このように,ノイズはそのランダム性によって,未知データに対する軌道の学習を促進させているだけでなく,高周波成分の学習の助けもしていると考えられる.
Scoreベースの手法(特にSMLD)のときからこの問題はあるため,すごく自明なことを書いた気がするが,ノイズの効果を実験で確認できてよかったように思う.
Grad-TTS
ODE-TTS