「懲罰マッチ」発生の仕組みをシミュレーションで検証する
はじめに
みなさんは複数人チーム同士でのオンライン対戦ゲームにおいて、「懲罰マッチ」「介護マッチ」と呼ばれる現象を耳にしたことはあるでしょうか?
これは、試合のたびに固定メンバーではない、いわゆる「野良」メンバー複数人でチームを組み、同じく野良メンバーで構成された相手チームと戦うタイプのオンラインゲームにおいて、半ば都市伝説のごとく囁かれている噂です。
曰く、「連勝した後は必ず弱い味方と組まされる」「連勝したあと必ず連敗する、運営に勝率が5割になるように調整されている」と。

筆者も4vs4や5vs5形式のオンライン対戦ゲームをしばしばプレイすることがありますが、確かに「これは懲罰マッチ入った...」と思ってしまうような事象を目にすることがあります。
これは果たして本当にただの都市伝説で負けが込んだプレイヤーの幻想なのでしょうか?
ゲーム開発者・運営サイドには懲罰マッチを組ませてでも全体の勝率が5割に収束するように調整するメリットは特に無いと思われるので、なにか別の要因で発生している可能性もあります。
この発生メカニズムが氣になって夜しか寝られない日々が続いたので、シミュレーションを行い検証してみようと思います。
予想
もしチーム編成がその時間試合に申し込んだプレイヤー内で完全にランダムに行われる方式なのだとしたら、懲罰マッチは完全に気の所為と言えるでしょう。
仮に「自分より弱い味方ばかりチームに来る」という現象が発生したとしても、それはあなたのレートが平均より高いから発生しやすいというだけということになります。
しかし現実のレーティングやランクが導入されたオンライン対戦ゲームでは、試合が一方的になりすぎずに万人が楽しめるように、 実力が近いもの同士で試合が組まれるようになっています。このマッチングの影響でチーム編成に偏りが発生(つまり懲罰マッチが発生)している可能性があります。
マッチングの条件をいくつかのパターンでシミュレーションを行うことで確かめることができないかと考えています。
レーティングとランク
レーティング
対戦ゲームにおいて、プレイヤーの強さを表す数値としてレーティングが導入されることが多いです。
プレイヤー同士の対戦結果に基づき、レーティングの値が変動し、レーティングが高いプレイヤーほど強いとされる指標です。
代表的なレーティングのアルゴリズムとして、イロレーティングが知られています。
イロレーティングではプレイヤーの初期レート・平均レートを1500とし、連続値で(小数点第n位で切られることは多いが)表されます。
例えば、レーティング差による勝率は次のように表されます。
| レーティング差 | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
|---|---|---|---|---|---|---|---|---|---|
| 上位者勝利確率 | 50% | 57% | 64% | 70% | 76% | 81% | 85% | 88% | 91% |
| 下位者勝利確率 | 50% | 43% | 36% | 30% | 24% | 19% | 15% | 12% | 9% |
ランク
また、レーティングではなくランク制度を導入している対戦ゲームも多くあります。他にも「段位」や「ウデマエ」などゲームに応じて呼称は様々ですが、総じてプレイヤーの強さを数段階の離散値で表す目的で使用されるものを指します。
算出方法は多岐に渡りますが、シンプルなものだと勝利数と敗北数から決まるようなものもあります。
勝利するとポイントが1増え、敗北するとポイントが1減り、5ポイント貯めることで1つ上のランクへ移行というようなシステムです。

勝ち星によるランク上昇の例
他にも勝敗だけでなくゲーム中の行動を評価してポイントを増減させる仕組みとし、長期間ゲームをプレイすることで自然とランクが上がる設計にしているゲームも多いかと思います。
対象とするゲームシステム
今回は以下のような対戦ゲームを想定します。
おそらく5vs5等でも結果に大きな差は現れないと思います。
- 4人 vs 4人の形式で1試合が行われるゲーム
- チーム編成は野良のみとする
- 試合では必ず勝敗が決まる
- レーティングシステムが搭載されている
- 試合開始時に味方の強さ順がわかるものとする
「懲罰マッチ」の定義
懲罰マッチに関する情報を集めるに、主に以下のような状況でプレイヤーは懲罰マッチだと感じるようです。
- 連勝後など調子が良い状況が続いた後に発生する
- 連続で負ける
- (レートやランク的に)格下の味方と組まされる(結果、負ける)
試合開始時に味方のレートやランク、または味方内でのこれらの序列が表示されるゲームは珍しくありません。(例: 試合開始前のメンバー一覧がランクの降順で表示される)
これらの順序だったり、試合中の実際の味方の様子だったりから「弱い味方と組まされた」と思ってしまうのだと想定できます。
また、これら味方の強さの情報がまったく得られないゲームであっても、結果を振り返ると「5連勝後に5連敗した。きっと後半は懲罰マッチを組まされた」と感想を抱くこともあるでしょう。
以上はあくまで人間の主観的な評価なので、シミュレーションを行うにあたり、どういった状況になったら懲罰マッチなのかを定義しないといけません。
今回は仮に2パターンの状況を懲罰マッチと定義します。
懲罰マッチ 定義A
N連勝後、N連敗した
確率は収束するとは言いますが、じゃんけんで10連勝した後は負けやすくなるといったことはありません。したがって、連勝後に連敗することが通常の確率より多く発生した場合はチーム編成による影響だった可能性があると言えるでしょう。
懲罰マッチ 定義B
N連勝後、自分よりレートが低い味方のみで構成されるチームでの試合がN回続いた
※Nの値はシミュレーション時にいくつか変化させて検証します。
主にTwitter上で多く観測できる意見がベースになっています。
シミュレーション
シミュレーションをいくつかの条件で行っていきます。
基本的に以下の条件はシミュレーションごとに同じとしています。
- プレイヤー数: 256名
- 初期レート: 1500
- 試合数: 各人100回
- イロレーティングの係数: 32
- 100回シミュレーションを行い、結果の平均値を算出
シミュレーション結果は以下の表の形式で掲載します。
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 25.0 | 6.0 | 2.0 |
| 定義B | 87.0 | 48.0 | 30.0 |
定義A = N連勝後にN連敗 なので、5連勝後に5連敗という事象が25回観測されたことになります。
プレイヤーは256名なので、10%程度のユーザーが100試合を行ううちに一度体験する程度となります。
レーティング
レーティングの計算にはイロレーティングを利用します。
本来このアルゴリズムは1vs1のゲーム専用ですが、レートの更新計算時に相手チームの平均レートを利用することで多人数vs多人数のゲームに応用する方法が知られており、これを利用します。
1.完全ランダムマッチ + 勝敗ランダム
まずはチーム編成が完全ランダムの場合の懲罰マッチの発生数を確認しておきます。
勝敗も完全ランダム(1/2で勝ち)とします。
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 23.09 | 5.79 | 1.47 |
| 定義B | 93.8 | 50.1 | 26.98 |
完全にランダムでマッチングと勝敗が決まるため、定義Aの連勝後に連敗する確率は低くなっていきます。
また、勝利すれば自分のレートが高くなるため、その後のマッチングで自分の味方が自分以下のレートである確率も上がっていきます。そのため定義Bは定義Aよりも発生しやすいと言えます。
2. 完全ランダムマッチ + 完全実力制
次は勝敗をランダムではなく、プレイヤーの実力を反映したものにしてみます。
まず、プレイヤー全員に個々に変動しない真の「強さ」パラメータを設定します。
これはレートとは別で、シミュレーション開始時に各プレイヤーにランダムに値が決定され、1回のシミュレーション(つまり100戦)中は変わらない値としています。
値は区間 [0, 1) のランダムな値とします。
この「強さ」パラメータをチームで合計し、合計値が高い方のチームが 必ず勝つ 条件とします。
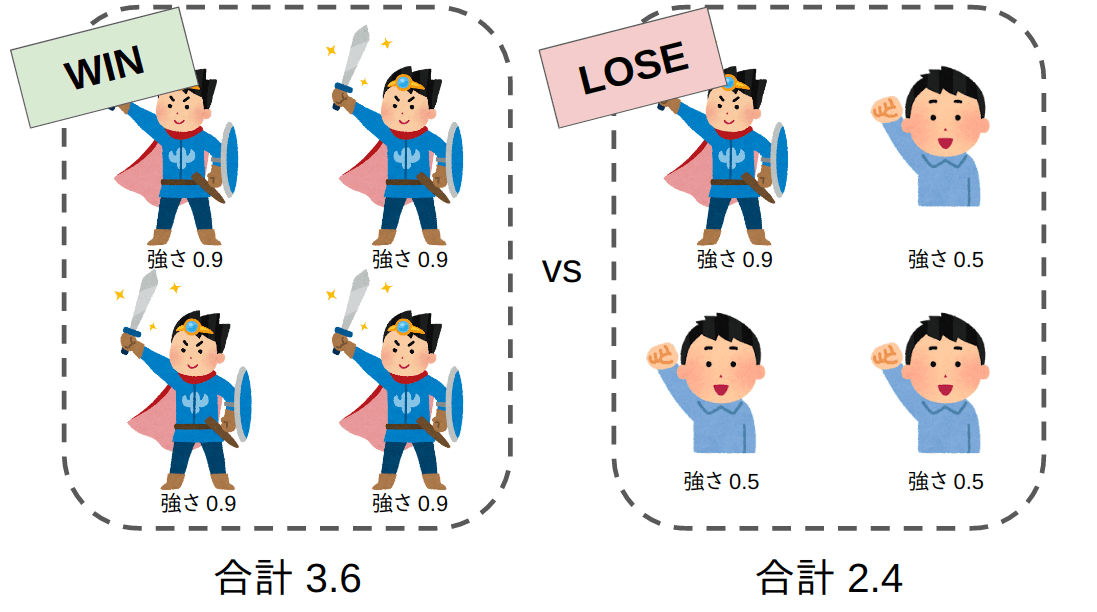
シミュレーション結果は次のようになりました。
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 15.75 | 3.93 | 0.83 |
| 定義B | 138.98 | 86.56 | 56.02 |
定義Aの方を見ると、シミュレーション1と比較してどの数値も下がっていることがわかります。
これは、プレイヤーの「強さ」が勝敗に強く影響するようになったため、偶然N連勝してその後N連敗するといった事象が発生しにくくなったためです。
定義B側はシミュレーション1に比べて大きく増加しています。
マッチング以外は運の要素が少ないため、「強さ」パラメータの高いプレイヤーほど順当にレートが上がっていきます。結果、強いプレイヤーほど連勝しやすくその後のマッチングで低レートのプレイヤーが味方に来る確率が上昇しているわけです。
3. 完全ランダムマッチ + 確率的勝利
先程のパターンでは強いチームは絶対に負けないルールでした。しかし、昨今オンライン対戦が行われるゲームは多少の運要素や不確定要素があり、実力が劣っていても勝つ場合もあるゲームが大多数です。は
そこで、チームの強さパラメータの和が高いチームでああれば、 ある一定確率 P で勝利する という条件にしてみましょう。
( p=0.5 の場合はシミュレーション1と、 p=1.0 の場合はシミュレーション2と同一になります。)
これでより実際のゲームに近づいた気がします。
p = 0.6 の場合
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.38 | 5.5 | 1.2 |
| 定義B | 97.59 | 52.58 | 28.19 |
p = 0.7 の場合
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 21.31 | 5.37 | 1.21 |
| 定義B | 104.25 | 57.88 | 32.22 |
p = 0.8 の場合
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 19.17 | 4.54 | 1.1 |
| 定義B | 113.08 | 65.66 | 38.98 |
当然ですが、結果はシミュレーション1と2の中間のものになりました。
4. 完全ランダムマッチ + 確率関数での勝利
先程のパターンではチームの実力が相手チームよりほんの僅かに上回ってる場合も、大きく上回っている場合も勝率は同じ確率でした。実際のゲームでは実力差があればあるほど勝率は偏るのが自然です。
4人チームの「強さ」パラメータの値域は区間 [0, 4) となっているので、勝利する確率を次の式で算出する条件としましょう。
チームAの勝利確率 = 0.5 + 0.1 * (チームAの強さ - チームBの強さ)
イロレーティングでは対数(指数)を利用していましたが、そこまで凝る必要も無いと判断し一次関数としました。
強さの差が最大となる、強さ合計がチームA 4.0 (厳密には最大値は4.0より極わずかに小さい)、チームB 0.0 の時にチームAの勝率は 0.9 となります。
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.6 | 5.33 | 1.32 |
| 定義B | 96.48 | 51.9 | 28.4 |
だいたい p=0.7 で固定した場合と同様の結果となりました。
プレイヤーの強さの分布次第で結果は変わってきますが、そこまで大きくは変わらないでしょう。(今回は [0, 1) の区間で一様分布)
5. 固定範囲でのマッチ
いよいよマッチングのルールに手を入れていきます。
まずシンプルに、プレイヤーを現在のレート順にソートし、何段階かのグループに分けます。

このグループ内でランダムにチームを編成し、同じグループ内の他チームと試合を行う条件とします。

上記のグループ = ランクと見なせば、同じランク内でしかマッチングされないゲームがこのパターンに近いと言えます。(今回はレートの順位でグループ分けを行ったので、厳密には一致はしていないですが)
グループ分けは1試合行われることに再度実施します。
何グループに分けるかで、マッチングの 幅 が決まりますので、いくつかのパターンでシミュレーションしてみます。
勝敗はシミュレーション4同様に確率関数で算出した確率で判定される条件とします。
グループ数4 = 1グループ64名
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.7 | 5.58 | 1.2 |
| 定義B | 28.77 | 15.36 | 8.69 |
グループ数8 = 1グループ32名
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.47 | 5.57 | 1.18 |
| 定義B | 15.53 | 8.72 | 4.95 |
グループ数16 = 1グループ16名
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.28 | 5.46 | 1.14 |
| 定義B | 10.99 | 5.45 | 2.98 |
グループ数32 = 1グループ8名
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.52 | 5.68 | 1.42 |
| 定義B | 7.96 | 3.73 | 1.96 |
定義A側はグループ数が変化してもとくに値に差は見られませんでした。
定義Bはグループ数が多くなるほど、別の言い方をするとグループ内の人数が少なくなるほど、懲罰マッチが発生しにくくなっています。
グループ数多い場合、連勝した際上のグループへと移動しやすい状況であると言えます。連勝後上のグループへ移動している状態だと、同じグループの他プレイヤーのレートも高いため、懲罰マッチが発生しにくいのだと考えられます。
逆にグループ数が少ない場合、グループ内で連勝しても上のグループへ上がる状況は少ないです。そのため、連勝しグループ内で上位のレートとなると確率的に弱い味方を引きやすくなってしまいます。
このことから、「固定幅」でのマッチングの場合、固定幅が広いほど定義Bとしての懲罰マッチ発生の確率が高くなることがわかりました。
6. 相対的に近いプレイヤーとマッチ
シミュレーション5のマッチング方式では、グループ上位のプレイヤーにおいて懲罰マッチが発生しやすくなることがわかりました。
固定範囲のマッチングでは連勝によりグループの上位プレイヤーになると、その後確率的に弱いプレイヤーとチームを組むことになるという課題があることがわかりました。
そこで、上記のようなマッチングを避けるため、自分と一定範囲のレートのプレイヤー同士がチームメンバーとなるようなマッチング方式を考えます。
イメージ的には下記の図のようなマッチングであることが望ましいと思われます。

少し複雑ですが、以下のようなシミュレーションとします。
- ランダムにプレイヤー1名をピックする
- マッチング範囲の初期値をXとする
- 1でピックされたプレイヤーのレートを
Rとし、区間[R-X, R+X]のレートのプレイヤーをリストアップする - リストアップされたプレイヤーの人数が2チーム編成できない場合はXを大きくし、繰り返す
- リストアップされたプレイヤーからランダムに2チームを編成し試合を行う
- 総試合数が規定数に達するまで1~5を繰り返す
プレイヤー間の試合数に差が出てしまいますが、全プレイヤーの総試合数は変わらないので、これまでのシミュレーションと結果を比較しても問題ないと判断しています。
Xは初期値を16とし、見つからなかったらさらに16ずつ増加させていきます。
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 定義A | 22.49 | 5.62 | 1.33 |
| 定義B | 4.68 | 1.95 | 0.9 |
はい、理想の結果が出ました。
シミュレーション5の固定幅の区間で区切った場合とくらべ、定義Bの値が現象していることがわかります。
これは連勝によりレートを上げたとしても、マッチング時に味方に来るプレイヤーのレートが上にも下にも一定範囲だからですね。
比較
定義Aの値はどちらのチームが勝つかの判定方法でしか大きく変化しませんでした。
つまり50%の確率でランダムに勝敗が決まる場合が連勝・連敗が連続しやすいという結果となりました。
定義Bに関して詳細に比較してみましょう。
4以降の各シミュレーションごとの結果を改めて並べてみます。
| 5連続 | 6連続 | 7連続 | |
|---|---|---|---|
| 4. 完全ランダムマッチ + 確率関数での勝利 | 96.48 | 51.9 | 28.4 |
| 5. 固定範囲でのマッチ(4グループ) | 28.77 | 15.36 | 8.69 |
| 5. 固定範囲でのマッチ(8グループ) | 15.53 | 8.72 | 4.95 |
| 5. 固定範囲でのマッチ(16グループ) | 10.99 | 5.45 | 2.98 |
| 5. 固定範囲でのマッチ(32グループ) | 7.96 | 3.73 | 1.96 |
| 6. 相対的に近いプレイヤーとマッチ | 4.68 | 1.95 | 0.9 |
4の完全ランダムマッチは言い換えれば1グループでの固定範囲でのマッチと同じ意味になります。
マッチング範囲を固定にした場合、マッチング範囲が広くなるほど懲罰マッチの発生率が上昇することがわかります。
8グループや16グループ程度の分割が実際のゲームに当てはまりそうです。(情報が公開されているゲームが少ないため主観です)
注目すべきはシミュレーション5とシミュレーション6の結果の差です。
プライヤーのランクやレートによる区分けを行わず、純粋の現在レートから上方向にも下方向にも近いユーザーでマッチングするシミュレーション6の方法では、シミュレーション5より数倍懲罰マッチの発生頻度が低いことがわかりました。
考察
やはり仮設の通り、固定幅によるマッチングではグループの境界に近づいたユーザーが懲罰マッチが発生しやすくなるということがわかりました。
懲罰マッチが永遠に続くわけではなく、一定数試合をこなしていくと解消されるように見えるのは上のグループへ移行したり、グループの上位から中間程度まで負けてレートを落とすことで解消されるためという解釈も我々の間隔と乖離しているものではないでしょう。
今回はグループ分けを現在レートの順位で行いました。
各グループの人数が均等になると試合のマッチングの実装が楽だったのでこの分け方にしていました。
ですが、いわゆるランク等によるグループ分けでもほぼ同等の結果が得られることは自明です。
余談:逆懲罰マッチ
当然、懲罰マッチが発生するのであれば、連敗した結果味方に強いプレイヤーが連続で来る、「逆懲罰マッチ」も発生することになります。定義を懲罰マッチの対称とするならば発生確率は懲罰マッチと同等になります。
SNS等でこちらの発生が話題になることはありませんが、片方だけを発生しやすいマッチングシステムを構築することは困難であるし、ゲーム運営サイドとしてもメリットが無いので行わないでしょう。
懲罰マッチは発生するとプレイヤーのフラストレーションがたまるため、悪とみなされる風潮がありますが、同等の確率で逆懲罰マッチも発生しており、たいていのプレイヤーは恩恵を受けていることでしょう。
懲罰マッチが限りなく発生しにくいマッチングシステムでは、この逆懲罰マッチも同様に発生しにくいことになります。果たしてこれが良いことなのか悪いことなのかは考察の余地がありそうです。
(プレイヤー心理的には懲罰マッチのほうが印象に残るので発生しないほうが良いような気はしますが)
まとめ
「同ランクのみとマッチング」等、ある固定範囲のプレイヤーで試合が組まれるゲームにおいて、懲罰マッチが発生しやすい傾向にあることがわかりました。
一方で純粋にレートが近いプレイヤーでマッチングさせる場合は上記よりも懲罰マッチの発生確率は低くなることがわかりました。
昨今懲罰マッチの存在が疑問視されるゲームタイトルにおいては、上記のようなランク等でマッチングのグループが振り分けられるような仕組みを採用している可能性があります。
注意書き
情熱のままに2日ほどでシミュレーションを行ったので、細部に不備がある可能性があります。
お手数ですがコメントでの指摘や、下記に掲載したシミュレーションコードを改良して自身で実行していただけると幸いです。
また、シミュレーションの回数や人数も使用したJupyterLabのスペックの関係で(k8s on RasPi)足りていない可能性があるので、その点もご容赦願います。
gist: https://gist.github.com/reireias/bb56dbb87432e1641ac4e95943c07f61
Discussion