Zenn
🖥️

計算効率上限界のバッチサイズを推定する方法[An Empirical Model of Large-Batch Training]

2023/12/23に公開
ディープラーニング
機械学習
#
深層学習
#
transformer
#
LLM
tech

本記事では以下の論文を解説する。
An Empirical Model of Large-Batch Training
https://arxiv.org/abs/1812.06162
これは、2018年にOpenAIから出た論文である。
Scaling Laws for Neural Language Modelsでも言及されている。

なにこれ？

  • 複数GPUで分散的に学習するとき有効に計算資源を活用するためにバッチサイズを上げることがある
  • そこでバッチサイズを増やして学習率を上げてを繰り返してもいいが、あるラインを超えると計算効率が著しく低下する
  • その限界となるバッチサイズはミニバッチ内の勾配分散と、全体の勾配から事前に推定可能
    • 以下の式で限界のバッチサイズを大まかに推定できる
    • \mathcal{B}_\text{simple} = \frac{\text{tr}(Σ)}{|G|^2}

具体的に

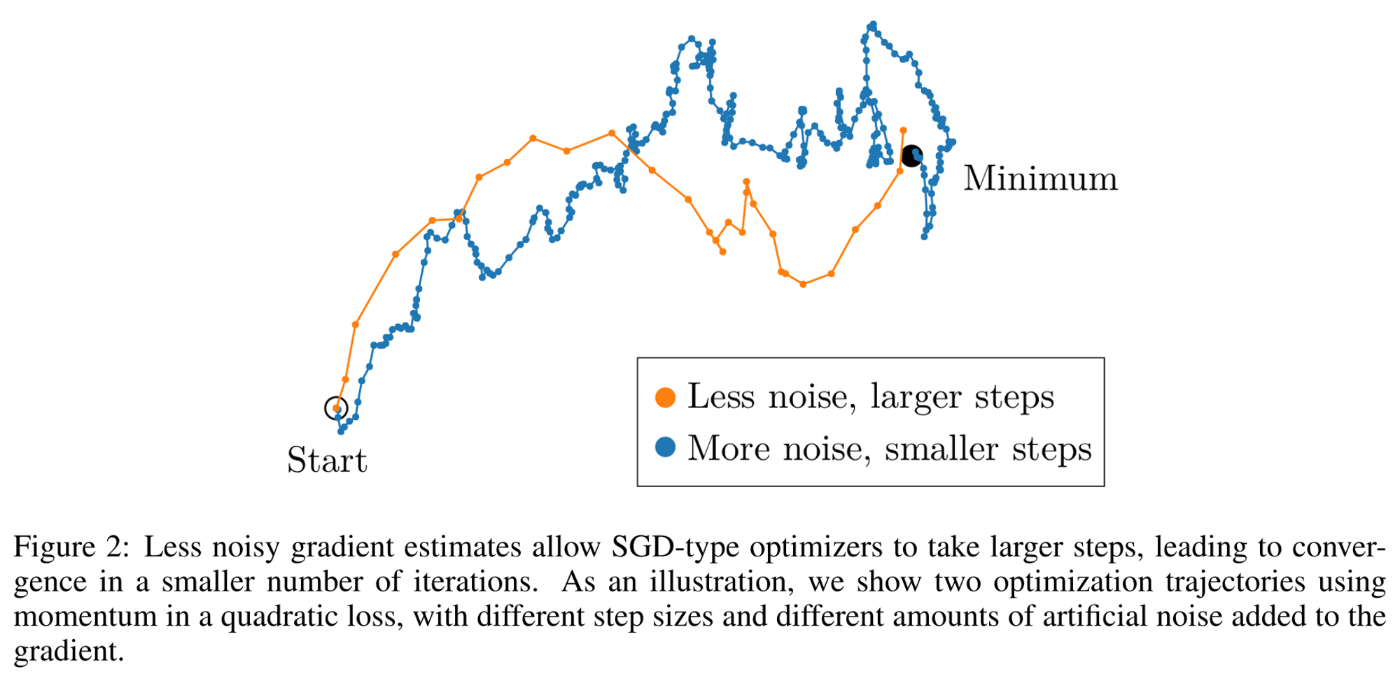
  • 学習時間（そのロスを達成するのに必要なoptimization steps）と計算資源（バッチサイズ）の図(Gradient accumulation=1)

  • バッチサイズを大きくすればノイズは小さくなり大きなSGDのステップを取れ、より少ないイテレーションで収束可

  • ただし、ある程度バッチサイズを大きくし勾配を正確に推測可能になると、それ以上バッチサイズを増やしても改善されない限界が現れる

    • これは上のグラフでも表れていて、青い領域の上側となるようなラインはバッチサイズを増やしてもあまり学習時間に改善が見られない

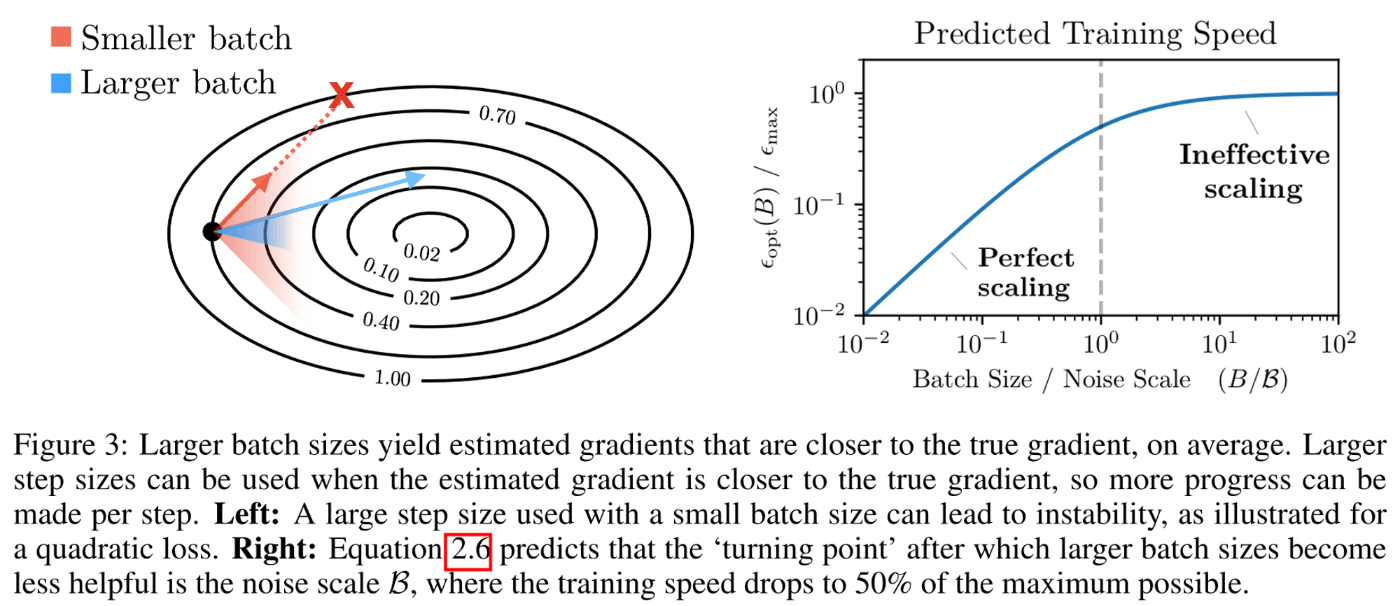
  • とあるラインを超えるてバッチサイズを増やしても学習率を増やせない事を表したグラフが下の右
    • バッチサイズBがB<\mathcal{B}の時はバッチサイズを増やすほど最適な学習率\epsilon_\text{opt}は増えていく
    • B>\mathcal{B}の時はバッチサイズを増やしても\epsilon_\text{opt}が増えない
    • \mathcal{B}の算出方法は以下で解説する

以下の様に変数を定義する

  • H：モデルパラメータθの真のヘッセ行列（真の勾配の勾配）
  • G：真の勾配
  • G_\text{est}：バッチサイズBのミニバッチの勾配
G_\text{est}(\theta) = \frac{1}{B} \sum_{i=1}^{B} \nabla_{\theta} L_{x_{i}}(\theta); \quad x_{i} \sim \rho
\begin{aligned} \Sigma(\theta) &\equiv \text{cov}_{x\sim p}(\nabla_{\theta} L_x(\theta)) \\ &= \mathbb{E}_{x\sim p}[(\nabla_{\theta} L_x(\theta))(\nabla_{\theta} L_x(\theta))^T] - G(\theta)G(\theta)^T \end{aligned}

モデルパラメータ\thetaを更新した後のロスは以下になる

E[L(θ − εG_\text{est})] = L(θ) − |G|^2 + \frac{1}{2} ε^2 (G^T HG + \frac{tr(HΣ)}{B} )

これを最小化する学習率\epsilonを求めると以下になる

ε_\text{opt}(B) = \argmin_ε E[L(θ − εG_\text{est})] = \frac{ε_max}{1 + \mathcal{B}_\text{noise}/B}

なお、\mathcal{B}_\text{noise}を以下のように定義する

\mathcal{B}_\text{noise} = \frac{\text{tr}(HΣ)}{G^T HG'}
\text{tr}(A) = \sum_{i=1}^{n} A_{ii}

ここで、\mathcal{B} \approx \mathcal{B}_\text{noise}である。
しかし、\mathcal{B}_\text{noise}はヘッセ行列と二回微分が入ってしまい、計算が難しいので以下のように近似する

\mathcal{B}_\text{simple} = \frac{\text{tr}(Σ)}{|G|^2}

よってこれを計算することで、ざっくりとバッチサイズの限界を推定することができる

PS: あくまで1学部生が調べたものであるので間違えたところがある可能性が有るのでその場合は是非教えてください。

Discussion