Zenn
🌏

GPS軌跡データをマップにマッチングする「Fast Map Matching」とは？

2023/07/23に公開
Python
#
gis
#
gps
#
mapmatching
tech

Map Matching とは

基本的にはGPSのデータ点を道路上に移動させることをMap Matching と呼びます．
これにより緯度経度の系列から車両がどの経路を走ったかを判定できます．

白い点がGPSデータ，赤線が道路上にマッチングしたあとの経路

本記事では，いくつかあるマップマッチング手法の中でも，GPSデータを使った論文でよく見るFast Map Matching (FMM) の解説と使い方について書いています．

なお，ほかの方法としては，MapboxがMap Matching API を出しているみたいです．
https://qiita.com/keijipoon/items/58ad450c87604c5a3052

Fast Map Matching (FMM) とは

2018年に公開された論文で提案されたマップマッチング手法です．

Can Yang and Gyozo Gidofalvi, Fast map matching, an algorithm integrating hidden Markov model with precomputation, International Journal of Geographical Information Science, Vol. 32, No. 3, pp. 547-570, 2018.

2009年に隠れマルコフモデル (HMM) を用いたマップマッチング手法が提案されて以来，多くの研究がHMMを用いた手法を研究しており，FMMもHMMを用いています．

FMMの処理の流れの概要は以下のとおりです．

  1. 事前計算
    • 道路ネットワーク内のすべてのノード間の最短距離を事前に計算してテーブル形式で持っておきます．そのテーブルはUpper Bounded Origin Destination Table (UBODT) と呼ばれます．（詳細はAppendixに）
  2. HMMと事前計算を統合したマップマッチング
    • まず，GPS軌跡のある点pに対して，マッチングする候補となるエッジを探索します．これにはKNNを使います．点pを中心とする辺の長さが2rの正方形に交わるエッジを抽出し，その各エッジに対して点pからの垂直距離を計算し，距離が短いほうからk個のエッジを候補とします．
    • 次に，HMMを用いてエッジの候補から最適なエッジ（つまり経路）を推測します．エッジの遷移確率と，実際に観測されるGPS点の出力確率は次のように定義します．
      • 遷移確率：ノード間のユークリッド距離でUBODTから検索する最短距離を割ったもの
      • 出力確率：平均0，標準偏差GPS_error（GPS誤差）に従う正規分布
    • そしてビタビアルゴリズムを用いて尤もらしいエッジの系列（つまり経路）を推定します
    • 推定したエッジの系列には経路に相当するすべてのエッジは含まれていないため，UBODTを用いて間のエッジを検索し，経路を完成させます
  3. 逆戻りするような経路の対処
    • 逆戻りするような経路にはペナルティを与えて不自然な経路にならないようにします

Fast Map Matching のインストール

FMMはオープンソースでGitHubに公開されています．
本記事ではUbuntuでの使用を想定していますが，WindowsやMacにもインストールできるようです．

Ubuntu 20.04 LTSでインストールしました．以下に記載の方法でインストールできます．
https://fmm-wiki.github.io/docs/installation/ubuntu.html

GDALのインストールで詰まる場合は，Stack Overflowに書いてある方法を行えばインストールできます．

Python を用いたFast Map Matching

FMMのGitHubには，Pythonを使った例やosmnxを使った例が挙げられています．（なお，Python2想定で書かれているので注意してください）

これらの例を参考に「軌跡データ（緯度経度の系列データ）を入力して，マップマッチングを行い，経路を出力する」というのをやってみます．

データの準備

軌跡データはPortoのタクシーデータを，道路ネットワークのデータはOpenStreetMapを使います．

軌跡データはtrain.csvとtest.csvがあります．データをダウンロードしてきてtrain.csvを読み込みます．

import numpy as np
import pandas as pd
import geopandas as gpd
import folium
from shapely.geometry import Polygon
from shapely import wkt
import osmnx as ox
import fm

data_path = "../data/porto/"
porto_taxi_data = pd.read_csv(f"{data_path}/train.csv")

OSMnxでPortoのOSMのデータからShapefileを作成します．GitHubのコードのとおりに実行します．

def save_graph_shapefile_directional(G, filepath=None, encoding="utf-8"):
    # default filepath if none was provided
    if filepath is None:
        filepath = os.path.join(ox.settings.data_folder, "graph_shapefile")

    # if save folder does not already exist, create it (shapefiles
    # get saved as set of files)
    if not filepath == "" and not os.path.exists(filepath):
        os.makedirs(filepath)
    filepath_nodes = os.path.join(filepath, "nodes.shp")
    filepath_edges = os.path.join(filepath, "edges.shp")

    # convert undirected graph to gdfs and stringify non-numeric columns
    gdf_nodes, gdf_edges = ox.utils_graph.graph_to_gdfs(G)
    gdf_nodes = ox.io._stringify_nonnumeric_cols(gdf_nodes)
    gdf_edges = ox.io._stringify_nonnumeric_cols(gdf_edges)
    # We need an unique ID for each edge
    gdf_edges["fid"] = np.arange(0, gdf_edges.shape[0], dtype='int')
    # save the nodes and edges as separate ESRI shapefiles
    gdf_nodes.to_file(filepath_nodes, encoding=encoding)
    gdf_edges.to_file(filepath_edges, encoding=encoding)
    
# Download by a bounding box
bounds = (-8.5584, -8.6607, 41.1854, 41.1230)  # east, west, north, south
x1, x2, y1, y2 = bounds
boundary_polygon = Polygon([(x1, y1), (x2, y1), (x2, y2), (x1, y2)])
G = ox.graph_from_polygon(boundary_polygon, network_type='drive')
start_time = time.time()
save_graph_shapefile_directional(G, filepath=f'{data_path}')

OpenStreetMapのサイトで範囲を調べると楽です．

FMMの実行

道路ネットワークデータ (shp) を読み込み，UBODTを作成します．

### Read network data
edges = gpd.read_file(f"{data_path}//edges.shp")
network = fmm.Network(f"{data_path}/edges.shp","fid","u","v")
print("Nodes {} edges {}".format(network.get_node_count(),network.get_edge_count()))
graph = fmm.NetworkGraph(network)


### Precompute an UBODT table

# Can be skipped if you already generated an ubodt file
ubodt_gen = fmm.UBODTGenAlgorithm(network,graph)
status = ubodt_gen.generate_ubodt(f"{data_path}//ubodt.txt", 0.02, binary=False, use_omp=True)
print(status)

### Read UBODT
ubodt = fmm.UBODT.read_ubodt_csv(f"{data_path}/ubodt.txt")

その後，FMMのパラメータであるKNNのkおよび，候補のエッジを決める際に使う正方形の辺の長さを決めるr (radius)，そしてGPSの誤差gps_errorを設定します．

### Create FMM model
model = fmm.FastMapMatch(network,graph,ubodt)

### Define map matching configurations
k = 8
radius = 0.003 # 300m
gps_error = 0.0005 # 50m
fmm_config = fmm.FastMapMatchConfig(k, radius, gps_error)

そして，下図のようなPortoのタクシーデータに対してマップマッチングを行います．

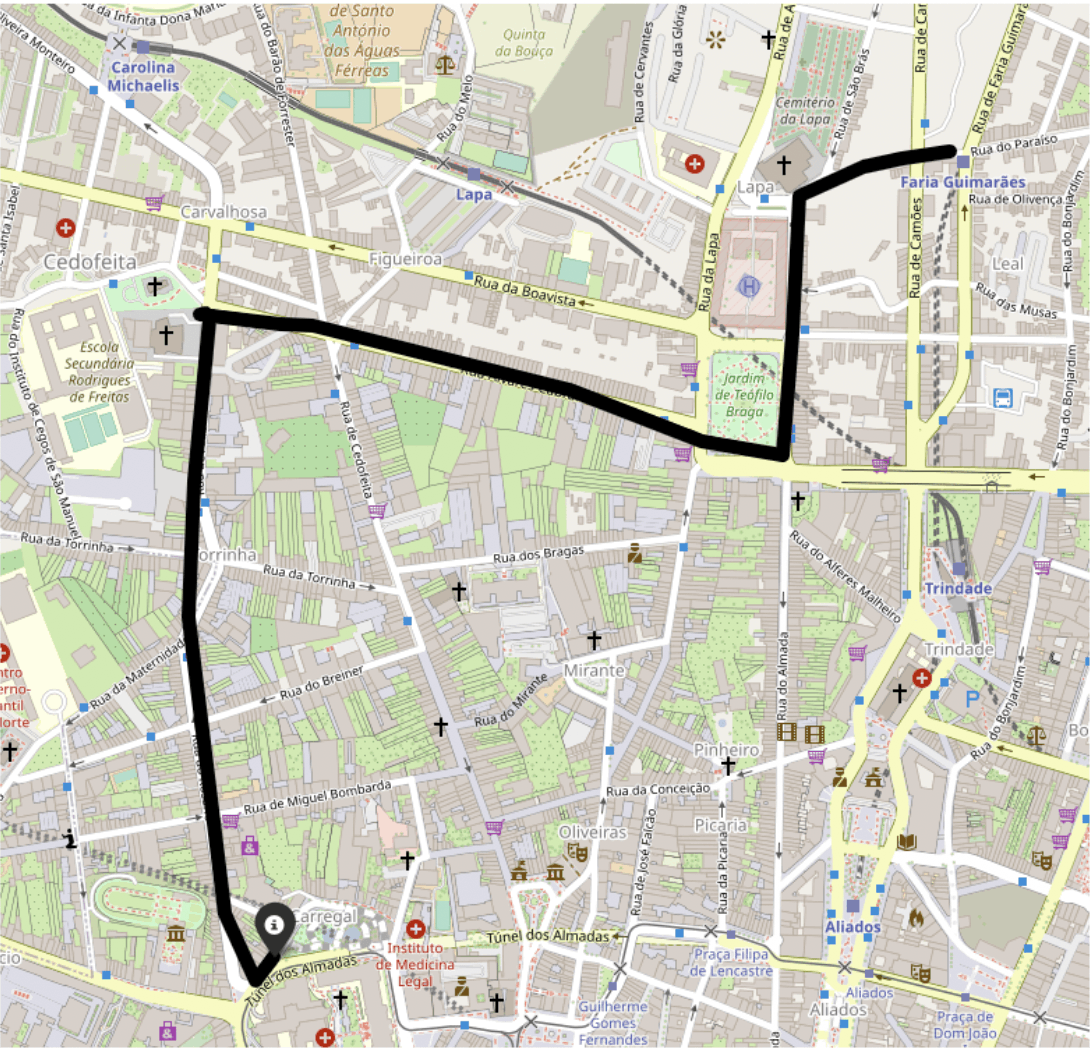黒線はGPSの点を結んだもの．アイコンが出発地点

coordinates = eval(porto_taxi_data.POLYLINE[10])
coordinates_str_list = [f"{lon} {lat}" for lon, lat in coordinates]
wkt = f"LINESTRING({','.join(coordinates_str_list)})" # well-known text (wkt) format

result = model.match_wkt(wkt, fmm_config)
matched_edges = edges[edges.fid.isin(result.cpath)]


# Visualization

# GPS trajectory
trajectory = pd.DataFrame(coordinates, columns=['lon', 'lat'])

center = [trajectory.lat.mean(), trajectory.lon.mean()]
m = folium.Map(location=center, tiles='OpenStreetMap', zoom_start=16)

folium.Marker(
    location=np.array(trajectory.loc[0, ['lat', 'lon']]),
    popup='Start',
    icon=folium.Icon(color='blue')
).add_to(m)

locations = []
for i in range(len(trajectory)):
    locations.append([trajectory.iloc[i].lat, trajectory.iloc[i].lon])
line = folium.PolyLine(locations=locations, weight=2, color='blue')
m.add_child(line)
m.add_child(folium.LatLngPopup())

# Matched edges
for _, row in matched_edges.iterrows():
    linestring = row['geometry']
    coords = [(lat, lon) for lon, lat in list(linestring.coords)]  
    folium.PolyLine(coords, color="red").add_to(m)

結果は，赤い経路のようになりました．ちゃんとマッチングできています．

ただ，FMMのGitHubにあるように，パラメータに結構センシティブな印象です．パラメータのkやrを大きくすれば精度は高くなりますが，その分時間がかかるので，用途に合わせて調整するのが良さそうです．

Appendix

事前計算の詳細

マップ（グラフ G）内のすべての最短経路のペアを計算します．ただし長さが閾値Δを超える場合は計算しません．それらをテーブル形式で保持します．

UBODTの各行が各ノードペアの最短経路であり，最短経路の計算にはダイクストラ法を用います．あるsource node から各ノードまでの最短距離を距離閾値Δに到達するまで更新していき，到達できたノードまでの最短距離distをテーブルUBODTに格納していきます．これをG内の全てのノードをsource node として繰り返します．なお，UBODTの1行は以下のように定義されるRとしています．

R(n_o,n_d)=(n_0,n_d,next_n,next_e,prev_n,dist)

UBODTが作成できたら，UBODTをハッシュテーブルに変換します．(no, nd)をキー，それ以外を値とします．これにより任意のノード間の最短距離を効率的に検索できます．また検索を繰り返し行うことでノード間の経路を構築することもできます．

Discussion