【Unity】プロジェクション行列を改造して遊ぶ【URP】

はじめに

Universal Render Pipelineは、ビュー行列やプロジェクション行列といったカメラの行列を簡単に書き換えることができます。

今回は、プロジェクション行列についての理解を深めることを目的として、
行列を書き換えたときの3Dモデルの変化を観察してみようと思います。

今回は、以下の3パターンについて実験してみます。

1. プロジェクション行列の $m_{11}$ を書き換える
2. プロジェクション行列の $m_{00}$ を書き換える
3. プロジェクション行列の $m_{33}$ を書き換える

環境

Unity 2021.3.9f1
Universal RP 12.1.7
Windows 10

3Dモデルが画面に表示されるまで

カメラでオブジェクトを映す

3Dモデルをカメラで映すと、ゲーム画面上に3Dモデルが表示されます。

プロジェクション座標変換

3Dモデルを画面に表示する時、
「カメラが映す空間(ビュー空間)をクリップ空間に変換する」
という座標変換がUnity内部で行われています。

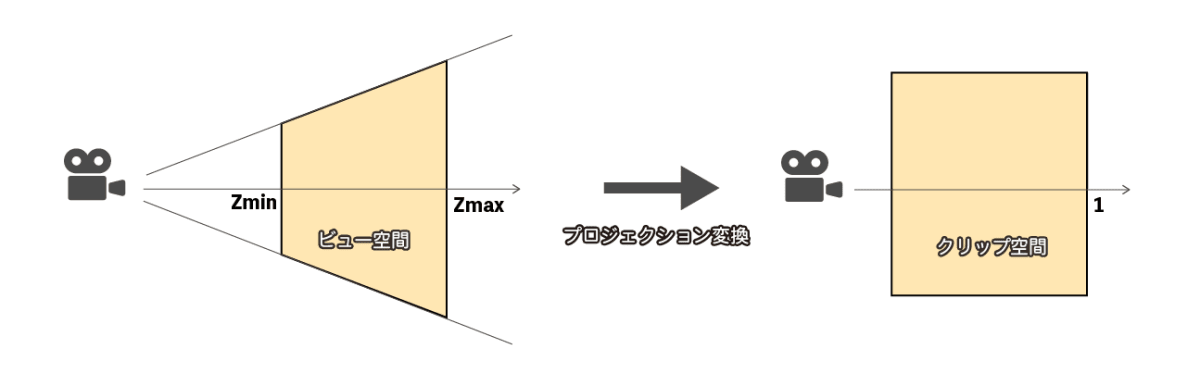
この変換は、プロジェクション行列を用いて行われます。
行列はFrameDebuggerから確認できます。

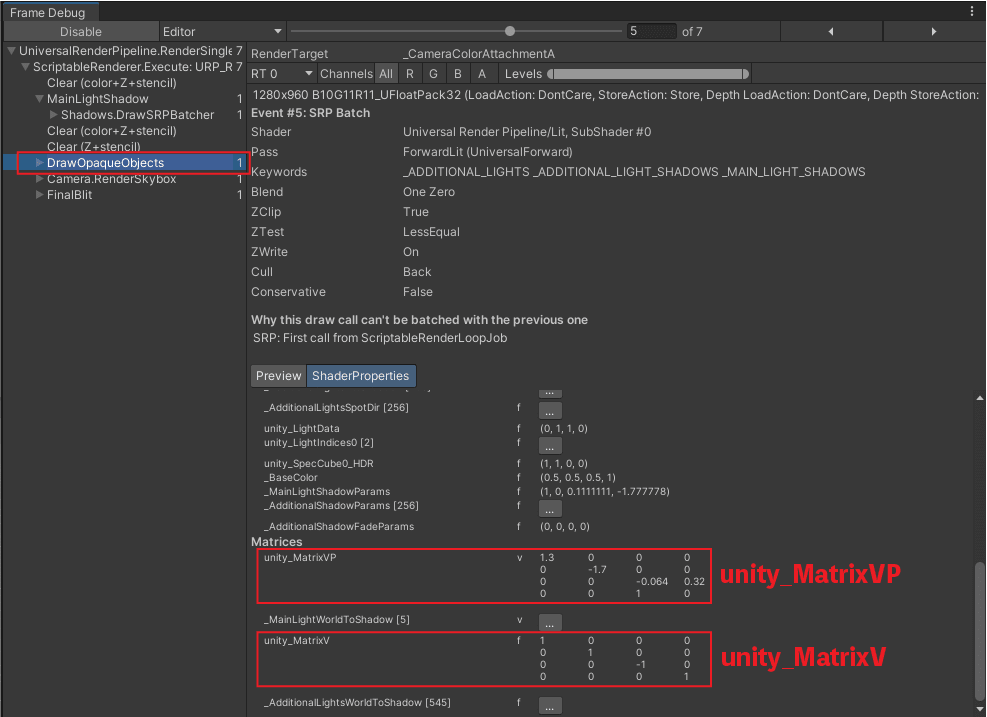
unity_MatrixV は、ビュー行列、
unity_MatrixVP は、ビュー行列とプロジェクション行列を乗じたものになります。

プロジェクション行列は、以下のような形になっています。

$$\begin{pmatrix} m_{00} & 0 & 0 & 0 \\ 0 & m_{11} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & 1 & 0 \end{pmatrix}$$

プロジェクション行列を改造してみる

次に、行列を書き換えた際の画面の変化を観察してみようと思います。

準備1 : シーンのセットアップ

カメラ位置を原点に合わせ、Z軸プラス方向を向けます

Cubeを作成し、位置(0, 0, 2)に配置します

この時、Gameビューの表示は以下のようになります

準備2 : URPを改造するための準備

Packagesフォルダの中に、URPのパッケージを配置します。
これで、URPのカメラ行列周りの処理を書き換え可能になります。

カメラ行列の実装箇所

ScriptableRenderer.csを見ると、カメラ行列の設定を行うメソッド SetCameraMatrices が定義されています。
Packages/com.unity.render-pipelines.universal@12.1.7/Runtime/ScriptableRenderer.cs

SetCameraMatricesの中を読むと、View行列やProjection行列を設定している個所があるので、ここを書き換えることでカメラ行列の書き換えができます。

ScriptableRenderer.cs

Matrix4x4 viewMatrix = cameraData.GetViewMatrix();
Matrix4x4 projectionMatrix = cameraData.GetProjectionMatrix();

// TODO: Investigate why SetViewAndProjectionMatrices is causing y-flip / winding order issue
// for now using cmd.SetViewProjecionMatrices
//SetViewAndProjectionMatrices(cmd, viewMatrix, cameraData.GetDeviceProjectionMatrix(), setInverseMatrices);
cmd.SetViewProjectionMatrices(viewMatrix, projectionMatrix);

行列を改造してみる

以下の3パターンについて実験してみます。

1. プロジェクション行列の $m_{11}$ を書き換える
2. プロジェクション行列の $m_{00}$ を書き換える
3. プロジェクション行列の $m_{33}$ を書き換える

$m_{22}$, $m_{23}$成分に関しては、画面上の変化が分かりにくいので省略します。

実験1 : プロジェクション行列のm11を反転させてみる

m11成分はy座標を加工する

プロジェクション行列の $m_{11}$ 成分は、頂点座標のy成分を加工する要素です。

$$\begin{pmatrix} x' \\ \red{y'} \\ z' \\ w' \end{pmatrix} = \begin{pmatrix} m_{00} & 0 & 0 & 0 \\ 0 & \red{m_{11}} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ \red{y} \\ z \\ 1 \end{pmatrix}$$

$x,y,z : ビュー空間の頂点座標$
$x',y',z' : クリップ空間の頂点座標$

プロジェクション行列のm11成分を反転させることで、変換後のy座標が反転します。

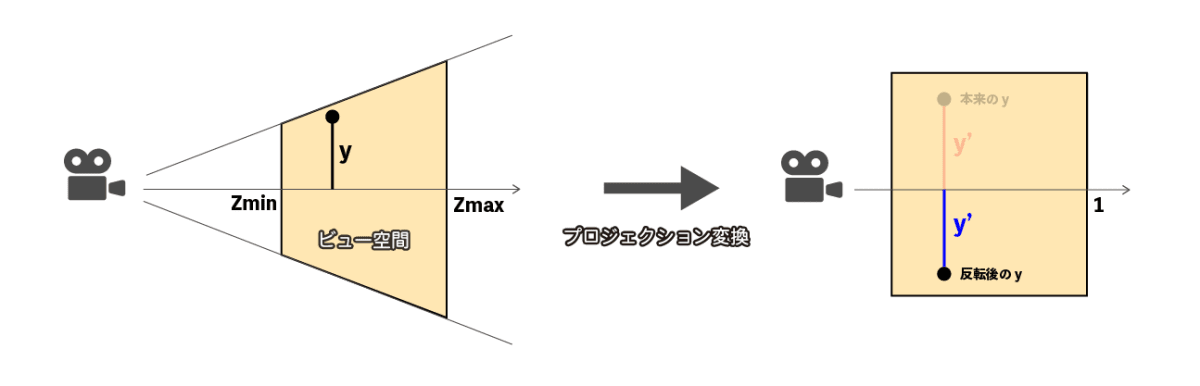
実験: m11を反転させる

projectionMatrixの $m_{11}$ 成分に-1を乗算します。

ScriptableRenderer.cs

Matrix4x4 viewMatrix = cameraData.GetViewMatrix();
Matrix4x4 projectionMatrix = cameraData.GetProjectionMatrix();
+ projectionMatrix.m11 *= -1;

結果

結果は、以下のようになります。
メッシュの上下が反転していますが、メッシュの裏表も逆になりました。

メッシュの表裏が反転する理由

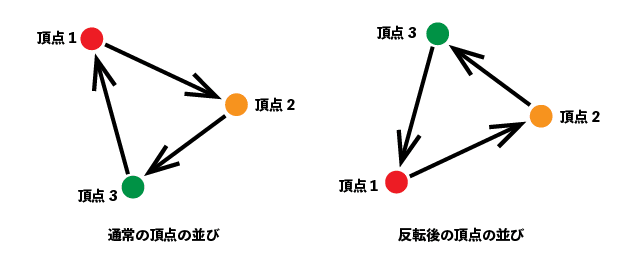
メッシュを描画する際、頂点が時計回りに並んでいる面が表面になります。
メッシュをY方向に反転させたことにより、頂点が並ぶ順番が逆になるため、表と裏が反転します。

実験2 : プロジェクション行列のm00も反転させてみる

プロジェクション行列の $m_{00}$ 成分は、頂点座標のx成分を加工します。

m00成分はx座標を加工する

$$\begin{pmatrix} \red{x'} \\ y' \\ z' \\ w' \end{pmatrix} = \begin{pmatrix} \red{m_{00}} & 0 & 0 & 0 \\ 0 & m_{11} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} \red{x} \\ y \\ z \\ 1 \end{pmatrix}$$

この要素を反転すると、クリップ空間のx座標が反転します

実験: m00とm11を反転させる

ScriptableRenderer.cs

Matrix4x4 viewMatrix = cameraData.GetViewMatrix();
Matrix4x4 projectionMatrix = cameraData.GetProjectionMatrix();
+ projectionMatrix.m11 *= -1;
+ projectionMatrix.m00 *= -1;

結果

3Dモデルの左右が反転し、メッシュの裏表が反転しました。

実験3 : プロジェクション行列のm33成分をいじる

計算式に注目

行列を書き換える前に、計算式を見てみます。
プロジェクション変換は、以下のような式で表現できます。

$$\begin{pmatrix} x' \\ y' \\ z' \\ \red{w'} \end{pmatrix} = \begin{pmatrix} m_{00} & 0 & 0 & 0 \\ 0 & m_{11} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & \red{1} & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ \red{z} \\ 1 \end{pmatrix}$$

$w'$に着目すると、

$$w'= z$$

となります。

W成分にz値がそのまま代入されます。

m32 成分に1が入っている理由

$m_{32}$ 成分に1が入っている理由

$$\begin{pmatrix} m_{00} & 0 & 0 & 0 \\ 0 & m_{11} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & \red{1} & 0 \end{pmatrix}$$

ビュー空間をクリップ空間に変換する式を導出すると、
計算の過程で、x, y, zそれぞれに関して、z値を用いた除算を計算する必要が出てきます。

z値をw成分に入れておくと、GPU側のW除算の仕組み上で、x, y, z をz除算を走らせることができます。

w成分にz値を入れると都合が良いので、$m_{32}$ 成分に1が入っているわけです。

W除算

ここで、4次元の座標$(x', y', z', w')$は、GPU側で$w'$で除算されてから画面上に表示されます。
$w'$が大きくなるほど、オブジェクトが小さく表示されます。

ここで、

$$w'=z$$

となっていました。

$z$が大きくなるほど(オブジェクトがカメラから離れるほど)、オブジェクトが小さく表示されます。

実験: m33成分を書き換える

次に、プロジェクション行列の $m_{33}$ 成分を書き換える、という実験を行ってみたいと思います。

$$\begin{pmatrix} x' \\ y' \\ z' \\ \red{w'} \end{pmatrix} = \begin{pmatrix} m_{00} & 0 & 0 & 0 \\ 0 & m_{11} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & \red{1} & \red{m_{33}} \end{pmatrix} \begin{pmatrix} x \\ y \\ \red{z} \\ \red{1} \end{pmatrix}$$

$w'$に着目すると、

$$w' = z + m_{33}$$

となります。

結果

$m_{33}$成分を増やすほど、立方体が小さくなります。

$m_{33}$成分を1増やす操作と、z座標を1増やす操作は、演算の結果が同じになります。

参考

https://zenn.dev/kazukisako/articles/czprfbcybbce

https://light11.hatenadiary.com/entry/2018/06/10/233954

http://marupeke296.com/DXG_No70_perspective.html