Zenn
⚡

【Unity】ライトプローブの影響を受ける雪エフェクトを作ってみた

2022/01/10に公開
particlesystem
tech

はじめに

降雪エフェクトをLight Probeで照らしてみました。
https://www.youtube.com/watch?v=rIh1HYrrvO4

サンプルプロジェクト

https://github.com/rngtm/Unity-LightProbeParticleSystem

環境

Unity 2022.1.0b2
Universal RP 13.1.3

実装について

通常、Particle Systemにライトプローブを適用すると、パーティクル全体に同じライトが適用され、全体が同じ色になってしまいます。(画像左)
今回の実装だと、パーティクルを部分的にライトで照らせるようになります。 (画像右)

ライトプローブから3Dテクスチャを作成し、パーティクル座標で3Dテクスチャをサンプリングするような実装になっています。

ライトプローブ(Light Probe)とは？

ライトプローブを配置すると、そこを通り抜ける光の情報を保存することができます。

オブジェクトへのライティングには、光を補間したものが利用されます。

上図では光を矢印形式で表していますが、実際は球面調和関数形式で表現されます。

ライトプローブのライティング

オブジェクトをシーンに配置すると、オブジェクトに最も近いライトプローブを利用して、ライティングが行われます。

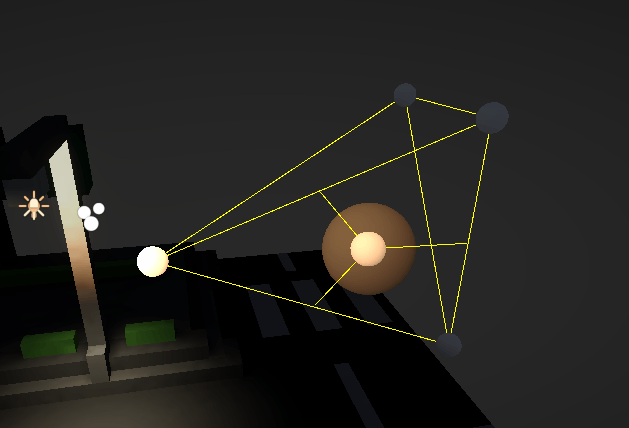
ParticleSystemにライティングを適用した場合は以下のようになります。

ある一点を基準にして最も近いライトプローブが選択されてライティングに使用されるため、雪全体が同じ色(不自然な見た目)になってしまいます。

今回のように広範囲に降らせるエフェクトでは、エフェクトの粒子ごとにライトプローブが選択される方が望ましいです。

パーティクル位置を利用したライティング

今回は、以下のような実装でパーティクル位置でライトプローブの色を反映させるようにしてみました。

  1. 空間を格子状に区切り、それぞれの格子点でライトプローブをサンプリングする
  2. サンプリング結果から3Dテクスチャを作成する
  3. パーティクルの中心座標を利用して3Dテクスチャをサンプリングし、パーティクルの色に反映する

この方法でライティングを行うと、以下のような結果になります。

実装1 : ライトプローブのサンプリング

LightProbes.GetInterpolatedProbeを利用することで、あるポイントを通過する光を取得できます。

LightProbes.GetInterpolatedProbe(position, null, out SphericalHarmonicsL2 sh);

光の情報は SphericalHarmonicsL2形式で取得でき、この中には球面調和関数の係数が格納されています。

拡散光の取得

ここで、雪を観察してみましょう。
雪に当たった白い光は乱反射を起こすので、白く見えます。

雪の粒子に光が当たると、乱反射を起こして四方八方に光が散らばります。(拡散光)

実装コード

SphericalHarmonicsL2(球面調和関数)のL0成分を取ることで、拡散光の強さを取得できます。

SphericalHarmonicsL2からL0成分を取得する例
    var r = sh[rgb: 0, coefficient: 0]; // 赤い光 (red)
    var g = sh[rgb: 1, coefficient: 0]; // 緑の光 (blue)
    var b = sh[rgb: 2, coefficient: 0]; // 青の光 (green)

実装2 : 3Dテクスチャの作成

光が届く領域をまるごと覆う形で箱を配置し、箱の中の領域をテクスチャ座標(0,0,0) ~ (1,1,1)として割り当てることを行います。
(Texture3Dなので、テクスチャ座標は3次元になります)

箱を格子状に区切り、それぞれの格子点で球面調和関数のL0をサンプリングします。

実装コード

空間を格子状に区切り、ライトプローブをサンプリングする実装例を以下に示します。

SHLattice.cs
Vector3 minPosition = transform.position - size / 2; // 箱の最小座標
Vector3 maxPosition = transform.position + size / 2; // 箱の最大座標

// 格子上に区切り、各点でライトプローブをサンプリングする
int index = 0;
for (int zi = 0; zi < grid.z; zi++)
{
    float tz = (float) zi / (grid.z - 1);
    float z = Mathf.Lerp(minPosition.z, maxPosition.z, tz);

    for (int yi = 0; yi < grid.y; yi++)
    {
        float ty = (float) yi / (grid.y - 1);
        float y = Mathf.Lerp(minPosition.y, maxPosition.y, ty);

        for (int xi = 0; xi < grid.x; xi++)
        {
            float tx = (float) xi / (grid.x - 1);
            float x = Mathf.Lerp(minPosition.x, maxPosition.x, tx);

            // ライトプローブをサンプリングする
            var p = new Vector3(x, y, z);
            LightProbes.GetInterpolatedProbe(p, null, out SphericalHarmonicsL2 sh);
            
            // ライトプローブの保存
            shTable[index] = sh;
            index++;
        }
    }
}

サンプリングしたライトプローブのL0成分を取り出し、Texture3Dに格納します。

ParticleLightReceiver.cs
Vector3Int grid = _shLattice.Grid;
int count = grid.x * grid.y * grid.z;
var shL0 = new Color32[count];
for (int i = 0; i < count; i++)
{
    var sh = _shLattice.ShTable[i];
    var r = sh[rgb: 0, coefficient: 0];
    var g = sh[rgb: 1, coefficient: 0];
    var b = sh[rgb: 2, coefficient: 0];
    shL0[i] = new Color(r, g, b);
}

_shTexture3D.SetPixels32(shL0);
_shTexture3D.Apply();

作成した3Dテクスチャは、マテリアルに渡しておきます。
MaterialPropertyBlock を使うことで、マテリアルインスタンスを複製せずにパラメータを渡すことができるので便利です。

ParticleLightReceiver.cs
_materialPropertyBlock.SetTexture(ShaderProperty._ShTex, _shTexture3D);

実装3 : パーティクルの色に反映

以下の手順で、パーティクル座標を元にTexture3Dから色を取得します。

  1. パーティクルの中心座標をシェーダーへ流す (Custom Vertex Streams)
  2. パーティクルの中心座標から、3Dテクスチャ座標を計算 (ShaderLab)
  3. テクスチャ座標を利用して、3Dテクスチャから色を取り出す (ShaderLab)

パーティクルの中心座標を渡す(Particle System)

Particle System側のCustom Vertex Streams へ Center を登録します。
これにより、シェーダー側からパーティクルの中心座標が取れるようになります。

TEXCOORD0.zw|x と表示されていますが、
これは頂点アトリビュートの TEXCOORD0.zw と TEXCOORD1.x を参照することで、
パーティクルの中心座標が取れることを表しています。

パーティクルの中心座標の取得(ShaderLab)

頂点属性の構造体にTEXCOORD0とTEXCOORD1を定義しておきます。

struct appdata
{
    float4 vertex : POSITION; // 頂点座標
    half4 color : COLOR; // 頂点カラー
    float4 texCoord0 : TEXCOORD0; 
    float4 texCoord1 : TEXCOORD1;
};

頂点シェーダー内では以下のように記述することで、パーティクルの中心座標を取得できます。

v2f vert (appdata v)
{
    // パーティクル中心座標 (Custom Vertex Streamsで指定した座標を取り出す)
    float3 worldPosition = float3(v.texCoord0.zw, v.texCoord1.x);

実装例

パーティクル中心座標を利用して、3次元テクスチャをサンプリングする実装例を以下に示します。

struct appdata
{
    float4 vertex : POSITION; // 頂点座標
    half4 color : COLOR; // 頂点カラー
    float4 texCoord0 : TEXCOORD0; 
    float4 texCoord1 : TEXCOORD1;
};
            
v2f vert (appdata v)
{
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.texCoord = TRANSFORM_TEX(v.texCoord0.xy, _MainTex);

    // パーティクル中心座標 (Custom Vertex Streamsで指定した座標を取り出す)
    float3 worldPosition = float3(v.texCoord0.zw, v.texCoord1.x); 

    // テクスチャ座標を復元
    float3 shCoord = (worldPosition - _MinPosition) / (_MaxPosition - _MinPosition);

    // 0 ~ 1の範囲に収める
    shCoord = saturate(shCoord);

    // ライト情報を取り出す
    float4 light = tex3D(_ShTex, shCoord);
    
    o.color = v.color * light;
    return o;
}

最終的な表示

以下のような、ライトプローブの影響を受ける雪エフェクトが作れます。

詳しい作り方が気になる方は、以下のサンプルプロジェクトをご覧ください。
https://github.com/rngtm/Unity-LightProbeParticleSystem


おまけ: SphericalHarmonicsL2の中身

SphericalHarmonicsL2 の中には、27個のfloat値が入っています。
これらは、球面調和関数の係数です。

SphericalHarmonicsL2.cs
    private float shr0;
    private float shr1;
    private float shr2;
    private float shr3;
    private float shr4;
    private float shr5;
    private float shr6;
    private float shr7;
    private float shr8;
    private float shg0;
    private float shg1;
    private float shg2;
    private float shg3;
    private float shg4;
    private float shg5;
    private float shg6;
    private float shg7;
    private float shg8;
    private float shb0;
    private float shb1;
    private float shb2;
    private float shb3;
    private float shb4;
    private float shb5;
    private float shb6;
    private float shb7;
    private float shb8;

球面調和関数を利用した光の近似

ライトプローブを通過する光を表現する方法について考えてみます。

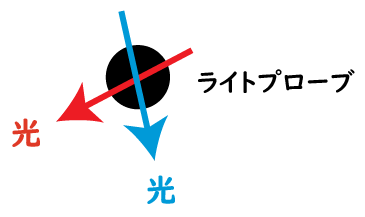
ライトプローブを中心とする球面を通過する光が分かれば、ライトプローブを通過する光が分かります。

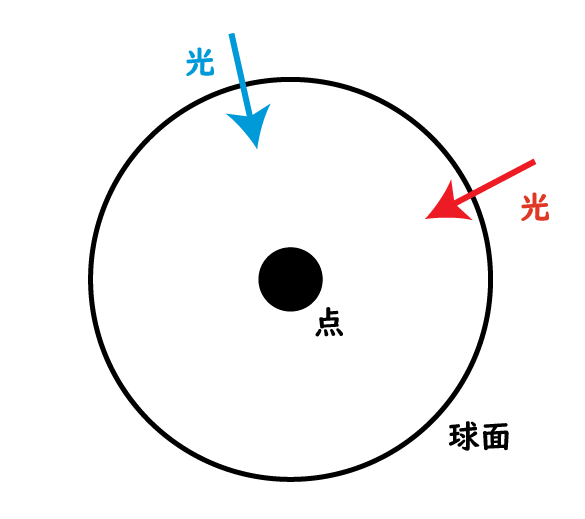
球面を通過する光をすべて扱おうとすると、大量のデータが必要になります。
例えば、100個の光線が球面を通過する場合、100個のベクトルが必要になります。
これらの光線すべてをコンピューター上で扱うのはデータが多すぎて現実的ではありません。

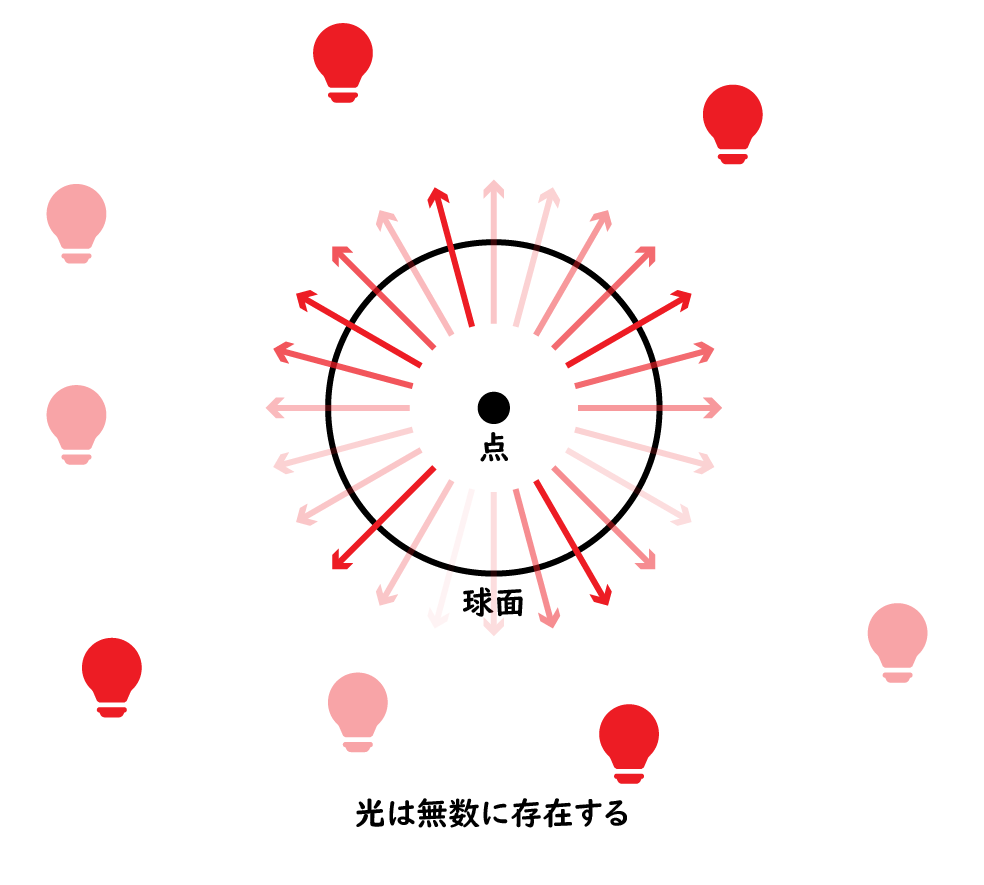
そこで、光線の集まりを球面上の分布関数f(\theta, \phi)として扱います。

この関数をそのまま扱う場合も、やはり多くのデータが必要になります。
そこで、f(\theta, \phi)を、ある別の関数Y_{lm}(\theta, \phi) の足し合わせによって
表現するということを行います。

f(\theta, \phi) = \sum_{l = 0}^{\infty} \sum_{m = -l}^{l} \color{green} a_{lm} \cdot \color{black} Y_{lm}(\theta, \phi)

関数 Y_{lm}(\theta, \phi) のことを、球面調和関数と呼びます、
\color{green} a_{lm} は球面調和関数の係数です。

球面調和関数は、以下のような形をしています。

Wikipedia「球面調和関数」より引用

球面調和関数を利用した光の復元

ライトプローブに入ってくる光の分布 f(\theta, \phi) は、球面調和関数 Y_{lm}(\theta, \phi) 、係数 a_{lm}を用いて
以下のように表せます。

f(\theta, \phi) = \sum_{l = 0}^{\infty} \sum_{m = -l}^{l} a_{lm} \cdot Y_{lm}(\theta, \phi)

重み a_{lm} を乗じて球面調和関数Y_{lm}(\theta, \phi)を足し合わせることで、
ライトプローブに入ってくる光の分布f(\theta, \phi) を復元できる、という事を意味しています。

Unityでの球面調和関数

Unity上では、球面調和関数の係数を9個を打ち切っています。
例えば、shr0 ~ shr8 は赤い光の係数 a_{lm} を表しています。

SphericalHarmonicsL2.cs
    // L = 0
    private float shr0; 
    
    // L = 1
    private float shr1; 
    private float shr2;  
    private float shr3; 

    // L = 2 
    private float shr4; 
    private float shr5; 
    private float shr6; 
    private float shr7; 
    private float shr8;

数式的に書くと、以下のような式になります。
無限の計算を途中で打ち切っているので、近似値になります。

f(\theta, \phi) \approx \sum_{l = 0}^{2} \sum_{m = -l}^{l} \color{green} a_{lm} \color{black} \cdot Y_{lm}(\theta, \phi)

上式の \color{green} a_{lm} は、SphericalHarmonicsL2.cs の shr0 ~ shr8 に対応しています。

拡散光

ライトプローブの拡散光を取得するとき、以下のような実装を行いました。

SphericalHarmonicsL2からL0成分を取得する例
    var r = sh[rgb: 0, coefficient: 0]; // 赤い光 (red)
    var g = sh[rgb: 1, coefficient: 0]; // 緑の光 (blue)
    var b = sh[rgb: 2, coefficient: 0]; // 青の光 (green)

これは、球面調和関数のL0成分を取得しているコードで、以下の式の a_{00} がこれに相当します。

f(\theta, \phi) \approx \sum_{l = 0}^{2} \sum_{m = -l}^{l} \color{green} a_{l,m} \color{black} Y_{l,m}(\theta, \phi) = \color{red} a_{00} \color{black} Y_{00}(\theta, \phi) + a_{1,-1} Y_{1,-1}(\theta, \phi) + a_{1,0} Y_{1,0}(\theta, \phi) + ...



Y_{00}(\theta, \phi) は球面上で一様に分布する関数で、以下のように表される関数です。

Y_{00}(\theta, \phi) = \frac{1}{2} \sqrt{\frac{1}{\pi}}

参考書籍

https://www.amazon.co.jp/リアルタイムレンダリング-Real-Time-Rendering-Fourth/dp/4862464580

Discussion