はじめに
量子コンピュータの理論によく現れる量子ビットの Bloch sphere 表示はヒルベルト空間 \mathbb{C}^2 上のベクトル表記と 2 次元球面 S^2 上の極座標表示がシレっと同一視されていることが多いため, Hopf fibration との関係を説明して両者の座標成分をまじめに計算した.
- この記事では量子アルゴリズムの紹介はしない.
- ヒルベルト空間という言葉は出て来るが, 有限次元の線形代数だけで関数解析は使わない.
- 量子力学からの要請については参考文献を示すが, 物理的背景の説明まではしない.
対象読者
- 線形代数や複素数平面の極座標表示を知っている方.
- 数学的な内容に興味のある方 (数学専門の方には退屈かもしれません).
本記事で扱う量子力学の基本事項
Hopf fibration の言葉で解釈できる量子力学の基本事項をまとめる.
複素ヒルベルト空間
本記事では多重量子ビット (n 量子ビット) で表される量子状態を扱うが, 量子力学の要請によって複素ヒルベルト空間 \mathbb{C}^N (n 量子ビットで表現できる計算基底のサイズが N=2^n)を考える. 量子力学における複素ヒルベルト空間の役割について詳細は量子力学の教科書を参照.
本記事では複素ヒルベルト空間 \mathbb{C}^N の元 v, w の内積を \langle v, w \rangle を使って表す.
物理量の期待値
量子力学からの要請で, 物理量は複素ヒルベルト空間 \mathbb{C}^N の自己共役演算子 A で表される. 本記事では複素ヒルベルト空間 \mathbb{C}^N は有限次元であるため, A は以下を満たす複素数値 N\times N 行列 (エルミート行列) である.
左辺の行列は A の各成分の複素共役をとってから転置してできる行列を表す.量子力学によると状態ベクトル v \in \mathbb{C}^N における物理量 A の期待値 \langle A \rangle が以下の式で計算される.
\langle A\rangle = \langle v, Av \rangle.
右辺は量子力学のブラケット記法 v=\Ket{\varphi} で \Bra{\varphi}A\Ket{\varphi} と書かれるものである.
射影演算子
状態ベクトル v \in \mathbb{C}^N に対して射影演算子 v\otimes \overline{v}:\mathbb{C}^N \longrightarrow \mathbb{C}^N を以下のように定義する. w \in \mathbb{C}^N に対して,
v \otimes \overline{v}(w):=\langle v, w \rangle v.
-
\overline{v} でベクトル v の各成分の複素共役をとってできるベクトルを表す. 右辺で v は内積の左側にあるので複素共役をとっている.
- 射影演算子 v \otimes \overline{v} はベクトル w の v 方向成分を取り出す線形写像である.
- 射影演算子 v \otimes \overline{v} は量子力学のブラケット記法 v=\Ket{\varphi} で \Ket{\varphi}\Bra{\varphi} と書かれる.
量子力学によると物理量を表すエルミート行列 A の固有値 a は物理量が観測によってとりうる値である. ボルンの確率規則によると, 状態ベクトル w であらわされる量子状態において物理量 A が a の値をとる確率は, a の固有空間 V_a の正規直交基底 v_1, \dots, v_l を使って,
\sum_{i=1}^{l}|v_i \otimes \overline{v_i}(w)|^2
と表される. ベクトル w を固有空間 V_a へ射影したベクトルの長さの 2 乗となっている.
複素ヒルベルト空間の球面と複素射影空間
量子力学からの要請で, 量子状態を与えるベクトル v = (z_1,\dots, z_{N}) \in \mathbb{C}^{N} は長さ 1 に制限されたものだけを考える. このようなベクトルの集合は複素ヒルベルト空間 \mathbb{C}^{N} の球面 S^{2N-1} をなす (2N-1 は \mathbb{C}^{N} を実ベクトル空間 \mathbb{R}^{2N} とみなしたときの球面の次元).
S^{2N-1}:=\{ v \in \mathbb{C}^{N} \:|\: |v| =1 \}.
S^{2N-1} は規格化されたベクトルを集めた集合ではあるが, v \in S^{2N-1} に対して位相因子 (phase factor) の異なる同じ量子状態を表すベクトルたち e^{i\alpha}v, \alpha \in [0, 2\pi) を区別する.
v = (z_1,\dots, z_{N}) \in \mathbb{C}^{N} に対してその複素スカラー倍で得られるすべてのベクトルを集めた集合を v が生成する複素 1 次元部分空間 [v] という.
[v] := \{ zv \in \mathbb{C}^{N}\:|\: z \in \mathbb{C} \}.
v = (z_1,\dots, z_{N}) \in \mathbb{C}^{N} が生成する複素 1 次元部分空間を集めてできる集合を複素射影空間 \mathbb{C}P^{N-1} という.
\mathbb{C}P^{N-1} := \{[v] \:|\: v \in \mathbb{C}^{N} \}.
量子力学では量子状態を表すベクトルの複素数スカラー倍が同じ量子状態を表すので, 数学的には量子状態は複素射影空間 \mathbb{C}P^{N-1} の元で与えられる. \mathbb{C}P^{N-1} では phase の異なる同じ量子状態を表すベクトルたちを区別しない.
多重量子ビットでの Hopf fibration
本節では, 一般の多重量子ビットでの Hopf fibration について述べる. 多重量子ビットでは Hopf fibration は定義できるが, 後で説明する 1 量子ビットの Bloch sphere 表示のような単純な表示はできないことに注意する.
Hopf fibration
複素ヒルベルト空間 \mathbb{C}^{N} の規格化されたベクトルと複素射影空間 \mathbb{C}P^{N-1} の元との対応
f: S^{2N-1} \longrightarrow \mathbb{C}P^{N-1}
f(v):=[v] を Hopf fibration という. Hopf fibration は v の射影演算子 \pi(v) = v \otimes \overline{v} を対応させているとみなすことができる. なぜなら v \otimes \overline{v}(\mathbb{C}^N) = [v] (v \otimes \overline{v} の像は v が生成する複素 1 次元部分空間) であり, v \in S^{2N-1} (|v|=1) に許された任意の複素数倍 e^{i\alpha}v (\alpha \in \mathbb{R}), が同じ射影演算子 e^{i\alpha}v \otimes \overline{e^{i\alpha}v} = v \otimes \overline{v} を定めるからである.
Hopf fibration は数学とくに幾何学でとても由緒正しいもので, 文献が山ほどある. 詳しい解説は例えば Wikipedia やその中の文献がある.
1 量子ビットでの Hopf fibration
1 量子ビットでの Hopf fibration は複素 1 次元射影空間 \mathbb{C}P^1 が 2 次元球面 S^2 と同一視できることから, 視覚的にわかりやすい成分表示をすることができる.
パウリ行列
以下の複素行列をとる.
\sigma_1 = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix},\;
\sigma_2 = \begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix},\;
\sigma_3 = \begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}.
これらの行列はパウリ行列と呼ばれ, 量子力学や量子コンピュータの理論で基本的な役割を担っている. これらの行列の実数線形結合をとることで任意のトレース 0 の複素 2\times2 エルミート行列を表せる. 以下 \alpha_1, \alpha_2, \alpha_3 は実数.
\alpha_1 \sigma_1 + \alpha_2 \sigma_2 + \alpha_3 \sigma_3 =
\begin{pmatrix}
\alpha_3 & \alpha_1 - i \alpha_2 \\
\alpha_1 + i \alpha_2 & -\alpha_3
\end{pmatrix}.
さらに複素 2\times2 単位行列 I も使えば, 任意の複素 2\times2 エルミート行列を表せる. 以下 \alpha_0, \alpha_1, \alpha_2, \alpha_3 は実数.
\alpha_0 I + \alpha_1 \sigma_1 + \alpha_2 \sigma_2 + \alpha_3 \sigma_3 =
\begin{pmatrix}
\alpha_0 + \alpha_3 & \alpha_1 - i \alpha_2 \\
\alpha_1 + i \alpha_2 & \alpha_0 -\alpha_3
\end{pmatrix}.
1 量子ビットでは Hopf fibration は S^3 の点を \mathbb{C}P^1 の点に写すが, 以下で説明するように射影演算子や立体射影を使って \mathbb{C}P^1 の点 を S^2 の点に対応させることで, 1 量子ビットでの Bloch sphere 表示が得られる.
射影演算子による対応
v=(z_1, z_2) として射影演算子 v \otimes \overline{v}: \mathbb{C}^2 \longrightarrow \mathbb{C}^2 を行列表示する.
v \otimes \overline{v} =
\begin{pmatrix}
z_1 \overline{z_1} & z_1 \overline{z_2} \\
z_2 \overline{z_1} & z_2 \overline{z_2}
\end{pmatrix}.
この行列は複素 2\times2 エルミート行列なので, 上記のように実数 \alpha_0, \alpha_1, \alpha_2, \alpha_3 をとって,
v \otimes \overline{v} = \alpha_0 I + \alpha_1 \sigma_1 + \alpha_2 \sigma_2 + \alpha_3 \sigma_3
と表せる (量子状態 v のブロッホ表現). 線形結合の係数と行列成分との対応は以下のようになっている.
\begin{aligned}
2\alpha_0 &= |z_1|^2 + |z_2|^2 = \text{tr}(v \otimes \overline{v}) = |z|^2 = 1, \\
2\alpha_1 &= 2\text{Re}(z_2 \overline{z_1}), \\
2\alpha_2 &= 2\text{Im}(z_2 \overline{z_1}), \\
2\alpha_3 &= |z_1|^2 - |z_2|^2.
\end{aligned}
このとき以下の写像 \pi:S^3 \longrightarrow S^2 が Hopf fibration を S^2 で表示したものとなっている.
\pi(z_1, z_2):= (2\alpha_1, 2\alpha_2, 2\alpha_3).
以下に注意する.
-
\mathbb{C}P^1 と S^2 とは対応 g:v\otimes \overline{v} \longmapsto (2\alpha_1, 2\alpha_2, 2\alpha_3) によって同一視される.
-
\pi=g \circ f, すなわち \pi は Hopf fibration f を S^2 で表示したものとなっている.
Bloch sphere
写像 \pi を以下のように極座標表示することで, 量子コンピュータの理論でよく利用される Bloch sphere 表示が得られる.
極座標表示
1 次元複素平面 \mathbb{C} 上の極座標表示 (z=re^{ia}, r, a \in \mathbb{R}) を使って (z_1, z_2) \in \mathbb{C}^2 を表す.
\begin{pmatrix}
z_1 \\
z_2
\end{pmatrix} = \begin{pmatrix}
r_1 e^{ia_1} \\
r_2 e^{ia_2}
\end{pmatrix}.
量子力学からの要請で状態ベクトルは S^3 上 (|z_1|^2 + |z_2|^2=1) で考えているので, (z_1, z_2) は実数 a_3 を使って以下のように表せる.
\begin{pmatrix}
z_1 \\
z_2
\end{pmatrix} = \begin{pmatrix}
\cos(a_3)\, e^{ia_1} \\
\sin(a_3)\, e^{ia_2}
\end{pmatrix}.
a_1, a_2, a_3 を使うと写像 \pi(z_1, z_2) = (2\text{Re}(z_2 \overline{z_1}), 2\text{Im}(z_2 \overline{z_1}), |z_1|^2 - |z_2|^2) は以下のようになる.
\pi(z_1, z_2) = (\sin(2a_3)\cos(a_2-a_1), \sin(2\alpha_3)\sin(a_2-a_1), \cos(2\alpha_3)).
S^2 の極座標表示を見やすくするために, \theta=2a_3, \varphi=a_2-a_1, \psi=a_1 とおく.
\begin{pmatrix}
z_1 \\
z_2
\end{pmatrix} = \begin{pmatrix}
\cos(\theta/2)\, e^{i\psi} \\
\sin(\theta/2)\, e^{i(\psi+\varphi)}
\end{pmatrix} = e^{i\psi}\begin{pmatrix}
\cos(\theta/2) \\
\sin(\theta/2)\, e^{i\varphi}
\end{pmatrix}.
e^{i\psi} はヒルベルト空間 \mathbb{C}^2 のスカラー倍を表すものであり, Hopf fibration 適用後には消えてしまうので, Hopf fibration の値に影響しない. 以上より, Hopf fibration が Bloch sphere 表示でよく見かける成分で表示される.
\pi(\cos(\theta/2), \sin(\theta/2)\, e^{i\varphi}) = (\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta).
定義域は 0 \leq \theta \leq \pi, 0 \leq \varphi < 2\pi である.
可視化
量子コンピュータでの表記に習い, \mathbb{C}^2 の基底 \Ket{0}=(1,0), \Ket{1}=(0,1) を考える. 以上をまとめると, 1 量子ビットの状態を表す
v = \cos(\theta/2)\Ket{0} + \sin(\theta/2)\, e^{i\varphi}\Ket{1}
という表記はヒルベルト空間 \mathbb{C}^2 上のベクトルを表す表記で, Bloch sphere S^2 上では Hopf fibration を通して
\pi(v) = (\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)
という点に対応していると理解できる. 以下, 代表的な状態ベクトルとその Bloch sphere 上の対応する点を表にまとめた.
| (\theta, \varphi) |
v = \cos(\theta/2)\Ket{0} + \sin(\theta/2)\, e^{i\varphi}\Ket{1} |
\pi(v) = (\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta) |
| (0, 0) |
\Ket{0} |
(0,0,1) |
| (\pi, 0) |
\Ket{1} |
(0,0,-1) |
| (\pi/2, 0) |
(\Ket{0}+\Ket{1})/\sqrt{2} |
(1,0,0) |
| (\pi/2, \pi/2) |
(\Ket{0}+i\Ket{1})/\sqrt{2} |
(0,1,0) |
パラメータ \theta, \varphi の変化の様子を qiskit の plot_bloch_vector で可視化した様子を示す.
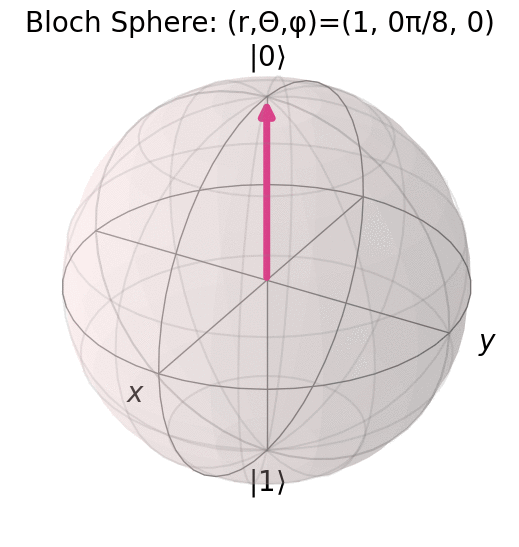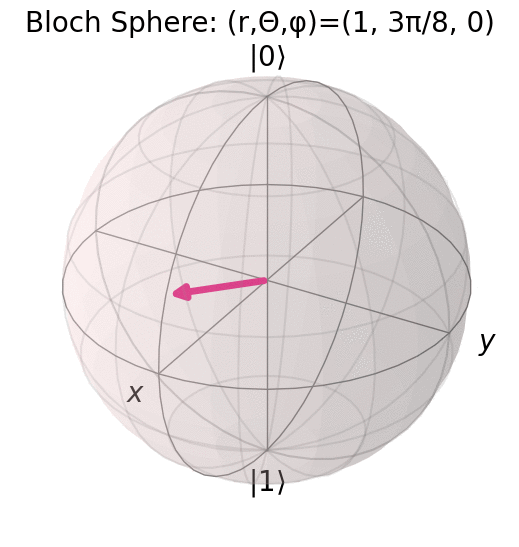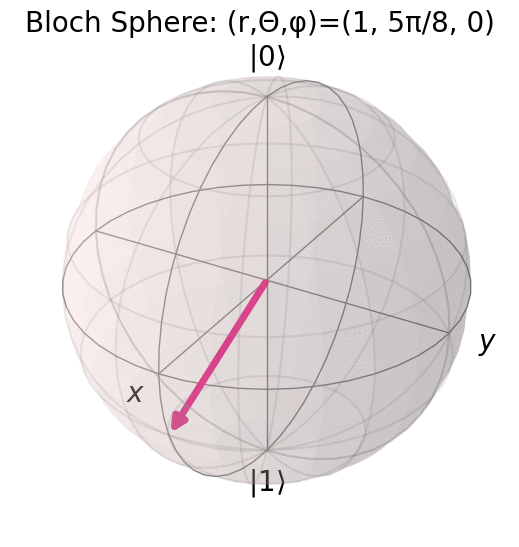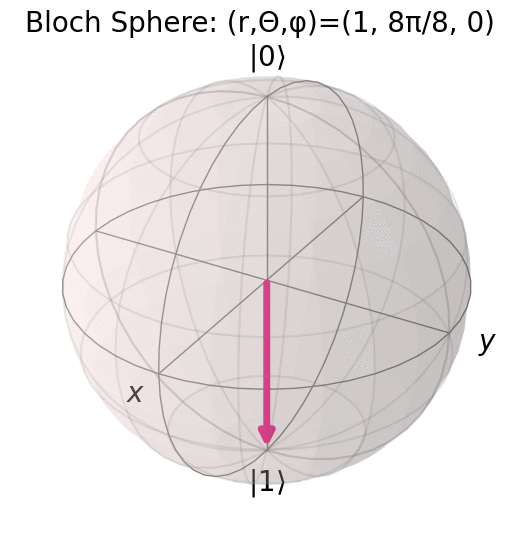
\Ket{0} に対応する点から \varphi=0 として \theta を \pi/8 ずつ \pi まで変化させた様子
(\Ket{0}+\Ket{1})/\sqrt{2} に対応する点から \varphi を \pi/4 ずつ変化させた様子
立体射影による対応
これまで射影演算子の行列を単位行列とパウリ行列 \sigma_1, \sigma_2, \sigma_3 を使って表すことで Hopf fibration の S^2 上での成分を計算していたが, この節では S^2 の立体射影を使った計算方法を紹介する.
射影演算子を使った時と同様に (z_1, z_2) \in S^3 を極座標表示する.
\begin{pmatrix}
z_1 \\
z_2
\end{pmatrix} = \begin{pmatrix}
\cos(\theta/2)\, e^{i\psi} \\
\sin(\theta/2)\, e^{i(\psi + \varphi)}
\end{pmatrix}.
ここで z_2 \neq 0 を仮定し, S^3 \subset \mathbb{C}^2 上の複素数スカラー倍の影響を除くような以下の写像 q:S^3-\{(z_1, z_2) \in S^3 \:|\: z_2 \neq 0 \} \longrightarrow \mathbb{C} を考える. この写像 q は z_2 \neq 0 に対する Hopf fibration f(z_1, z_2) = [(z_1, z_2)] を複素数平面 \mathbb{C} で座標表示 (非斉次座標) したものである.
q(z_1, z_2):= \frac{z_1}{z_2} = \frac{\cos(\theta/2)}{\sin(\theta/2)}e^{i\varphi}.
\mathbb{C} を 3 次元空間 \mathbb{R}^3 の xy-平面と同一視して, q(z_1, z_2) = (x, y, 0) と置き, 以下のように S^2 の北極点 (0,0,1) と (x, y, 0) を結ぶ線分と S^2 の交点 p(x,y,0) を求める.
(1-t)(0,0,1) + t(x,y,0) \in S^2
を満たす実数 t \in (0,1) は
t=\frac{2}{x^2 + y^2 + 1}
だけなので,
p(x,y,0) = \left(\frac{2x}{x^2 + y^2 + 1}, \:\frac{2y}{x^2 + y^2 + 1}, \:1 - \frac{2}{x^2 + y^2 + 1}\right).
写像 p を元の極座標表示で表すと,
p\left(\frac{\cos(\theta/2)}{\sin(\theta/2)}e^{i\varphi}\right)
=(\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)
となる. この写像 p:\mathbb{C} \longrightarrow S^2 -\{ (0,0,1) \} の逆写像を北極点からの立体射影という. この写像 p, q を使い,
\pi(z_1, z_2):=
\begin{cases}
\quad p\circ q(z_1, z_2) & (z_2\neq0), \\
\quad (0,0,1) & (z_2=0)
\end{cases}
と写像 \pi:S^3 \longrightarrow S^2を定め, 極座標表示をすると, 以下が得られる.
\pi(\cos(\theta/2), \sin(\theta/2)\, e^{i\varphi}) = (\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta).
射影演算子による計算の時と同様にパラメータ \psi は写像 q の適用によって消えてしまう. 以上より, 立体射影を使って射影演算子による Hopf fibration の表示と同じ表示を得ることができた.
まとめ
量子コンピュータの理論に現れる 1 量子ビットでの Bloch sphere 表示は Hopf fibration f:S^3 \longrightarrow \mathbb{C}P^1 を射影演算子あるいは立体射影を使って S^2 上で表示したものであることを成分計算で確かめた.


Discussion