Zenn
👨‍🔬

VR研究者ネットワークの分析をやってみた

2022/02/24に公開
Python
VR
idea

概要

すごく忙しい人向けの概要

  • 近年VRが発展しているけれどもその研究の発展の仕方はよくわかっていないよ！
  • 調べてみたら他の研究分野と同じく、研究者の人数の割に世界は狭そう。
  • 研究を引っ張っている人を探して、その結果は従来の方法と比較して正しそうだった。

真面目な概要

近年、バーチャルリアリティ技術の発展が著しく, 新たな産業が勃興している.
バーチャルリアリティはを牽引する技術開発は様々な分野に及び, その研究の発展の関係性は調査が不十分である.そこで筆者は研究者のネットワークに注目してネットワークバーチャルリアリティに関連する論文から研究者の共著関係のネットワークを構築した. そして, そのネットワークを分析することでバーチャルリアリティの研究者のネットワークはスケールフリーネットワークに近く, スモールワールド性を持ちうることが示唆された. 共著ネットワーク分析から研究のキープレイヤーとなっている研究者を特定して, その結果を既存の結果と比較して妥当性を確認した.

背景

近年, バーチャルリアリティ(VR)の技術が発展してきてバーチャル空間を提供するサービスが勃興し, その関連産業も成長している. VRの今後を占う上で研究開発が重要なのは言うまでもない. その研究の発展のメカニズムを知ることは政府や企業の研究開発の資金配分や研究者の研究戦略に役立つと考えられる.
研究のメカニズムを調べる方法と研究者の共著関係を調べることが古くから行われている.
古くから知られているものに数学者のポール・エルデシュとの近さを示すエルデシュ数がある[1].
近年ではデータ解析によって共著関係のネットワークを調べてパターンを研究することが行われている[2][3]. 共著関係を含む様々な社会的ネットワークや代謝ネットワークやインターネットがスケールフリー性やスモールワールド性を持つことが知られている[4].
VR分野の研究は先行研究[5]があるものの, 分析対象となったデータが論文約1200件とネットワークの規模が小さいためより包括的な調査が求められる. なぜならばVRの研究は基礎研究のみならず, その応用が多岐に渡るからである.
そこで今回はVRに関連する論文でより多くの論文を元に共著関係を分析する.

データと手法

データは Elsevier 社の提供するScopusを用いて入手し, 分析対象とする. タイトル, キーワード, アブストラクトにvirtualとrealityをそれぞれ含むものとした. 検索の結果, 論文数が151,147件の文献があった. このままではデータ数が多すぎて解析が困難であったため, 被引用数で上位10%に入っている論文15,114件を解析対象とした. Scopusで割り振られた著者IDを著者の識別に用いる.
ネットワークの構築は Newman [3]と同じ手法をとる. 著者をノード, 共著関係をリンクとする. 共著関係は研究者どうしの親しさを表すが, 10 人で共著の論文を書く関係よりも 2 人で共著の論文を書く関係のほうがより親しいと考えられる.
著者 A,B の二人が N 本の論文で共著になっているとする. このとき, 誰が研究を主体的に勧めたのかわからないので無向グラフとする. N 本の論文の著者数がそれぞれ n_i\quad (i = 1,\ldots , N ) であるとする. このとき二人の間のリンクの重みを\sum_{i=1}^N1/(n_i-1) と定義する.

分析には Python でコードを実装し, graph_tool[6]ライブラリを用いて分析を行った.

結果と考察

構築したネットワークはノード数が54,630, リンク数が191,598であった. ネットワークの全体を力学モデルで可視化した結果をここに示す.
ネットワーク全体であると非連結であった. 最大連結成分はノード数21,197, リンク数105,539である. 最大の連結成分も同様に力学モデルを用いてここに可視化した結果を示す.

ネットワーク全体の可視化

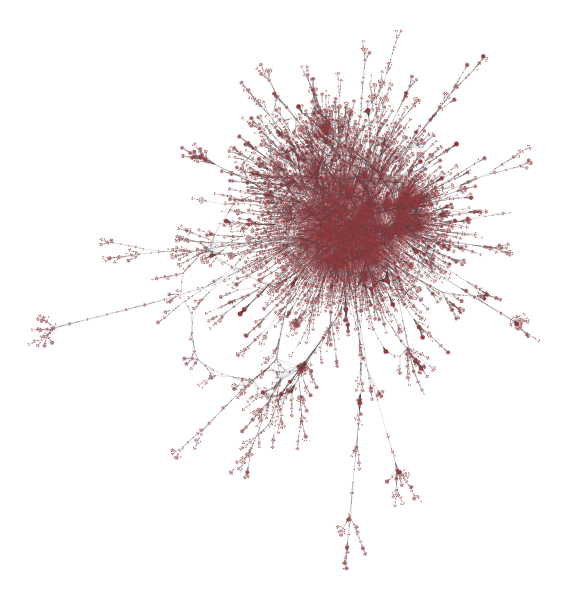
最大連結成分の可視化

スモールワールド性

このネットワークのスモールワールド性を議論する.
スモールワールド性を以下の3つの性質と定義する.

  • 全リンク数が全ノード数の数倍程度
  • 平均ノード間距離がノード数にくらべて小さい
  • 高度にクラスター化している
    これらの指標としてリンク数とノード数の比, 平均経路長, クラスタ係数の3つを用いる.
    平均経路長は経路長の平均値である. クラスター係数はWatts and Strogatz[7]の定義を用いる.
    それぞれのノードのクラスター係数は以下の通りである.
\begin{aligned} C_i = \frac{\mathrm{the\,number\,of\,connected\,triangles}}{\frac{k_i(k_i -1)}{2}} \end{aligned}

0\leq C_i\leq 1となり, ノードiに凝集しているか否かの指標となる.
ネットワーク全体のクラスター係数は全てのクラスター係数の平均値として定義する.

\begin{aligned} C = \frac{1}{N}\sum_i C_i \end{aligned}

ここでNはネットワークのノード数である. 以上の指標をネットワーク全体と最大の連結成分に対してそれぞれ計算した. 計算結果を以下の表に示す.

ネットワーク リンク数とノード数の比 平均経路長 クラスタ係数
ネットワーク全体 3.51 (非連結のため未定義) 0.838
最大の連結成分 4.98 3.304 0.843

ネットワーク全体は非連結であり, スモールワールド性の性質2.を議論することができないため, スモールワールド性を持つか判断はできない. しかしながら, 他の性質がスモールワールド性の条件を満たしている. さらに最大連結成分で平均経路長を計算するとノード数が21,197もあるのにもかかわらず平均経路長が3.304と平均ノード間距離がノード数にくらべて大変小さい.
ネットワークの構築に用いた論文が限られているので最大連結成分が既存の研究と比べて小さいが[3], 被引用ネットワーク全体もスモールワールドであることがある程度示唆される.

次数分布

次数分布がべき乗則に従っているネットワークはスケールフリーネットワークと呼ばれる. ここで, このネットワークがスケールフリーであるかどうかを次数分布をプロットして調べる.
べき分布とは

\begin{aligned} p(k) = {\alpha}{k^{\gamma}} \end{aligned}

となる分布で\alpha,\gammaは定数である. べき分布は独立変数kのスケールを変化させても関数自体のスケーリングとなる性質をもつ. kをc倍にスケーリングした場合

\begin{aligned} p(ck) = \frac{\alpha}{(ck)^{\gamma}} =\frac{\alpha}{c^{\gamma}k^{\gamma}} = \frac{1}{c^{\gamma}}p(k) \end{aligned}

となり, スケーリングに対してその特徴が変化しない. 次数分布がスケールフリー性をもつ場合,
ネットワークが自己相似性をもつことが指摘されている[8].
次数分布のヒストグラムを作成し, スケールフリーネットワークのべき乗則に従っているかどうかを調べる. ネットワーク全体と最大連結成分に対してそれぞれべき分布へのフィッティングを行い, べき指数の推定とR^{2} 値を求めた. べき指数\gammaの推定結果を以下の表に示す.

ネットワーク \gamma {R^{2}}
ネットワーク全体 2.29 0.827
最大連結成分 2.03 0.800
最大連結成分を除いたもの 2.71 0.807

以下の図にヒストグラムとフィッティングした結果の直線を示す.

次数分布　(左:全体, 中央:最大連結成分, 右:最大連結成分を除いたのもの)

左図が全体の次数分布, 中央図が最大連結成分の次数分布, 右図が最大連結成分を除いたのものの次数分布である. 表より相関係数はすべてにおいて0.8以上となり, それぞれスケールフリーネットワークであると考えられる.

次数が小さい領域と大きい領域において回帰曲線からの差が大きい. 次数が多いノードの頻度が近似曲線よりも大きいことは, 一部の著者が多くの共著関係を持っていることを示している. その理由として, 活発な研究者により多くの共同研究が申し込まれることが考えられる. 次数が小さいノードの数が冪乗則よりも少ないのは, 引用件数で上位10%と論文を区切ったことによる偏りと考えられる. その例として, 活発でない研究者は引用数の上位10%に到達する論文を書いておらず, データから除外されているからであると考えられる.

ノード中心性

ノード中心性を調べ, 研究において中心的な役割を果たしている研究者を特定する. 中心性の指標としてPageRankを用いる. Pagerankを採用した理由はネットワークが非連結であっても中心性を適切に求めることができるからである(詳細はこちら).
PageRankはネットワークの隣接行列の固有ベクトル中心性と似ているが, 固有ベクトル中心性と異なり, 全てのネットワークが連結されるようにネットワークを修正する手法である. 以下, PageRankの計算アルゴリズムをマルコフ連鎖と解釈して概説する. まず, ネットワークの隣接行列\bm{A}から確率遷移行列\bm{T}を求める.

\begin{aligned} \bm{T} = \{T_{nm}\} \end{aligned}

ここでノードmから遷移することができないノードをダングリングノードという. ダングリングノードに対してネットワークを連結になるように修正を行う.

\begin{aligned} \bm{M} = (1-\rho)\bm{T}+ \rho\bm{B},\quad B=\frac{1}{N} \begin{bmatrix} 1 &\ldots & 1 \\ \vdots & \ddots & \vdots \\ 1 &\ldots & 1 \end{bmatrix} \end{aligned}

ここで\rhoはダンピング係数と呼ばれ, \rho=0.15とした. ノードiのPageRankをp_iとし, 全てのノードのPageRankを束ねたベクトルを\bm{p}と表記する. 修正した遷移行列に対してページランクのベクトル\bm{p}^{(n)}を収束するまで以下の計算を繰り返す.

\begin{aligned} \bm{p}^{(n+1)} = \bm{M}\bm{p}^{(n)} \end{aligned}

PageRankを計算し, 結果を可視化したものを以下の図に示す. 上位の研究者はネットワークの中心に位置しており, 力学アルゴリズムで中心に来るネットワークとの関連があると考えられる.

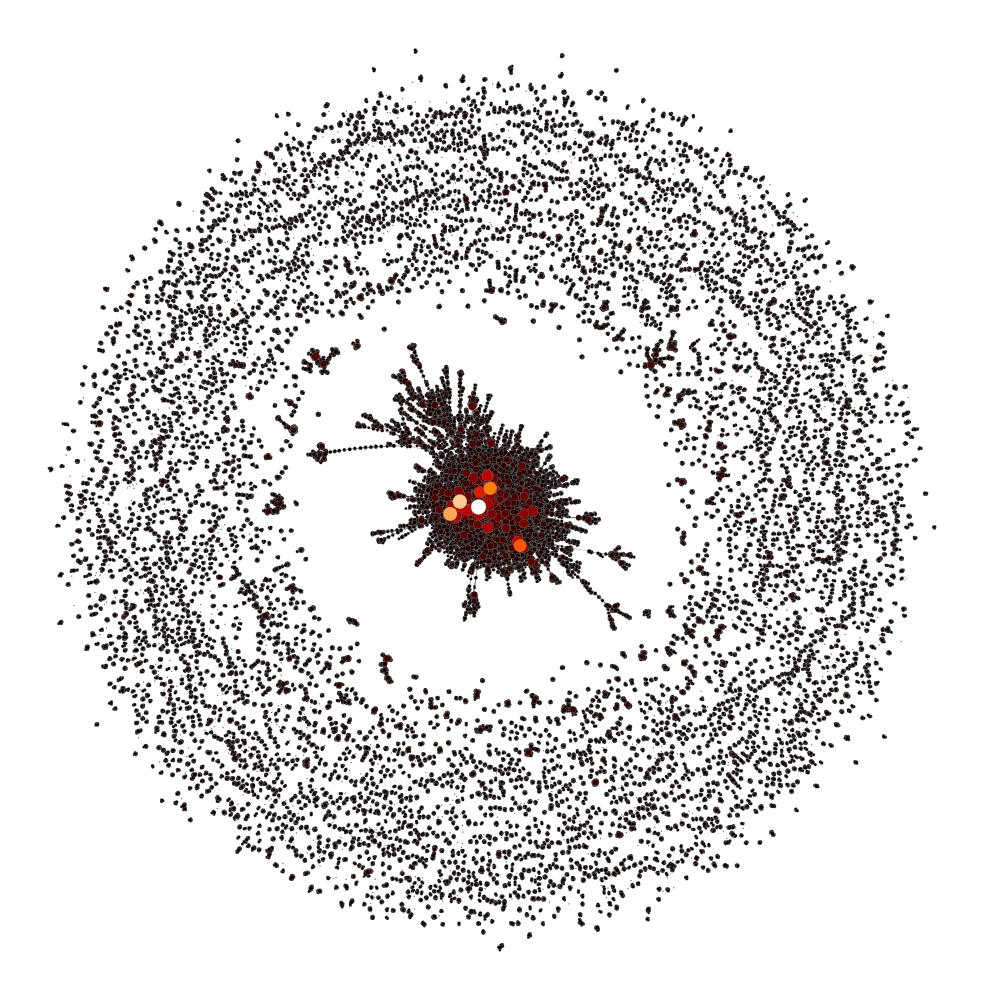
PageRankの上位10人をScopus IDから著者名を入手し, 以下の表に示す. PageRank1位のSlater, M.氏はIEEE VGTC Virtual Reality Career Award 2005を受賞しており, h-indexが70とすぐれた研究者である. 2位のRizzo, A.氏はh-indexが56と著名な研究者である. このように, 活発に活動していて, その成果が顕著な研究者を抽出出来ている. よってPageRankを用いることで共著ネットワークから, 活発に活動していてその成果が著名な研究者の抽出が可能であると考えられる.

Scopus 著者ID PageRank 著者名 h-index
7202932472 0.0006561279784914033 Slater, M. 70
57189943380 0.0005855456596639115 Rizzo, A. 56
56962750600 0.0005436732072967205 Riva, G. 62
7006142663 0.0004943600285748912 Billinghurst, M. 53
14633357600 0.00043743650102115363 Darzi, A. 108
55101019100 0.00036847517888017743 Schmalstieg, D. 49
8616911800 0.0003241443204149316 Aggarwal, R. 57
7201677607 0.0003231734771980218 Hoffman, H. 46
7005885082 0.00032233736374220136 Thalmann, D. 54
57203070046 0.00030762284697978103 Rothbaum, B.O. 75

結論

VR研究の引用件数上位10%の論文の著者の共著関係のネットワークを構築して分析した. 共著関係のネットワークは非連結であるものの, スモールワールド性が示唆された. 次数分布を求めると, データの偏りによる著者の偏りが存在しうるが, 自己相似性が示唆される上にべき乗則に従っており, スケールフリーネットワークであると考えられる. PageRankを用いて研究で中心的な役割を担っている研究者を抽出し, その結果が妥当であることを確認できた.

今回はScopusの仕様や計算時間により断念せざるを得なかったが, データを全ての論文を対象にネットワークを構築したり, クラスタリングを行ってコミュニテイについて考察したり, ネットワークの時系列の変化も調査したりすることを今後の課題とする.

謝辞

アイデアの発案といくつかの洞察, そして文章の改善案を頂いたKuroly氏に謝意を示す.

参考文献

  1. C. Goffman, “And what is your erdos number?” The American Mathematical Monthly, vol. 76, no. 7, pp. 791–791, 1969.
  2. M. E. J. Newman, “The structure of scientific collaboration networks,” Proceedings of the National Academy of Sciences, vol. 98, no. 2, pp. 404–409, 2001.
  3. M. E. J. Newman, “Coauthorship networks and patterns of scientific collaboration,” Proceedings of the National Academy of Sciences, vol. 101, no. suppl 1, pp. 5200–5205, 2004.
  4. “The structure and function of complex networks,” SIAM Rev. Soc. Ind. Appl. Math., vol. 45, no. 2, pp. 167–256, Jan. 2003.
  5. M.-D. González-Zamar and E. Abad-Segura, “Implications of virtual reality in arts education: Research analysis in the context of higher education,” Education Sciences, vol. 10, no. 9, 2020.
  6. T. P. Peixoto, “The graph-tool python library,” figshare, 2014.
  7. D. J. Watts and S. H. Strogatz, “Collective dynamics of ’small-world’ networks,” Nature, vol. 393, no. 6684, pp. 440–442, 1998.
  8. C. Song, S. Havlin, and H. A. Makse, “Self-similarity of complex networks,” Nature, vol. 433, no. 7024, pp. 392–395, Jan. 2005.
  9. L. Page, S. Brin, R. Motwani, and T. Winograd, “The pagerank citation ranking: Bringing order to the web.,” Stanford InfoLab, Tech. Rep., 1999.

Discussion