📖

マルコフ決定過程：強化学習コース(2/N)

2025/06/29に公開

はじめに

前回の記事では、強化学習の基本的な問題設定について、環境側とエージェント側の定義を区別して説明しました。本記事では、その知識を踏まえて、強化学習の基礎となるマルコフ決定過程（Markov Decision Process; MDP） について詳しく解説します。

内部状態が完全に観測可能な場合

前回の記事では、現実の多くの問題で環境の内部状態を直接観測できない「観測可能性とノイズ」の問題について触れました。しかし、多くの強化学習の解説や初学者向けの問題設定では、この複雑さを避けるため、内部状態がそのまま観測できるという仮定を置きます。

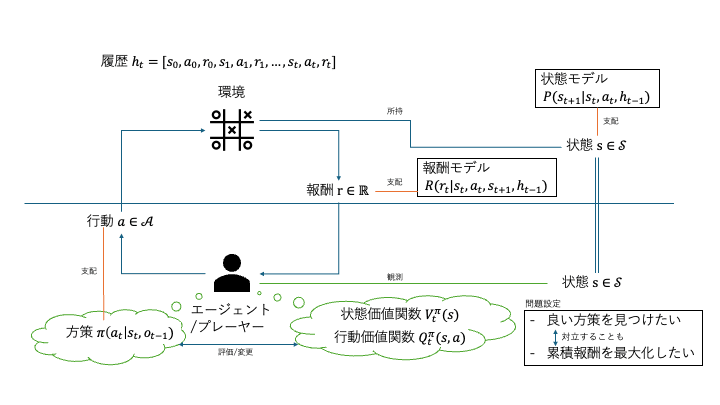
マルコフ決定過程の設定

この図は、内部状態 $s \in \mathcal{S}$ がエージェントによって直接観測される状況を示しています。この設定では、観測 $\tilde{s} = s$ となり、エージェントは環境の真の状態を完全に把握できます。

マルコフ決定過程の定義

内部状態が完全に観測可能という仮定の下では、強化学習の問題はマルコフ決定過程として定式化されます。

マルコフ性の導入

マルコフ決定過程の核心となるのはマルコフ性です。これは、次の状態と報酬が現在の状態と行動にのみ依存し、過去の履歴には依存しないという性質です。

この性質により、エージェントは過去の長い履歴を記憶する必要がなく、現在の状態と行動のみから意思決定を行うことができます。

MDPの構成要素

マルコフ決定過程は以下の4つの要素で定義されます：

$\text{MDP} = \langle \mathcal{S}, \mathcal{A}, P, R \rangle$

$\mathcal{S}$ : 状態集合（State Space）
$\mathcal{A}$ : 行動集合（Action Space）
$P$ : 状態遷移確率関数 $P: \mathcal{S} \times \mathcal{A} \to \mathcal{P}(\mathcal{S})$
$R$ : 報酬関数 $R: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \to \mathcal{P}(\mathbb{R})$

状態遷移確率関数

状態遷移確率関数 $P(s'|s,a)$ は、状態 $s$ で行動 $a$ を取ったときに次の状態 $s'$ に遷移する確率を表します。この関数は2つの重要な性質を持ちます：

マルコフ性: この確率は過去の履歴に依存せず、現在の状態と行動のみで決まります。
時不変性（定常性）: 任意の時刻 $t, t'$ に対して、
$P(S_{t+1}=s'|S_t=s, A_t=a) = P(S_{t'+1}=s'|S_{t'}=s, A_{t'}=a) = P(s'|s,a)$
が成り立ちます。つまり、環境の遷移規則は時間によって変化せず、一つの条件付き確率 $P(s'|s,a)$ で表現できます。

これらの性質により、エージェントは一度学習した環境のダイナミクスを将来にわたって活用できます。

報酬関数

報酬関数 $R(r|s,a,s')$ は、状態 $s$ で行動 $a$ を取って状態 $s'$ に遷移したときに報酬 $r$ を得る確率分布を表します。報酬関数も状態遷移関数と同様に時不変性を持ちます：

任意の時刻 $t, t'$ に対して、

P(R_t=r|S_t=s, A_t=a, S_{t+1}=s') = P(R_{t'}=r|S_{t'}=s, A_{t'}=a, S_{t'+1}=s') = R(r|s,a,s')

実際の問題では、期待報酬 $\mathbb{E}[R|s,a,s']$ として扱われることも多くあります。なお、報酬が次の状態のみに依存する場合（ $R(s') = R(r|s')$ ）や、状態と行動のペアのみに依存する場合（ $R(s,a) = R(r|s,a)$ ）として簡略化されることもあります。

Pythonでマルコフ決定過程を体験する

マルコフ決定過程の概念を理解するために、実際のPythonコードを通じて環境とエージェントの相互作用を実装してみましょう。まず、型安全で拡張可能な強化学習環境の設計思想から説明します。

型安全な環境設計

強化学習では、環境とエージェントの相互作用を統一的なインターフェースで表現することが重要です。以下のコードは、Generic型を活用して型安全性を確保し、どの理論的枠組み（MDP、POMDP、マルチエージェントなど）でも利用可能な汎用的な環境インターフェースを定義しています：

型定義

from typing import Any, Dict, Generic, TypeVar, Protocol
from pydantic import BaseModel, Field

# 型変数の定義
StateType = TypeVar('StateType')  # 環境の内部状態
ActionType = TypeVar('ActionType')  # 行動
ObservationType = TypeVar('ObservationType')  # 観測 = NoisedState


class StateTransition(BaseModel, Generic[StateType, ActionType]):
    """
    環境内部での状態遷移エントリ
    
    環境が内部的に管理する状態遷移の記録。観測の記録はエージェント側の責務。
    """
    previous_state: StateType = Field(description="遷移前の内部状態")
    action: ActionType = Field(description="実行された行動")
    next_state: StateType = Field(description="遷移後の内部状態")
    reward: float = Field(description="受け取った報酬")
    done: bool = Field(description="エピソード終了フラグ")
    info: Dict[str, Any] = Field(default_factory=dict, description="追加情報")

    class Config:
        arbitrary_types_allowed = True


class NoiseChannel(Protocol, Generic[StateType, ObservationType]):
    """
    ノイズチャネルのプロトコル
    
    状態から観測への条件付き確率 P(O|S) を実装する。
    NoisedState = Observation として、環境はこのチャネルを通したObservationを返す。
    """
    
    def sample_observation(self, state: StateType) -> ObservationType:
        """
        与えられた状態から観測をサンプリングする
        
        Args:
            state: 現在の内部状態
            
        Returns:
            サンプリングされた観測（NoisedState）
        """
        ...
    
    def get_observation_probability(self, observation: ObservationType, state: StateType) -> float:
        """
        P(O|S) の確率を返す
        
        Args:
            observation: 観測
            state: 状態
            
        Returns:
            条件付き確率 P(observation|state)
        """
        ...

汎用環境基底クラス

from abc import ABC, abstractmethod
from typing import Any, Dict, List, Optional, Generic, TypeVar


class Environment(ABC, Generic[StateType, ActionType, ObservationType]):
    """
    強化学習環境の抽象基底クラス
    
    エージェントと環境の相互作用を定義する最小限のインターフェース。
    どの理論的枠組み（MDP、POMDP、マルチエージェントなど）でも利用可能。
    """
    
    def __init__(self, noise_channel: Optional[NoiseChannel[StateType, ObservationType]] = None):
        """
        環境を初期化する
        
        Args:
            noise_channel: ノイズチャネル P(O|S) （dependency injection）
        """
        self._history: List[StateTransition[StateType, ActionType]] = []
        self._current_state: Optional[StateType] = None
        self._current_observation: Optional[ObservationType] = None
        self._episode_done: bool = False
        self._noise_channel = noise_channel
        self._seed: Optional[int] = None
    
    @abstractmethod
    def internal_reset(self, **kwargs) -> StateType:
        """
        環境の内部状態をリセットして初期状態を返す
        
        Args:
            **kwargs: 環境固有のリセット引数
            
        Returns:
            初期内部状態
        """
        pass
    
    def reset(self, **kwargs) -> ObservationType:
        """
        環境をリセットして初期観測を返す
        
        Args:
            **kwargs: 環境固有のリセット引数
            
        Returns:
            初期観測（NoisedState）
        """
        self._reset_history()
        
        # 内部状態をリセット
        initial_state = self.internal_reset(**kwargs)
        self._current_state = initial_state
        
        # 初期観測を生成
        initial_observation = self._generate_observation(initial_state)
        self._current_observation = initial_observation
        
        return initial_observation
    
    @abstractmethod
    def internal_step(self, action: ActionType) -> tuple[StateType, float, bool, Dict[str, Any]]:
        """
        環境内部での純粋な状態遷移を実行する
        
        このメソッドは環境内部での制御を行う：
        1. 行動を受け取り状態遷移を実行
        2. 報酬を計算
        3. 履歴への記録はしない（stepメソッドで行う）
        
        Args:
            action: 実行する行動
            
        Returns:
            next_state: 次の内部状態
            reward: 受け取った報酬
            done: エピソード終了フラグ
            info: 追加情報
        """
        pass
    
    def step(self, action: ActionType) -> tuple[ObservationType, float, bool, Dict[str, Any]]:
        """
        行動を実行して観測を返す（プレイヤー側インターフェース）
        
        このメソッドは以下の手順で動作する：
        1. internal_stepで状態遷移を実行
        2. ノイズチャネルで状態から観測を生成
        3. 履歴に記録
        
        Args:
            action: 実行する行動
            
        Returns:
            observation: 次の観測（NoisedState）
            reward: 受け取った報酬
            done: エピソード終了フラグ
            info: 追加情報
        """
        # 初期化チェック
        if self._current_state is None:
            raise RuntimeError(
                "step() called before reset(). "
                "You must call reset() before the first step()."
            )
        
        previous_state = self._current_state
        
        # 1. 環境内部での状態遷移を実行
        next_state, reward, done, info = self.internal_step(action)
        
        # 2. 観測を生成（各ステップで新規生成）
        observation = self._generate_observation(next_state)
        self._current_observation = observation
        
        # 3. 履歴に記録
        self._add_state_transition(
            previous_state=previous_state,
            action=action,
            next_state=next_state,
            reward=reward,
            done=done,
            info=info
        )
        
        return observation, reward, done, info
    
    @abstractmethod
    def get_action_space(self) -> List[ActionType]:
        """
        利用可能な行動の集合を返す
        
        Returns:
            行動集合のリスト
        """
        pass
    
    def get_history(self) -> List[StateTransition[StateType, ActionType]]:
        """
        環境の履歴を返す
        
        Returns:
            状態遷移の履歴
        """
        return self._history.copy()
    
    def is_done(self) -> bool:
        """エピソードが終了しているかを返す"""
        return self._episode_done
    
    def get_current_state(self) -> Optional[StateType]:
        """
        現在の内部状態を返す
        
        Returns:
            現在の状態、初期化されていない場合はNone
        """
        return self._current_state
    
    # === 継承クラス用のヘルパーメソッド ===
    
    def _reset_history(self) -> None:
        """履歴をリセットする"""
        self._history = []
        self._current_state = None
        self._current_observation = None
        self._episode_done = False
    
    def _add_state_transition(self, previous_state: StateType, action: ActionType,
                             next_state: StateType, reward: float, done: bool, 
                             info: Dict[str, Any]) -> None:
        """状態遷移を履歴に追加する"""
        transition = StateTransition(
            previous_state=previous_state,
            action=action,
            next_state=next_state,
            reward=reward,
            done=done,
            info=info
        )
        self._history.append(transition)
        self._current_state = next_state
        self._episode_done = done
    
    def _generate_observation(self, state: StateType) -> ObservationType:
        """
        状態から観測を生成する
        
        Args:
            state: 内部状態
            
        Returns:
            生成された観測
        """
        if self._noise_channel is None:
            raise RuntimeError(
                "NoiseChannel is not set. "
                "You must provide a NoiseChannel when initializing the environment "
                "to generate observations from states."
            )
        
        observation = self._noise_channel.sample_observation(state)
        return observation

環境設計の特徴

この環境設計では、以下の特徴を持つ実装を採用しています：

1. Generic型による型安全性の実現

class Environment(ABC, Generic[StateType, ActionType, ObservationType]):

この宣言により、環境を作成する際に状態・行動・観測の型を明示的に指定できます。例えば：

# グリッドワールドの場合
GridWorldEnvironment(Environment[Tuple[int, int], str, Tuple[int, int]])
# 状態: (x, y)座標、行動: "up"/"down"等の文字列、観測: (x, y)座標

これにより、IDEでの補完や型チェックが効くようになり、開発時にバグを早期発見できます。

2. 責務の明確な分離

従来のstep()メソッドが行っていた複数の処理を分離しました：

internal_step(): 環境固有のロジックのみを担当

def internal_step(self, action: str) -> tuple[StateType, float, bool, Dict[str, Any]]:
    # 純粋な状態遷移のみ - 履歴管理や観測生成は行わない
    next_state = self._sample_next_state(current_state, action)
    reward = self.reward_model(current_state, action, next_state)
    return next_state, reward, done, info

step(): 基底クラスが共通処理を自動実行

def step(self, action: ActionType) -> tuple[ObservationType, float, bool, Dict[str, Any]]:
    # 1. 環境固有の状態遷移を実行
    next_state, reward, done, info = self.internal_step(action)
    # 2. 観測を生成
    observation = self._generate_observation(next_state)
    # 3. 履歴に記録
    self._add_state_transition(...)
    return observation, reward, done, info

この分離により、環境の実装者は純粋なMDPロジックのみに集中でき、履歴管理や観測生成は基底クラスが自動処理します。

3. Dependency Injectionによる観測モデルの分離

従来は環境クラス内に観測生成ロジックが埋め込まれていましたが、NoiseChannelプロトコルにより外部から注入できるようになりました：

# 決定的観測（状態 = 観測）
class DeterministicChannel(NoiseChannel):
    def sample_observation(self, state):
        return state  # 状態をそのまま返す

# ノイズ付き観測（将来の拡張例）
class NoisyChannel(NoiseChannel):
    def sample_observation(self, state):
        return state + np.random.normal(0, 0.1)  # ガウシアンノイズを追加

# 環境作成時に観測モデルを選択
env = GridWorldEnvironment(noise_channel=DeterministicChannel())

これにより、同じ環境で異なる観測条件を実験でき、POMDPへの拡張も容易になります。

4. Pydanticによるデータ構造の型安全性

履歴データの構造を型安全に定義：

class StateTransition(BaseModel, Generic[StateType, ActionType]):
    previous_state: StateType
    action: ActionType
    next_state: StateType
    reward: float
    done: bool
    info: Dict[str, Any]

これにより、履歴データへのアクセスが型安全になり、IDEでの補完も効きます：

history = env.get_history()
first_transition = history[0]
print(first_transition.action)  # 型チェックされ、補完も効く
print(first_transition.reward)  # floatであることが保証される

マルコフ決定過程の実装

上記のインターフェースを使って、実際のグリッドワールド環境を実装してみましょう。この実装では、MDPの4つの構成要素 $\langle \mathcal{S}, \mathcal{A}, P, R \rangle$ を完全に定義し、マルコフ性と時不変性を満たす環境を構築します。

決定的ノイズチャネルの実装

まず、グリッドワールド用の決定的なノイズチャネルを定義します。これは「状態を完全に観測できる」という仮定を実装しています：

class DeterministicGridWorldChannel(NoiseChannel[Tuple[int, int], Tuple[int, int]]):
    """決定的なグリッドワールド用ノイズチャネル"""
    
    def sample_observation(self, state: Tuple[int, int]) -> Tuple[int, int]:
        """状態をそのまま観測として返す"""
        return state
    
    def get_observation_probability(self, observation: Tuple[int, int], state: Tuple[int, int]) -> float:
        """決定的なので、状態と観測が一致する場合のみ1.0"""
        return 1.0 if observation == state else 0.0

実装のポイント:

NoiseChannel[Tuple[int, int], Tuple[int, int]]で、状態と観測が同じ型（座標）であることを明示
sample_observation()では状態をそのまま返すことで「完全観測」を実現
get_observation_probability()では、状態と観測が一致する場合のみ確率1.0を返す（決定的観測）

この設計により、将来的にノイズ付き観測や部分観測への拡張が容易になります。

グリッドワールド環境の実装

ここからは、上記の設計を実际に使ってグリッドワールド環境を実装していきます。この実装では、MDPの数学的定義を忠実に再現し、マルコフ性と時不変性を保証します。

import numpy as np
from typing import Tuple, Dict, List, Optional, Any, override


class GridWorldEnvironment(Environment[Tuple[int, int], str, Tuple[int, int]]):
    """
    グリッドワールド環境
    
    N×Nのグリッド上でエージェントが移動し、ゴールを目指す環境。
    マルコフ決定過程として完全に定式化されている。
    
    MDP構成要素:
    - S: グリッド上の座標 (i, j) の集合
    - A: {"up", "right", "down", "left"} の行動集合
    - P: 状態遷移確率（決定的または確率的）
    - R: 報酬関数（ゴール到達で正の報酬、移動で負のコスト）
    """
    
    def __init__(
        self,
        size: int = 3,
        goal: Tuple[int, int] = (2, 2),
        start: Optional[Tuple[int, int]] = None,
        stochastic: bool = False,
        move_cost: float = -0.1,
        goal_reward: float = 1.0,
        random_seed: Optional[int] = None
    ):
        """
        グリッドワールドを初期化
        
        Args:
            size: グリッドのサイズ (size × size)
            goal: ゴール位置の座標
            start: 開始位置（Noneの場合は(0,0)）
            stochastic: 確率的遷移を使用するか
            move_cost: 移動時のコスト（負の値）
            goal_reward: ゴール到達時の報酬
            random_seed: 乱数シード
        """
        # 決定的なノイズチャネルを使用
        super().__init__(noise_channel=DeterministicGridWorldChannel())
        
        # 環境パラメータの保存
        self.size = size
        self.goal = goal
        self.start = start if start is not None else (0, 0)
        self.stochastic = stochastic
        self.move_cost = move_cost
        self.goal_reward = goal_reward
        
        if random_seed is not None:
            np.random.seed(random_seed)
        
        # === MDP構成要素の構築 ===
        
        # 状態集合 S: 有限集合として明示的に定義
        self._state_space = [(i, j) for i in range(size) for j in range(size)]
        
        # 行動集合 A: 4方向の移動を定義
        self._action_space = ["up", "right", "down", "left"]
        # 各行動に対応する座標変化量
        self._action_effects = {
            "up": (-1, 0),     # 上方向（y座標減少）
            "right": (0, 1),   # 右方向（x座標増加）
            "down": (1, 0),    # 下方向（y座標増加）
            "left": (0, -1)    # 左方向（x座標減少）
        }
        
        # 現在のエージェント位置（内部状態）
        self._current_position: Optional[Tuple[int, int]] = None
    
    def _build_transition_model(self) -> Dict[Tuple[int, int], Dict[str, Dict[Tuple[int, int], float]]]:
        """
        状態遷移確率関数 P(s'|s,a) を構築
        
        Returns:
            遷移確率の辞書構造
            {state: {action: {next_state: probability}}}
        """
        transitions = {}
        
        for state in self._state_space:
            transitions[state] = {}
            for action in self._action_space:
                transitions[state][action] = {}
                
                if self.stochastic:
                    # 確率的遷移：意図した方向に80%、他の方向に各5%
                    intended_next = self._get_next_state(state, action)
                    transitions[state][action][intended_next] = 0.8
                    
                    for other_action in self._action_space:
                        if other_action != action:
                            other_next = self._get_next_state(state, other_action)
                            if other_next in transitions[state][action]:
                                transitions[state][action][other_next] += 0.05
                            else:
                                transitions[state][action][other_next] = 0.05
                    
                    # 確率の正規化（数値誤差を修正）
                    total_prob = sum(transitions[state][action].values())
                    for next_state in transitions[state][action]:
                        transitions[state][action][next_state] /= total_prob
                else:
                    # 決定的遷移
                    next_state = self._get_next_state(state, action)
                    transitions[state][action][next_state] = 1.0
        
        return transitions
    
    def _get_next_state(self, state: Tuple[int, int], action: str) -> Tuple[int, int]:
        """
        決定的状態遷移関数：現在の状態と行動から一意に次状態を決定
        
        この関数はMDPの状態遷移関数 P(s'|s,a) の決定的版です。
        境界処理により、グリッドの外に出ようとする行動は同じ位置に留まります。
        
        Args:
            state: 現在の状態 (i, j)
            action: 実行する行動
            
        Returns:
            次の状態 (i', j')
        """
        i, j = state
        di, dj = self._action_effects[action]  # 行動に対応する座標変化量
        
        # 境界チェック：グリッドの範囲内に制限
        new_i = max(0, min(self.size - 1, i + di))
        new_j = max(0, min(self.size - 1, j + dj))
        
        return (new_i, new_j)
    
    def reward_model(self, state: Tuple[int, int], action: str, next_state: Tuple[int, int]) -> float:
        """
        報酬関数 R(s_t, a_t, s_{t+1}): MDPの数学的定義に従った実装
        
        この関数は「現在状態」「行動」「次状態」の3つ組に基づいて
        報酬を決定します。これはMDPの正しい定義であり、
        「次の状態に到達したこと」に基づいて報酬が決まります。
        
        Args:
            state: 現在の状態 s_t (使用しないが、インターフェースの一貫性のため)
            action: 実行した行動 a_t (同上)
            next_state: 次の状態 s_{t+1} (実際の報酬決定に使用)
            
        Returns:
            報酬値: ゴール到達時は+1.0、それ以外は-0.1（移動コスト）
        """
        # ゴールに到達した場合のみ正の報酬、それ以外は移動コスト
        return self.goal_reward if next_state == self.goal else self.move_cost
    
    def _sample_next_state(self, state: Tuple[int, int], action: str) -> Tuple[int, int]:
        """
        現在の状態と行動から次の状態をサンプリング
        
        このメソッドは確率的・決定的両方の遷移に対応します。
        stochastic=Falseの場合は決定的遷移、Trueの場合は確率的遷移を実行します。
        
        Args:
            state: 現在の状態
            action: 実行する行動
            
        Returns:
            サンプリングされた次の状態
        """
        if not self.stochastic:
            # 決定的遷移：意図した方向に100%移動
            return self._get_next_state(state, action)
        
        # 確率的遷移：意図した方向80%、他の方向圅5%ずつ
        w_intended = 0.8
        w_other = 0.05
        
        # 全行動について次状態を計算し、重みを割り当て
        actions = self._action_space
        next_states = [self._get_next_state(state, a) for a in actions]
        weights = np.array([w_intended if a == action else w_other for a in actions])
        probabilities = weights / weights.sum()
        
        # インデックスをサンプリングして対応する状態を返す
        chosen_index = np.random.choice(len(next_states), p=probabilities)
        return next_states[chosen_index]
    
    # === Environment抽象メソッドの実装 ===
    
    @override
    def internal_reset(self, start_position: Optional[Tuple[int, int]] = None, **kwargs) -> Tuple[int, int]:
        """
        環境の内部状態をリセットして初期状態を返す
        
        Args:
            start_position: 開始位置（Noneの場合はデフォルト位置）
            **kwargs: その他の引数
            
        Returns:
            初期内部状態
        """
        
        if start_position is not None:
            self._current_position = start_position
        else:
            self._current_position = self.start
        
        return self._current_position
    
    @override
    def internal_step(self, action: str) -> tuple[Tuple[int, int], float, bool, Dict[str, Any]]:
        """
        環境内部での純粋な状態遷移を実行する
        
        Args:
            action: 実行する行動
            
        Returns:
            next_state: 次の内部状態
            reward: 受け取った報酬
            done: エピソード終了フラグ
            info: 追加情報
        """
        
        if action not in self._action_space:
            raise ValueError(f"無効な行動: {action}. 有効な行動: {self._action_space}")
        
        current_pos = self._current_position
        
        # 状態遷移の実行（マルコフ性と時不変性を満たす）
        next_pos = self._sample_next_state(current_pos, action)
        
        # 報酬の計算（時不変性：R(s,a,s')は時刻に依存しない）
        reward = self.reward_model(current_pos, action, next_pos)
        
        # 終了判定
        done = (next_pos == self.goal)
        
        # 状態更新
        self._current_position = next_pos
        
        # 追加情報
        info = {
            "previous_state": current_pos,
            "action": action,
            "deterministic_next": self._get_next_state(current_pos, action),
            "actual_next": next_pos,
            "is_stochastic": self.stochastic
        }
        
        return next_pos, reward, done, info
    
    @override
    def get_action_space(self) -> List[str]:
        """利用可能な行動の集合を返す"""
        return self._action_space.copy()

実装の特徴とMDP理論の実現

このグリッドワールド実装では、MDPの数学的定義を忠実に再現し、同時にモダンなPythonの機能を活用して保守性と可読性を向上させています。

MDPの数学的定義の実現

状態集合 $\mathcal{S}$ の明示的定義

self._state_space = [(i, j) for i in range(size) for j in range(size)]

有限集合として明示的に定義し、どの状態が存在するかを明確にしています。

行動集合 $\mathcal{A}$ の定義

self._action_space = ["up", "right", "down", "left"]
self._action_effects = {
    "up": (-1, 0), "right": (0, 1), "down": (1, 0), "left": (0, -1)
}

各行動とその物理的意味（座標変化）を明示的に対応付けています。

状態遷移関数 $P(s'|s,a)$ の実装

def _sample_next_state(self, state, action):
    if not self.stochastic:
        return self._get_next_state(state, action)  # 決定的遷移
    # 確率的遷移の実装...

決定的・確率的両方の遷移を統一的なインターフェースで実現しています。

報酬関数 $R(s,a,s')$ の正しい実装

def reward_model(self, state, action, next_state):
    return self.goal_reward if next_state == self.goal else self.move_cost

MDPの定義に従い、「現在状態」「行動」「次状態」の3つ組に基づいて報酬を決定しています。

マルコフ性の保証

internal_step()メソッドでの実装に注目してください：

def internal_step(self, action):
    current_pos = self._current_position
    # 次状態の決定は current_pos と action のみに依存
    next_pos = self._sample_next_state(current_pos, action)
    # 報酬も同様に現在の情報のみに依存
    reward = self.reward_model(current_pos, action, next_pos)
    # 過去の履歴は一切使用しない

この実装により、数学的に定義されたマルコフ性 $P(S_{t+1}|S_t, A_t, H_{t-1}) = P(S_{t+1}|S_t, A_t)$ が実現されています。

時不変性の保証

環境のルールが時刻に依存しないことを保証するため、以下の設計を採用しています：

関数型アプローチ: reward_model()や_get_next_state()は純粋関数として実装
状態非依存: 環境の内部状態に依存せず、引数のみから結果を決定
時刻情報の除外: 時刻 $t$ を引数として受け取らない

型安全性とコードの保守性

Generic型パラメータの活用

class GridWorldEnvironment(Environment[Tuple[int, int], str, Tuple[int, int]]):
    # 状態: (x,y)座標、行動: 文字列、観測: (x,y)座標

コンパイル時に型エラーを検出し、IDEでの補完機能を有効にします。

@overrideデコレータによる明示性

@override
def internal_step(self, action: str) -> tuple[...]:

抽象メソッドの実装であることを明示し、メソッド名のタイプミスを防ぎます。

Pydanticによるデータ構造の検証

history = env.get_history()  # List[StateTransition]
first_transition = history[0]
print(first_transition.action)     # 型安全なアクセス
print(first_transition.reward)     # floatであることが保証

履歴データへのアクセスが型安全になり、ランタイムエラーを減らせます。

グリッドワールドで遊んでみる

実装したグリッドワールド環境を使って、(0,0)から(2,2)のゴールまでstepで移動してみましょう：

def play_gridworld_game():
    """グリッドワールドでゴールを目指すゲーム"""
    env = GridWorldEnvironment(size=3, stochastic=False)
    
    # ゲーム開始
    observation = env.reset(start_position=(0, 0))
    print(f"ゲーム開始！ 位置: {observation}")
    print(f"ゴール: {env.goal}")
    print("-" * 30)
    
    total_reward = 0
    step_count = 0
    
    # 最適経路: 右→右→下→下
    actions = ["right", "right", "down", "down"]
    
    for action in actions:
        step_count += 1
        observation, reward, done, info = env.step(action)
        total_reward += reward
        
        print(f"ステップ {step_count}: {action}")
        print(f"  位置: {observation}")
        print(f"  報酬: {reward}")
        print(f"  累積報酬: {total_reward}")
        
        if done:
            print(f"🎉 ゴール到達！ 総ステップ数: {step_count}")
            break
        print()
    
    print(f"\n最終結果:")
    print(f"  総報酬: {total_reward}")
    print(f"  移動コスト: {step_count - 1} × {env.move_cost} = {(step_count - 1) * env.move_cost}")
    print(f"  ゴール報酬: {env.goal_reward}")
    
    # 履歴の確認
    history = env.get_history()
    print(f"\nエピソード履歴:")
    for i, transition in enumerate(history):
        print(f"  {i+1}. {transition.previous_state} --{transition.action}--> {transition.next_state} (報酬: {transition.reward})")

# 実行例
play_gridworld_game()

実行結果:

ゲーム開始！ 位置: (0, 0)
ゴール: (2, 2)
------------------------------
ステップ 1: right
  位置: (0, 1)
  報酬: -0.1
  累積報酬: -0.1

ステップ 2: right
  位置: (0, 2)
  報酬: -0.1
  累積報酬: -0.2

ステップ 3: down
  位置: (1, 2)
  報酬: -0.1
  累積報酬: -0.3

ステップ 4: down
  位置: (2, 2)
  報酬: 1.0
  累積報酬: 0.7
🎉 ゴール到達！ 総ステップ数: 4

最終結果:
  総報酬: 0.7
  移動コスト: 3 × -0.1 = -0.3
  ゴール報酬: 1.0

エピソード履歴:
  1. (0, 0) --right--> (0, 1) (報酬: -0.1)
  2. (0, 1) --right--> (0, 2) (報酬: -0.1)
  3. (0, 2) --down--> (1, 2) (報酬: -0.1)
  4. (1, 2) --down--> (2, 2) (報酬: 1.0)

この例では、4ステップでゴールに到達し、移動コスト（-0.3）を差し引いても正の総報酬（+0.7）を得られました。Pydanticによる型安全な履歴管理により、各ステップの詳細な記録を簡単に確認できます。

コードの入手と実行

この記事で紹介したコードは、以下のGitHubリポジトリで公開されています：

🔗 rl-src: 強化学習MDPライブラリ

リポジトリには以下が含まれています：

本記事で解説した全てのコード
20個のテストケースで検証済みの実装
MDPの性質を実証するサンプルプログラム
詳細なドキュメントとAPIリファレンス

クイックスタート

# リポジトリのクローン
git clone https://github.com/takuyakubo/rl-src.git
cd rl-src

# 依存関係のインストール  
uv install

# テストの実行（全20テストが通ることを確認）
uv run pytest

# MDPデモンストレーションの実行
uv run python examples/mdp_demonstration.py

次の記事では、この環境を使って実際の強化学習アルゴリズムを実装していきます。

まとめ

マルコフ決定過程は、内部状態が完全に観測可能という仮定の下で、強化学習問題を数学的に厳密かつ扱いやすい形で定式化する枠組みです。重要なポイントを振り返ってみましょう：

MDPの核心的な性質:

マルコフ性: 現在の状態が将来を予測するのに十分な情報を含む
時不変性: 環境の規則が時間によって変化しない
環境の記述: MDPは環境側の仕様を定義する

実装を通じた理解: 型安全で拡張可能なPython実装により、MDPの抽象的な概念が具体的にどう動作するかを体験できました。Generic型やPydanticモデルを活用した設計で、マルコフ性と時不変性を保ちながらコードの可読性と保守性を向上させることができました。

この枠組みは、多くの強化学習アルゴリズムの理論的基盤となっており、価値反復法、方策反復法、Q学習などの代表的な手法は全てMDPの枠組みで設計されています。次の記事ではAgent側の振る舞いについてみていきます。