Zenn
株式会社COMPASS
🔎

LLMを活用して問題間の類似度を推定した話

中本さや香
2024/05/02に公開
自然言語処理
GPT-4
OpenAI
LLM
類似度検索
tech

こんにちは！株式会社COMPASSのデータ・AIユニットのR&D部でAIエンジニアをしている中本です！現在は主に生成系AIを用いた技術検証や、実際の開発現場での活用を目指した研究開発を行っています。日々試行錯誤を続ける業務で、頭を悩ませることも多いですが、そんな時は大好きな日本茶を飲んで頭をリフレッシュさせています！

今回はLLMを活用して、キュビナに搭載されている問題同士の類似度を推定する取り組みについて、どのような過程でどのように精度を高めていったかというところについてご紹介したいと思っています。

この記事はこんな方におすすめ

  • 株式会社COMPASSの技術的な取り組みについて知りたい方
  • LLMを用いたテキストのベクトル化、コサイン類似度の推定について知りたい方
  • テキストデータの類似度判定の精度向上手法について知りたい方

背景

COMPASSでは、AIが子どもたち一人ひとりに合った問題を出題する公教育向けのデジタル教材「キュビナ」を開発、提供しています。キュビナは小学校、中学校向けの国語、算数・数学、理科、社会、英語の5教科の問題を搭載しており、その数は8万問以上となっています。そしてその問題について、活用状況を分析した上で必要な問題の追加、改善が必要な問題のアップデートを日々行っています。

キュビナを構成する問題を作っていく上で重要な考え方の一つに「ナノステップ」というものがあります。これは学習を進める上で、出題する問題の難易度の階段をできる限り細かくすることで、つまずくことなく学習を進められるというものです。ナノステップを実現するためには、キュビナにどのような問題が搭載されているか、搭載されている問題同士の関係性がどのようになっているかを分析しながら、必要な問題の追加や修正を行う必要があります。今まではコンテンツ企画開発部という問題作成に特化したチームがしっかりと時間をかけそういった分析を行っていました。しかし膨大な量の問題に対してそれを人力で行い続けるのはコストがかかります。そこで、問題の関係性がどのようになっているか、具体的には問題の類似度の推定をLLMを活用することでより効率的に行えないかと考えました。

そういった分析を行うために、以前「数式やイラストを含む画像をOCRやLLMを使ってテキスト化した話」でご紹介したように、問題をテキストで表現するという取り組みを行ってきました。
以前の記事はこちら。

類似度推定を行おうとした際に、アプローチは複数考えられますが、今回は下記のステップで検証を行い、最終的に一定の精度で類似度推定を行うことができるようになりました。

  1. 問題テキストそのものを用いた類似度推定
  2. 問題を要約したテキストデータを用いた類似度推定
  3. 問題テキスト、要約したテキストデータをハイブリッドに用いた類似度推定

それでは、各ステップで行った検証プロセスと結果についてご紹介したいと思いますが、まずは問題の類似度推定について、そもそもどういうことがやりたかったかを具体的にご説明したいと思います。

問題の類似度推定について

類似度といっても、何を基準として類似している、類似していないを判断するかによって期待する結果が異なります。今回は問題の類似度について下記のような基準で推定を行うこととしました。

  • 類似度が高い
    • 問題を出す意図、学習到達目標が近い
  • 類似度が低い
    • 問題を出す意図、学習到達目標が異なる
    • 単元が異なる

具体的な例で見ていきましょう。ここでは数学の問題の例を4つほど用意しました。

A B
C D

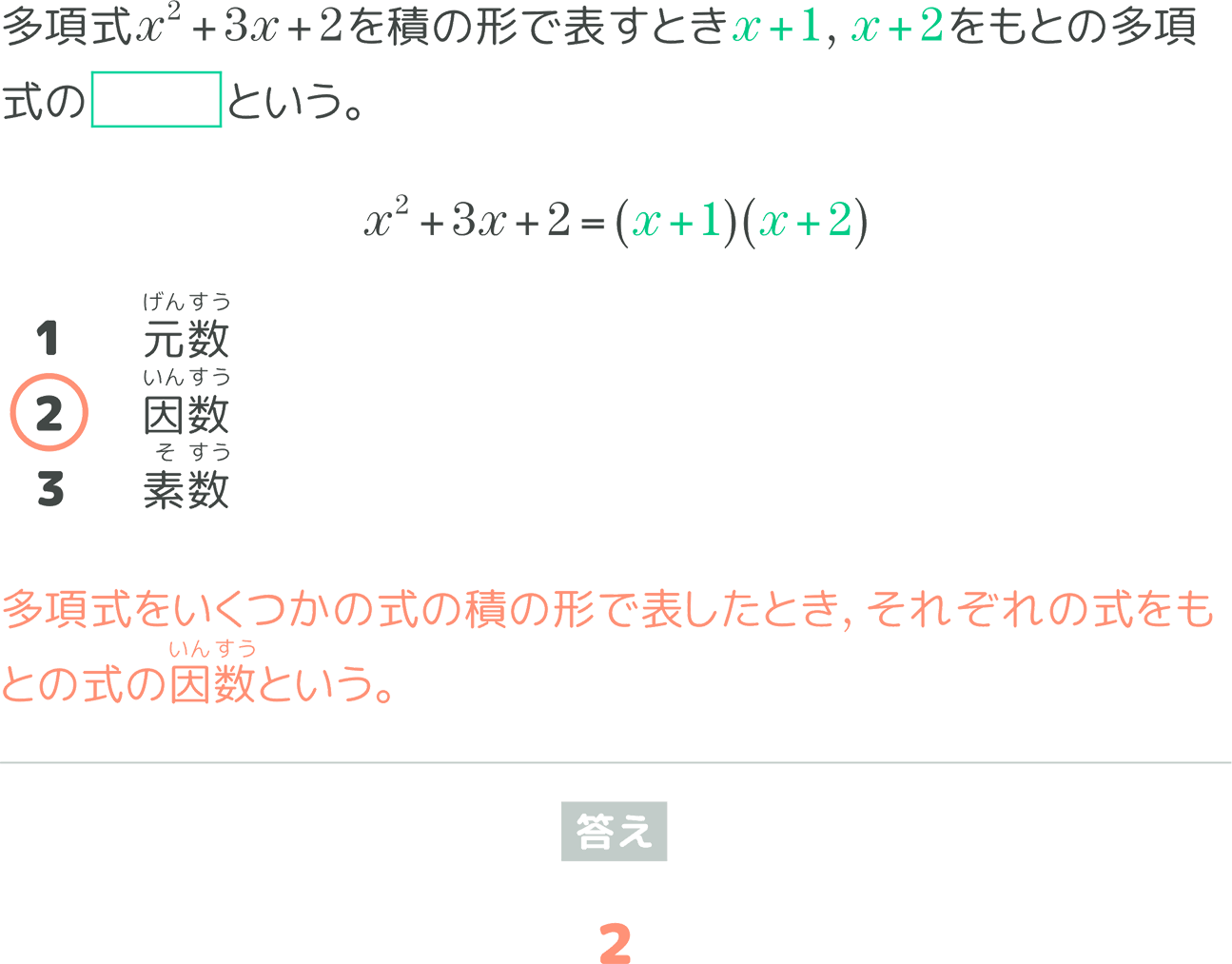
キュビナに搭載されている数学の問題例

それぞれA、Bの問題は正負の数を使った加法ができるかを問う問題、Cの問題は因数分解の基礎知識を問う問題、Dの問題は正負の数を使った減法ができるかを問う問題となっています。そこで、Aから見た時に、B、C、Dとの類似度はどうなっているか？について上記の基準に則って考えていきます。

この時、AとBの問題は問題を出す意図、学習到達目標が同じということで、問題文で使われている数字の差異はありますが、類似度が高いと考えられます。次にAとCの問題はそもそも単元が違うということで類似度が低いと考えられます。最後にAとDは見た目は近い問題になりますがAは加法ができるかを問う問題であるのに対してDは減法ができるかを問う問題となっているので、問題を出す意図という点についてAとBの類似度に対しては類似度が低いと考えられます。

このように、一見すると似ているように見える問題でも出題意図が異なっているものや、単元が違うなど学習到達目標が違うものについてはしっかりと類似度が低いものとして取り扱えるようにしたいというのが期待する結果となります。それではこの基準に則って類似度が推定できるか、試していきましょう。

問題テキストを用いた類似度推定

まずはシンプルにテキスト化されたキュビナの問題データを用いて類似度推定を行いました。手法としては下記のように行いました。

  1. 問題テキストのベクトル化
  2. コサイン類似度を用いた類似度推定

まずは問題テキストをベクトル化していきます。テキストのベクトル化はテキスト表現を複数次元の数値データに変換する手法で、自然言語処理の世界では一般的に用いられています。今まで様々な手法が用いられてきましたが、今回はOpen AIのEmbeddingsのAPIを使ってベクトル化を行いました。OpenAIのEmbeddingsのAPIを用いた手法は非常に簡単で、このように少ないコード量でベクトル化を行うことができます。下記はGoogle Apps Scriptを用いたコード例となります。

const OPENAI_API_KEY = PropertiesService.getScriptProperties().getProperty('OPENAI_KEY'); /* OpenAI API Keyをスクリプトプロパティに登録しておくこと。 */
const EMBEDDINGS_MODEL = "text-embedding-3-large"; /* 任意のモデル名 */
const OPENAI_EMBEDDINGS_URL = "https://api.openai.com/v1/embeddings";
/* OpenAI Reference : https://platform.openai.com/docs/api-reference/embeddings */


function callOpenAIEmbeddingsAPI(target_text) {
    const payload = {
        model: EMBEDDINGS_MODEL,
		input: target_text,
    /* 他に設定可能なパラメータは、OpenAIのreferenceを参照してください */
	};
	const options = {
		method: "post",
		contentType: "application/json",
		headers: {
			Authorization: "Bearer " + OPENAI_API_KEY,
		},
		payload: JSON.stringify(payload),
	};
	try{
		const response = UrlFetchApp.fetch(
            OPENAI_EMBEDDINGS_URL,
            options,
        );
        const json_response = JSON.parse(response.getContentText());
        /* json_responseの中身 */
        /*{
            "object": string,
            "data": [
                {
                    "object": string,
                    "embedding": list(出力結果),
                    "index": int
                }
            ],
            "model": "text-embedding-ada-002",
            "usage": {
                "prompt_tokens": int,
                "total_tokens": int
            }
        }*/
        return json_response.data[0].embedding;
	}catch (e){
		throw (e)
    };
}

Open AIのEmbeddingsのAPIを用いたベクトル化のコード例(Google Apps Script)

ベクトル化された情報をもとに類似度を推定していくので、数学に搭載されている問題テキストをあらかじめ上記手法を用いて全てベクトル化しました。これで類似度を推定したい問題のベクトル表現と、搭載されている問題の類似度を推定していく準備ができました。

次に、ベクトル化したテキスト同士の類似度を判定するためにコサイン類似度を用いた推定を行っていきます。コサイン類似度は二つのベクトル間の角度に基づいて、それらの類似性を測定する手法で、こちらもテキストデータの比較において一般的に用いられている手法となっています。実際にコサイン類似度を算出する数式はこちらになります。分母は各ベクトルのノルム（ベクトルの大きさ）の和、分子はベクトルの内積になっています。

cosineSimilarity(x,y) = \frac{\sum_{k=1}^n (x_k y_k)}{\sqrt{\sum_{k=1}^n x_k^2}+\sqrt{\sum_{k=1}^n y_k^2}}

ここで、nは2つのベクトルx、yの次元数

数学が苦手な人が見たらびっくりするような数式ではありますが、実際の計算自体はコードに直すと非常に簡単に実現できます。ここではコサイン類似度を計算する関数を用意してみました。

function cosineSimilarity(vec2, vec2){
let dotProduct = 0; /* ベクトルの内積 */
    	let normVec1 = 0; /* vec1のノルム */
    	let normVec2 = 0; /* vec2のノルム */
    	for (let i = 0; i < vec1.length; i++) {
      		dotProduct += vec1[i] * vec2[i];
           	normVec1 += vec1[i] * vec1[i];
           	normVec2 += vec2[i] * vec2[i];
    	}
    	normVec1 = Math.sqrt(normVec1);
    	normVec2 = Math.sqrt(normVec2);
    	if (normVec1 === 0 || normVec2 === 0) {
           	return 0;
    	}
    	const similarity = dotProduct / (normVec1 * normVec2);
    	return similarity;
}

コサイン類似度を計算する関数

各問題のベクトル化されたデータと、それらを比較する関数ができたので、いよいよ類似度推定を行う準備が整いました。ということで、実際の問題で試してみましょう！

推定は下記のような流れで行います。

  1. 類似度を推定したい問題を用意
  2. 用意された問題のベクトルデータと、搭載されている問題のベクトルデータとのコサイン類似度を算出
  3. 算出されたコサイン類似度が最も高かった問題を確認

まず1問目はこちら。

以下の問題を解きなさい。ある長方形のマス目の図があります。縦が6マス、横が8マスで構成されています。1マスの一辺の長さが1cmです。この長方形の面積を求めなさい。
48cm²

この問題に対して最も類似度が高いと推定された問題がこちらです。

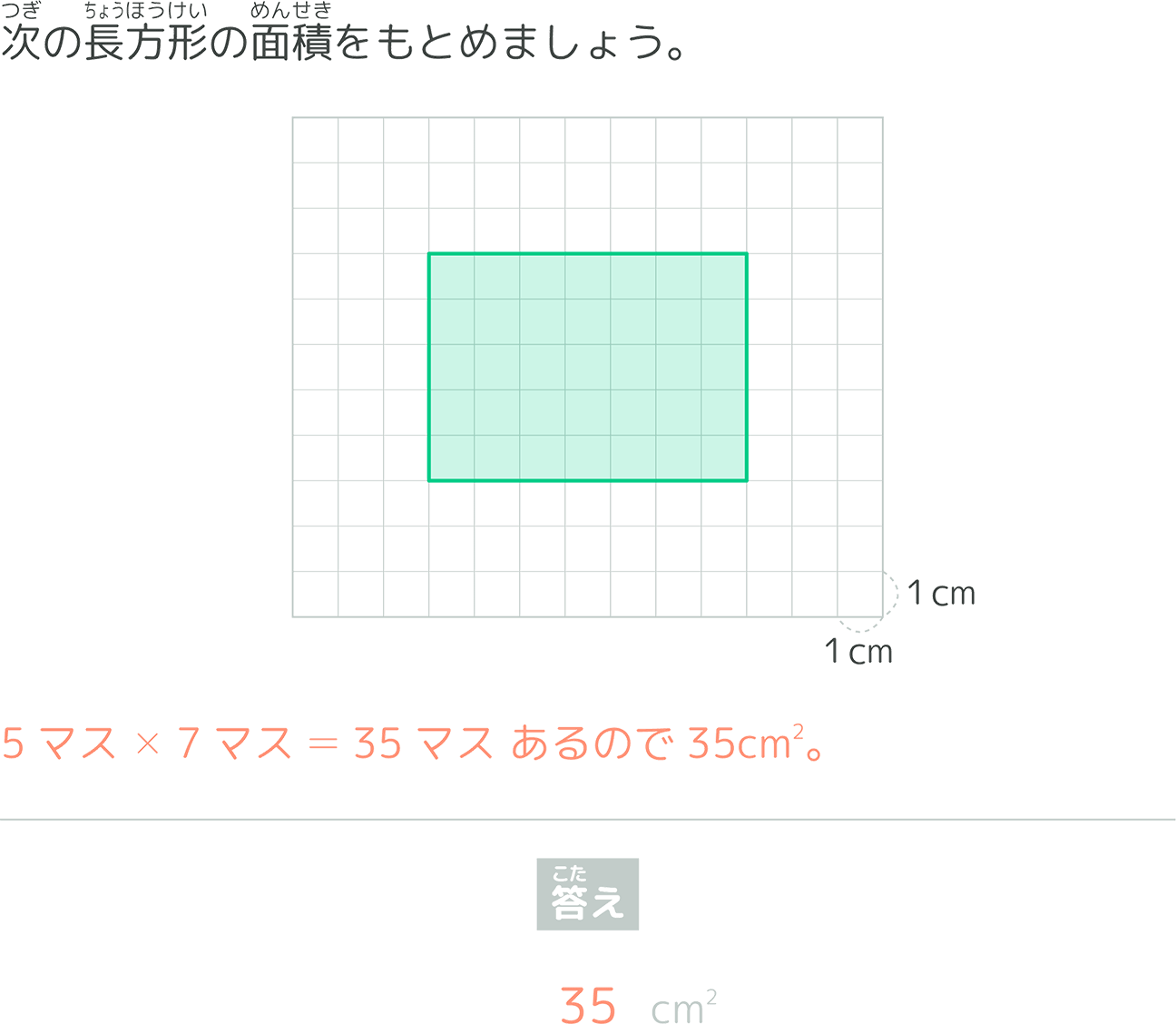
マス目を使った面積を求める問題が類似度の高い問題として出てきました！これはかなり精度高く出てきている気がします！他の問題でも試してみましょう。

以下の計算をしなさい。7×8
56

こちらの問題に対して最も類似度が高いと推定された問題がこちらです。

こちらに関しては一桁の数の掛け算ができるかどうかを問う問題を期待していたところなのですが、そもそも単元から異なる問題が類似度が高い問題として推定されました。

今回の結果について、問題テキストに一定の分量があり、内容にわかりやすい特徴が含まれる場合には比較的高い精度で類似度の推定ができるのではないかと考えています。一方で、問題テキスト自体が短かったり、内容に特徴がない場合には精度面で期待には届かないと考察しました。

問題を要約したテキストデータを用いた類似度推定

問題テキストだけでは精度が出なかったので、今度は問題を要約したテキストを用いた類似度推定を行ってみることにしました。手順としては問題テキストを用いた類似度推定とほとんど同じにはなりますが下記のように行いました。

  1. 問題文から問題を要約したテキストを作成
  2. 要約したテキストのベクトル化
  3. コサイン類似度を用いた類似度判定

まずは問題文を要約したテキストを作成していきます。要約を作る上では、事前に要約フォーマットとパラメーター（この問題のゴール、問題の難易度、など）を定義して、それに則った形で出力するようなプロンプトを組み、LLMに機械的に要約を作成させました。先ほどの問題に対して要約を作成するとこのようになります。

1問目の問題本文

以下の問題を解きなさい。ある長方形のマス目の図があります。縦が6マス、横が8マスで構成されています。1マスの一辺の長さが1cmです。この長方形の面積を求めなさい。
48cm²

1問目の要約

{
"learning_unit": "面積の求め方",
"intent": "長方形の面積を求める公式を理解し、実際に適用する",
"goal":[
"長方形の面積を求める公式を使って計算すること"
],
"prerequisites": [
"掛け算の計算",
"長方形の面積の公式（縦×横）",
"単位の理解（平方センチメートル）"
],
"analysis_process":"問題文から、長方形の縦と横のマス目の数が与えられており、1マスの一辺の長さが1cmであることが分かります。これをもとに面積を求めるためには、長方形の面積を求める公式（縦×横）を知っている必要があります。また、掛け算ができること、面積の単位が平方センチメートルであることの理解も必要です。これらの知識を用いて、6マス×8マス=48マスと計算し、1マスが1cm²であることから、48cm²と面積を求めることができます。",
"level":"知識を使用する基本問題"
}

ここから先の手順は問題テキストを用いた類似度推定と同じで、要約したテキストをベクトル化した上でコサイン類似度を推定するという流れになります。ということで実際に問題テキストで類似度を推定した問題と同じもので試してみましょう！

まずは上記の1問目に対して最も類似度が高いと算出された問題がこちらです。

うーん、惜しい！長方形の面積を求める問題という点では、そこまでかけ離れてはいないのですが、実際にマス目を使って面積を計算する問題がキュビナに搭載されているという点も踏まえると、こちらの問題に対しては問題テキストのみを使った類似度推定の方が期待する結果に近かったと思います。（とはいえ全く外れてるわけではない）

それでは次にもう一つの問題も試してみましょう。
2問目本文

以下の計算をしなさい。7×8
56

2問目の要約

{
"learning_unit": "掛け算の計算",
"intent": "基本的な掛け算の計算能力を確認する",
"goal":[
"掛け算の計算スキルの習得"
],
"prerequisites": [
"数の概念の理解",
"足し算の基本的なスキル",
"掛け算の表や暗記を通じた基本的な掛け算の理解"
],
"analysis_process":"この問題は単純な一桁の数同士の掛け算であり、小学校低学年の算数の授業で扱われる基本的な内容です。問題の意図は、学生が掛け算の基本を理解し、正確に計算できるかを確認することにあります。掛け算の基本的なスキルが必要であり、これには数の概念の理解と足し算のスキルが前提となります。",
"level":"知識定着のための問題"
}

そして、この問題について最も類似度が高いと推定された問題がこちらです。

すごい、今度はしっかり掛け算の基本的なスキルを問う問題が類似度の高い問題として推定されています！

このように、問題を要約したテキストを用いた手法では、問題テキストそのものに特徴があるような問題に対しては問題テキストを使った手法と比較して精度が落ちるようです。一方で問題テキストが短かったり、表現力が乏しい際には、要約したテキストを用いることで、今回の類似度の基準である「問題を出す意図、学習到達目標の近さ」を適切に表現でき、類似度推定の精度が高くなったのではないかと考えています。

問題テキスト、要約したテキストをハイブリッドに用いた類似度推定

今までの検証で、問題テキスト、要約したテキストを用いた手法はそれぞれ得意不得意があることがわかりました。そこで、それぞれのいいとこ取りをしてみようということで、両方の手法をハイブリッドに用いた類似度推定手法を検討しました。本手法では次のような手順で類似度推定を行いました。

  1. 問題テキストを用いた手法での類似度ランクを出す
  2. 要約したテキストを用いた手法での類似度ランクを出す
  3. それぞれの類似度ランクに重み付けを行い、再ランキングを行う

ポイントとしては手順3で、類似度ランクに重みづけを行うことでより細かい出力結果を調整しています。具体的な数式としては下記となります。

HybridScore = \frac{w_{plain}}{r_{plain}} + \frac{w_{summary}}{r_{summary}}

ここで、r_{plain}、r_{summary}はそれぞれ、本文ランキング内での順位と要約ランキング内での順位になっています。また、w_{plain}、w_{summary}は重みパラメータです。

w_{plain}（問題テキストを用いた手法の重み）、w_{summary}（要約したテキストを用いた手法の重み）で表された重みの合計値が1となるように、w_{plain}、w_{summary}をそれぞれ0より大きく、1未満となる値で設定することで、どちらの手法での出力により信頼を置くかを決めることができます。そしてここで重要になってくるのは各手法に対する適切な重みの値設定です。そこで、このユースケースにおいて最適な重みの値を探るために実験を行いました。実験の内容としては、類似度を推定したい問題群に対して、上記数式を用いて複数の重み付けのパターンによって推定されたランキングと、人間が最も類似していると考える問題を比較するというものです。具体的には100問弱の問題に対して、各重み付けのパターンにおける類似度ランクを出し、その10位以内に人間が最も類似すると考えて選んだ問題が含まれる割合を検証しました。その検証結果が下記の表になります。

w_{plain} w_{summary} 10位以内に現れた割合
1.0 0.0 0.368
0.6 0.4 0.471
0.5 0.5 0.483
0.4 0.6 0.494
0.3 0.7 0.483
0.0 1.0 0.540

結果としては、要約テキストのみを用いた手法が、最も人間が選んだ問題を含む割合が高いということがわかりました。また、ハイブリッドな手法を用いた場合、重み付けの値としてはw_{plain}を0.4、w_{summary}を0.6とした場合に最も結果が良くなることが分かりました。一見要約の方が良い結果を出しているように見えますが、上記はあくまで割合の話で、中身を覗いてみるとハイブリッドな手法のランクの中にしか出現しない問題もありました。

そこで、実際の問題を用いて結果を比較してみましょう。今回類似度を推定する問題としては下記の問題を利用します。

問題

サイコロを2つ振る時に、両方とも同じ目が出る確率を求めなさい

要約

{
"learning_unit": "確率の計算",
"intent": "同様に確からしい場合の確率の計算方法を理解させる",
"goal":[
"基本的な確率の計算方法を学ぶ",
"具体的な事象に対して確率を適用する方法を理解する"
],
"prerequisites": [
"全事象の数の計算方法",
"有利な事象の数の計算方法",
"分数の計算"
],
"analysis_process":"この問題は、サイコロを2つ振った時に両方とも同じ目が出る確率を求める問題です。この問題から、生徒は全事象と有利な事象を理解し、それらを用いて確率を計算する方法を学ぶことができます。サイコロが2つあるため、全事象は6×6=36通りとなります。有利な事象（両方とも同じ目）は、(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)の6通りです。したがって、確率は6/36 = 1/6となります。この計算過程を通じて、生徒は確率の基本的な計算方法を学ぶことが目的です。",
"level":"知識を使用する基本問題"
}

それでは、問題テキストのみを用いた手法、要約したテキストのみを用いた手法、ハイブリッドな手法それぞれで推定された類似度ランクを見てみましょう。

順位 本文ランキング 要約ランキング ハイブリッドランキング
1 ⭕️サイコロ2つの問題 🔺サイコロ1つの問題 ⭕️サイコロ2つの問題
2 ⭕️サイコロ2つの問題 ⭕️サイコロ2つの問題 🔺サイコロ2つの問題だが場合の数の問題
3 ⭕️サイコロ2つの問題 ⭕️サイコロ2つの問題 ⭕️サイコロ2つの問題
4 ⭕️サイコロ2つの問題 🔺サイコロ1つの問題 ⭕️サイコロ2つの問題
5 ❌サイコロの問題じゃない 🔺サイコロ1つの問題 ⭕️サイコロ2つの問題

まずは問題テキストのみを用いた類似度ランクについてです。確率の問題を拾ってきてはいるものの、5位の問題はサイコロではなくコインを投げる問題になっています。元々問題テキストのみを用いた類似度ランクは実験においても期待する結果が出せなかったこともあり、この結果は頷けるかなと思います。次に要約したテキストとハイブリッドでの類似度ランクについてです。こちらは両方ともサイコロを用いた確率の問題を拾ってきています。しかしながら、要約したテキストを用いた手法ではサイコロを2つ用いた問題が2問しか含まれていないのに対して、ハイブリッドな手法では全てサイコロを2つ用いた問題となっています。このように、実験では要約したテキストのみを使った手法が最も良い結果を残しましたが、問題の種類や利用シーンによってはハイブリッドな手法を用いた結果の方が納得感が高い可能性があるという結果となりました。

まとめ

今回はLLMを活用して問題間の類似度を、問題のテキストを用いた手法、問題を要約したテキストを用いた手法、それらをハイブリッドに用いた手法にて推定しました。

結果として、どのシチュエーションでも精度が高いと言える手法を見出すことはできませんでしたが、各手法で比較的納得感の高い類似度推定ができたと考えています。また、今回は類似度が適切に推定できることがゴールであって、そのための手法を絞ることがゴールではないので、複数の手法の出力を見比べながら効率的に適切な情報を選べるようになったというだけでも非常に大きな意義があると考えています。今後もCOMPASSではこのようにLLMのような新しい技術を使った課題解決を行っていきたいと考えています。

最後に、ここまでお読みいただいてありがとうございました。本記事が皆様の課題解決の一助になれば幸いです。

株式会社COMPASS
株式会社COMPASS

学習eポータル＋AI型教材「Qubena（キュビナ）」を開発している株式会社COMPASSのテックブログです！

Discussion