Pinocchioの原理

はじめに

前提知識

• 群、体に関する初歩的な知識(準同型、単射全射、巡回群、生成元など)

扱う内容

• zk-SNARKsとは？
• Pinocchio(最も基本的なzk-SNARKs)の解説

zk-SNARKsとは

zk-SNARKはZero Knowledge Succinct Non-interactive Argument of Knowledgeの省略形です。それぞれの単語を日本語訳しますと

Zero Knowledge:ゼロ知識の
Succinct: 簡潔な
Non-interactive: 非対話の
Argument of Knowledge: 知識の根拠^[1]

という意味になります。zk-SNARKの具体的なプロトコルは複数知られているので、それらを総称してzk-SNARKsと呼びます。

次の図はzk-SNARKの一例を表しています。

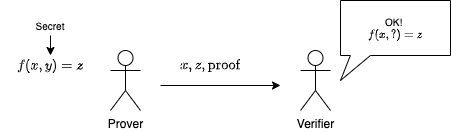zk-SNARKの概要

Proverは、ある関数$f$に対して、$f(x, y) = z$が成り立つ$x, y, z$を知っているとします。目的は、Verifierに、$y$を秘密にしたまま$f(x, y) = z$が成り立つことを納得してもらうことです。Prover、Verifierは事前に$f$がどのような関数であるか共有しているとします。

Proverは$f(x, y) = z$が成り立っていることの「証明」proofを作成します。proofには$y$に関する情報は含まれていません。Verifierはproofを用いて検証を行い、ステートメント「$x, z$に対して$y$が存在し$f(x, y) = z$が成り立つ」を受理するか拒否するかを決定します。

驚くべきことに、proofのサイズは、$f(x, y)$の計算量と無関係、あるいは対数程度に小さくできます。一般的なzk-SNARKプロトコルでは、Verifierの検証時間はproofのサイズと同程度なので、Verifierは$f(x, y)$を直接計算するよりも遥かに効率的に$f(x, y) = z$を検証することができます^[2]。

この例をzk-SNARKの定義に対応させると

Zero Knowledge(ゼロ知識の):Verifierに与える$y$の知識はゼロ
Succinct(簡潔な): proofのサイズは$f(x, y)$の計算量に対して非常に小さい(対数程度に小さい、または一定サイズ)
Non-interactive(非対話の): ProverからVerifierへの一回きりの通信のみ行う
Argument of Knowledge(知識の根拠): $f(x, y) = z$が成り立つ$y$を知っていることの根拠(証明)

となります。Proverはどのような証明をどうやって作るか、Verifierは証明をどう検証するか、というところがzk-SNARKプロトコルの肝であり、これまでに様々なzk-SNARKプロトコルが提案されてきました。

Pinocchioとは

Pinocchioとは、2013年にBryan Parno, Jon Howell, Craig Gentry, Mariana Raykovaの4人が"Pinocchio: Nearly Practical Verifiable Computation"という論文で発表したzk-SNARKプロトコルです。

原論文
https://eprint.iacr.org/2013/279

zk-SNARKsの中ではかなりシンプルで基本的なプロトコルです。

状況設定

前のセクションでは、公開引数$x$と秘密引数$y$を持つ関数$f(x, y)$を扱いましたが、ここでは関数$y = F(u)$を扱います。ただし$u$は$n$個の変数の組$u:=(u_1, u_2, \ldots, u_n)$で、$y$は$n'$個の変数の組$y:=(y_1, y_2, \ldots, y_{n'})$とします。最初に$u$が公開引数の場合を論じ、次に$u$の一部を秘匿化する(ゼロ知識化する)方法について述べます。

プロトコルの流れ

Pinocchioでは信頼できる第三者による事前のセットアップ(トラステッドセットアップ)が必要です。信頼できる第三者は証明の作成に使う評価鍵(Evaluation Key)EKと、検証に使う検証鍵(Verification Key)VKを生成して公開します。ProverはEKを用いて証明$\pi$を作成し$u, y$とともにVerifierに送ります。VerifierはVKと$u,y, \pi$を用いて証明を検証します。

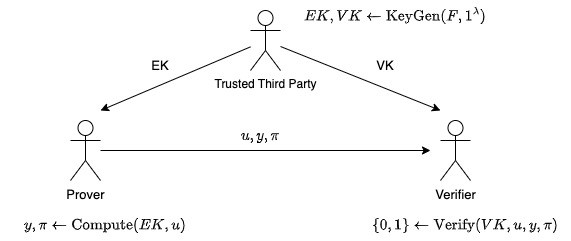トラステッドセットアップが必要なzk-SNARK

図中の$\lambda$はセキュリティの程度を表す整数で、大きくすれば証明が偽造しにくくなる一方で、$EK,VK$のサイズは大きくなります。

Proverは$y=F(u)$というステートメントを多項式の割り算の問題へ変換し、それを元に証明$\pi$を作成します。証明$\pi$は群の元の組であり、Verifierはペアリングを用いて$y=F(u)$を検証します。

多項式へのエンコード(QAP)

Pinocchioでは$F$を算術回路で表し、それを多項式の割り算の問題へ変換します。算術回路がエンコードされた多項式をQAP(Quadratic Arithmetic Program)と言います。この節では、どのように$F$をQAPに変換するかを解説します。

$y_1 = (u_1 + u_2)u_3u_4$という関数を考えてみましょう。これは下図のような算術回路で表すことができます。

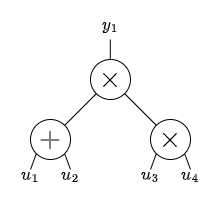
例えば$u_1=2,u_2=1,u_3=2,u_4=3$を代入すると下図のようになります。

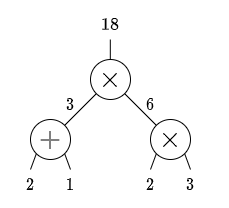
$u_1=c_1, u_2=c_2,u_3=c_3,u_4=c_4$のとき、新たにワイヤに割り当てられる数値を$d$,$e$,$f$とすると(図)、

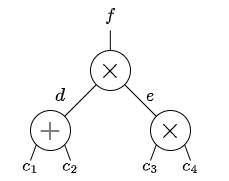
それぞれのゲートにおいて次のような制約が課せられます。

$$\begin{align*} c_1 + c_2 = d\\ c_3 \times c_4 = e\\ d\times e = f \end{align*}$$

ただし、制約はなるべく少ないほうが良いので、足し算のゲートに関しては制約を課さずに、その次の掛け算のゲートにおいて制約を課すことにします。

$$\begin{align*} c_3 \times c_4 = e\\ (c_1+c_2)\times e = f \end{align*}$$

すなわち、$c_1 + c_2 = d$というような足し算ゲートの制約に関しては、その値を入力として利用する掛け算ゲートの制約に代入することで制約の数を減らすということです。結局、制約は掛け算ゲートにおいてのみ発生し、またそのゲート出力として新たにワイヤの値が割り当てられることになります。新たに割り当てられるワイヤの値$e,f$を$c_5, c_6$と書き直すことにします。また、$c_5$, $c_6$が割り当てられる掛け算ゲートをそれぞれゲート5, ゲート6と呼ぶことにします。すると制約は次のように書けます。

$$\begin{align*} c_3 \times c_4 = c_5\qquad(gate5)\\ (c_1+c_2)\times c_5 = c_6\qquad(gate6) \end{align*}$$

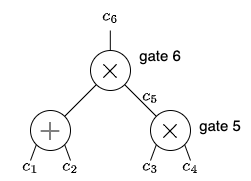
これらの制約を体$\mathbb{F}_p$上の多項式$v_k(x)$, $w_k(x)$, $y_k(x)$ ($k=1,2,3,4,5,6$)を使って表します。$\mathbb{F}_p$から適当に2点$r_5, r_6$を選んでおきます。$r_5$がゲート5、$r_6$がゲート6における多項式の評価点となります（後で意味を解説します）。

ゲートの制約の式は$(c_iの和)\times(c_iの和)=c_j$の形になることに注意してください。ゲートの制約の式の左辺について、$\times$に対して左の項を「左項」、右の項を「右項」と呼ぶことにします。例えばゲート5の制約$c_3\times c_4 = c_5$において、「左項」は$c_3$、「右項」は$c_4$になります。

$v_k(x)$は「左項」に、$w_k(x)$は「右項」に、$y_k(x)$は右辺に$c_k$が含まれるかどうかを表す多項式です。

ゲート5の制約において、もし「左項」に$c_k$が含まれていれば$v_k(r_5)=1$、含まれていなければ$v_k(r_5)=0$、ゲート6の制約において、もし「左項」に$c_k$が含まれていれば$v_k(r_6)=1$、含まれていなければ$v_k(r_6)=0$となるように$v_k(x)$を構成します。$w_k(x)$は「右項」に対して、$y_k(x)$は右辺に対して同様に構成します(表)。

$v_k(x)$, $w_k(x)$, $y_k(x)$の構成(Parno et al. 2013からの引用)

例えば$v_1(x)$は次のように構成できます。ゲート5の制約は$c_3\times c_4 = c_5$で、「左項」は$c_3$であり、$c_1$は含まれません。従って$v_1(r_5) = 0$です。ゲート6の制約は$(c_1 + c_2)\times c_5 = c_6$で、「左項」は$c_1+c_2$であり、$c_1$が含まれます。従って$v_1(r_6) = 1$です。もし仮に$r_5=1$, $r_6=2$を選ぶなら、$v_1(x) = x-1$と表すことができます。

このように多項式$v_k(x)$, $w_k(x)$, $y_k(x)$を構成すると、制約の式は

$$\left( \sum_{k=1}^{6} c_k v_k(x) \right)\left( \sum_{k=1}^{6} c_k w_k(x) \right) = \sum_{k=1}^{6} c_k y_k(x) \quad \text{where } x=r_5, r_6$$

とまとめることができます。

右辺を左辺に移項し、$p(x)$と置いてみます。

$$\begin{align*} p(x):= \left( \sum_{k=1}^{6} c_k v_k(x) \right)\left( \sum_{k=1}^{6} c_k w_k(x) \right) - \sum_{k=1}^{6} c_k y_k(x) \end{align*}$$

$p(x)$は$x=r_5, r_6$を根に持つので、$t(x):=(x-r_5)(x - r_6)$で割り切ることができます。逆に$p(x)$が$t(x)$で割り切るならば、$p(x)$は$x=r_5, r_6$を根に持ち、掛け算ゲートの正しい制約式が得られるので$\{c_k\}$が正しく割り当てられていることがわかります。

以上により、「$\{c_k\}$は回路の正しい値の割り当てか」という問題を、「$p(x)$が$t(x)$で割り切れるか」という問題に変換することができました。

今回は、定数入力を含まない回路を取り上げましたが、一般的には回路には$c_k$だけでなく定数が入力されることもあります。その場合、定数を表す多項式$v_0(x)$, $w_0(x)$, $y_0(x)$を加える必要があります。例えばゲート6の制約が$(c_3 + 2)\times c_5 = c_6$ならば、$v_0(r_6)=2$となるように$v_0(x)$を構成します。

以上をまとめると、次のようになります。

定理
関数$F$と評価点の集合$\mathcal{M}$、それに対応する$\{v_k(x)\}_{k=0,\ldots,m}$, $\{w_k(x)\}_{k=0,\ldots,m}$, $\{y_k(x)\}_{k=0,\ldots,m}$が与えられているとき、$c_1,\ldots, c_{m}\in \mathbb{F}_p$が関数$F$に対応する算術回路の正しい値の割り当てであることは、$t(x) := \prod_{r_g \in \mathcal{M}} (x -r_g)$が

$$\begin{align} p(x):= \left( v_0(x) + \sum_{k=1}^{m} c_k v_k(x) \right)\left( w_0(x) +\sum_{k=1}^{m} c_k w_k(x) \right) -y_0(x) - \sum_{k=1}^{m} c_k y_k(x) \end{align}$$

を割り切ることの必要十分条件。ただし$N:=n+n'$は入力/出力変数の合計数で、$c_{1}, \ldots, c_{N}$は$F$の入出力に対応するワイヤに割り当てられる値であり、$c_{N+1}, \ldots, c_{m}$は入出力には直接関係ないワイヤに割り当てられる値。

素朴な証明プロトコル

$y=F(u)$を多項式にエンコードできたので、それを用いてステートメント「$y,u$は$y=F(u)$を満たす」を証明するプロトコルを考えてみましょう。

はじめに、$\sum_i c_i v_i(x)$などを入出力に関係する部分(i/o)とそうでない部分(mid)に分けておきます。

$$\begin{align} &v_{\mathrm{i/o}}(x):=\sum_{i=1}^{N} c_i v_i(x)\\ &v_{\mathrm{mid}}(x):=\sum_{i=N+1}^{m} c_i v_i(x)\\ &w_{\mathrm{i/o}}(x):=\sum_{i=1}^{N} c_i w_i(x)\\ &w_{\mathrm{mid}}(x):=\sum_{i=N+1}^{m} c_i w_i(x)\\ &y_{\mathrm{i/o}}(x):=\sum_{i=1}^{N} c_i y_i(x)\\ &y_{\mathrm{mid}}(x):=\sum_{i=N+1}^{m} c_i y_i(x) \end{align}$$

セットアップ
ProverとVerifierは$\{v_k(x)\}_{k=0,\ldots,m}$, $\{w_k(x)\}_{k=0,\ldots,m}$, $\{y_k(x)\}_{k=0,\ldots,m}$を共有しておきます。これらの値は$F$に依存しますが、$F$の入出力$u, y$とは関係がないことに注意してください。

証明の作成
Proverは$y=F(u)$を元に$h(x):=p(x)/t(x)$, $v_{\mathrm{mid}}(x), w_{\mathrm{mid}}(x), y_{\mathrm{mid}}(x)$を計算して、$u, y$とともにVerifierに送ります。

検証
Verifierは次の検証を行います。

1. $h(x)$が多項式であること
2. $v_{\mathrm{mid}}(x)$が$\{v_i(x)\}_{i=N+1,\dots,m}$の線形結合であること
3. $w_{\mathrm{mid}}(x)$が$\{w_i(x)\}_{i=N+1,\dots,m}$の線形結合であること
4. $y_{\mathrm{mid}}(x)$が$\{y_i(x)\}_{i=N+1,\dots,m}$の線形結合であること

つぎに$u, y$の値から$v_{\mathrm{i/o}}(x), w_{\mathrm{i/o}}(x), y_{\mathrm{i/o}}(x)$を計算し、

$$p(x) = (v_0(x) + v_{\mathrm{i/o}}(x) + v_{\mathrm{mid}}(x))(w_0(x) + w_{\mathrm{i/o}}(x) + w_{\mathrm{mid}}(x)) - y_0(x) - y_{\mathrm{i/o}}(x) - y_{\mathrm{mid}}(x)$$

を構成します。最終的に

5. $p(x)=h(x)t(x)$であること

を検証します。

これら5つのテスト全てに合格すれば、ステートメント「$y,u$は$y=F(u)$を満たす」を受理します。

1の検証は、$p(x)/t(x)$が割り切れないケースを弾きます。2,3,4は$p(x)$を正しく構成する為に行います。$v_0(x),v_{\mathrm{i/o}}(x)$はVerifierが用意するので問題ありませんが、$v_{\mathrm{mid}}(x)$はProverが提供するので正しく構成されているか確認する必要があるのです。

上記のプロトコルはゼロ知識でも簡潔でもありません。次の節で導入する群やペアリングといった道具を用いて、このプロトコルを簡潔化し、その後にゼロ知識化します。このプロトコルは多項式の恒等式を検証する必要があり、コストが高くなっています。zk-SNARKでは、多項式を扱う代わりに、変数$x$にあるランダムな値$s$を代入し、値として扱うという手法を用います。その手法の正当性を与えるのがSchwartz–Zippelの補題です。また、2,3,4の線形結合かどうかの検証はKC(Knowledge of Coefficient) と呼ばれるテクニックで効率的に行なえます。いずれも、次の節で解説します。

数学的背景

離散対数問題とDH問題

$G$を巡回群、$g$をその生成元とします。$g$は生成元なので、群$G$の任意の元は、ある自然数$n$を用いて$g^n$の形で書くことができます。$g^n$から$n$を求める問題は離散対数問題と呼ばれ、離散対数問題を解く効率的な($\log n$程度の時間の)アルゴリズムは存在しないと考えられています^[3]。

なお、$g$の$n$乗は効率的に($\log n$程度の時間で)計算することができます。例えば$g^{1024}$を計算したい場合、$g^2$をまず計算して, $g^4=(g^2)^2$, $g^{16}=(g^4)^2$...のように2乗を繰り返せば10回の計算で済みます。2のべき乗以外の値も2進数表記すると2のべき乗の組み合わせで書けるので効率的に計算できます。

離散対数問題と同様に、効率的に解けないと考えられている問題としてDH(Diffie-Hellman)問題があります。これは$g^a$と$g^b$から$g^{ab}$を求める問題です。離散対数問題が解けるなら$a, b$を求め$g^{ab}$を計算することができるので、離散対数問題よりも弱い問題ですが、離散対数問題同様に簡単に解けないと考えられています。

準同型ハイディング

$g^a$と$g^b$から$g^{ab}$を作るのは難しい一方で、$g^{a+b}$を作るのは簡単で、単に掛け合わせればいいだけです。$E(x):=g^x$と定義すると、$E$は次の性質を持ちます

• 一方向性
  $E(x)$から$x$を求めることは難しい(離散対数問題の困難性から)

• 単射性
  $E(x)=E(y)$ならば$x=y$

• 準同型性
  $E(x)E(y) = E(x+y)$が成り立つ

$E$は準同型ハイディング(Homomorphic Hiding) と呼ばれます。

多項式の未知の点における評価

いま未知の$s$に対して$E(1), E(s^1), \ldots, E(s^n)$が与えられているとします。$E$の一方向性から$s$を求めることはできません。しかしながら、多項式$P(x):=\sum_i c_i x^i$に対し$E(P(s))$は次のように求めることができます。

$$\begin{align*} E(P(s)) & = g^{P(s)} = g^{\sum_i c_i s^i}= \prod_i (g^{s^i})^{c_i} = \prod_i E(s^i)^{c_i} \end{align*}$$

すなわち、$s$は未知でも$s$における$P(x)$の評価(に$E$を作用させたもの)は求めることができるのです。

ペアリング

$G_1, G_2, G_3$が群であるとき、双線形性を持つ非縮退の写像$e:G_1 \times G_2 \rightarrow G_3$をペアリングと言います。

双線形性^[4]

$$\begin{align*} e(p_1 p_2, q) = e(p_1, q)e(p_2, q)\\ e(p,q_1q_2) = e(p,q_1)e(p, q_2) \end{align*}$$

Pinocchioでは、$G_1=G_2$が巡回群の場合を扱います。$g$を$G_1=G_2$の生成元とすると、

$$e(g^a, g^b)=e(g,g)^{ab}$$

が成り立ちます。この関係式はよく見るとDH問題に似ています。同じ群の上では$a$と$b$を掛け合わせることはDH問題の困難性によりできませんが、別の群$G_3$上においては可能なのです。

準同型ハイディング$E(x)$に関して、次の式が成り立ちます。

$$e(E(ax), E(y)) = e(g^{ax}, g^y) = e(g,g)^{axy}=e(g^x, g^{ay})=e(E(x), E(ay))$$

すなわち、積の係数を左右どちらにも動かすことができます。この性質は、この後紹介するKnowledge of Coefficientと呼ばれるテクニックで重要な役割を果たします。

Schwartz–Zippelの補題

体$\mathbb{F}_p$上の未知の$n$次多項式$f(x)$と$g(x)$が同じか違うかを判定したいとします^[5]。ただし、$p \gg n$とします。正確に判定しようと思うと、全ての$x\in\mathbb{F}_p$に対して$f(x)=g(x)$かどうか調べる必要がありますが、確率的な判定で良いのなら、非常にシンプルでかつ信頼性の高い方法が知られています: ランダムに値$s$を選び$f(s) - g(s)=0$なら「同じ」、$f(s) - g(s)\neq0$なら「違う」と判定するのです。

後者は良いとして、何故前者で「同じ」と判定しても良いのでしょうか？理由は次の通りです。$f(x)-g(x)$は高々$n$次の多項式なので、高々$n$個しか根を持ちません。$\mathbb{F}_p$から運悪く$f(x)-g(x)$の根を引き当てる確率は$n/|\mathbb{F}_p|$ほどで、$p \gg n$のとき無視できるほど小さく、したがって、$f(s) - g(s)=0$なのに$f(x) \neq g(x)$である確率は無視できるほど小さいのです。これをSchwartz–Zippelの補題と言います。

すでに、未知の点$s$において多項式$P(x)$の評価の準同型ハイディング$E(P(s))$について述べました。信頼できる第三者が秘密の$s$をランダムに選び、$E(1), E(s^1), \ldots, E(s^n)$を提供するなら、多項式$P(x)$と$Q(x)$が同じであることの証明は、Schwartz–Zippelの補題を使って次のように行えそうです。

1. Proverは$E(P(s))$と$E(Q(s))$を計算し、Verifierに送る。
2. Verifierは$E(P(s)) = E(Q(s))$かどうかを判定する。

ただし、この方法はProverが正直に$E(P(s))$や$E(Q(s))$を計算したのか判定しようがないのでうまくいきません。次の節で述べるKCのテクニックなどと組み合わせる必要があります。

KC(Knowledge of Coefficient)

$E(s)$と$E(\alpha s)$のように、$E$の中身が$\alpha$倍になっている関係を、「$\alpha$の関係」と呼ぶことにします。

• $E(1)$と$E(\alpha)$
• $E(s)$と$E(\alpha s)$
• $E(s^2)$と$E(\alpha s^2)$

はいずれも「$\alpha$の関係」を持ったペアです。
これら3つのペアから、別の「$\alpha$の関係」を持ったペアを作ることはできるでしょうか？

例えば$E(2)=E(1)E(1)$と$E(2 \alpha)=E(\alpha)E(\alpha)$や、$E(1 + s + s^2)=E(1)E(s)E(s^2)$と、$E(\alpha+\alpha s+\alpha s^2)=E(\alpha)E(\alpha s)E(\alpha s^2)$などは作ることができます。

しかしながら$E(s^3)$と$E(\alpha s^3)$のペアなどは作ることができません。$E(s^3)=E(s^2 \cdot s)$や$E(\alpha s^3)=E(\alpha s^2 \cdot s)$を求めるのは、DH問題の困難性から難しいのです。

以上の考察から、次のことが言えそうです。

主張
$E(1), E(s), E(s^2), E(\alpha),E(\alpha s),E(\alpha s^2)$が既知のとき、ある$p$に対して「$\alpha$の関係」を持ったペア$E(p)$, $E(\alpha p)$を作ることができるなら、その$p$は、ある$c_0, c_1, c_2$を用いて$p = c_0 + c_1 s + c_2 s^2$と書ける。

すなわち別の「$\alpha$の関係」を持ったペアは、既存の「$\alpha$の関係」を持ったペアの線形結合でしか作れないのです。

あるペア$E(x)$, $E(y)$が「$\alpha$の関係」を持っているかどうかはペアリングを用いて検証することができます。

$$e(E(x), E(\alpha)) \overset{?}{=} e(E(y), E(1))$$

このテストに合格すれば$y = \alpha x$、すなわち$E(x)$, $E(y)$は「$\alpha$の関係」を持っていることが分かります。

これらを一般化してProver-Verifierの形で言い直してみます。

主張
$v_1,v_2,\ldots,v_n$と$E(v_1),E(v_2), \ldots,E(v_n)$, $E(\alpha), E(\alpha v_1),E(\alpha v_2), \ldots,E(\alpha v_n)$が既知であるとする^[6]。Proverが「$\alpha$の関係」を持ったペア$E(p)$, $E(\alpha p)$をVerifierに送り、Verifierが$e(E(p), E(\alpha)) \overset{?}{=} e(E(\alpha p), E(1))$を確認したなら、Verifierは$p$が$p = c_0 + \sum_i c_i v_i$の形で書けることを確証できる。

$p$に$c_0$が入っていますが、これは$E(c_0)$と$E(\alpha c_0)=E(\alpha)^{c_0}$が作れることに由来します。$E(\alpha)$が提供されなければこのようなペアを作ることはできませんが、今度はペアリングのテストが行えなくなってしまいます。これは、もう一つの未知値$\beta$を導入して、ペアリングテストで使うものと分離することで解決できます。

主張(改良版)
$v_1,v_2,\ldots,v_n$と$E(v_1),E(v_2), \ldots,E(v_n)$, $E(\beta), E(\alpha \beta), E(\alpha v_1),E(\alpha v_2), \ldots,E(\alpha v_n)$が既知であるとする。Proverが「$\alpha$の関係」を持ったペア$E(p)$, $E(\alpha p)$をVerifierに送り、Verifierが$e(E(p), E(\alpha \beta)) \overset{?}{=} e(E(\alpha p), E(\beta))$を確認したなら、Verifierは$p$が$p = \sum_i c_i v_i$の形で書けることを確証できる。

以上のテクニックをKC(Knowledge of Coefficient)、またこの主張が成り立つという暗号学的な仮定を KCA(Knowledge of Coefficient Assumption) と言います。

Pinocchioプロトコルの詳細

Schwartz–Zippelの補題を用いて、先程の「素朴な証明プロトコル」における多項式を、ランダムな点$s$で評価しましょう。すると、最初の4つの検証は次のようになります。

1. $h(s)$が$s$の多項式であること
2. $v_{\mathrm{mid}}(s)$が$\{v_i(s)\}_{i=N+1,\dots,m}$の線形結合であること
3. $w_{\mathrm{mid}}(s)$が$\{w_i(s)\}_{i=N+1,\dots,m}$の線形結合であること
4. $y_{\mathrm{mid}}(s)$が$\{y_i(s)\}_{i=N+1,\dots,m}$の線形結合であること

$h(s)$が多項式であるとは、$h(s)$が$1, s, s^2, \ldots$の線形結合であることと同値であり、KCのテクニックで証明することができます。2,3,4も同様にKCのテクニックで証明することができます。

$p(s)=h(s)t(s)$であることの検証もSchwartz–Zippelの補題とペアリングを用いて、

$$e(E(p(s)), E(1)) \overset{?}{=} e(E(h(s)), E(t(s)))$$

とすれば良いことが分かります。以上より、次のようなPinocchioプロトコルを構成することができます。

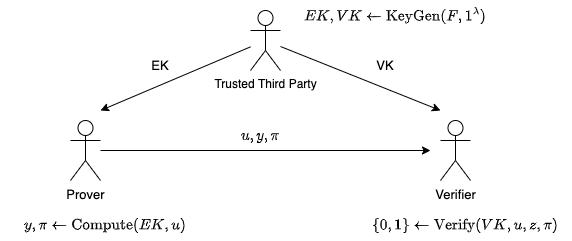Pinocchioプロトコルの流れ(再掲)

トラステッドセットアップ

$d$を$v_k(x),w_k(x),y_k(x)$の最高の次元とします。 $I_{\mathrm{i/o}}:=\{1,\ldots,N\}$, $I_{\mathrm{mid}}:=\{N,\ldots,m\}$, $[d]:=\{1,2,\ldots,d\}$と表記します。

信頼できる第三者は、$s, \alpha, \beta_v, \beta_w, \beta_y, \gamma$をランダムに選び、

評価鍵

$$EK = \{\{E(s^i)\}_{i\in [d]}, \{E(\alpha s^i)\}_{i\in [d]}, \{E(v_i(s))\}_{i\in I_{\mathrm{mid}}}, \{E(w_i(s))\}_{i\in I_{\mathrm{mid}}}, \{E(y_i(s))\}_{i\in I_{\mathrm{mid}}}, \{E(\beta_v v_i(s))\}_{i\in I_{\mathrm{mid}}}, \{E(\beta_w w_i(s))\}_{i\in I_{\mathrm{mid}}}, \{E(\beta_y y_i(s))\}_{i\in I_{\mathrm{mid}}} \}$$

検証鍵

$$VK = \{E(1), E(\alpha), E(\gamma),E(\beta_v \gamma),E(\beta_w \gamma),E(\beta_y \gamma), E(t(s)), E(v_0(s)),E(w_0(s)),E(y_0(s)), \{E(v_i(s))\}_{i\in I_{\mathrm{i/o}}}, \{E(w_i(s))\}_{i\in I_{\mathrm{i/o}}}, \{E(y_i(s))\}_{i \in I_{\mathrm{i/o}}} \}$$

を作成し公表します。$s, \alpha, \beta_v, \beta_w, \beta_y, \gamma$は破棄します。

プルーフの作成

Proverは$y=F(u)$に対応する回路の値割り当て$\{c_i\}$を作成し、
$E(v_{\mathrm{mid}}(s)), E(\beta_v v_{\mathrm{mid}}(s))$を次のように構成します。

$$\begin{align*} &E(v_{\mathrm{mid}}(s)) = \prod_{i \in I_{\mathrm{mid}}} E(v_i(s))^{c_i}\\ &E(\beta_v v_{\mathrm{mid}}(s)) = \prod_{i \in I_{\mathrm{mid}}} E(\beta_v v_i(s))^{c_i} \end{align*}$$

$E(w_{\mathrm{mid}}(s)), E(\beta_w w_{\mathrm{mid}}(s)), E(y_{\mathrm{mid}}(s)), E(\beta_y y_{\mathrm{mid}}(s))$についても同様に構成します。

次に、

$$\begin{align*} & p(x) := \left(v_0(x) + \sum_{i=1}^{m} c_i v_i(x) \right)\left(w_0(x) +\sum_{i=1}^{m} c_i w_i(x) \right) -y_0 - \sum_{i=1}^{m} c_i y_i(x)\\ & h(x) := p(x)/t(x) \end{align*}$$

を計算します。多項式$h(x)$の係数を$\{h_i\}$とすると、$E(h(s))$と$E(\alpha h(s))$は次のように構成できます。

$$\begin{align*} &E(h(s)) = \prod_{i \in [d]} E(s^i)^{h_i}\\ &E(\alpha h(s)) = \prod_{i \in [d]} E(\alpha s^i)^{h_i}\\ \end{align*}$$

これらをまとめてプルーフ

$$\pi = \{ E(v_{\mathrm{mid}}(s)),E(w_{\mathrm{mid}}(s)),E(y_{\mathrm{mid}}(s)),E(h(s)), E(\alpha h(s)), E(\beta_v v_{\mathrm{mid}}(s)),E(\beta_w w_{\mathrm{mid}}(s)),E(\beta_y y_{\mathrm{mid}}(s)) \}$$

を作成し$u, y$とともにVerifierに送ります。

検証

Verifierは検証鍵$VK$を用いてプルーフ$\pi$を次のように検証します。

$$\begin{align*} &e(E(\alpha h(s)), E(1)) \overset{?}{=} e(E(h(s)), E(\alpha))\\ &e(E(\beta_v v_{\mathrm{mid}}(s)), E(\gamma)) \overset{?}{=} e(E(v_{\mathrm{mid}}(s)), E(\beta_v \gamma))\\ &e(E(\beta_w w_{\mathrm{mid}}(s)), E(\gamma)) \overset{?}{=} e(E(w_{\mathrm{mid}}(s)), E(\beta_w \gamma))\\ &e(E(\beta_y v_{\mathrm{mid}}(s)), E(\gamma)) \overset{?}{=} e(E(y_{\mathrm{mid}}(s)), E(\beta_y \gamma)) \end{align*}$$

第1式によって$h(s)$が多項式であることが分かり、第2,3,4式によって$v_{\mathrm{mid}}(s)$, $w_{\mathrm{mid}}(s)$, $y_{\mathrm{mid}}(s)$がそれぞれ$\{v_i(s)\}_{i \in I_{\mathrm{mid}}}$, $\{w_i(s)\}_{i \in I_{\mathrm{mid}}}$, $\{y_i(s)\}_{i \in I_{\mathrm{mid}}}$の線形結合であることが分かります。

$u,y$($=\{c_i\}_{i \in I_{\mathrm{i/o}}}$)を用いて、

$$\begin{align*} E(v_{\mathrm{i/o}}(s)) = \prod_{i \in I_{\mathrm{i/o}}} E(v_i(s))^{c_i}\\ E(w_{\mathrm{i/o}}(s)) = \prod_{i \in I_{\mathrm{i/o}}} E(w_i(s))^{c_i}\\ E(y_{\mathrm{i/o}}(s)) = \prod_{i \in I_{\mathrm{i/o}}} E(y_i(s))^{c_i}\\ \end{align*}$$

を計算し、$p(s) \overset{?}{=} h(s)t(s)$の検証を行います。

$$\begin{align*} &v_e := E(v_0(s))E(v_{\mathrm{i/o}}(s))E(v_{\mathrm{mid}}(s))\\ &w_e := E(w_0(s))E(w_{\mathrm{i/o}}(s))E(w_{\mathrm{mid}}(s))\\ &y_e := E(y_0(s))E(y_{\mathrm{i/o}}(s))E(y_{\mathrm{mid}}(s))\\ &\frac{e(v_e,w_e)}{e(y_e, E(1))} \overset{?}{=} e(E(h(s)), E(t(s))) \end{align*}$$

以上のテスト全てに合格すれば、ステートメント「$u$, $y$は$y=F(u)$を満たす」を受理します。

このプロトコルはsuccinctです。プルーフは８個の$G$の元であり、定数サイズです。また、検証に必要な計算量も、$N$($F$の入力変数、出力変数の合計数)のオーダーであり^[7]、$F(u)$の計算量に依存しません。

ゼロ知識化

入力変数$c_i$を秘密にしたい場合、インデックス$i$を$I_{\mathrm{i/o}}$から$I_{\mathrm{mid}}$へ移すだけで、ある程度秘匿化されます(プルーフから$c_i$を求めることが難しくなります)。

しかしながら、少し手を加えるだけで、完全にゼロ知識化することもできます。

Proverはランダムな$\delta_v, \delta_w, \delta_y$を選び、

$$\begin{align*} &v_{\mathrm{mid}}(x):=\sum_{i\in I_{\mathrm{mid}}} c_i v_i(x) + \delta_v t(s) \\ &w_{\mathrm{mid}}(x):=\sum_{i\in I_{\mathrm{mid}}} c_i w_i(x) + \delta_w t(s)\\ &y_{\mathrm{mid}}(x):=\sum_{i\in I_{\mathrm{mid}}} c_i y_i(x) + \delta_y t(s) \end{align*}$$

と変更します(それに合わせて$p(x), h(x)$も変更します)。

このように変更しても、やはり$p(s)$は$t(s)$で割り切れるのでVerifier側の手順は全く変わりません。$\delta_v, \delta_w, \delta_y$を完全にランダムに選べば、$v_{\mathrm{mid}}(s)$などは$\{c_i\}_{i\in I_{\mathrm{mid}}}$と相関しなくなります。

以上よりzk-SNARKなプロトコルを構成することができました。

最後に

この記事の内容はPinocchioプロトコルの原論文のセクション2までに対応します(わかりやすさを優先して、少し変更した部分もあります)。セクション3以降では更に工夫を加えて効率化したバージョンも紹介されていますが、今回は取り上げませんでした。

この記事の間違い等にお気づきになった方や、ご質問がある方は、twitterのDMまでお気軽にご連絡ください。

参考にした記事

https://eprint.iacr.org/2013/279

https://zenn.dev/kyosuke/articles/a1854b9be26c01df13eb

https://leonahioki.medium.com/楕円曲線の夢の国に住もう-12dcc675995a

Why and How zk-SNARK Works:

• Why and How zk-SNARK Works 1: Introduction & the Medium of a Proof
• Why and How zk-SNARK Works 2: Proving Knowledge of a Polynomial
• Why and How zk-SNARK Works 3: Non-interactivity & Distributed Setup
• Why and How zk-SNARK Works 4: General-Purpose Computation
• Why and How zk-SNARK Works 5: Variable Polynomials
• Why and How zk-SNARK Works 6: Verifiable Computation Protocol
  
• Why and How zk-SNARK Works 7: Constraints and Public Inputs
• Why and How zk-SNARK Works 8: Zero-Knowledge Computation

Electric Coin blog series:

• Explaining SNARKs Part I: Homomorphic Hidings
• Explaining SNARKs Part II: Blind Evaluation of Polynomials
• Explaining SNARKs Part III: The Knowledge of Coefficient Test and Assumption
• Explaining SNARKs Part IV: How to make Blind Evaluation of Polynomials Verifiable
• Explaining SNARKs Part V: From Computations to Polynomials
• Explaining SNARKs Part VI: The Pinocchio Protocol
• Explaining SNARKs Part VII: Pairings of Elliptic Curves

脚注

1. argument(論拠, 根拠)の類義語にproof(証明)があります。ゼロ知識証明の文脈では、proofは偽造しようのない証拠、argumentは非常に長い計算時間(例えば、指数関数時間)をかければ偽造できる証拠を意味します。すなわち、argumentは計算量的仮定が必要なproofという意味で使われています。ただし、Pinocchioの原論文でもargumentの意味でproofが使われている箇所があるので、あまり厳密に区別するものでもないのかもしれません。この記事でも以降はargumentとproofは同一の意味で使っています。

2. ただし、proofの作成は$f(x, y)$の計算より多くの計算が必要なので、Proverも含めた全体の計算コストはむしろ増えます。

3. 量子コンピューターを使うと離散対数問題が効率的に解けることが知られています。

4. 今回は$G_1$, $G_2$の演算を積として表記したので、「双線形」っぽくないですが、本来の文脈では$G_1$,$G_2$は楕円曲線上の点の和に関する群なので$e(p_1+p_2, q) = e(p_1, q)e(p_2, q)$などとなり、「双線形」がしっくりきます。

5. $f(x),g(x)$は未知なので直接係数を比較したりはできませんが、$x$を入力すると$f(x),g(x)$を出力するクエリは利用できるものとします

6. $v_i$から$E(v_i)$が作れるので$E(v_i)$は不要ですが、わかりやすさの為に残しています

7. このプロコトルでは$v_{\mathrm{i/o}}(s)$, $w_{\mathrm{i/o}}(s)$, $y_{\mathrm{i/o}}(s)$を計算するのに$3N$回の計算が必要ですが、入出力を全て左ワイヤ、すなわち$v_{\mathrm{i/o}}(s)$に押し付けると$N$回の計算で済みます(原論文ではそちらの手法が取られています)。