proto-danksharding(EIP-4844)の概要
proto-danksharding (EIP-4844)とは、Ethereumにshard blob transactionと呼ばれる新しいトランザクション形式を追加する提案です。shard blob transactionはblobと呼ばれる新しい形式のデータを持っているトランザクションで、大きなデータをEthereumに安価に公開するために利用できます。
また、EIP-4844はEthereumのスケーラビリティを大幅に向上させるdankshardingと呼ばれる構想に向けた最初のステップという側面もあります。
モチベーション
EIP-4844はrollupのための技術です。
Rollupとはoff chainの取引データを効率よく圧縮してEthereumで検証することで、Ethereumと同等のセキュリティを保ちながら安価な取引手数料を実現するスケーリングソリューションです。
Rollupは取引データの検証方式が異議申し立て方式に基づくoptimistic rollupと、ゼロ知識証明に基づくzkrollupに大別できますが、いずれにしても取引データをEthereum上に公開する必要があります。これは取引データが利用できなくなってしまうと
- optimistic rollupの場合は異議申し立てができずに資産が盗まれる
- zkrollupの場合は新しくゼロ知識証明が作れず資産がロックされる
という問題が発生するためです(data availability problem)。現状は最も安価なcalldataと呼ばれる形式で取引データが公開されているのですが、それでもまだ高価であるという問題があります。
EIP-4844はcalldataよりもより安価に利用できるblobと呼ばれるデータ形式を導入することで、この問題を緩和できると考えられています。
blobとは
blobは
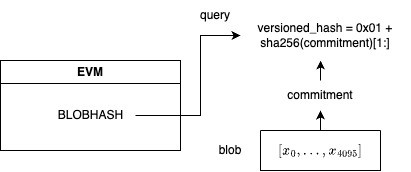
EVMからblobの中身を直接読み取ることはできません。代わりにversioned_hashと呼ばれる256bitの値にアクセスできます。
versioned_hashはblobのcommitment(後に説明します)のハッシュを取ったものに、バージョン情報0x01を添付したものです。現在バージョンは0x01しかありませんが、今後異なるcommitmentスキームが導入された場合はこの値を変えて表現します。
EVMはBLOBHASHというopcodeでトランザクションが持っているblobのversioned_hashを取得することができます。
blobのgas fee
blobはEVMのfee marketとは独立したfee marketを持ちます。つまり、EIP-4844導入後は2つの独立したfee marketが存在することになります。
既存のgasと区別するために、blobに関するgasをdata gasと呼ぶことにします。
1つのblobは2**17data gasを消費します。1ブロックあたりの目標ガスはTARGET_DATA_GAS_PER_BLOCK = 3*(2**17)に設定されています。これは1 blockに3 blob未満なら次ブロックのdata gas priceは下がり、4 blob以上なら上がることを意味します。また1ブロックの最大ガスはMAX_DATA_GAS_PER_BLOCK = 6*(2**17)に設定されており、最大で6個のblobが入ります。
calldataと比較して具体的にどれほど安くなるかは、EIP-4844が導入され市場原理でgas priceが決まるまでわかりませんが、calldataと比べ用途が限定的なので、特に最初のうちは安価になると考えられます。
EIP-4844で導入されるprecompile contract
precompile contractとは、プロトコルで定められた固定のaddressを持つ、固有の機能が実装されたcontractのことです。EIP-4844ではaddress0x0Aを持つpoint evaluation precompileと呼ばれるものが導入されます。
その前に、EIP-4844で利用されているコミットメント(KZG commitment)について概要を解説します。
blobは
多項式
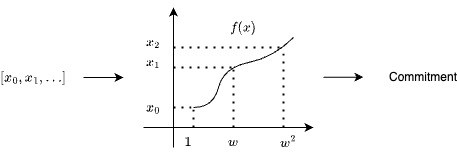
ある整数
公開情報をKZG commitmentと整数proofを検証者がチェックすることで、検証者が
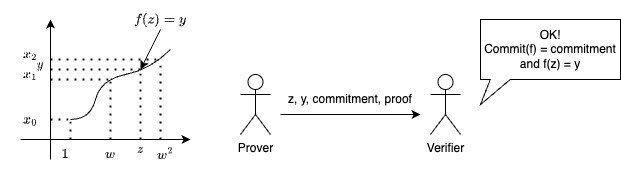
この検証者の役割を担うのがpoint evaluation precompileです。point evaluation precompileはversioned_hash, z, y, commitment, proofを連結した入力を受け取り、検証に成功した場合はFIELD_ELEMENTS_PER_BLOB (4096)とBLS_MODULUS(p)を連結した値を返します。
point evaluation precompileの使用用途
point evaluation precompileを利用してversioned_hashに対応するblobのversioned_hashにしかアクセスできませんが、point evaluation precompileを使うとblobの中身をEVMに対して証明することができるのです。blob transaction内でこれを使うこともできますし、blob transactionではversioned_hashをストレージに保存する処理のみ行っておき、しばらく後の通常のtransactionでblobの内容を証明することもできます。
また、同じ
なお、KGZ commitmentやKate proofの詳細は次の記事がおすすめです。
なぜblobなのか?
なぜcalldataなどの既存のデータ領域を増やすのではなく、わざわざblobのようなデータ形式を導入するのでしょうか?
いくつかの理由があります。
最大ブロックサイズが大きくなりすぎない
calldataのgasを安くすると、calldataが大部分を占めるブロックが生成された場合、ブロックのサイズが大きくなりすぎてしまいます。大きいブロックはネットワークでの伝搬が間に合わず、コンセンサスの失敗を引き起こす可能性があります。blobは1ブロックあたりの最大数が決まっており、ワーストケースでもブロックサイズが大きくなりすぎることはないのでこの問題が発生しません。
一定期間後に消去できる
blob本体はEVMからアクセスできないため、コンセンサスが終わればblob本体は不要になります。そのため、blobは一定期間(典型的には18日)後に消去することができます。
point evaluationができる
point evaluation precompileによってblobの中身を効率的に証明したり、zk-SANRKsと組み合わせることができます。
DAS(data availability sampling)と相性が良い
DAS(data availability sampling)とは、blobがダウンロード可能なことをblob全てをダウンロードせずに確認する技術です[4]。EIP-4844ではDASは実装されませんが、将来的にはDASによってblobの検証が高速化されます。blobを現在の段階で採用することで、DASをスムーズに導入できます。
参考文献
-
これは演算を有限体
\mathbb{F}_p -
一般的に
n n-1 n=1 f n=2 f -
詳しくは https://ethresear.ch/t/easy-proof-of-equivalence-between-multiple-polynomial-commitment-schemes-to-the-same-data/8188 ↩︎
-
詳しくは https://a16zcrypto.com/posts/article/an-overview-of-danksharding-and-a-proposal-for-improvement-of-das/ ↩︎
Discussion