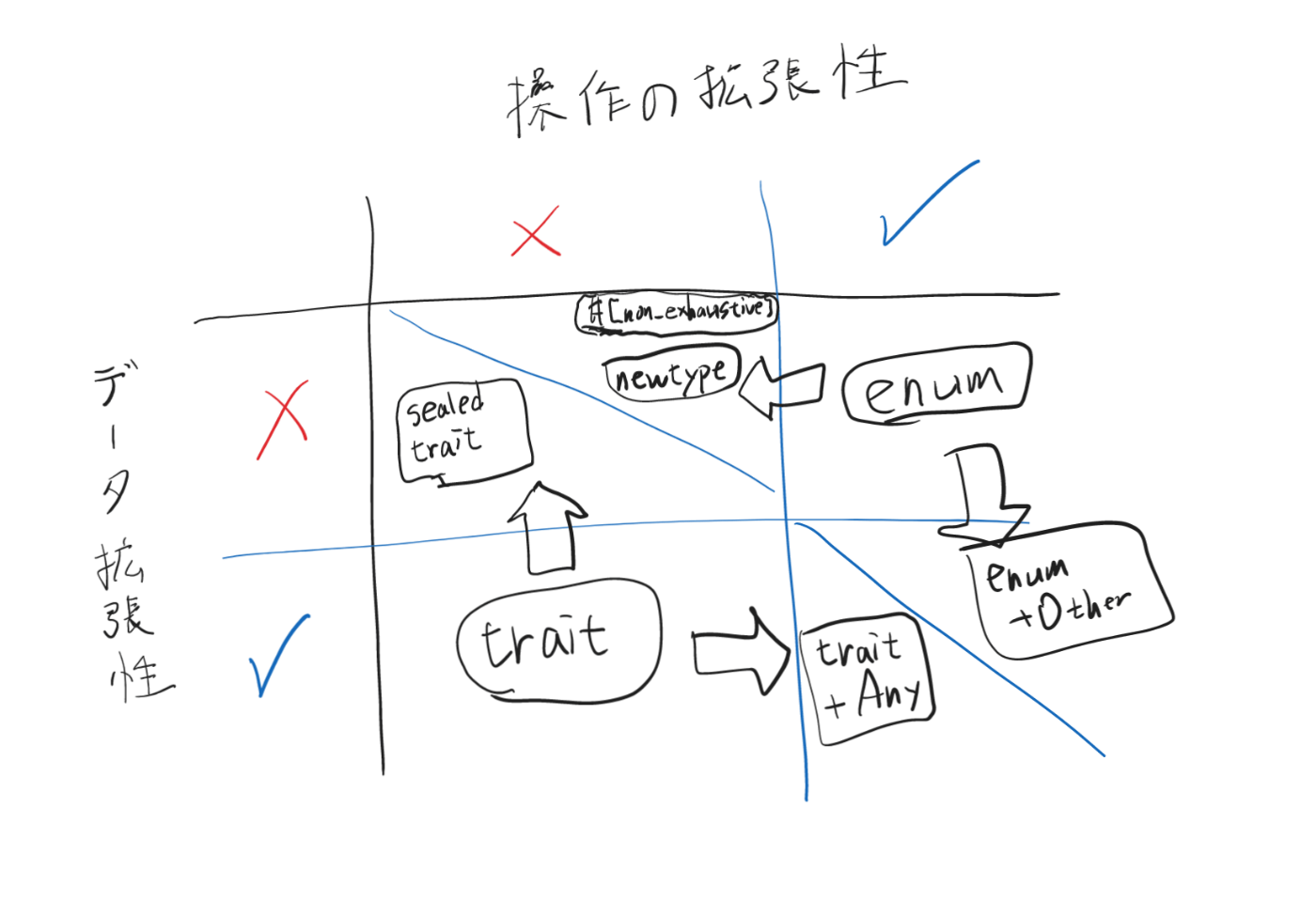
enumはクローズド直和、traitはオープン直和

本稿では直和による多態性を実現する2つの機能、enumとtraitを拡張性の観点から比較します。

→ Expression problem

※enumとtraitを使い分けるにあたってはパフォーマンス要件など他の条件も考慮するべきですが、本記事は多態性の観点のみ説明します。

数式 — enumによる例

本稿では数式をあらわすデータ型を例として扱います。enumではこのように定義されます。

#[derive(Debug)]
pub enum Expr {
    Var(String),
    Add(Box<Expr>, Box<Expr>),
    Sub(Box<Expr>, Box<Expr>),
    Mul(Box<Expr>, Box<Expr>),
    Div(Box<Expr>, Box<Expr>),
}

数式の評価は以下のように行えます。

impl Expr {
    pub fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        match self {
            Expr::Var(name) => vars[name],
            Expr::Add(lhs, rhs) => lhs.eval(vars) + rhs.eval(vars),
            Expr::Sub(lhs, rhs) => lhs.eval(vars) - rhs.eval(vars),
            Expr::Mul(lhs, rhs) => lhs.eval(vars) * rhs.eval(vars),
            Expr::Div(lhs, rhs) => lhs.eval(vars) / rhs.eval(vars),
        }
    }
}

数式 — traitによる例

一方、数式をtraitで定義することも可能です。この場合以下のようにevalをtraitの一部に含めることになります。

pub trait Expr: Debug {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64;
}

#[derive(Debug)]
pub struct VarExpr(String);
impl Expr for VarExpr {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        vars[&self.0]
    }
}

#[derive(Debug)]
pub struct AddExpr(Box<dyn Expr>, Box<dyn Expr>);
impl Expr for AddExpr {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        self.0.eval(vars) + self.1.eval(vars)
    }
}

#[derive(Debug)]
pub struct SubExpr(Box<dyn Expr>, Box<dyn Expr>);
impl Expr for SubExpr {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        self.0.eval(vars) - self.1.eval(vars)
    }
}

#[derive(Debug)]
pub struct MulExpr(Box<dyn Expr>, Box<dyn Expr>);
impl Expr for MulExpr {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        self.0.eval(vars) * self.1.eval(vars)
    }
}

#[derive(Debug)]
pub struct DivExpr(Box<dyn Expr>, Box<dyn Expr>);
impl Expr for DivExpr {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        self.0.eval(vars) / self.1.eval(vars)
    }
}

データ拡張性

定義した数式型に対して、利用側で拡張を加えることを考えます。

たとえば、「加減乗除のほかに、 $exp(x)$ という式を追加する」ということを考えます。これができるのはExprをtraitで定義した場合です。

// exp(x) のための式を追加で定義
#[derive(Debug)]
pub struct ExpExpr(Box<dyn Expr>);
impl Expr for ExpExpr {
    fn eval(&self, vars: &HashMap<String, f64>) -> f64 {
        self.0.eval(vars).exp()
    }
}

一方enumの場合は定義した時点で可能なパターンが確定するようになっており、拡張性はありません。

操作の拡張性

今度は、「数式の値そのものではなく、ある地点での偏微分を (記号的に) 計算する」ということを考えます。これができるのはExprをenumで定義した場合です。

// 式の値と偏微分を計算する
pub fn pdiff(e: &Expr, vars: &HashMap<String, f64>, d: &str) -> (f64, f64) {
    match e {
        Expr::Var(name) if name == d => (vars[name], 1.0),
        Expr::Var(name) => (vars[name], 0.0),
        Expr::Add(lhs, rhs) => {
            let (lv, ld) = pdiff(lhs, vars, d);
            let (rv, rd) = pdiff(rhs, vars, d);
            (lv + rv, ld + rd)
        }
        Expr::Sub(lhs, rhs) => {
            let (lv, ld) = pdiff(lhs, vars, d);
            let (rv, rd) = pdiff(rhs, vars, d);
            (lv - rv, ld - rd)
        }
        Expr::Mul(lhs, rhs) => {
            let (lv, ld) = pdiff(lhs, vars, d);
            let (rv, rd) = pdiff(rhs, vars, d);
            (lv * rv, ld * rv + lv * rd)
        }
        Expr::Div(lhs, rhs) => {
            let (lv, ld) = pdiff(lhs, vars, d);
            let (rv, rd) = pdiff(rhs, vars, d);
            (lv / rv, (ld * rv - lv * rd) / (rv * rv))
        }
    }
}

traitの場合、デフォルトではダウンキャストできないため、式の内容に応じて分岐することはできません。そのため、既知の操作である Expr::eval で表現できる操作以外は実現できません。

データと操作を同時に拡張する

データと操作を同時に拡張するには、「拡張操作を拡張データに対して適用したらどうなるか？」を考える必要があります。

上の例の場合、

• $exp(x)$ を新たな式として追加する
• 偏微分を新たな操作として追加する

がどちらも行えたとすると、 $exp(x)$ の偏微分を誰も定義しない という問題が起きます。

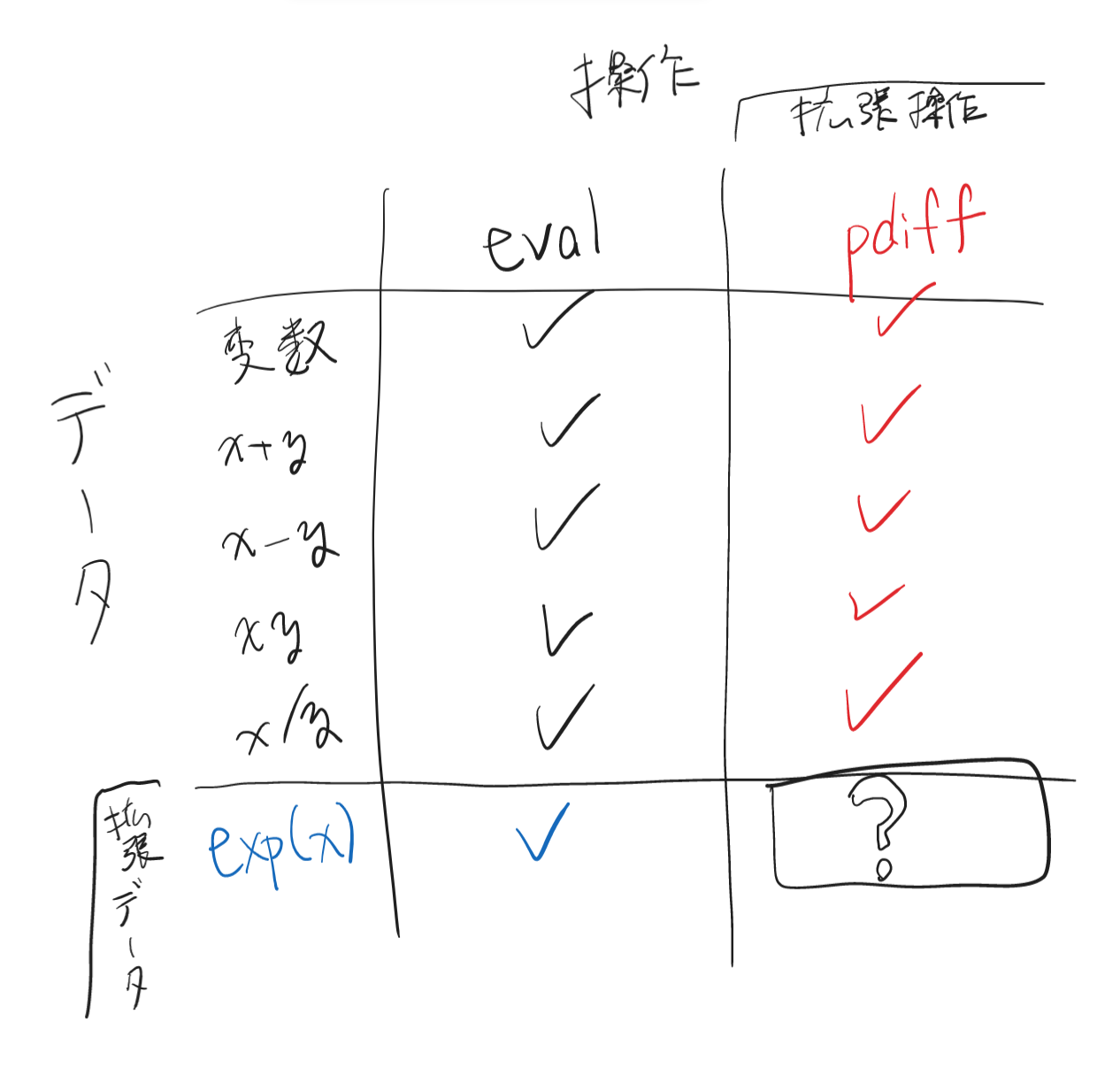
データと操作を同時に拡張する — enumベース

enumベースでデータを拡張可能にするには、trait objectを入れられる分岐を足すのが一般的です。

#[derive(Debug)]
pub enum Expr {
    Var(String),
    Add(Box<Expr>, Box<Expr>),
    Sub(Box<Expr>, Box<Expr>),
    Mul(Box<Expr>, Box<Expr>),
    Div(Box<Expr>, Box<Expr>),
    Other(Box<dyn ExprTrait>),
}

この場合、未知のデータのハンドリング方法は拡張操作の実装側で決定することになります。

データと操作を同時に拡張する — traitベース

traitに Any を継承させると、具象型へのダウンキャストが使えるようになります。これを使うことで、trait objectが既知の型に由来する場合を判別して異なる実装を与えることができます。

ダウンキャストには以下のような注意点があります。

• 'static を仮定する必要がある。
  • 一見すると Any<'a> のようなtraitを作ればいいように思えますが、実はこれには問題があります。 'b: 'a, 'c: 'a のとき、 &'b T: Any<'a> と &'c T: Any<'a> がどちらも成立してしまい、 &'b T と &'c T が ('b と 'c の関係が不明であるにもかかわらず) Any<'a> を経由して相互に変換できてしまいます。
• trait-to-trait downcastingにはより複雑な仕組みが必要。

たとえばstd::error::Errorはダウンキャストを可能にしています。

拡張性を塞ぐ

逆に、データの拡張性と操作の拡張性の両方を塞ぎたい場合も、enumベースとtraitベースの両方のアプローチがあります。

enumベースの場合は以下の2つの方法がよく使われます。

• 網羅性のみを保護する。これには #[doc(hidden)] でマークされたダミーの分岐を足すか、 #[non_exhaustive] 属性をつける方法が使われます。
  • これにより、「将来のマイナーバージョンアップ」でのデータ拡張の余地を残すことができます。
• enumの分岐全体を隠蔽する。
  • Rustの場合、enum自体は可視性制御の仕組みを持たないため、enumをラップしたstructを公開するのが一般的です。

traitベースの場合は、sealed traitパターンが使われます。

structを拡張する

本稿では既存の型に対して新たな分岐を足す問題 (オープン直和) を扱いましたが、これとは別に既存の型に対して新たなフィールドを足す問題 (オープン直積) も考えられます。

これは通常 HashMap<TypeId, Box<dyn Any>> を使って実現されます。たとえばhttpクレートのRequestはextensionsというフィールドが拡張可能フィールドとして提供されています。

まとめ

• enumはクローズド直和、traitはオープン直和である。つまり、traitであれば利用側からデータの選択肢を増やせる。
• 逆に、enumは振る舞いの追加に対してオープンであり、traitは振る舞いの追加に対してクローズドである。
• 両方の拡張を両立するには妥協が必要となる。