【Pytorch】SONYのSQ-VAEを実装する+3次元画像に対応
この記事では,SONYが2022年に開発した深層学習モデルのSQ-VAEについて,
- ざっくりとした動作原理の確認
- 3次元画像に対応した形での実装と簡易的な実験
を,駆け足で行っていきます.
こちらは ラクス Advent Calender 2023 24日目の記事になります。
Introduction:AE族について
ここに,中間のところが細くすぼまった,砂時計の形をした機械があるとします.画像を投げ入れると,細いところを通れるように画像を変形し,そしてまた元の画像の大きさに復元してくれます.
ものすごく細いところを通っているのに,入れた画像と出てきた画像がものすごく似ていたとしたら,細いところを通過しているのは,画像の特徴をものすごくうまく凝縮した,画像のエッセンスであると言えます.
砂時計の上半分だけを使えば,高性能な圧縮マシーンとして使えるということです.
さらには,それっぽいエッセンスを人間が用意して,砂時計の下半分に投入すると,新しいそれっぽい画像を生成するという使い方もできます.巷の生成モデルの原理もおおよそこれにあたります.

以降では砂時計の上半分をエンコーダ,下半分をデコーダと呼ぶことにします.
おおまかにAE(オートエンコーダ)族とグルーピングされる深層学習モデルたちは,基本的にこのようなエンコーダ-デコーダ構造をとっており,SQ-VAEもそのうちのひとつになります.
次節からは,SQ-VAEのコアとなるGumbel-Softmax Relaxationについて説明します.
import and setup
!pip install -q lightning monai
import math
from pathlib import Path
from lightning.pytorch.loggers import CSVLogger
import matplotlib.pyplot as plt
import monai
import numpy as np
import pandas as pd
import pytorch_lightning as pl
from scipy.special import softmax
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data.dataset import Subset
from torchvision import datasets, transforms
mnist_dataset = datasets.MNIST(
root='./data', train=True, transform=transforms.ToTensor(), download=True)
cifar_dataset = datasets.CIFAR10(
root='./data', train=True, transform=transforms.ToTensor(), download=True)
SQ-VAE vs. VQ-VAE
AEの変種のうちの1つであるVQ-VAEは,エンコーダの出力した連続値をargmax関数によって一度完全に離散化するプロセスを踏むため,微分不可能になり,Stop Gradient Operator(離散化のプロセスを完全にスキップして,デコーダからエンコーダへ逆伝播のパスを直接繋げてしまう)を間に噛ませるなどのヒューリスティックが必要でした.
また,VQ-VAEでは,エンコーダの出力がどのコードベクトルへ離散化されるかは,距離に基づいた決定論的なプロセスでした.下図の一番左のボロノイ図に見るように,エンコーダから出力された

https://youtu.be/LARyoWw4Mp8 より引用
それに対し,SQ-VAEは,完全に離散化はせず,Gumbel-Softmax Relaxationという手法を使います.詳細は後述しますが,これは,確率的にコードベクトルを選んでいるとみなすことができるものであり,離れたところにあるコードベクトルにも選ばれるチャンスが生まれます(上図中央).
さらに,微分可能な形でカテゴリカル分布を近似してデコーダへ出力しているため,下図からもわかる通り,逆伝播のパスは途切れません.
 https://www.slideshare.net/thinkingfactory/pr12-categorical-reparameterization-with-gumbel-softmax より引用
https://www.slideshare.net/thinkingfactory/pr12-categorical-reparameterization-with-gumbel-softmax より引用
図中の式における
標準ガンベル分布に従う乱数をシミュレートすると以下のような分布になります.モードは0で,右に裾が長く,-2や4といった値もそこまで珍しくないことが見てとれます.
plot Gumbel
# Random samples from Gumbel(0,1)
eps = 1e-10
U = torch.rand(100000)
g = -torch.log(-torch.log(U + eps) + eps)
plt.hist(g, bins=100)
plt.xlabel('value')
plt.ylabel('count')
plt.title(f'{len(U)} samples from Gumbel(0,1)')
plt.show()

VQ-VAEに比べ,SQ-VAEでは,Gumbel-Softmax Relaxationというたった一手によって、
- 誤差逆伝播のためのヒューリスティックの解消
- 使われないコードベクトルがあった場合のコードブックリセットが不要
- ハイパーパラメータ調整地獄からの解放
という3点について一石三鳥を成し遂げています.
Gumbel-Softmax Relaxationを制御するための2つのパラメータ
Gumbel-Softmax Relaxationが常に一定程度のランダム性を持った挙動をしてしまうと,エンコーダとデコーダは自分のアウトプットに対する正確な評価を得られず,いつまでも学習が収束しないことになります.
そこで,ランダム性を制御するために,「温度」と「param_q」という2つのパラメータが導入されています.
温度(アニーリング)
Gumbel-Softmax Relaxationの計算に登場する
温度は学習におけるその時点のstep数を用いて以下のように計算されます:
ここで,
においては,
なので,
例えば,
plot temperature
# Scheduled temperature decay
temperature_init = 1
decay = 0.01
temperature_min = 0
steps = np.arange(0, 1000, 1)
temperature_step = np.clip(
a=temperature_init * np.exp(-decay * steps),
a_max=None, a_min=temperature_min
)
fig, ax = plt.subplots()
ax.plot(steps, temperature_step)
ax.set_xlabel('step')
ax.set_ylabel('temperature')
ax.set_title(
f'Scheduled temperature decay (init={temperature_init}, decay={decay})'
)
plt.show()
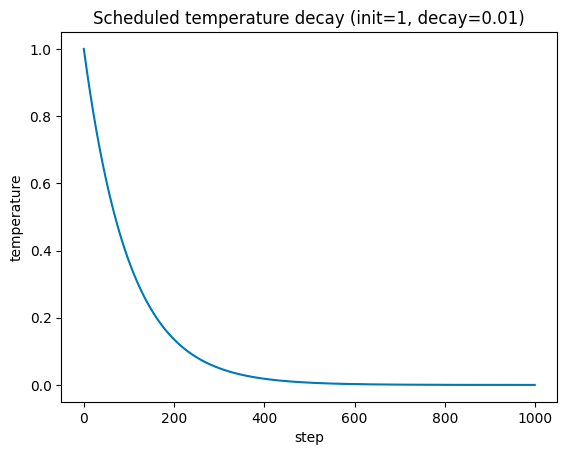
温度が低下する速度は
を使用した場合,
温度は,Gumbel-Softmax Relaxationにおいて,softmax関数への入力ロジットを除算するのに使われています.以下では,通常のsoftmax関数,温度付きsoftmax関数,Gumbel-Softmax Relaxationの順に説明を進めます.
通常のsoftmax関数
以下では簡単のため,softmax関数で2値分類を扱うことを考えますが,容易に多クラス分類へ一般化できます.
クラス0,クラス1それぞれに対するロジットを
通常のsoftmax関数は,2値分類であれば,
と定義されます.
例えば,クラス0,クラス1それぞれに対するロジットが
だったとします.そのままsoftmaxをすれば,それぞれのクラスへの所属確率は
となり,クラス1へ割り当てられる確率は0.6と,そこまで高くありません.
温度付きsoftmax関数
しかし,ここで,softmaxへの入力ロジットを温度で除算するということを考えます.
ロジットを1で割るぶんには変化はないですが,0に近い温度で除算するにつれ,softmaxの結果は極端になっていき,クラス1が圧倒するようになります.
ロジットを(-0.916, -0.511)に固定したまま,温度を1から0へ徐々に変化させ,softmaxの結果を可視化してみます.
plot softmax with temperature
# Impact of temperature on softmax
sample_logit = np.array([-0.916, -0.511])
probabilities = np.array(
[softmax(sample_logit / temperature) for temperature in temperature_step]
)
fig, ax = plt.subplots()
ax.fill_between(
x=temperature_step, y1=probabilities[:, 1], y2=1,
alpha=0.5, label='probability of class 0'
)
ax.fill_between(
x=temperature_step, y1=0, y2=probabilities[:, 1],
alpha=0.5, label='probability of class 1'
)
ax.invert_xaxis()
ax.set_xlabel('temperature')
ax.set_ylabel('probability')
ax.legend(loc='center right')
ax.set_title(f'softmax({sample_logit} / temperature)')
ax.grid()
plt.show()
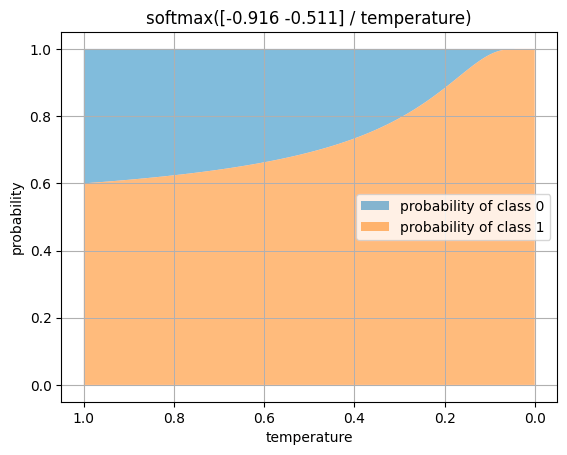
温度が低下するにつれ,元のロジットにおけるわずか0.4の差が大げさに扱われるように変化していく様子がわかります.温度が0.2を下回った時点で,
となり,90%以上の確率でクラス1へ割り当てられるまでになります.0.1で既にほぼ100%です.
このように,徐々に低下していく温度パラメータを設定し,温度が高いうちは撹乱を許す(ロジットが低いクラスにもチャンスがある)が,温度が冷めるにつれて決定論的な動作に近づく(わずかでもロジットが低ければそのクラスを切り捨てる)ようにスケジュールする方法を,焼きなまし法(アニーリング:annealing)といいます(逆に言えば,温度を上げていくと一様分布へ近づいていくことになります).
Gumbel-Softmax Relaxation
softmax関数および温度付きsoftmax関数に難点があるとすれば,それは「関数」という名を戴くことからも分かるように「同じ入力に対しては必ず同じ出力を返す」点にあります.
そもそもVQ-VAEに比べてSQ-VAEが優れている点として,argmax関数の動作をしないために微分可能であるという点と,確率的にコードベクトルを選んでいるとみなすことができ,確率が低くとも離れたところにあるコードベクトルにも選ばれるチャンスがあるという点がありました.
softmax関数はargmax関数の滑らかな(微分可能な)近似ですので,微分可能ではあっても確率的ではありません.
一方で,確率的にコードベクトルを選ぶ,すなわち複数のコードベクトルの中からいずれか1つを,それぞれの確率に基づいて確率的に選ぶという試行は,カテゴリカル分布に従いますが,カテゴリカル分布含め,確率分布を用いてのサンプリングという操作は確率的であっても微分不可能です.
微分可能な,かつ確率的な挙動をする,カテゴリカル分布の近似として,Jang et al.(2016)によりGumbel-Softmax Relaxationが導入されました.
Gumbel-Softmax Relaxationは,入力ロジットにガンベル乱数
挙動を可視化してみます.
plot Gumbel-Softmax Relaxation
def gumbel_softmax_relaxation(logits, temperature, eps=1e-10):
U = np.random.uniform(size=logits.shape)
g = -np.log(-np.log(U + eps) + eps)
y = logits + g
return softmax(y / temperature)
gumbel_probabilities = np.array([
gumbel_softmax_relaxation(sample_logit, temperature)
for temperature in temperature_step
])
fig, ax = plt.subplots()
ax.fill_between(
x=temperature_step, y1=gumbel_probabilities[:, 1], y2=1,
alpha=0.5, label='probability of class 0'
)
ax.fill_between(
x=temperature_step, y1=0, y2=gumbel_probabilities[:, 1],
alpha=0.5, label='probability of class 1'
)
ax.invert_xaxis()
ax.set_xlabel('temperature')
ax.set_ylabel('probability')
ax.legend(loc='center right')
ax.set_title(f'softmax(({sample_logit} + g) / temperature)')
ax.grid()
plt.show()

温度付きsoftmaxに比べて,値が激しく上下していることがわかります.また,実行のたびに乱数を生成するので,上図は上記コードを実行するたびに結果が変わります.まさに,確率的な挙動です.
その代償として,決定論的な挙動を失っています.緩やかにclass1が圧倒していくようには見えますが,通常の温度付きsoftmax関数と比較すると,温度が0に近づいても全くもって決定論的な動作になっていません.
これは,ガンベル乱数
というように,元のロジットから大小関係が反転してしまうのです.
そこで,ロジットとガンベル乱数の混合比を調整することのできるパタメータ,param_qを導入します.
param_q(自己アニーリング)
ここまで見てきた温度というパラメータは,step数に応じてスケジュールされたアニーリングが自動的に進行する値であり,古くは温度つきsoftmaxという形で深層学習分野へ既に導入されていました.
それに加えて,SQ-VAEでは損失に応じてモデルが動的に学習する,つまりセルフアニーリングする温度チックなパラメータとして,
SQ-VAEでは
ロジットを
実験として,温度を
plot Gumbel-Softmax Relaxation with param_q
temp = 1
param_q_list = np.linspace(1e-5, 1, 1000)
gumbel_probabilities = np.array([
gumbel_softmax_relaxation(sample_logit / (2*param_q), temp)
for param_q in param_q_list
])
fig, ax = plt.subplots()
ax.fill_between(
x=param_q_list, y1=gumbel_probabilities[:, 1], y2=1,alpha=0.5,
label='probability of class 0'
)
ax.fill_between(
x=param_q_list, y1=0, y2=gumbel_probabilities[:, 1], alpha=0.5,
label='probability of class 1'
)
ax.invert_xaxis()
ax.set_xlabel('param_q')
ax.set_ylabel('probability')
ax.legend(loc='center right')
ax.set_title(f'temperature={temp}')
ax.set_title(f'softmax(({sample_logit}/param_q + g) / {temp})')
ax.grid()
plt.show()
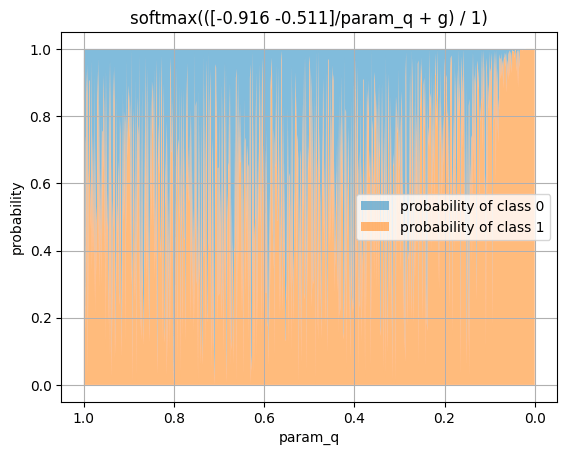
少しわかりづらいですが,逆数のグラフがベースなので,終盤に尻上がり的に,クラス1が圧倒するようになっています.
本来は対数をとった形でパラメータになっているので,横軸の対数をとってグラフを描き直してみます.
plot Gumbel-Softmax Relaxation with log_param_q
fig, ax = plt.subplots()
ax.fill_between(
x=np.log(param_q_list), y1=gumbel_probabilities[:, 1], y2=1, alpha=0.5,
label='probability of class 0'
)
ax.fill_between(
x=np.log(param_q_list), y1=0, y2=gumbel_probabilities[:, 1], alpha=0.5,
label='probability of class 1'
)
ax.invert_xaxis()
ax.set_xlabel('log(param_q)')
ax.set_ylabel('probability')
ax.legend(loc='center right')
ax.set_title(f'softmax(({sample_logit}/param_q + g) / {temp})')
ax.grid()
plt.show()

ガンベル乱数の影響を跳ねのけて,決定論的になっていく様がわかります,
という式の形からもわかるように,
SQ-VAEの実装
論文のSupplementary Materialとリポジトリのコードを参考に,SQ-VAEのモデルを構築します.論文と同じように,エンコーダとデコーダはシンプルなConvResNetとします.
リポジトリのコードとは異なり,量子化器を単体でも動くようにする目的で,また,可読性を上げる目的で,アトリビュートやメソッド周りを変更しています.また,Adam --> RAdam,ReLU --> PReLU という変更を施しています(好みの問題で,特に理由はありません).さらに,元のコードでは学習率スケジューラーのReduceLROnPlateauを使って,3エポック経っても損失が改善しない場合に学習率を半分にするという動作をさせていますが,長いエポックで回さない限りは不要と判断し,こちらは実装していません.
CT画像やMRIなどといった3次元画像にも対応可能な汎用性を持たせるため,軸操作についても変更を施しています.今回はMNISTで実験する都合上,2dで実装していますが,nn.Conv2dやnn.BatchNorm2dといったクラス名中に含まれる2dという文字を3dに書き換えるだけで,モデル全体として3次元画像に対応したものに変更できます.
まずはモデルの本体部分からです.GaussianVectorQuantizerの実装において,trainかvalidかをflg_trainによって管理し,trainの時のみ確率的な挙動(Gumbel-Softmax Relaxation)をして,validの時はargmax関数により決定論的な動作をするようにしています.
ConvBlock, ConvTransBlock, ResBlock
class ConvBlock(nn.Module):
def __init__(self, in_ch, out_ch):
super().__init__()
self.block = nn.Sequential(
nn.Conv2d(in_ch, out_ch, kernel_size=4, stride=2, padding=1, bias=False),
nn.BatchNorm2d(out_ch),
nn.PReLU()
)
def forward(self, x):
return self.block(x)
class ConvTransBlock(nn.Module):
def __init__(self, in_ch, out_ch):
super().__init__()
self.block = nn.Sequential(
nn.BatchNorm2d(in_ch),
nn.PReLU(),
nn.ConvTranspose2d(in_ch, out_ch, kernel_size=4, stride=2, padding=1, bias=True),
)
def forward(self, x):
return self.block(x)
class ResBlock(nn.Module):
def __init__(self, ch):
super().__init__()
self.block = nn.Sequential(
nn.PReLU(), # 論文ではReLU
nn.Conv2d(ch, ch, kernel_size=3, stride=1, padding=1, bias=False),
nn.BatchNorm2d(ch),
nn.PReLU(),
nn.Conv2d(ch, ch, kernel_size=1, stride=1, bias=False),
nn.BatchNorm2d(ch)
)
def forward(self, x):
return self.block(x) + x
Encoder, Decoder, GaussianVectorQuantizer
class Encoder(nn.Module):
def __init__(self,
input_ch,
encoder_mid_ch,
book_dim,
conv_block_num,
res_block_num
):
super().__init__()
output_ch_list = list(np.around(
np.geomspace(encoder_mid_ch, book_dim, num=conv_block_num)
).astype(int))
input_ch_list = [input_ch] + output_ch_list[:-1]
self.block = nn.Sequential(
*[ConvBlock(i, o) for i, o in zip(input_ch_list, output_ch_list)],
nn.Conv2d(output_ch_list[-1], book_dim,
kernel_size=4 if conv_block_num < 2 else 3,
stride=2 if conv_block_num < 2 else 1,
padding=1, bias=True),
*[ResBlock(book_dim) for _ in range(res_block_num)]
)
def forward(self, x):
return self.block(x)
class Decoder(nn.Module):
def __init__(self,
output_ch,
decoder_mid_ch_1,
decoder_mid_ch_2,
book_dim,
conv_block_num,
res_block_num
):
super().__init__()
input_ch_list = list(reversed(np.around(
np.geomspace(decoder_mid_ch_2, decoder_mid_ch_1, num=conv_block_num)
).astype(int)))
output_ch_list = input_ch_list[1:] + [output_ch]
self.block = nn.Sequential(
*[ResBlock(book_dim) for _ in range(res_block_num)],
nn.ConvTranspose2d(book_dim,
book_dim // 2 if conv_block_num < 3 else book_dim,
kernel_size=4 if conv_block_num < 2 else 3,
stride=2 if conv_block_num < 2 else 1,
padding=1, bias=False),
*[ConvTransBlock(i, o) for i, o in zip(input_ch_list, output_ch_list)],
nn.Sigmoid()
)
def forward(self, z):
return self.block(z)
class GaussianVectorQuantizer(nn.Module):
def __init__(self, book_size, book_dim, temperature_tmp=0.5, log_param_q=np.log(10.0)):
super().__init__()
self.book_size = book_size
self.book_dim = book_dim
self.book = nn.Parameter(torch.randn(book_size, book_dim))
self.set_temperature(temperature_tmp)
self.log_param_q = nn.Parameter(torch.tensor(log_param_q))
def set_temperature(self, temperature):
self.temperature = temperature
def calc_distance(self, z, book):
z = z.view(-1, self.book_dim)
distances = (torch.sum(z ** 2, dim=1, keepdim=True)
+ torch.sum(book ** 2, dim=1)
- 2*torch.matmul(z, book.t()))
return distances
def gumbel_softmax_relaxation(self, logits, temperature, eps=1e-10):
U = torch.rand(logits.shape, device=logits.device)
g = -torch.log(-torch.log(U + eps) + eps)
y = logits + g
return F.softmax(y / temperature, dim=-1)
def forward(self, z, flg_train):
original_shape, original_dims = torch.tensor(z.shape), z.dim()
permute_dims = [0, *range(2, original_dims), 1]
param_q = (1 + self.log_param_q.exp())
precision_q = 0.5 / torch.clamp(param_q, min=1e-10)
z = z.permute(permute_dims).contiguous()
logits = -self.calc_distance(z, self.book) * precision_q
probabilities = torch.softmax(logits, dim=-1)
log_probabilities = torch.log_softmax(logits, dim=-1)
if flg_train:
encodings = self.gumbel_softmax_relaxation(logits, self.temperature)
quantized_z = torch.mm(
encodings, self.book
).view(list(original_shape[permute_dims]))
avg_probs = torch.mean(probabilities.detach(), dim=0)
else:
indices = torch.argmax(logits, dim=1).unsqueeze(1)
encodings = torch.zeros(indices.shape[0], self.book_size, device=indices.device)
encodings.scatter_(1, indices, 1)
quantized_z = torch.mm(
encodings, self.book
).view(list(original_shape[permute_dims]))
avg_probs = torch.mean(encodings, dim=0)
quantized_z = quantized_z.permute(0, -1, *range(1, original_dims - 1)).contiguous()
return quantized_z, precision_q, probabilities, log_probabilities, avg_probs
GaussianSQVAE
class GaussianSQVAE(nn.Module):
def __init__(self,
image_shape,
conv_block_num,
encoder_mid_ch,
decoder_mid_ch_1,
decoder_mid_ch_2,
book_dim,
book_size,
res_block_num,
log_param_q
):
super().__init__()
input_ch = image_shape[0]
self.input_volume = math.prod(image_shape)
self.encoder = Encoder(
input_ch=input_ch, encoder_mid_ch=encoder_mid_ch, book_dim=book_dim,
res_block_num=res_block_num, conv_block_num=conv_block_num
)
self.quantizer = GaussianVectorQuantizer(
book_size=book_size, book_dim=book_dim, log_param_q=log_param_q
)
self.decoder = Decoder(
output_ch=input_ch,
decoder_mid_ch_1=decoder_mid_ch_1, decoder_mid_ch_2=decoder_mid_ch_2,
book_dim=book_dim, res_block_num=res_block_num, conv_block_num=conv_block_num
)
def calc_reconstruction_loss(self, reconstructed_x, x):
mse = F.mse_loss(reconstructed_x, x, reduction="sum") / x.shape[0]
reconstruction_loss = self.input_volume * torch.log(mse) / 2 # https://arxiv.org/abs/2102.08663
return reconstruction_loss, mse
def calc_latent_loss_and_perplexity(self,
encoded_z,
quantized_z,
precision_q,
probabilities,
log_probabilities,
avg_probs
):
kldiv_discrete = torch.sum(
probabilities * log_probabilities, dim=(0,1)
) / encoded_z.shape[0]
kldiv_continuous = torch.sum(
((encoded_z-quantized_z)**2) * precision_q, dim=list(range(1, encoded_z.dim()))
).mean()
perplexity = torch.exp(-torch.sum(avg_probs * torch.log(avg_probs + 1e-7)))
return kldiv_discrete, kldiv_continuous, perplexity
def forward(self, x, flg_train):
# Encoding
encoded_z = self.encoder(x)
# Quantization
(quantized_z, precision_q,
probabilities, log_probabilities, avg_probs) = self.quantizer(encoded_z, flg_train)
# Decoding
reconstructed_x = self.decoder(quantized_z)
# Loss
kldiv_discrete, kldiv_continuous, perplexity = self.calc_latent_loss_and_perplexity(
encoded_z, quantized_z, precision_q, probabilities, log_probabilities, avg_probs
)
reconstruction_loss, mse = self.calc_reconstruction_loss(reconstructed_x, x)
loss = dict(total=kldiv_discrete + kldiv_continuous + reconstruction_loss,
kldiv_discrete=kldiv_discrete,
kldiv_continuous=kldiv_continuous,
reconstruction=reconstruction_loss,
mse=mse,
perplexity=perplexity)
return reconstructed_x, quantized_z, loss
続いて,上のモデルを学習させるためのモジュールをLightningModuleを使って書いていきます.
GaussianSQVAEModule
class GaussianSQVAEModule(pl.LightningModule):
def __init__(self,
image_shape,
conv_block_num,
encoder_mid_ch,
decoder_mid_ch_1,
decoder_mid_ch_2,
book_dim,
book_size,
res_block_num,
log_param_q,
lr,
dataset,
transform,
train_size,
valid_size,
batch_size,
temperature_init=1.0,
temperature_decay=0.00001,
temperature_min=0.0,
):
super().__init__()
self.model = torch.nn.DataParallel(GaussianSQVAE(
image_shape=image_shape,
conv_block_num=conv_block_num,
encoder_mid_ch=encoder_mid_ch,
decoder_mid_ch_1=decoder_mid_ch_1,
decoder_mid_ch_2=decoder_mid_ch_2,
book_dim=book_dim,
book_size=book_size,
res_block_num=res_block_num,
log_param_q=log_param_q
))
self.lr = lr
self._dataset = dataset
self.transform = transform
self.train_size = train_size
self.valid_size = valid_size
self.batch_size = batch_size
self.temperature_init = temperature_init
self.temperature_decay = temperature_decay
self.temperature_min = temperature_min
def forward(self, x, flg_train):
return self.model(x, flg_train)
def configure_optimizers(self):
return torch.optim.RAdam(self.parameters(), lr=self.lr)
def setup(self, stage=None):
self.dataset = monai.data.Dataset(
[{'image': image, 'target': target} for image, target in self._dataset],
transform=self.transform
)
self.train_dataset = Subset(
self.dataset, list(range(0, self.train_size))
)
self.valid_dataset = Subset(
self.dataset, list(range(self.train_size, self.train_size + self.valid_size))
)
def train_dataloader(self):
return monai.data.DataLoader(
self.train_dataset, batch_size=self.batch_size, shuffle=True, drop_last=True,
num_workers=2, pin_memory=True
)
def val_dataloader(self):
return monai.data.DataLoader(
self.valid_dataset, batch_size=self.batch_size, shuffle=False, drop_last=True,
num_workers=2, pin_memory=True
)
def prepare_batch(self, batch):
x, y = batch['image'], batch['target']
return x, y
def _set_temperature(self):
temperature = np.max([
self.temperature_init * np.exp(-self.temperature_decay*self.global_step),
self.temperature_min
])
return temperature
def training_step(self, batch, batch_idx):
x, y = self.prepare_batch(batch)
temperature_current = self._set_temperature()
self.model.module.quantizer.set_temperature(temperature_current)
reconstructed_x, quantized_z, loss = self(x, flg_train=True)
self.log_dict(
{'train_total': loss["total"],
'train_kldiv_discrete': loss["kldiv_discrete"],
'train_kldiv_continuous': loss["kldiv_continuous"],
'train_reconstruction': loss["reconstruction"],
'train_mse': loss["mse"],
'train_perplexity': loss["perplexity"],
'log_param_q': self.model.module.quantizer.log_param_q},
batch_size=self.batch_size, on_step=False, on_epoch=True, logger=True
)
if batch_idx == 0:
torch.save(
reconstructed_x.detach().cpu(),
str(Path(self.logger.log_dir).joinpath(
f'train_epoch{self.current_epoch:03}_reconstructed.pt'
))
)
torch.save(
quantized_z.detach().cpu(),
str(Path(self.logger.log_dir).joinpath(
f'train_epoch{self.current_epoch:03}_quantized_{y}.pt'
))
)
return loss["total"]
def validation_step(self, batch, batch_idx):
x, y = self.prepare_batch(batch)
reconstructed_x, quantized_z, loss = self(x, flg_train=False)
self.log_dict(
{'valid_total': loss["total"],
'valid_kldiv_discrete': loss["kldiv_discrete"],
'valid_kldiv_continuous': loss["kldiv_continuous"],
'valid_reconstruction': loss["reconstruction"],
'valid_mse': loss["mse"],
'valid_perplexity': loss["perplexity"],},
batch_size=self.batch_size, on_epoch=True
)
if batch_idx == 0:
torch.save(
reconstructed_x.detach().cpu(),
str(Path(self.logger.log_dir).joinpath(
f'valid_epoch{self.current_epoch:03}_reconstructed.pt'
))
)
torch.save(
quantized_z.detach().cpu(),
str(Path(self.logger.log_dir).joinpath(
f'valid_epoch{self.current_epoch:03}_quantized_{y}.pt'
))
)
eval_params
def eval_params(name,
book_dim=64,
lr=0.001,
transform=None,
train_size=10000,
valid_size=200,
batch_size=32,
temperature_init=1.0,
temperature_decay=1e-5,
temperature_min=0.0,
):
return dict(
image_shape={'mnist': (1, 28, 28), 'cifar': (3, 32, 32), 'hq': (3, 256, 256)}[name],
conv_block_num={'mnist': 1, 'cifar': 2, 'hq': 3}[name],
encoder_mid_ch={'mnist': 32, 'cifar': 32, 'hq': 16}[name],
decoder_mid_ch_1={'mnist': 32, 'cifar': 32, 'hq': 64}[name],
decoder_mid_ch_2={'mnist': 32, 'cifar': 32, 'hq': 16}[name],
book_dim=book_dim,
book_size={'mnist': 128, 'cifar': 512, 'hq': 512}[name],
res_block_num={'mnist': 2, 'cifar': 6, 'hq': 6}[name],
lr=lr,
dataset={'mnist': mnist_dataset, 'cifar': cifar_dataset, 'hq': None}[name],
transform=transform,
train_size=train_size,
valid_size=valid_size,
batch_size=batch_size,
log_param_q={'mnist': np.log(10), 'cifar': np.log(20), 'hq': np.log(20)}[name],
temperature_init=temperature_init,
temperature_decay=temperature_decay,
temperature_min=temperature_min,
)
MNISTデータセットを使って20エポック回してみます.MNISTを含めtorchvisionのデータセットは,値が[0, 1]の範囲にclampされているため,特に前処理は必要ないものとします.また,データサイズも十二分にあるため,augumentationも行いません.
fit
pl.seed_everything(0, workers=True)
max_epoch = 20
name = ['mnist', 'cifar', 'hq'][0]
evaled_params = eval_params(
name=name,
# transform=monai.transforms.Compose(
# [monai.transforms.NormalizeIntensityd(keys=['image'], nonzero=False, channel_wise=False)]
# ),
transform=None
)
g_sqvae_plmodule = GaussianSQVAEModule(**evaled_params)
logger = CSVLogger(save_dir='output', name=name)
print(f'{logger.log_dir=}')
trainer = pl.Trainer(
max_epochs=max_epoch,
deterministic='warn',
logger=logger,
log_every_n_steps=10,
)
trainer.fit(model=g_sqvae_plmodule)
学習中のメトリクスの変遷を可視化すると,以下のようになります.
plot metrics
name ='mnist'
version = 0
df = pd.read_csv(f'output/{name}/version_{version}/metrics.csv')
x_value = 'epoch'
column_list = ['total', 'latent', 'reconstruction', 'mse', 'perplexity']
fig, axes = plt.subplots(1, 6, figsize=(6.4 * 6, 4.8))
for i, column in enumerate(column_list):
for j, prefix in enumerate(['train', 'valid']):
column_name = prefix + '_' + column
tmp_df = df[[x_value, column_name]].dropna()
axes[i].plot(
tmp_df[x_value], tmp_df[column_name], c=plt.get_cmap("tab10")(j), label=prefix
)
axes[i].set_title(column)
axes[i].legend()
param_q = 'log_param_q'
tmp_df = df[[x_value, param_q]].dropna()
axes[-1].plot(tmp_df[x_value], tmp_df[param_q], c=plt.get_cmap("tab10")(0), label=param_q)
axes[-1].set_title(param_q)
plt.show()

前に述べた通り,学習により自己アニーリングが進んで,log_param_qの値が小さくなっていることがわかります.
損失は total = kldiv_discrete + kldiv_continuous + reconstruction_loss という計算になっています.
reconstruction_lossは「再構成がうまくいかないこと」への損失です.reconstruction_lossは,mse(画素値同士の平均二乗誤差)のlogをとったものに,画像の画素数を掛け合わせて算出されています.
kldiv_continuousは「エンコーダの出力と量子化器の出力が似ていないこと」への損失です.この値がtrainよりもvalidのほうが大きいのは,以下の理由によると思われます.まず,潜在空間上において,似た性質を持つコードベクトル同士が群を成し,群ごとに,ある点を中心とした同一超球面上に並ぶように学習されます.そして,エンコーダは,この超球の中心にめがけて埋め込みをする,いわば中庸的な埋め込みを学習します.

validでは,argmaxによるone-hot行列(最近傍のコードベクトルに対応する列だけ1で他が0な疎行列)を作成し,それを用いた行列積をすることによって最近傍に割り当てられます.そのため,エンコーダによって埋め込まれた位置から最近傍のコードベクトルまでの距離が,そのまま損失となります.一方でtrainでは,softmaxによる確率行列(それぞれのコードベクトルに割り当てられる確率を要素とする密行列)を用いた行列積を計算することによって,各コードベクトルの線形和へ「埋め込み」(割り当てではない)されます.同一超球面上のコードベクトルの確率ベクトルによる線形和は,超球の中心に近い中庸的なものになります.量子化器の出力がエンコーダの出力の方に勝手に近づいてくるため,損失は小さくなります.

まとめると,trainにおいては,エンコーダは「中庸的なところに落とすと勝手に損失が小さくなることを発見したぜ!」というずる賢い学習をし,しかしその戦略はvalidでは通用しないため,trainとvalidで損失の乖離が発生することになります.
ちなみに,このtrainにおけるずる賢い学習を抑制する方法として,温度を低くすることがあげられます.先に見たように,温度が下がることによって,softmaxの結果が確率行列からone-hot行列へ近づく(argmaxの結果の結果へ近づく)ためです.
perplexityは使われるコードベクトルが多様であるほど高くなるメトリクスであり,大きい値が望ましいものになります.量子化後のコードベクトルの使用率を使って計算し,どのコードベクトルも等しい割合(確率)で使われたとき,最大となります.コードベクトルが2つだった場合(2値分類)として実験すると以下のようになります:
plot example of perplexity
def calc_perplexity(avg_probs):
return torch.exp(-torch.sum(avg_probs * torch.log(avg_probs + 1e-5)))
avg_probs_0 = torch.linspace(1e-5, 1 - 1e-5, 100)
avg_probs_1 = 1 - avg_probs_0
avg_probs = torch.stack([avg_probs_0, avg_probs_1], dim=0).T
perplexities = [calc_perplexity(avg_prob) for avg_prob in avg_probs]
plt.plot(avg_probs_0, perplexities)
plt.xlabel('probability of class0 (= 1 - (probability of class1))')
plt.ylabel('perplexity')
plt.title('Perplexity in 2-classes Classification')
plt.show()

kldiv_discreteは一般にエントロピー(平均情報量)と呼ばれるものに、マイナスを掛けたものを損失としたものです。量子化前のロジットを用いて計算します。perplexityの対数をとってマイナスを掛けたような(あくまで「ような」です)値になっています.したがって,perplexityと対照的な動きをします.
plot example of kldiv_discrete
def calc_kldiv_discrete(logits):
probabilities = torch.softmax(logits, dim=-1)
log_probabilities = torch.log_softmax(logits, dim=-1)
return torch.sum(probabilities * log_probabilities)
logits = torch.log(avg_probs) # general solution with arbitrary constant C
kldiv_discretes = [calc_kldiv_discrete(logit) for logit in logits]
plt.plot(softmax(logits, axis=1)[:, 0], kldiv_discretes)
plt.xlabel('probability of class0 (= 1 - (probability of class1))')
plt.ylabel('kldiv_discrete')
plt.title('kldiv_discrete in 2-classes Classification')
plt.show()
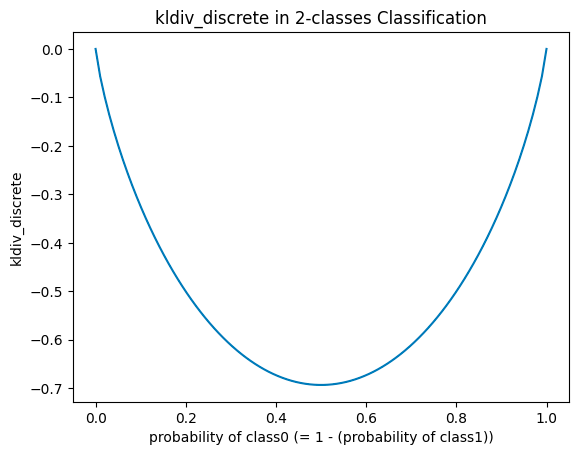
つまり,どのコードベクトルにも等しい確率が割り当てられるときに損失は最小となります.VQ-VAEに比べてSQ-VAEはコードベクトルの使用に多様さが生まれると述べましたが,このkldiv_discreteが多様性を増やす方向に働く損失となります.ただし,デコーダへの入力がいつまでも確率的な挙動をしているとreconstruction_lossが小さくならないため,kldiv_discreteとreconstruction_lossの間にはトレードオフの関係があると思われます.
学習中のメトリクスのグラフからは,絶対値が圧倒的に大きいreconstruction_lossを最小化するようにモデルが学習していることが読み取れます.実際,mseはtrain,validともにゼロに漸近しており,再構成がかなりうまくいっていることが予想されます.
各エポックの1バッチ目の再構成画像を可視化してみます.1行が1エポックに対応し,下に行くほどエポックが進みます.バッチ内の先頭10画像だけを20エポックぶん可視化します.まずはtrainからです.
plot train_reconstructed_x
num = 10
train_reconstructed_x_path_list = sorted(
Path(f'output/{name}/version_{version}').glob('train_epoch*[0-9]_reconstructed.pt')
)
length = len(train_reconstructed_x_path_list)
fig, axes = plt.subplots(length, num, figsize=(num * 2, length * 2))
for i, path in enumerate(train_reconstructed_x_path_list):
train_reconstruced_x = torch.load(path)
for j, image in enumerate(train_reconstruced_x[:num]):
axes[i, j].imshow(image.permute(1,2,0))
plt.show()
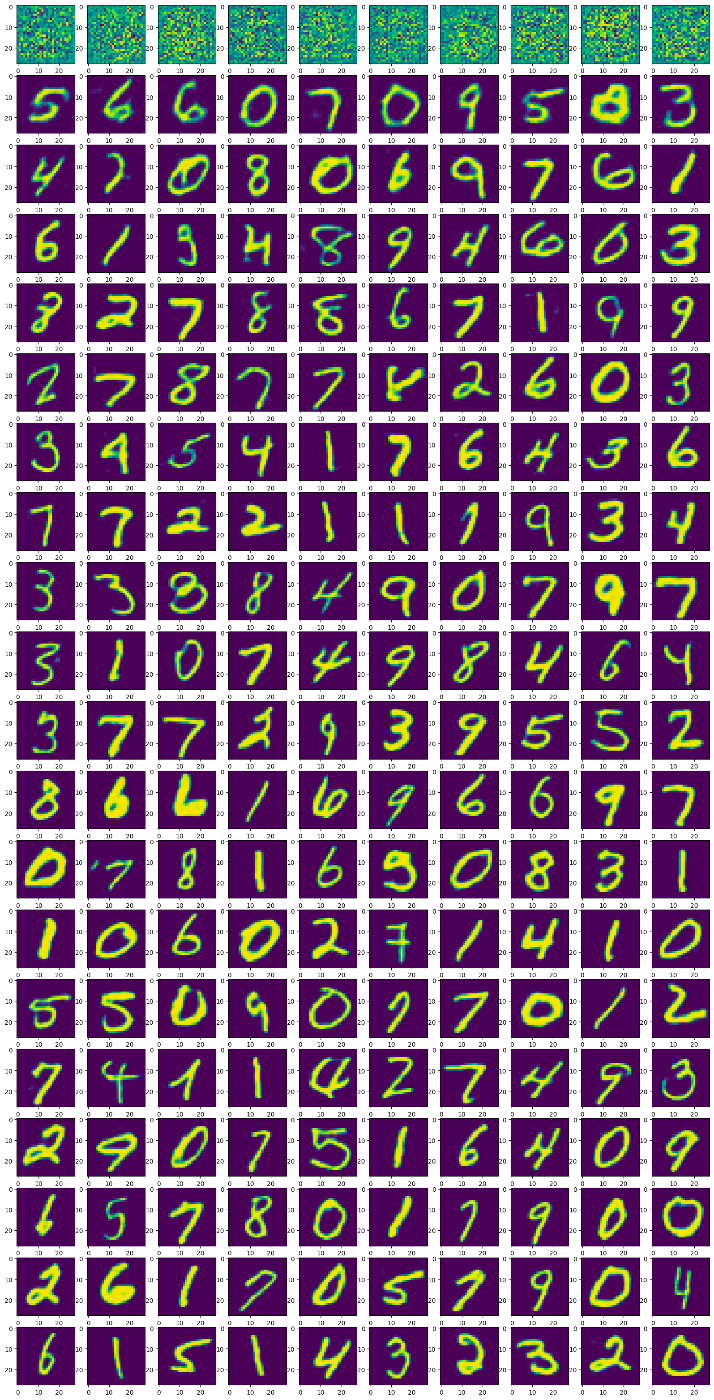
当然1エポック目はモザイクしか再構成できていませんが,2エポック目で既に十分に再構成できるようになっています.
続いてvalidの再構成画像を見てみます.最後の行は入力画像です.
plot valid_reconstructed_x
valid_reconstructed_x_path_list = sorted(
Path(f'output/{name}/version_{version}').glob('valid_epoch*[0-9]_reconstructed.pt')
)
fig, axes = plt.subplots(length + 1, num, figsize=(num * 2, length * 2))
for i, path in enumerate(valid_reconstructed_x_path_list):
valid_reconstruced_x = torch.load(path)
for j, image in enumerate(valid_reconstruced_x[:num]):
axes[i, j].imshow(image.detach().cpu().permute(1,2,0))
valid_dataset = Subset(
evaled_params['dataset'],
list(range(eval_params(name)['train_size'], eval_params(name)['train_size'] + num))
)
for j, (image, _) in enumerate(valid_dataset):
axes[-1, j].imshow(image.permute(1,2,0))
plt.show()

1エポック目だけはもやもやしたノイズが入ってしまっていますが,それ以外は再構成がうまくいっており,20エポックも必要なかった(3エポック程度で十分だった)ことがわかります.
最後に,潜在空間上のノイズから新しい画像を生成してみます.エンコーダの出力と同じ形状の,ガウス分布からの乱数をデーコーダにひとつまみ…
random_noise = torch.randn([1, 64, 7, 7])
generated = g_sqvae_plmodule.model.module.decoder(random_noise)
plt.imshow(generated[0].detach().cpu().permute(1,2,0))
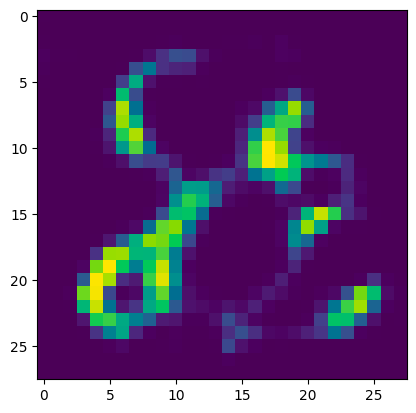
…8っぽい何かと2っぽい何かがくっついた画像が生成されました.
結語
SQ-VAEはハイパーパラメータが実質的にlog_param_qの初期値だけという手軽さにもかかわらず,安定して学習が進行し,再構成もうまくいくことが確認できました.
ただし,潜在空間の次元についてはリポジトリのデフォルト値をそのまま使用しています.
デフォルトのコードでは,潜在空間では画像の縦横はそれぞれ4分の1(したがって面積は16分の1)になるものの,その分チャンネル方向は64次元へ拡大されるので,冒頭に述べた圧縮器としてエンコーダが機能しているかというと,いまひとつに思われます.
また,潜在空間のノイズから新しい画像を生成するのにもまだまだ改善の余地がありそうです.最終的には,より画素数の多い画像や3D画像での実験も行っていく予定です.
Discussion