シェーダーめも その 1
とりあえずレイマーチング理解するまでが「その 1」
GLSL リファレンス
レイマーチング
- 解決したい課題
- 画面上の特定のピクセルから飛ぶレイが物体と交差しているか?
- ピクセル
- 画像上の特定の一点の色情報 vec4 RGBA
- レイ
- 始点と向きを持つ線
- 長さ 1 に正規化 (単位ベクトル)
レイが物体と交差している→物体を描く
レイが物体と交差していない→背景を描く
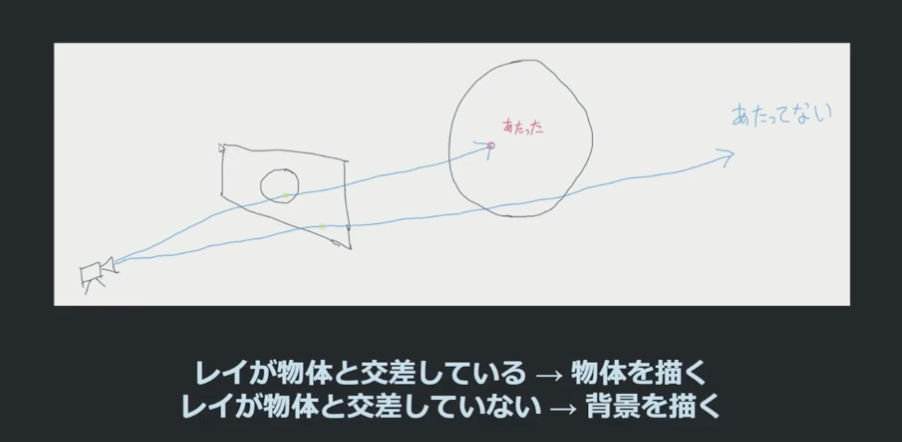
カメラからピクセルに対応するレイが飛び、物体との交差判定が行われる様子(これとても分かりやすい)

uv 座標とは
- uv 座標
- 2D空間における位置を表すための座標系の一種で、通常、各次元の座標が 0から1の範囲に正規化された値で指定される。たとえば、(0.0, 0.0) が画像やテクスチャの左下、(1.0, 1.0) が右上を意味するように使われる。
- シェーダーでは、しばしば画面座標(
fragCoord)をレンダリング解像度(iResolution)で割ることで uv 座標に変換し、テクスチャの参照やエフェクトの適用に利用する。

screenPos

レイを作る(始点、方向)

- レイの始点 rayOrigin =カメラ位置という理解でまずはあっているのよね?レイを飛ばす始点。
- カメラ位置が固定であるなら、ここは固定値にする。
- カメラ位置は動かせるから、レイの始点自体は必ずしも固定ではない。むしろ動かして映像のカメラワークを作る。
- レイの向き rayDirection は単位ベクトル

レイマーチングと距離関数
レイマーチングは、距離関数を用いてレイの始点 rayOri からレイの向き rayDir の方向にレイを探索しながら進めていき(レイを進める、行進させる、マーチングさせる・する→レイマーチング ray marching)、物体と交差しているかを判定するアルゴリズム。
距離関数は、レイマーチングにて始点からレイを進めるときの 1 ステップ=1 探索(for 文 1 回分と考えると良い)で進む距離を算出する関数である。

- 距離関数
- 空間位置を渡すと、一番近い表面までの距離を返す関数。この関数自体には方向の情報は無いので注意。あくまで現在の空間位置から一番近い表面までの距離というスカラー値を返すだけ。
- 値
- 物体の表面:0(下図ピンクの線)
- 物体の表面から離れる(物体の外側):正
- 物体の表面から離れる(物体の内側):負
この可視化すごく理解捗る

レイマーチングのアルゴリズム概要

レイマーチング
- 解決したい課題
- 画面上の特定のピクセルから飛ぶレイが物体と交差しているか?
- ピクセル
- 画像上の特定の一点の色情報 vec4 RGBA
- レイ
- 始点と向きを持つ線
- 長さは持たない
レイが物体と交差している→物体を描く
レイが物体と交差していない→背景を描く

カメラからピクセルに対応するレイが飛び、舞台との交差判定が行われる様子(これとても分かりやすい)

初めてのレイマーチング on GLSL Sandbox
#extension GL_OES_standard_derivatives : enable
precision highp float;
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
float distanceFunction(vec3 pos, float radius) {
float d = length(pos) - radius;
return d;
}
void main( void ) {
// gl_FragCoord: スクリーン座標 (x, y) = (0 ~ x 軸方向の px, 0 ~ y 軸方向の px)
// uv: UV 座標 (x, y) = (0 ~ 1, 0 ~ 1)、スクリーン座標を 0 ~ 1 に正規化した座標系
// vec2 uv = gl_FragCoord.xy / resolution.xy;
// スクリーン空間を変更する (x, y) = (-1 ~ 1, -1 ~ 1)
// 1. 座標を2 倍して平行移動
vec2 coordDouble = gl_FragCoord.xy * 2.0; // スクリーン座標を 2 倍. (x, y) = (0 ~ 2 xMax, 0 ~ 2 yMax)
vec2 p = coordDouble - resolution.xy; // スクリーン座標を平行移動 (x, y) = (- xMax ~ + xMax, - yMax ~ + yMax)
// 2. スケールを保ったまま小さい方の解像度で正規化
// p.x /= resolution.x;
// p.y /= resolution.y;
// p.x /= max(resolution.x, resolution.y);
// p.y /= max(resolution.x, resolution.y);
p.x /= min(resolution.x, resolution.y);
p.y /= min(resolution.x, resolution.y);
// vec2 p = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
// カメラを定義
// 1. カメラ位置の定義
float cameraY = -10. + sin(time) * 5.;
// float cameraZ = -10. + sin(3. * time) * 5.;
float cameraZ = -2.5;
vec3 cameraPos = vec3(0., 0., cameraZ);
// 2. スクリーン平面とカメラの距離の定義
// スクリーン平面をどれだけカメラ位置から遠ざけるか。
// このパラメータを大きくすると、カメラとスクリーン平面が離されカメラの視野角 FOV が狭くなり、小さくするとカメラがスクリーン平面に近づいて視野角が広くなる。
// float screenZ = 3. + sin(3. * time) * 5.;
float screenZ = 2.5;
// レイの方向を定義
// カメラ位置から各ピクセルに向けたレイ rayDirection を定義
vec3 rayDirection = normalize(vec3(p, screenZ));
// 球を定義
// float radius = sin(3. * time);
float radius = 0.5;
// レイを行進する(レイマーチングする
vec3 rayPosition;
float depth = 0.0;
float dist; // 少なくとも 1 回は代入される
float distThreshold = 0.001;
vec3 col = vec3(1.0);
for (int i = 0; i < 99; i++) {
rayPosition = cameraPos + rayDirection * depth;
float dist = distanceFunction(rayPosition, radius);
depth += dist;
if (dist < distThreshold) {
col = vec3(0.0, 0.0, 0.0);
// col = vec3(0.0, cos(3. * time), 0.0);
break;
}
}
// float len = length(rayPosition);
col *= exp(-0.1 * dist);
gl_FragColor = vec4(col, 1.0);
}

スクリーン座標をアスペクト比を保ったまま正規化する
各軸のピクセル数で正規化する
各軸の長さの単位が異なる形になる。
例えば、横 1000 px(x 軸)、縦 500 px(y 軸)の場合、
各軸を書く軸のピクセル数で正規化した場合、
- x 軸は 0.001 で 1 px を表す(1 / 1000 [unit/px])
- y 軸は 0.002 で 1 px を表す(1 / 500 [unit/px])
すると、(0.5, 0.5) は (500 px, 250 px) を表す。
この状態で例えば半径 0.5 の円を書こうとすると、
レイマーチングにて小さい方の解像度でスクリーン座標を正規化する理由 by o3-mini
たとえば、解像度が横 800px、縦 600px の場合を考えてみましょう。
個別に解像度で割る場合
- x 軸: (x / 800)
- y 軸: (y / 600)
この方法だと、同じ「1」という数値が実際には横と縦で違う物理的な大きさになります。たとえば、シーン中に「半径 0.5 の円」を描こうとしても、x 軸方向では 400px 分、y 軸方向では 300px 分の大きさになるため、実際の描画結果は横に引き延ばされた楕円になってしまいます。
min(resolution.x, resolution.y) で割る場合
- 解像度の小さい方(この例では 600px)で両方を割るので、
- x 軸: (x / 600)
- y 軸: (y / 600)
このようにすると、x 軸も y 軸も同じ基準で正規化されるので、シーン内の単位が均一になり、もともと円として定義した形は実際にも円として描かれます。
なぜレイマーチングでは大切か
レイマーチングでは、各ピクセルからの光線(レイ)の進行距離やオブジェクトとの距離を正確に計算する必要があります。もしスケールが軸によって異なると、オブジェクトの形状や距離の計算にズレが生じ、シーン全体が歪んでしまう可能性があります。均一なスケールにするために、最小の解像度で割る手法がよく使われます。
このように、min(resolution.x, resolution.y) を使うことで、どちらの軸も同じ「長さ単位」で扱えるようになり、シーンが歪むのを防ぐことができるのです。
大きい方で割ってしまうと、シーン内の基準スケールがずれてしまいます。
たとえば、解像度が横 800px、縦 600px の場合、
-
大きい方で割る(800)場合:
- x 軸: (x / 800)
- y 軸: (y / 800)
この場合、y 軸は実際のピクセル数に対して「過剰に縮小」され、実際に描画すると、正しく円として描かれるべき図形が縦に伸びたり縮んだりして、形が変わってしまいます。
なぜなら、x 軸と y 軸の正規化に使う基準が統一されず、y 軸は本来の大きさより小さく扱われるため、アスペクト比が崩れてしまうからです。
一方、最小値で割る(600)場合、
- x 軸: (x / 600)
- y 軸: (y / 600)
とすることで、どちらの軸も同じ単位でスケールされ、シーン全体の形が歪むことなく描画されるようになります。
つまり、大きい方で割ると縦または横のどちらかが「余計に縮まって」しまい、シーンが歪む原因になるため、均一なスケーリングを行うためには、最小値を用いるのが適切なのです。
カメラ
視錐台
視錐台理解
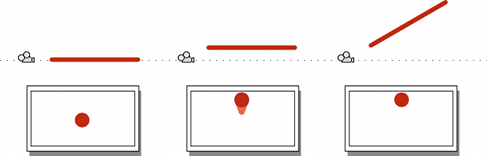
イメージの外端はイメージの隅に相当する境界線により定義されます。もし直線をカメラに向かって後ろ向きに辿った場合、最終的にひとつの点につながります。Unity では、この点はカメラの transform 位置と一致し、パースペクティブの中心と呼びます。画面の上端の中心と、パースペクティブの中心と、下端の中心とを、結んでできる角度は field of view (略して FOV) と呼ばれます。
前述のように、境界線の外にあるものはカメラにより表示されませんが、その他にも何をレンダリングするかについて二つの制約があります。ニアクリッピングプレーンとファークリッピングプレーンはカメラの XY 平面と平行で、中心から直線上である距離でセットされます。ニアクリッピングプレーンよりカメラに近いもの、ファークリッピングプレーンより遠いものは、レンダリングされません。
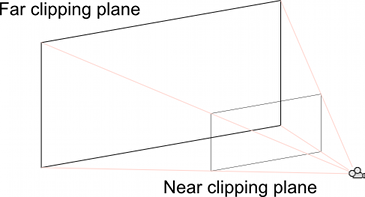
二つのクリッピングプレーンと境界線により切り取られたピラメッドの形状ができて、これを視錐台と呼びます。
prompt: スクリーン座標をアスペクト比を保ったまま正規化する方法について整理して。以下について詳細に説明して。例を用いる場合、x, y を (1000 px, 500 px) にしてください。正規化は [0, 1] にマッピングするようにしてください。
- 各軸を各軸のピクセル数で正規化する方法
- 各軸をピクセル数の最大値で正規化する方法
- 各軸をピクセル数の最小値で正規化する方法
Answer
以下、解像度 (1000 px, 500 px) の例を用いて、スクリーン座標をアスペクト比を保ったまま正規化する方法を説明します。ここでは、スクリーン座標
1. 各軸をそれぞれのピクセル数で正規化する方法
各軸ごとに独立して正規化する方法では、x 軸は横のピクセル数、y 軸は縦のピクセル数で割ります。
-
式:
x' = \frac{x}{1000}, \quad y' = \frac{y}{500} -
例:
例えば、あるピクセル座標(x,y)=(500,250)
x' = \frac{500}{1000} = 0.5, \quad y' = \frac{250}{500} = 0.5. -
特徴:
この方法はそれぞれの軸が独自のスケールで正規化されるため、実際の[0, 1]
2. 各軸をピクセル数の最大値で正規化する方法
各軸を解像度のうち大きい方(この例では x 軸のピクセル数 1000 px)で正規化すると、どちらの軸も同じ基準で割ることになります。
-
式:
x' = \frac{x}{1000}, \quad y' = \frac{y}{1000} -
例:
同じく(500, 250)
x' = \frac{500}{1000} = 0.5, \quad y' = \frac{250}{1000} = 0.25. -
特徴:
この方法では、y 軸が実際の解像度(500 px)よりも大きな値(1000)で割られるため、y 軸方向のスケールが縮まります。結果として、アスペクト比が変化してしまい、正規化後の座標系上では縦方向が相対的に圧縮された状態となります。
3. 各軸をピクセル数の最小値で正規化する方法
各軸を解像度のうち小さい方(この例では y 軸のピクセル数 500 px)で正規化する方法です。
-
式:
x' = \frac{x}{500}, \quad y' = \frac{y}{500} -
例:
(500, 250)
x' = \frac{500}{500} = 1.0, \quad y' = \frac{250}{500} = 0.5. -
特徴:
この方法では、どちらの軸も同じ 500 px を基準に正規化されるため、物理的なスケールが統一されます。結果として、座標系内での比率は変わらず、また、アスペクト比も「内部的な計算」で一貫性を保ちやすくなります。ただし、[0,1]
まとめ
-
各軸独立の正規化
x' = \frac{x}{1000},\ y' = \frac{y}{500}
→ アスペクト比そのまま、各軸が解像度に応じたスケール。 -
最大値で正規化
x' = \frac{x}{1000},\ y' = \frac{y}{1000}
→ y 軸が圧縮され、アスペクト比が変化する。 -
最小値で正規化
x' = \frac{x}{500},\ y' = \frac{y}{500}
→ 両軸のスケールを統一でき、内部計算(例:カメラ空間での計算)では一貫性を持たせやすい。
このように、どの方法を採用するかはその後の処理(例:レイマーチングやカメラ空間への変換)でどのように座標を利用するかに依存します。アスペクト比を保ちながら内部的な計算を行う場合は、最小値で正規化する方法がよく用いられます。
それぞれの方法での正規化後の値
1. 各軸を各軸のピクセル数で正規化する方法
各軸ごとに正規化すると、
座標の範囲は、
- 正規化前
- 正規化後
2. 各軸をピクセル数の最大値で正規化する方法
最大値(この例では 1000 px)で正規化すると、
-
x' 0.1
-
y' 0.1
※この方法では、実際の
座標の範囲は、
- 正規化前
- 正規化後
3. 各軸をピクセル数の最小値で正規化する方法
最小値(この例では 500 px)で正規化すると、
-
x' 0.1
-
y' 0.1
※この場合、どちらの軸も同じ基準で割るため、内部的には両軸が同じスケールとなります(ただし
座標の範囲は、
- 正規化前
- 正規化後
まとめ
このように、どの方法を使うかで同じ正規化値
1. 各軸を各軸のピクセル数で正規化する方法
2. 各軸をピクセル数の最大値で正規化する方法
3. 各軸をピクセル数の最小値で正規化する方法
グリッド
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 resolution; // 画面の解像度(ピクセル単位)
uniform float time;
// edge 以下なら 0. edge より上なら 1.
float stepForGrid(float edge, float target) {
if (target <= edge) {
return 0.;
} else {
return 1.;
}
}
void main(void) {
// グリッドの設定
float gridSpacing = 200.; // グリッド1セルのサイズ(px)
float lineWidth = 50.0; // 線の太さ(px)
// 現在のピクセル座標
// - 正規化なし
vec2 pos = gl_FragCoord.xy;
// - 各軸のピクセル数で正規化
// vec2 pos = gl_FragCoord.xy / resolution.xy;
// 各軸のピクセル座標をグリッド間隔で割ったあまりを求め、あまりが線幅内(ここでは 1 px)であれば線を描画する
// 1. x, y 軸それぞれで、最も近いグリッド線からの距離を計算
// ref: mod - https://registry.khronos.org/OpenGL-Refpages/es3.1/html/mod.xhtml
// ref: floor - https://registry.khronos.org/OpenGL-Refpages/es3.1/html/floor.xhtml
// x - y * floor(x / y). ex) 550px - 100px * floor (550 / 100) = 550 px - 500 px = 50 px;
float distancePxFromXGrid = mod(pos.x, gridSpacing);
float distancePxFromYGrid = mod(pos.y, gridSpacing);
// 2. どちらかが線幅以内なら線として描画する
// step(edge, target) = 0.0 if target < edge, 1.0 if edge <= target
// ref: step - https://registry.khronos.org/OpenGL-Refpages/es3.1/html/step.xhtml
// edge = modX が 0(x = 0 px, 100 px, 200px, ...)のとき、target = lineWidth = 1.0 で、edge 以上 (edge <= target)、つまり step(0., 1.0) = 1.0
// edge = modX が 1(x = 1 px, 101 px, 201px, ...)のとき、target = lineWidth = 1.0 で、edge 以上 (edge <= target)、つまり step(1., 1.0) = 1.0
// edge = modX が 2(x = 2 px, 102 px, 202px, ...)のとき、target = lineWidth = 1.0 で、edge 未満 (target < edge)、つまり step(2., 1.0) = 0.0
// ...
// edge = modX が 99(x = 99 px, 199 px, 299px, ...)のとき、target = lineWidth = 1.0 で、edge 以上 (edge <= target)、つまり step(99., 1.0) = 0.0
// edge = modX が 100 は存在しない
// float edge = distancePxFromXGrid; // 1.0, 2.0, 3.0, ..., 99.0
// float target = lineWidth; // 1.0 固定
//float xIsOnGrid = step(edge, target); // x 座標がグリッド上にいるか
float xIsOnGrid = stepForGrid(distancePxFromXGrid, lineWidth);
float yIsOnGrid = stepForGrid(distancePxFromYGrid, lineWidth);
//float yIsOnGrid = step(distancePxFromXGrid, lineWidth); // y 座標がグリッド上にいるか
// x か y どちらかがグリッド上にいるか。1.0 以上ならどちらかがグリッド上にいる。
// 0 <= coordIsOnGrid <= 2.0
float coordIsOnGrid = xIsOnGrid + yIsOnGrid;
// float coordIsOnGrid = xIsOnGrid;
// ref: clamp - https://registry.khronos.org/OpenGL-Refpages/es3.1/html/clamp.xhtml
// clamp 関数で RGB 値が 0 ~ 1 になるように変換
coordIsOnGrid = clamp(coordIsOnGrid, 0.0, 1.0); // clamp(target, minVal, maxVal)
// 背景を白、グリッド線を黒にする
// ref: mix - https://registry.khronos.org/OpenGL-Refpages/es3.1/html/mix.xhtml
/*
en:
`mix` performs a linear interpolation between x and y using a to weight between them. The return value is computed as follows: x⋅(1−a)+y⋅a
For the variants of mix where a is genBType, elements for which a[i] is false, the result for that element is taken from x,
and where a[i] is true, it will be taken from y. Components of x and y that are not selected are allowed to be invalid floating point values and will have no effect on the results.
ja:
mix は、x と y の間で線形補間を行い、a を重みとして使用します。返される値は次の式で計算されます:
x⋅(1−a)+y⋅a
mix の a が genBType(ブール型の配列)であるバリエーションの場合、a[i] が false の要素については x の対応する要素が結果として使用され、a[i] が true の要素については y の要素が使用されます。
x と y のうち選択されなかった成分は、無効な浮動小数点値であっても許容され、計算結果には影響を与えません。
*/
vec3 rgbWhite = vec3(1.); // rgb(1., 1., 1.)
vec3 rgbRed = vec3(1., 0., 0.);
vec3 rgbBlue = vec3(0., 0., 1.);
vec3 rgbBlack = vec3(0.); // rgb(0., 0., 0.)
float linearInterpolationWeight = coordIsOnGrid;
vec3 color = mix(rgbWhite, rgbRed, linearInterpolationWeight);
/*
if (distancePxFromXGrid > 0.00) {
color = mix(rgbWhite, rgbBlack, linearInterpolationWeight); // coordIsOnGrid は 0.0 か 1.0 なので、グリッド上なら黒、グリッド上でないなら白が選択される
} else {
color = mix(rgbWhite, rgbBlue, linearInterpolationWeight); // coordIsOnGrid は 0.0 か 1.0 なので、グリッド上なら黒、グリッド上でないなら白が選択される
}
*/
// color = vec3(0., 0., distancePxFromXGrid / gridSpacing);
/*
float r, g, b;
g = ((distancePxFromXGrid / gridSpacing) + (distancePxFromYGrid / gridSpacing)) / 2.;
b = (distancePxFromXGrid / gridSpacing) / 2.;
// b = ((distancePxFromXGrid / gridSpacing) + (distancePxFromYGrid / gridSpacing)) / 2.;
// color = vec3(0., 0., b);
float ratio = ((5. * sin(2. * time) + 7.) / 1.); // [-1, 1] -> [-5, 5] -> [0, 10] -> [0, 5]
color = vec3(0., 0., b * ratio);
*/
if (mod(pos.x, gridSpacing) - 0.5 <= 0.001) {
color = rgbBlack;
} else {
color = rgbWhite;
}
gl_FragColor = vec4(color, 1.0);
}
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 resolution; // 画面の解像度(ピクセル単位)
uniform float time;
void main(void) {
// グリッドの設定
float gridSpacing = 100.; // グリッド1セルのサイズ(px)
float lineWidth = 1.; // 線の太さ(px)
// 定数ベクター
vec3 rgbWhite = vec3(1.); // rgb(1., 1., 1.)
vec3 rgbRed = vec3(1., 0., 0.);
vec3 rgbBlue = vec3(0., 0., 1.);
vec3 rgbBlack = vec3(0.); // rgb(0., 0., 0.)
// グリッドの計算
float distancePxFromGridX = mod(gl_FragCoord.x - 0.5, gridSpacing);
float distancePxFromGridY = mod(gl_FragCoord.y - 0.5, gridSpacing);
// 現在のピクセル座標がグリッド上か(このピクセルを塗るか)判定
bool isOnGridX = distancePxFromGridX < lineWidth; // 0 px, 1 px, ..., 50 px, 51 px, ...
bool isOnGridY = distancePxFromGridY < lineWidth;
bool isOnGrid = isOnGridX && isOnGridY;
vec3 color;
if (isOnGrid) {
color = rgbBlack;
} else {
color = rgbWhite;
}
gl_FragColor = vec4(color, 1.0);
}
ピクセル操作:しましま色のグリッドをびよんびよんする
グリッドでピクセル操作を学んだ
#extension GL_OES_standard_derivatives : enable
precision highp float;
uniform float time;
uniform vec2 resolution;
void main( void ) {
vec2 pos = gl_FragCoord.xy - 0.5;
// グリッドの設定
float gridSpacing = 50.; // グリッド 1 セルのサイズ(px)
float gridSpacingDiff = sin(time) * gridSpacing / 3. - gridSpacing / 3.;
gridSpacing += gridSpacingDiff;
float lineWidth = 5.; // グリッドの幅(px)
// グリッドの描画をするかどうかの計算
float distancePxFromGridX = mod(pos.x, gridSpacing);
float distancePxFromGridY = mod(pos.y, gridSpacing);
bool isOnGridX = distancePxFromGridX < lineWidth;
bool isOnGridY = distancePxFromGridY < lineWidth;
bool isOnGrid = isOnGridX || isOnGridY;
// グリッドの色の計算:x 軸、y 軸にしましまカラーを作る
float numX100 = floor((pos.x - mod(pos.x, gridSpacing)) / gridSpacing); // 100 の位の数
float numY100 = floor((pos.y - mod(pos.y, gridSpacing)) / gridSpacing); // 100 の位の数
bool isXEven = mod(numX100, 2.) <= 0.0001; // 100 の位が偶数かどうか
bool isYEven = mod(numY100, 2.) <= 0.0001; // 100 の位が偶数かどうか
bool isBlue = (!isXEven && !isYEven) || (isXEven && isYEven);
// カラーベクター
vec3 rgbWhite = vec3(1.);
float wave = sin(time) / 2. + 0.5; // [0, 1.0]
float invWave = 1. - wave;
vec3 rgbRed = vec3(invWave, 0., 0.);
vec3 rgbBlue = vec3(0., 0., wave);
vec3 color;
if (isOnGrid) {
if (isBlue) {
color = rgbBlue;
} else {
color = rgbRed;
}
} else {
color = rgbWhite;
}
gl_FragColor = vec4(color, 1.0);
}
GPU 処理のイメージ湧いてきた
Shuffle box を読む
基本と同時にかっこいいシェーダーを見ながら勉強した方が良い気がしてきた

ソースコード全体
はい、なにもわからん
#if HW_PERFORMANCE==1
const float MAX_DISPERSE = 10.;
const float MAX_BOUNCE = 5.;
#else
const float MAX_DISPERSE = 5.;
const float MAX_BOUNCE = 5.;
#endif
//#define ALTERNATIVE
//#define ALTERNATIVE2
// HG_SDF
// https://www.shadertoy.com/view/Xs3GRB
#define PI 3.14159265359
#define saturate(x) clamp(x, 0., 1.)
void pR(inout vec2 p, float a) {
p = cos(a)*p + sin(a)*vec2(p.y, -p.x);
}
float smax(float a, float b, float r) {
vec2 u = max(vec2(r + a,r + b), vec2(0));
return min(-r, max (a, b)) + length(u);
}
float vmax(vec2 v) {
return max(v.x, v.y);
}
float vmin(vec2 v) {
return min(v.x, v.y);
}
float vmax(vec3 v) {
return max(max(v.x, v.y), v.z);
}
float vmin(vec3 v) {
return min(min(v.x, v.y), v.z);
}
float fBox(vec2 p, vec2 b) {
vec2 d = abs(p) - b;
return length(max(d, vec2(0))) + vmax(min(d, vec2(0)));
}
float fBox(vec3 p, vec3 b) {
vec3 d = abs(p) - b;
return length(max(d, vec3(0))) + vmax(min(d, vec3(0)));
}
float sdLine( vec3 p, float h, float r )
{
p.y -= clamp( p.y, 0.0, h );
return length( p ) - r;
}
// Spectrum palette
// IQ https://www.shadertoy.com/view/ll2GD3
vec3 pal( in float t, in vec3 a, in vec3 b, in vec3 c, in vec3 d ) {
return a + b*cos( 6.28318*(c*t+d) );
}
vec3 spectrum(float n) {
return pal( n, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(1.0,1.0,1.0),vec3(0.0,0.33,0.67) );
}
//========================================================
// Modelling
//========================================================
float time;
float invertg;
float sin3(vec3 v) {
return sin(v.x) * sin(v.y) * sin(v.z);
}
vec2 map(vec3 p) {
float scl = 1.3;
p /= scl;
pR(p.yz, .2 * PI);
pR(p.xz, -.25 * PI);
float flr = p.y+.5;
#ifdef ALTERNATIVE
p += sin(p * 08. + (time * vec3(-1,-1,-1) + vec3(0,.5,.75)) * PI * 2.) * .1;
#else
p += sin(p * 08. + time * vec3(1,3,2) * PI * 2. + vec3(0,.5,3)) * .1;
#endif
// p += sin(p * 07. + (time * vec3(-1,1,1) + vec3(0)) * PI * 2.) * .1;
vec3 p2 = p;
p += sin3(p * 80.) * .0015;
float b = length(p) - .66;
b = fBox(p, vec3(.5 - .01)) - .01;
float d3 = 1e12;
float rr = .0025;
p2 = abs(p2);
p2 = vec3(vmin(p2.xz), p2.y, vmax(p2.xz));
d3 = min(d3, sdLine(p2.xzy - vec3(.5,.7,.5), .2, rr));
d3 = max(d3, -vmax(p*vec3(1,-1,-1)));
#ifdef ALTERNATIVE
float e = .1;
p.x += sin(p.x * 04. + (time * -1. + .0) * PI * 2.) * e;
p.z += sin(p.z * 04. + (time * -1. + sign(p.x) * .25 + .25) * PI * 2.) * e;
p.y += sin(p.y * 04. + (time * -1. + sign(p.z) * .25) * PI * 2.) * e;
#else
p += sin(p * 06. + time * vec3(-3,2,1) * PI * 2. * 1. + vec3(.1,.5,.6)) * .1;
#endif
b = smax(b, -vmin(abs(p)) + .0125, .01);
float d2 = b + .1;
float d = max(b, -d2 + .01);
d *= invertg;
d2 = max(d2+.001, b);
float id = 1.;
if (d2 < d)
{
id = 3.;
d = d2;
}
#ifndef ALTERNATIVE2
if (d3 < d) {
d = d3;
id = 4.;
}
#endif
d *= scl;
return vec2(d, id);
}
//========================================================
// Lighting
//========================================================
vec3 BGCOL = vec3(.86,.8,1);
float intersectPlane(vec3 rOrigin, vec3 rayDir, vec3 origin, vec3 normal, vec3 up, out vec2 uv) {
float d = dot(normal, (origin - rOrigin)) / dot(rayDir, normal);
vec3 point = rOrigin + d * rayDir;
vec3 tangent = cross(normal, up);
vec3 bitangent = cross(normal, tangent);
point -= origin;
uv = vec2(dot(tangent, point), dot(bitangent, point));
return max(sign(d), 0.);
}
mat3 envOrientation;
vec3 light(vec3 origin, vec3 rayDir) {
origin = -origin;
rayDir = -rayDir;
origin *= envOrientation;
rayDir *= envOrientation;
vec2 uv;
vec3 pos = vec3(-6);
float hit = intersectPlane(origin, rayDir, pos, normalize(pos), normalize(vec3(-1,1,0)), uv);
float l = smoothstep(.75, .0, fBox(uv, vec2(.5,2)) - 1.);
l *= smoothstep(6., 0., length(uv));
return vec3(l) * hit;
}
vec3 env(vec3 origin, vec3 rayDir) {
origin = -(vec4(origin, 1)).xyz;
rayDir = -(vec4(rayDir, 0)).xyz;
origin *= envOrientation;
rayDir *= envOrientation;
float l = smoothstep(.0, 1.7, dot(rayDir, vec3(.5,-.3,1))) * .4;
return vec3(l) * BGCOL;
}
//========================================================
// Marching
//========================================================
#define ZERO (min(iFrame,0))
// https://iquilezles.org/articles/normalsSDF
vec3 normal( in vec3 pos )
{
vec3 n = vec3(0.0);
for( int i=ZERO; i<4; i++ )
{
vec3 e = 0.5773*(2.0*vec3((((i+3)>>1)&1),((i>>1)&1),(i&1))-1.0);
n += e*map(pos+0.001*e).x;
}
return normalize(n);
}
struct Hit {
vec2 res;
vec3 p;
float len;
float steps;
};
Hit march(vec3 origin, vec3 rayDir, float invert, float maxDist, float understep) {
vec3 p;
float len = 0.;
float dist = 0.;
vec2 res = vec2(0.);
vec2 candidate = vec2(0.);
float steps = 0.;
invertg = invert;
for (float i = 0.; i < 800.; i++) {
len += dist * understep;
p = origin + len * rayDir;
candidate = map(p);
dist = candidate.x;
steps += 1.;
res = candidate;
if (dist < .00005) {
break;
}
if (len >= maxDist) {
len = maxDist;
res.y = 0.;
break;
}
}
return Hit(res, p, len, steps);
}
mat3 sphericalMatrix(vec2 tp) {
float theta = tp.x;
float phi = tp.y;
float cx = cos(theta);
float cy = cos(phi);
float sx = sin(theta);
float sy = sin(phi);
return mat3(
cy, -sy * -sx, -sy * cx,
0, cx, sx,
sy, cy * -sx, cy * cx
);
}
mat3 calcLookAtMatrix(vec3 ro, vec3 ta, vec3 up) {
vec3 ww = normalize(ta - ro);
vec3 uu = normalize(cross(ww,up));
vec3 vv = normalize(cross(uu,ww));
return mat3(uu, vv, ww);
}
// Hex tiling, FabriceNeyret2
// https://www.shadertoy.com/view/4dKXR3
float hex(vec2 U) {
U *= mat2(1,-1./1.73, 0,2./1.73) *5.; // conversion to
vec3 g = vec3(U,1.-U.x-U.y), g2, // hexagonal coordinates
id = floor(g); // cell id
g = fract(g); // diamond coords
if (length(g)>1.) g = 1.-g; // barycentric coords
g2 = abs(2.*fract(g)-1.); // distance to borders
// length(g2) = distance to center
return length(1.-g2);
}
// http://filmicworlds.com/blog/filmic-tonemapping-operators/
vec3 tonemap2(vec3 texColor) {
texColor /= 2.;
texColor *= 16.; // Hardcoded Exposure Adjustment
vec3 x = max(vec3(0),texColor-0.004);
return (x*(6.2*x+.5))/(x*(6.2*x+1.7)+0.06);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
#ifdef ALTERNATIVE
float duration = 4.;
#else
float duration = 8.;
#endif
time = mod(iTime / duration + .1, 1.);
//time= 0.;
envOrientation = sphericalMatrix(((vec2(81.5, 119) / vec2(187)) * 2. - 1.) * 2.);
vec2 uv = (2. * fragCoord - iResolution.xy) / iResolution.y;
#ifdef ALTERNATIVE2
uv /= 3.;
#endif
#ifdef ALTERNATIVE
float h = hex(uv.yx * 1.08 + time * vec2(.1,.172) * -2.);
#else
float h = hex(uv.yx * 1.08 + time * vec2(.1,.172) * 2.);
#endif
h -= .03;
h /= length(fwidth(uv * 10.));
h = 1. - saturate(h);
Hit hit, firstHit;
vec2 res;
vec3 p, rayDir, origin, sam, ref, raf, nor, camOrigin, camDir;
float invert, ior, offset, extinctionDist, maxDist, firstLen, bounceCount, wavelength;
vec3 col = vec3(0);
vec3 bgCol = BGCOL * .08 * .5;
vec3 bgCol2 = bgCol * .3;
bgCol = mix(bgCol, bgCol2, h);
invert = 1.;
maxDist = 15.;
float fl = 20.;
camOrigin = vec3(0,0,9.5 * fl);
camDir = normalize(vec3(uv * .168, -fl));
firstHit = march(camOrigin, camDir, invert, maxDist * fl, .6);
firstLen = firstHit.len;
float steps = 0.;
for (float disperse = 0.; disperse < MAX_DISPERSE; disperse++) {
invert = 1.;
sam = vec3(0);
origin = camOrigin;
rayDir = camDir;
extinctionDist = 0.;
wavelength = disperse / MAX_DISPERSE;
float rand = texture(iChannel0, (fragCoord + floor(iTime * 60.) * 10.) / iChannelResolution[0].xy).r;
wavelength += (rand * 2. - 1.) * (.5 / MAX_DISPERSE);
bounceCount = 0.;
vec3 nor;
for (float bounce = 0.; bounce < MAX_BOUNCE; bounce++) {
if (bounce == 0.) {
hit = firstHit;
} else {
hit = march(origin, rayDir, invert, 1.2, .6);
}
steps += hit.steps;
res = hit.res;
p = hit.p;
if (invert < 0.) {
extinctionDist += hit.len;
}
// hit background
if ( res.y == 0.) {
break;
}
if ( res.y == 4.) {
break;
}
nor = normal(p);
ref = reflect(rayDir, nor);
if (res.y > 1.) {
break;
}
// shade
sam += light(p, ref) * .5;
sam += pow(max(1. - abs(dot(rayDir, nor)), 0.), 5.) * .1;
sam *= vec3(.85,.85,.98);
// refract
float ior = mix(1.2, 1.8, wavelength);
ior = invert < 0. ? ior : 1. / ior;
raf = refract(rayDir, nor, ior);
bool tif = raf == vec3(0); // total internal reflection
rayDir = tif ? ref : raf;
offset = .01 / abs(dot(rayDir, nor));
origin = p + offset * rayDir;
//invert = tif ? invert : invert * -1.;
invert *= -1.; // not correct but gives more interesting results
bounceCount = bounce;
}
if (res.y > 1.) {
sam = vec3(0);
sam += light(p, ref) * .5;
sam += pow(max(1. - abs(dot(rayDir, nor)), 0.), 5.) * .1;
sam *= vec3(.85,.85,.98);
vec3 cc = res.y == 2. ? vec3(1) : vec3(.033);
rayDir = refract(rayDir, nor, 1./1.3);
sam += env(p, rayDir) * cc;
}
if (bounceCount == 0.) {
// didn't bounce, so don't bother calculating dispersion
col += sam * MAX_DISPERSE;
break;
}
if (res.y < 2.) {
sam += env(p, rayDir);
}
vec3 extinction = vec3(.5,.5,.5) * .0;
extinction = 1. / (1. + (extinction * extinctionDist));
col += sam * extinction * spectrum(-wavelength+.25);
}
col /= MAX_DISPERSE;
if (bounceCount == 0. && res.y == 0.) {
col = bgCol;
}
if (res.y == 4.) {
col = bgCol2;
}
col = pow(col, vec3(1.19)) * 2.5;
col = tonemap2(col);
fragColor = vec4(col, 1.);
}