【第四回】非線形微分方程式系のベイズ推定 with Stan: 階層ベイズモデル
はじめに
第三回で複数時系列データを扱えるように拡張しました。今回は、階層ベイズモデルに拡張することで、群ごとのパラメータのばらつきを扱えるようにしたいと思います。まず今まで使ってきたアリの採餌動員モデルを再掲しておきます。
階層モデルについて
階層モデルでは、各グループのパラメータを「全体平均」と「グループ差」に分解して表現します。この時「グループ差」は正規分布に従うと仮定します。今回は、1つの時系列データを「グループ」として考えます。もしコロニー差みたいなものを考えたい場合は、由来コロニーが同じ時系列を1つの「グループ」と扱えばよいです。
アリの採餌動員モデルにおけるパラメータ
と記述できます。さらに、「グループ差」
これらを簡潔に一つの式でまとめると
となります。このパイパーパラメータ
Stanによる実装
事前分布は以下のものを与えます。
functions { // モデル式の宣言
vector beekman(real t, vector x, array[] real par) {
vector[1] dxdt;
real a = par[1]/10000;
real b = par[2]/100000;
real s = par[3];
real n_total = par[4];
dxdt[1] = (a + b * x[1]) * (n_total - x[1]) - (s * x[1]) / (s + x[1]);
return dxdt;
}
}
data {
int<lower=0> Series; // 時系列のデータ数
int<lower=0> N; // 1時系列のデータ数
array[Series, N] real<lower=0> ts; // 時間
array[Series, N] real<lower=0> x; // ts=tにおける個体数
array[Series, N] real<lower=0> n_total; // 総個体数
}
parameters {
array[Series] real<lower=0> a;
array[Series] real<lower=0> b;
array[Series] real<lower=0> s;
real<lower=0> mu_a;
real<lower=0> mu_b;
real<lower=0> mu_s;
real<lower=0> sigma_a;
real<lower=0> sigma_b;
real<lower=0> sigma_s;
array[Series] real<lower=0> sigma;
array[Series] vector<lower=0>[1] x0;
}
transformed parameters {
array[Series, 4] real par;
for (i in 1:Series) {
par[i, 1] = a[i];
par[i, 2] = b[i];
par[i, 3] = s[i];
par[i, 4] = n_total[i, 1];
}
}
model {
// priors
mu_a ~ normal(0, 100);
mu_b ~ normal(0, 100);
mu_s ~ normal(0, 100);
sigma_a ~ cauchy(0, 2.5);
sigma_b ~ cauchy(0, 2.5);
sigma_s ~ cauchy(0, 2.5);
for (i in 1:Series) {
a[i] ~ normal(mu_a, sigma_a);
b[i] ~ normal(mu_b, sigma_b);
s[i] ~ normal(mu_s, sigma_s);
sigma[i] ~ cauchy(0, 2.5);
x0[i, 1] ~ uniform(0, n_total[i, 1]);
}
// 各時系列ごとにODEを解く
for (i in 1:Series) {
array[N] vector[1] mu = ode_rk45(beekman, x0[i,], 0, ts[i, 1:N], par[i,]);
for (j in 1:N) {
x[i,j] ~ normal(mu[j], sigma[i]);
}
}
}
generated quantities {
array[Series, N] vector[1] mu_pred;
for (i in 1:Series){
mu_pred[i,] = ode_rk45(beekman, x0[i,], 0, ts[1, 1:N], par[i,]);
}
}
実行
以下の6個の時系列データを使用します。各パラメータの全体平均と標準偏差を推定するので前回より多いデータ数にしています。生成に使ったコードは省略しますが、基本的には以前のコードに少し改変を加えただけです。私のGitHubから見ることができます。真の値は

library(tidyverse)
library(rstan)
library(bayesplot)
library(ggplot2)
library(cmdstanr)
library(tidybayes)
raw_data <- read.csv("all_data_3.csv")
data <- raw_data %>% select(series, time, x_obs, n_total)
series_ids <- unique(data$series)
x_list <- map(series_ids, ~ data %>%
filter(series == .x) %>%
pull(x_obs))
ts_list <- map(series_ids, ~ data %>%
filter(series == .x) %>%
pull(time))
n_list <- map(series_ids, ~ data %>%
filter(series == .x) %>%
pull(n_total))
ts_lengths <- map(ts_list, length)
input <- list(
Series = length(series_ids),
N = ts_lengths[1],
ts = ts_list,
x = x_list,
n_total = n_list
)
stan <- cmdstan_model("model3.stan")
fit <- stan$sample(data = input, iter_warmup = 2000, iter_sampling = 2000, parallel_chains = 4, chains = 4, save_warmup = TRUE)
color_scheme_set("brewer-RdYlBu")
plt_dens <- mcmc_dens_overlay(fit$draws(c("mu_a", "mu_b", "mu_s"), inc_warmup = F)) + geom_density(linewidth = 1) + theme_classic()
plt_dens2 <- mcmc_dens_overlay(fit$draws(c("sigma_a", "sigma_b", "sigma_s"), inc_warmup = F)) + geom_density(linewidth = 1) + theme_classic()
color_scheme_set("blue")
plt_trace <- mcmc_trace(fit$draws(c("mu_a", "mu_b", "mu_s", "sigma_a", "sigma_b", "sigma_s"), inc_warmup = T), n_warmup = 2000) + theme_classic()
plt_pairs <- mcmc_pairs(fit$draws(c("mu_a", "mu_b", "mu_s"), inc_warmup = F), off_diag_args = list(size = 0.5, alpha = 0.5))
plt_pairs2 <- mcmc_pairs(fit$draws(c("sigma_a", "sigma_b", "sigma_s"), inc_warmup = F), off_diag_args = list(size = 0.5, alpha = 0.5))
ggsave("trace_plot3.png", plot = plt_trace, width = 1000, height = 800, units = "px", dpi = 180)
ggsave("dens_plot3-1.png", plot = plt_dens, width = 1000, height = 400, units = "px", dpi = 180)
ggsave("dens_plot3-2.png", plot = plt_dens2, width = 1000, height = 400, units = "px", dpi = 180)
ggsave("pairs_plot3-1.png", plot = plt_pairs, width = 1000, height = 800, units = "px", dpi = 180)
ggsave("pairs_plot3-2.png", plot = plt_pairs2, width = 1000, height = 800, units = "px", dpi = 180)
df_xpred <- fit$draws(format = "df") %>%
spread_draws(mu_pred[series, time, vector]) %>%
mode_hdi(.width = 0.95) # MAP推定値と95%CIの計算
df_list <- split(df_xpred, df_xpred$series) # series列で分割してリストに格納
list2env(setNames(df_list, paste0("df", 1:6)), envir = .GlobalEnv) # 各リスト要素を df1, df2, df3 に代入
plt_fitting <- ggplot(df1, aes(x = time)) +
geom_ribbon(aes(ymin = .lower, ymax = .upper), fill = "#D53E4F", alpha = 0.4) +
geom_line(aes(y = mu_pred), linewidth = 1, col = "#D53E4F") +
geom_ribbon(data = df2, aes(ymin = .lower, ymax = .upper), fill = "#cd9c32", alpha = 0.4) +
geom_line(data = df2, aes(y = mu_pred), linewidth = 1, col = "#cd9c32") +
geom_ribbon(data = df3, aes(ymin = .lower, ymax = .upper), fill = "#32CD32", alpha = 0.4) +
geom_line(data = df3, aes(y = mu_pred), linewidth = 1, col = "#32CD32") +
geom_ribbon(data = df4, aes(ymin = .lower, ymax = .upper), fill = "#41b4e2", alpha = 0.4) +
geom_line(data = df4, aes(y = mu_pred), linewidth = 1, col = "#41b4e2") +
geom_ribbon(data = df5, aes(ymin = .lower, ymax = .upper), fill = "#4169E2", alpha = 0.4) +
geom_line(data = df5, aes(y = mu_pred), linewidth = 1, col = "#4169E2") +
geom_ribbon(data = df6, aes(ymin = .lower, ymax = .upper), fill = "#a70de4", alpha = 0.4) +
geom_line(data = df6, aes(y = mu_pred), linewidth = 1, col = "#a70de4") +
geom_line(data = data, aes(x = time, y = x_obs, group = as.factor(series), col = as.factor(series))) +
geom_point(data = data, aes(x = time, y = x_obs, group = as.factor(series), col = as.factor(series))) +
labs(x = "時間", y = "観測個体数", color = "系列") +
theme_classic() +
labs(x = "時間", y = "観測個体数")
ggsave("fitting_plot3.png", plot = plt_fitting, width = 1000, height = 800, units = "px", dpi = 180)
結果
出力した結果が以下のようになります。推定結果には各系列の
> print(fit$summary(),n=40)
# A tibble: 661 × 10
variable mean median sd mad q5 q95 rhat ess_bulk
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -1983. -1983. 9.33 9.31 -1999. -1968. 1.00 649.
2 mu_a 43.0 42.8 7.18 6.30 32.1 54.6 1.00 1905.
3 mu_b 15.4 15.2 3.40 3.01 10.4 21.3 1.00 3364.
4 mu_s 9.38 9.32 1.36 1.20 7.32 11.6 1.00 2545.
5 sigma_a 3.36 2.02 4.33 1.97 0.256 11.0 1.01 516.
6 sigma_b 6.18 5.70 3.02 2.42 2.25 11.6 1.00 1949.
7 sigma_s 1.51 1.18 1.34 1.07 0.105 3.99 1.01 718.
8 a[1] 43.3 43.0 5.67 5.44 34.5 53.0 1.00 2434.
9 a[2] 42.3 42.3 8.05 6.78 29.1 54.6 1.00 2091.
10 a[3] 43.1 42.8 8.04 6.77 31.0 56.0 1.00 2195.
11 a[4] 43.2 42.9 8.96 6.73 30.6 56.5 1.00 2385.
12 a[5] 43.1 42.8 8.82 6.88 30.5 56.2 1.00 2235.
13 a[6] 43.3 42.8 9.06 6.80 30.5 56.7 1.00 2328.
14 b[1] 15.4 15.0 6.56 5.83 5.22 27.1 1.00 3846.
15 b[2] 14.7 14.6 1.53 1.47 12.4 17.4 1.00 2408.
16 b[3] 7.76 7.47 2.05 1.78 4.95 11.5 1.00 1752.
17 b[4] 15.4 15.3 1.66 1.59 12.8 18.2 1.00 3422.
18 b[5] 16.1 16.2 2.61 2.56 11.7 20.2 1.00 2103.
19 b[6] 23.2 23.7 5.18 5.06 14.1 31.0 1.00 1630.
20 s[1] 9.76 9.48 2.49 1.67 6.61 13.8 1.00 2768.
21 s[2] 9.90 9.79 1.42 1.35 7.78 12.5 1.00 2029.
22 s[3] 10.1 9.79 1.67 1.40 7.82 13.2 1.00 1642.
23 s[4] 9.44 9.40 1.16 1.10 7.61 11.4 1.00 3354.
24 s[5] 8.64 8.69 1.47 1.45 6.11 11.0 1.00 2100.
25 s[6] 8.36 8.52 1.84 1.80 5.17 11.1 1.00 1646.
26 sigma[1] 5.16 5.14 0.371 0.358 4.60 5.81 1.00 10479.
27 sigma[2] 28.3 28.2 2.08 2.04 25.1 32.0 1.00 8242.
28 sigma[3] 24.7 24.6 1.81 1.74 21.9 27.9 1.00 10993.
29 sigma[4] 24.0 23.9 1.73 1.71 21.3 27.0 1.00 10574.
30 sigma[5] 25.3 25.2 1.81 1.77 22.5 28.4 1.00 9584.
31 sigma[6] 16.6 16.6 1.21 1.18 14.8 18.7 1.00 9303.
32 x0[1,1] 4.81 4.39 3.18 3.38 0.481 10.6 1.00 6861.
33 x0[2,1] 99.2 99.1 5.22 5.17 90.7 108. 1.00 3208.
34 x0[3,1] 207. 207. 7.37 7.16 194. 219. 1.00 3668.
35 x0[4,1] 298. 298. 8.37 8.19 284. 312. 1.00 5060.
36 x0[5,1] 407. 407. 10.4 10.1 389. 424. 1.00 4851.
37 x0[6,1] 516. 516. 9.00 8.72 500. 530. 1.00 5927.
38 par[1,1] 43.3 43.0 5.67 5.44 34.5 53.0 1.00 2434.
39 par[2,1] 42.3 42.3 8.05 6.78 29.1 54.6 1.00 2091.
40 par[3,1] 43.1 42.8 8.04 6.77 31.0 56.0 1.00 2195.
# ℹ 621 more rows
# ℹ 1 more variable: ess_tail <dbl>
# ℹ Use `print(n = ...)` to see more rows






階層化しなかった場合との比較
第三回のコードでデータだけ入れ替えて推定を行ってみましょう。このモデルでは、すべての時系列で
> fit$summary()
# A tibble: 640 × 10
variable mean median sd mad q5 q95 rhat ess_bulk
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -2198. -2198. 2.93 2.86 -2203. -2194. 1.00 2564.
2 a 18.5 21.9 7.81 4.28 1.90 26.2 1.01 644.
3 b 7.34 7.11 0.948 0.856 6.13 9.17 1.01 724.
4 s 3.17 3.09 0.474 0.443 2.54 4.07 1.01 867.
.......(略).......
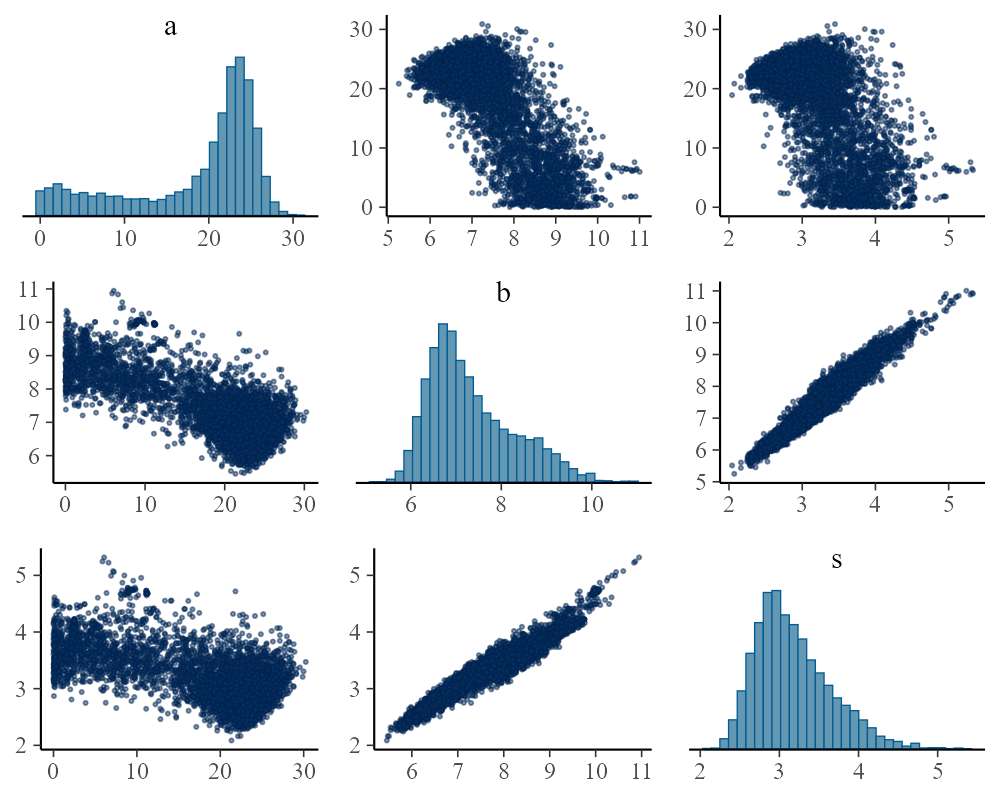

まとめ
今回は、それぞれのパラメータの異質性を考慮できる階層ベイズモデルへの拡張についてご紹介しました。階層化によって全体の傾向
Discussion