はじめに
本記事ではConstrained Policy Optimizationについて解説していこうと思います。なるべく丁寧に、数式や証明も詳細に記述していきたいと思っていますが、もしなにか間違いや不明瞭な点があればぜひ指摘していただけると幸いです。
強化学習は今日まで様々な手法が提案されており、多岐に渡る領域で強化学習が適用されています。強化学習の
代表的な手法には
- Policy Gradient Method (勾配降下法)
- Q学習
- Actor-Critic Method
などが挙げられます。今回の記事ではPolicy Gradient Methodの中の一つのConstrained Policy Optimization Methodを紹介していこうと思います。なお、前提知識としてPolicy Gradient MethodとTrust Region Policy Optimizatino(TRPO)が必須となります。本記事でも軽く触れますが、この二つに関しては他の解説記事も参考にされることをお勧めします。
強化学習について
強化学習は(S, A, p_0, p, \gamma) によってマルコフ決定過程(MDP)として定義することができます。ここで、Sはすべての状態の集合を表し、Aは行動の集合です。r(s,a) : S \times A \rightarrow \mathbb{R} は報酬関数を示し、p_0(s) は初期状態の確率分布、p(s'|s,a) : S \times A \times S \rightarrow [0,1] は環境遷移関数を表し、\gamma \in [0,1] は割引率です。強化学習の目的は、以下の割引報酬の期待和を最大化する方策\pi_{\theta}(a|s)を発見することです。なお\thetaは方策モデルのパラメータです(例としてはニューラルネットワークのパラメータなど)。
J(\theta) = \mathbb{E}{s_0, a_0, s_1, a_1, \cdots, s_T, a_T}\left[\sum_{t=0}^{T} \gamma^t r(s_t, a_t)\right]
ここで各行動は方策\pi(\cdot|s_i)からサンプルされたものとし(a_i \sim \pi_{\theta}(\cdot|s_i))、初期位置s_0は初期状態の確率分布p_0(s)からサンプリングされたものとします。
Background
1. 勾配降下法(Policy Gradient Method)
Policy Gradient Methodは強化学習の中では最もシンプルな考え方をした手法で、特に制御工学で最適制御を学んだ人にとってはかなりとっつきやすい手法になっています。Policy Gradientは以下の最適化問題を解く手法になっています。
\begin{equation}
\underset{\theta}{\operatorname{max}} \quad J(\theta)
\end{equation}
直感的な説明だと、報酬関数のJ(\theta)を最大化する\thetaを求めるということになります。これは制約なしの最適化問題なのでステップサイズを\alphaとすると以下のように\thetaを逐次更新すれば最適値が求まります。
\begin{equation}
\theta_{i+1} = \theta_i + \alpha \nabla J(\theta)
\end{equation}
今回は最大化問題なので\alphaの前の符号は+になることに注意。詳しい説明は他の記事に譲りますが\nabla J(\theta)は以下のように計算できます。こちらの導出はpolicy gradient methodの他記事を参考にしていただければ出てきます。
\begin{equation}
\nabla J(\theta) = \mathbb{E}{s_0, a_0, s_1, a_1, \cdots, s_T, a_T}\left[\sum_{t=0}^{T} \nabla_{\theta} \log{\pi_{\theta}}(a_t | s_t) \gamma^t r(s_t, a_t)\right]
\end{equation}
これも詳しい説明は他の記事に譲りますが、勾配計算の時には\gamma^t r(s_t, a_t)ではなく他の値を使うことが多く、今後の説明の簡易化のため今回はアドバンテージ関数A(s_t, a_t) = Q(s_t, a_t) - V(s_t)を使うと仮定します。そのため式(3)は以下のように書き直せます。
\nabla J(\theta) = \mathbb{E}{s_0, a_0, s_1, a_1, \cdots, s_T, a_T}\left[\sum_{t=0}^{T} \nabla_{\theta} \log{\pi_{\theta}}(a_t | s_t) A(s_t, a_t)\right]
2. Trust Region Policy Optimization (TRPO)
前の章で勾配降下法を導入しました。ただ、この手法はただの最適化問題を解いているだけなのでシンプルで分かりやすいのですが、一つ大きな問題を孕んでいます。それは式(2)の\thetaの更新時に適切なステップサイズ\alphaを使わないと計算が不安定になり、最適な解に収束しないという点です。学習が安定しないので\alphaを小さくするという方法も考えられますが、それだとなかなか学習が進みません。そこで出された解決方法がTRPOと呼ばれる手法です。TRPOでは以下の最適化問題をといて\thetaを更新していきます(この最適化問題の導出は省略)。
\begin{equation}
\begin{split}
&\underset{\theta}{\operatorname{max}} \quad \mathbb{E}_{s_i \sim p(\cdot | s_{i-1}, a_{i-1}), a_i \sim \pi_{\theta_{\theta}}(\cdot|s_i)} \left[ A_{\pi_{\theta_{old}}}(s_i,a_i) \right]\\
&\text{subject to} \quad \mathbb{E}_{s_i \sim p(\cdot | s_{i-1}, a_{i-1})} \left[ D_{KL} (\pi_{\theta_{old}}(\cdot|s_i) || \pi_{\theta}(\cdot|s_i) \right] \leq \delta
\end{split}
\end{equation}
なお、s_0はp_0からサンプリングされるとします。この最適化の意味としては、なるべく多くの報酬を得られるように\thetaを最大化しつつも、\thetaを\theta_{\text{old}}から過度に変化させないように\deltaで制限しているとなります。
まず、この最適化問題の問題点として、学習後の\pi_{\theta}からactionをサンプルして期待値の計算を行わないといけないので、importance samplingを使ってこの問題を回避していきます。
\begin{equation}
\begin{split}
&\underset{\theta}{\operatorname{max}} \quad \mathbb{E}_{s_i \sim p(\cdot | s_{i-1}, a_{i-1}), a_i \sim \pi_{\theta_{old}}(\cdot|s_i)} \left[ \frac{\pi_{\theta}(a_i|s_i)}{\pi_{\theta_{old}}(a_i|s_i)} A_{\pi_{\theta_{old}}}(s_i,a_i) \right]\\
&\text{subject to} \quad \mathbb{E}_{s_i \sim p(\cdot | s_{i-1}, a_{i-1})} \left[ D_{KL} (\pi_{\theta_{old}}(\cdot|s_i) || \pi_{\theta}(\cdot|s_i) \right] \leq \delta
\end{split}
\end{equation}
これでactionは\pi_{\theta_{\text{old}}}からサンプルすればよくなりました。ただ、まだこの最適化問題を解析的にとくのは難しいので、目的関数を線形近似してKL Divergenceで表されている制約を2次近似して問題を解いていきます。
\begin{equation}
\begin{split}
\underset{\theta}{\operatorname{max}} \quad & g^\top(\theta - \theta_{old})\\
& \frac{1}{2} (\theta - \theta_{\text{old}})^{\top} H (\theta - \theta_{\text{old}}) \leq \delta
\end{split}
\end{equation}
ここで、g = \nabla L(\theta) |_{\theta_{old}} = \frac{\nabla \pi_{\theta}(a|s)|_{\theta=\theta_{\text{old}}}}{\pi_{\theta_{\text{old}}}(a|s)} A_{\pi_{\theta_{\text{old}}}}(s,a)であり、2つめの制約はKL Divergenceの2次近似であるため、D_{KL}(\pi_{\theta_{\text{old}}} \parallel \pi_{\theta}) \approx \frac{1}{2} (\theta - \theta_{\text{old}})^{\top} H(\theta_{\text{old}}) (\theta - \theta_{\text{old}})となります。つまり、HはKL Divergenceのヘッシアンです。
あとは式(6)で表された問題を頑張って解けば以下のような\thetaに関する更新式が求まります。
\begin{equation}
\theta_{\text{new}} = \theta_{\text{old}} + \sqrt{\frac{2\delta}{g^\top H^{-1} g}} H^{-1} g
\end{equation}
実際にはこのあとに線形探索などもして最適化ステップをみつけるということをするがここでは省略します。ここでナイーブなPolicy GradientとTRPOの\thetaの更新式の違いを見てみましょう。TRPOの更新式を\theta_{\text{old}}=\theta_i, \quad \theta_{\text{new}} = \theta_{i+1}で書き直すと
\theta_{i+1} = \theta_i + \alpha \nabla J(\theta) \qquad \text{(Policy Gradient)} \\
\theta_{i+1} = \theta_{i} + \sqrt{\frac{2\delta}{g^\top H^{-1} g}} H^{-1} g \qquad \text{(TRPO)}
これをみると\thetaの更新式から固定値のalphaが消えて、閾値の\deltaでステップサイズが決まっているのが見えますね!もう少し直感的なイメージとしては、TRPOを信頼領域とよばれる領域を作り、\thetaをその中で最適化するように更新していくという感じになります。この信頼領域の大きさを決めるのがパラメータ\deltaとなるわけです。
CPOが解く問題の定式化
1. CPOのMotivation
TRPOは勾配降下法の一つで安定した学習を達成し良い方策を得ることができますが、まだ問題は残っています。それは安全制約などの制約をかけられないということです。TRPOはKL Divergenceを制約として持っていますが、これはあくまでも2つの方策が離れないようにする制約で学習環境に由来する制約ではありません。ただ、実世界の問題では障害物回避や入力値制限などの制約がある中で報酬を最大化する方策を求めたいことがほとんどです。これを解けるように提案されたのがTRPOの続編(進化版)とも言えるConstrained Policy Optimizaiton(CPO)になります。CPOは以下の最適化問題を解くこと目指しています。
\begin{equation}
\begin{split}
\underset{\theta}{\operatorname{max}} \quad &J(\pi_{\theta}) \\
\text{subject to} \quad &D (\pi_{\theta_{old}}(\cdot|s_i), \pi_{\theta}(\cdot|s_i)) \leq \delta \\
& J_{C_i}(\pi_{\theta}) \leq d_i \qquad (i=1, 2, \cdots, m)
\end{split}
\end{equation}
ここでJ_{C_i}はi番目の制約式でmは制約の数になります。以下ではこの式の解き方についてCPOで提案されている手法を解説していきます。なお最後に、今後の説明の簡易化のために以下にdiscounted future state distributionを定義します。
d_\pi (s) = (1-\gamma) \sum_{t=0}^{\infty} \gamma^t P(s_t=s|\pi)
これは方策\piとダイナミクスモデルp(\cdot|s`,a)に従ったときに状態sにいる確率と解釈できます。また、discounted(割引)となっているのはtが大きくなるにつれて\gamma^t p(s_t=s)とすることで未来の時間のstate distributionの影響を小さく(割り引いている)しているからです。
2. 最適化問題(8)の問題と解決法
Constrained Policy Optimization(CPO)は制約付きのMDPを近似して解くための手法です。もっと具体的にいうと(8)で表された最適化問題を近似して解く手法です。
まず最適化問題(8)を解くのが難しい理由を考えてみます。なぜこの問題を直接解くのが難しいのでしょうか。答えは2番目の制約式にあります。
J_{C_i}(\pi_{\theta}) \leq d_i
こちらの制約式ですが、新しい方策\pi_\thetaに対する制約になっています。問題は\pi_{\theta}が通常は非常に複雑な形をしており(NNなどで近似をされているため)、また関数J_{C_i}もかなり複雑な形をしていることが多いため、J_{C_i}(\pi_{\theta})を解きやすい形で書き下すのがかなり難しいことが分かります。この問題を解決するためにCPOでは
(8)の最適化問題の目的関数と2つめの制約J_{C_i}を別の関数で近似をして解く。
というアプローチをとります。これがCPOのアルゴリズムで一番大事な点になります。実はこのアイデアはTPROと同じです。つまり、難しい最適化問題をそのまま解くのではなくて、目的関数や制約を他の関数を使って表して最適化するということです。元論文ではこの代わりの関数のことを代理関数(surrogate function)と呼んでいます。CPOの中で提案されている代理関数は元の問題(8)の最悪ケースをboundできるようにえらばれています。つまり、代理関数を使って最適化して得られた\pi_{\theta}はどんなに近似が悪くても元の問題の目的関数を大きく悪くすることはなく、また制約を大きく逸脱するということもありません。ただ、今回の記事では具体的な代理関数の選び方やそれがワーストケースをboundできるという説明はしません。こちらはかなり長くなるので別記事で紹介します。
3. 新しい最適化問題
さて、代理関数を使って表された新しい最適化問題は以下のように表されます。
\begin{equation}
\begin{split}
\underset{\theta}{\operatorname{max}} \quad & \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}, a\sim \pi_{\theta}} \left[ A_{\pi_{\theta_{\text{old}}}} (s,a) \right] - \alpha_k \sqrt{\overline{D_{KL}}(\pi_{\theta} || \pi_{\theta_{\text{old}}})} \\
\text{subject to} & \quad J_{C_i}(\pi_{\theta_{\text{old}}}) + \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}, a\sim \pi_{\theta}} \left[\frac{A_{\pi_{\theta_{\text{old}}}}^{C_i}}{1-\gamma} \right] + \beta_k^i \sqrt{\overline{D_{KL}}(\pi_{\theta} || \pi_{\theta_{\text{old}}})} \leq d_i \qquad (i=1, 2, \cdots, m)
\end{split}
\end{equation}
ここで\alpha_kと\beta_k^iはパラメータで\pi_\thetaと\pi_{\theta_{\text{old}}}が大きく離れないようにするためのpenalty関数の係数であり、\overline{D_{KL}}はKL divergenceを状態sに対して期待値を取ったもので以下のように定義される。
\overline{D_{KL}}(\pi_{\theta} || \pi_{\theta_{\text{old}}}) = \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}} \left[ D_{KL} (\pi_{\theta_{old}}(\cdot|s) || \pi_{\theta}(\cdot|s) \right]
この最適化問題(9)は\pi_\thetaを更新するにつれてパフォーマンスが上がることを保証しており、また、適切な\beta_k^iを選べば元の制約J_{C_i}(\pi_\theta) \leq d_iも守るようになっています。詳細は別記事で示しますが、この最適化問題の制約の左辺はもとのJ_{C_i}の上限値になっています。
CPOはこの(9)で表された最適化問題を解いていくのですがまだこの定式化には欠点があります。この式には\pi_\thetaと\pi_{\theta_{\text{old}}}が大きく離れないようにするためのpenalty関数が入っているのですが、これを使ってしまうことで更新ステップを小さくしないとうまく最適化できないという理由があります。特に割引率の\gammaが1に近いときにKL divergenceによる勾配がかなり深くなるため、更新ステップをかなり小さくしないと\thetaが大きく変更されてしまい学習が不安定化しています。そのためCPOではTRPOと同じテクニックを使い、penalty法でなくて代わりにKL divergenceのハード制約をつけることでこの問題を解消していきます。この手法は信頼領域(trust region method)と同じになります。
\begin{equation}
\begin{split}
\underset{\theta}{\operatorname{max}} \quad & \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}, a\sim \pi_{\theta}} \left[ A_{\pi_{\theta_{\text{old}}}} (s,a) \right] \\
\text{subject to} & \quad J_{C_i}(\pi_{\theta_{\text{old}}}) + \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}, a\sim \pi_{\theta}} \left[\frac{A_{\pi_{\theta_{\text{old}}}}^{C_i}}{1-\gamma} \right] \leq d_i \qquad (i=1, 2, \cdots, m) \\
&\quad \overline{D_{KL}}(\pi_{\theta} || \pi_{\theta_{\text{old}}}) \leq \delta
\end{split}
\end{equation}
ここで\deltaはパラメータで\pi_\thetaと\pi_{\theta_{\text{old}}}がどれくらい離れていいか決める指標になります。しかし、残念ながらこの新しい最適化問題(10)を解くことで得られる方策\pi_{\theta}は元の制約J_{C_i}(\pi_\theta) \leq d_iを守る保証がありません。ただし、最悪の場合の制約違反値を求めることは可能で以下のような等式が成立します(証明は別記事)。
J_{C_i}(\pi_{\theta_{\text{new}}}) \leq d_i + \frac{\sqrt{2\delta}\gamma \epsilon_i^{\pi_{\theta_{\text{new}}}}}{(1-\gamma)^2}
ここで\epsilon_i^{\pi_{\theta_{\text{new}}}} = max_s|E_{a\sim \pi_{\theta_{\text{new}}}} \left[ A_{C_i}^{\pi_{\theta_{\text{old}}}}(s,a) \right]|である。つまり、(10)式で求まった方策はオリジナルの制約より\frac{\sqrt{2\delta}\gamma \epsilon_i^{\pi_{\theta_{\text{new}}}}}{(1-\gamma)^2}だけオーバすることがある。もっと言うと、CPOを使ってといて得られた方策は制約条件をまもれないことがあるということである。
CPOのアルゴリズム詳細
1. CPOを使って(10)をどうやって解くか
さて、(10)でCPOが解いていく最適化問題がわかったのですが、これをソルバーなどにはまだ突っ込めません。なぜなら目的関数と制約がまだよくわからない非線形で解きにくいからです。CPOではここからまず目的関数と制約J_{C_i}を線形化、KL divergence制約を2次近似していきます。この流れはTRPOとほぼ一緒ですね!近似した最適化問題は以下のようになります。
\begin{equation}
\begin{split}
\underset{\theta}{\operatorname{max}} \quad & g^\top(\theta - \theta_{old})\\
& c_i + b_i^{\top}(\theta - \theta_{\text{old}}) \leq 0 \qquad (i=1, \cdots, m) \\
& \frac{1}{2} (\theta - \theta_{\text{old}})^{\top} H (\theta - \theta_{\text{old}}) \leq \delta
\end{split}
\end{equation}
g_i = \nabla_{\theta} \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}, a\sim \pi_{\theta}} \left[ A_{\pi_{\theta_{\text{old}}}} (s,a) \right]、HはKL divergenceのヘッシアン、c_i=J_{C_i}(\pi_{\theta{\text{old}}})-d_i、そしてc_iは一つめの制約のgradientとなり
\nabla_{\theta} \mathbb{E}_{s \sim d_{\pi_{\theta_{\text{old}}}}, a\sim \pi_{\theta}} \left[\frac{A_{\pi_{\theta_{\text{old}}}}^{C_i}}{1-\gamma} \right]
と書けます。また、(11)の最適化問題は凸最適問題になっています。理由としては目的関数が線形で制約の1つ目も線形、そしてKL DivergenceのHessianはフィッシャーの情報行列になるため制定値であることから示せます。これで解きやすい形になったので(11)の最適化問題を解けば終了と言いたいところですが実はここはもうひと工夫できます。
2. (11)式の双対問題
実は(11)の最適化問題ですが最適変数が方策のパラメータの\thetaになっています。これ、なにが問題かというと、ニューラルネットワークなどを使って方策\pi_{\theta}を表したときにパラメータ数がものすごい数になり、計算に時間がかかるという欠点があります。対して(11)の問題の制約の数は多くの場合、パラメータの数よりも少ないことが多いです。なお、(11)の凸最適問題の制約数はm+1です。このような場合、双対問題を主問題の変わりに解くことで少ない最適化変数で効率的に問題をとくことができます。また、今回は凸最適化問題なので双対問題の最適解と主問題の最適解が一致することが保証されます。双対問題の導出はこの記事の最後にします。
B=[b_1, \cdots, b_m], c=[c_1, \cdots, c_m]と定義して、以下の(11)の双対問題の最適化をしていきます。
\begin{equation}
\underset{\lambda \geq 0, \hspace{1mm} \nu \geq 0}{\operatorname{max}} \quad \frac{-1}{2 \lambda}(g{\top}H^{-1}g - 2r^{\top} \nu + \nu^{\top} S \nu) + \nu^{\top}c - \frac{\lambda \delta}{2}
\end{equation}
ここで\nuと\lambdaは双対変数で、r=g^{\top}H^{-1}B、S=B^{\top}H^{-1}Bです。あとはこのシンプルな2次形式の問題を解けばよいだけです。最適化問題をといて得られた最適解を\lambda^{*}と\nu^{*}と書くと主変数\thetaの更新式は次のように表せます。
\begin{equation}
\begin{split}
\theta_{i+1} &= \theta_i + \frac{1}{\lambda^{*}}H^{-1}(g-B\nu^{*}) \\
&= \theta_i + \frac{1}{\lambda^{*}}H^{-1}g - \frac{1}{\lambda^{*}}H^{-1}B \nu^{*} \qquad \text{(CPO)}
\end{split}
\end{equation}
Policy GradientとTRPOの更新式もここに再掲しておきます。
\theta_{i+1} = \theta_i + \alpha \nabla J(\theta) \qquad \text{(Policy Gradient)} \\
\theta_{i+1} = \theta_{i} + \sqrt{\frac{2\delta}{g^\top H^{-1} g}} H^{-1} g \qquad \text{(TRPO)}
こうみると、CPOはTRPOと同じ方向H^{-1}gに更新していますが、制約を含んでいるためH^{-1}B \nu^{*}の方向にも更新しないといけないことが分かります。
3. 細かい実装について
ここでは細かい実装の詳細について述べておきます。ただ、ほとんどはTRPOと同じやり方です。
- 上記の更新式だと新しい方策\pi_{\theta_{i+1}}が元の最適化問題(10)の制約を満たさない可能性があるので実際には(10)の制約を満たすまで線形探索を行います。\kappa \in [0, 1]としてこの\kappaを制約が満たすまでどんどん小さくしていきます。
\theta_{i+1} = \theta_i + \kappa \frac{1}{\lambda^{*}}H^{-1}(g-B\nu^{*})
-
\thetaの更新時にH^{-1}の計算をしないといけないのですがこの計算が非常に重たいため可能な限り避けたいです。更新式をみると我々が求めたいのはH^{-1}ではなくてH^{-1}gやH^{-1}b_iなのでH^{-1}を求める必要はなく、このヘッシアンHの逆行列とベクトルの積を求めればいいことが分かります。この計算は共役勾配法を使って効率的に求めることができます。この部分の計算は他のTRPOの解説記事が詳しく書いているのでそちらに譲ります。
-
CPOは線形探索などをして頑張って制約を守れるようにしていますが、それでも制約を守りきれない方策\pi_\thetaが出てくることがあります。その場合は以下の問題を解いて\thetaを更新して制約を守れるようにします。なお以下は制約が一つしかない場合の計算式です(B=b)。この式をみるとH^{-1}b=H^{-1}Bの方向に\thetaを動かすことで制約を守れるように変化させていることが分かります。この方向は式(13)の式の一部にも現れていました。
\begin{equation}
\theta_{i+1} = \theta_i - \sqrt{\frac{2\delta}{b^{\top}H^{-1}b}} H^{-1}b
\end{equation}
最後に全体のアルゴリズムの流れを示しておきます(元論文の数式と同じ数式番号になるようにこの記事を書いています)。

[まとめ]最適化問題の全体の流れ
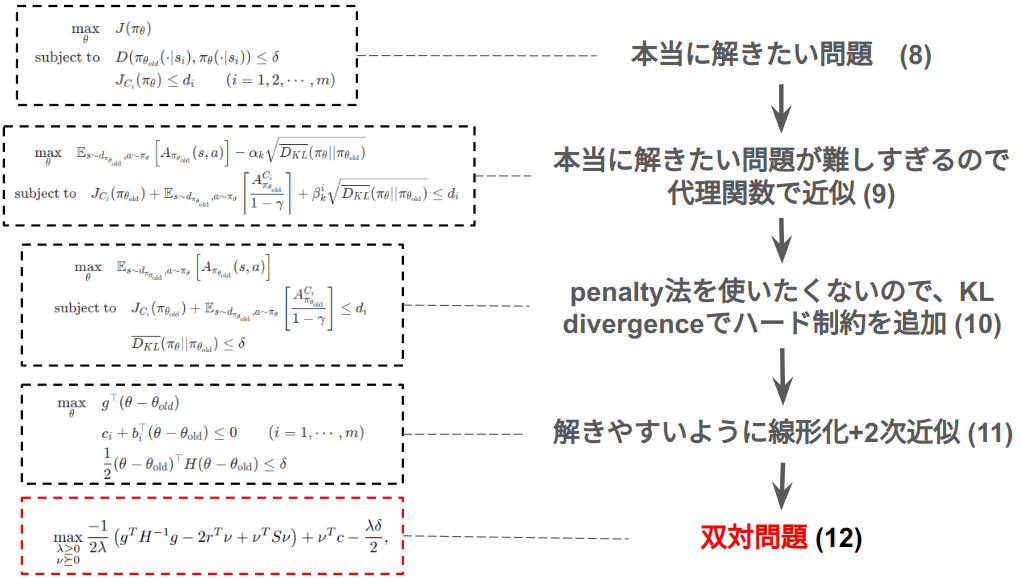
以上でCPOの説明は終わりますが、CPOがわかりにくい一因として結局どの問題を最適化しているのかがわからないというのがあります。以下の図にCPOが解きたい問題の流れを載せました。本当に解きたい問題(8)から出発して、代理関数による近似(9)、信頼領域法への転換(10)、線形化+2次化(11)、そして最終的に解いていく双対問題(12)という流れになります。この全体の流れとどうして各変形をやっているのかという点を押さえればCPOの理解が1段階進むと思います。
おわりに
ここまでCPOの大きな流れやポイントについて話してきました。CPOを制約付きの強化学習問題を解ける枠組みのひとつになっています。ただ、記事の中でも示したようにCPOは本当に守りたい制約J_{C_i}(\pi) \leq d_iを守ることを保証できていません。あくまでも最適化問題(10)で書いた制約しか守れません。そのため、本当に制約付きの最適化問題を解きたいケースに対してはもう一歩踏み込んだ理論や計算が必要になります。
またCPOもTRPOと同じく、最適化数学から様々な手法を使っています。双対問題などもでてくるため最適化数学に対する深い理解や知見がないとかなり理解しにくい手法にもなっています。
[おまけ]双対問題(12)の導出
最後になりましたが双対問題(12)の導出方法をこちらに書き記しておきます。なお最適化数学の知識がかなり問われるため、まだ双対問題やラグランジュ関数などに関してあまり詳しくない方はそちらに関連する記事などを見てからこちらに戻ってくるとより理解しやすいかもしれません。
[執筆中]


Discussion