CosFace・ArcFaceとElasticFaceへの拡張

はじめに

最近深層距離学習が気になっており、いろいろ勉強する日々を送っています。
そんな中、過去のKaggleなどの画像系コンペでElasticFaceを用いた解法を時折見かけ、試してみよ〜と思ったのですが、意外に日本語の解説記事等がなかったので備忘録的に書き起こしておこうと思います。
元論文はこちら

CosFace・ArcFace

CosFace・ArcFaceはサーベイ論文で名を挙げられるほど強力な角度系距離学習の1つです。
「とりあえず使える」という部分もさることながら、直感的に理解できる部分もポイントが高いです。

式

• Cosface

$$-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp (s \cos (\theta_{y_i}) - m)}{\exp (s \cos (\theta_{y_i}) - m) + \sum_{k \neq y_i} \exp (s \cos \theta_k)}.$$

• Arcface

$$-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp (s \cos (\theta_{y_i} + m))}{\exp (s \cos (\theta_{y_i} + m)) + \sum_{k \neq y_i} \exp (s \cos \theta_k)}.$$

一見すると「どこが違うん..?」となるくらいかなり似た式ですが、分母分子の$cos(θ_{yi})$の部分が違い、具体的にはマージン$m$の制約の掛け方が違います。

違いの解説

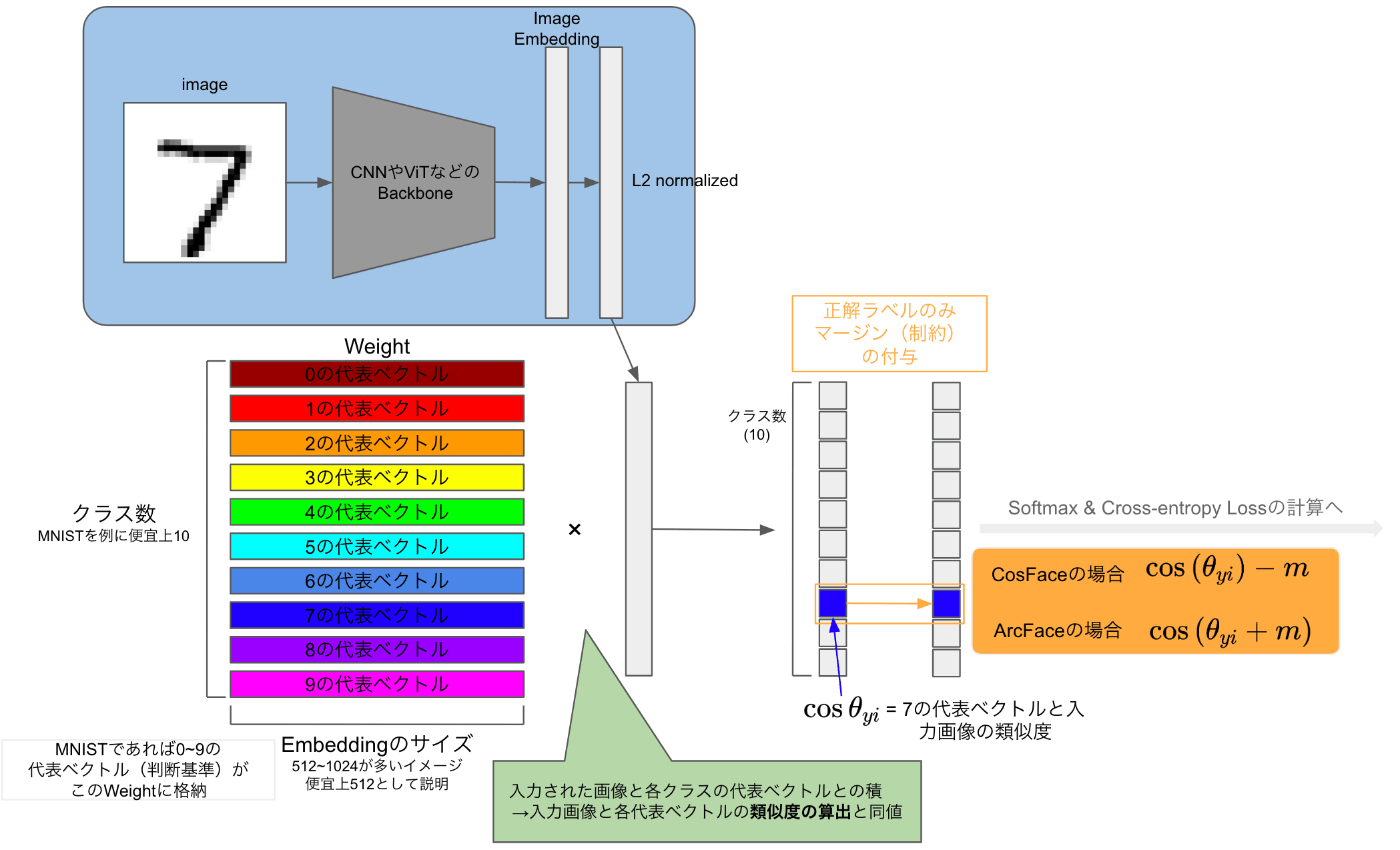
上図の流れとして、

1. CNNやViTなどの特徴量抽出器に画像を入力し、画像ベクトルに変換し、$L2$正規化を行う。
2. 取得した入力画像ベクトルを各クラスの代表ベクトル（最後にちょっと解説）の積を計算する。これにより、入力画像ベクトルと各代表ベクトルとのそれぞれのコサイン類似度を計算していることになる。

ここまではCosFaceもArcFaceも同じ流れですが、前述した通りその後の「マージン付与」の方法が違います。
CosFaceは上で紹介した通り、$cos(θ_{yi})+m$となり、入力画像ベクトルと各クラスの代表ベクトルとの計算後のコサイン類似度自体に制約を入れます。
それに対し、ArcFaceは$cos(θ_{yi}+m)$は、入力画像ベクトルと各クラスの代表ベクトルのなす角に制約をいれ、その結果としてコサイン類似度の値が変化します。

まとめると

• CosFace: 類似度の値自体に制約を付与
• ArcFace: なす角度に制約を付与し、結果的に類似度の値に影響を与える

CosFaceもArcFaceもマージンを与えるという点では同じで、効果としてはクラス内の散らばりを小さくし、他のクラスとの角度（類似度）を遠ざけることが期待できます。

ElasticFace

次にElasticFaceの説明ですが、まず元論文で解説されているCosFaceやArcFaceの問題点について着目していきます。

CosFace・ArcFaceの問題点

元論文では以下のように解説されています。

Even though, ArcFace [4], CosFace [27] and SphereFace [16] introduced the important concept of angular margin penalty on softmax loss, selecting a single optimal margin value (α) is a critical issue in these works. By setting up m1 = 1, m2 = 0 and m3 = 0, ArcFace, CosFace and SphereFace are equivalent to the modified softmax loss. A reasonable choice could be selecting a large margin value that is close to the margin upper bound to enable higher separability between the classes. However, when the margin value is too large, the model fails to converge, as stated in [27]. ArcFace, CosFace, and SphereFace selected the margin value through trial and error assuming that the samples are equally distributed in geodesic space around the class centers. However, this assumption could not be held when there are largely different intra-class variations leading to less than optimal discriminative feature learning, especially when there are large variations between the samples/classes in the training dataset.

ここではCosFace・ArcFace、そして今回紹介していませんが、マージンの付与の種類が別のSphereFaceは前述の通り、マージンという重要な概念を導入しています。マージンはハイパーパラメーターで、最適な値であることが重要な問題として考えており、その上でどのような値を取れば良いのか？という部分での難しさと、実際のデータセットのサンプル・クラス内のばらつきが大きい場合に最適な学習ができないのではないかと示唆しています。
また、ArcFaceやCosFaceはマージンが固定の値$m$を利用しており、この固定の値で学習ができることを仮定していますが、実際のデータはクラス間及びクラス内の一貫性のない、ばらつきがあると考え、そのような仮説は現実的ではなく、特に顔認識モデルの識別性と汎化性を制限する可能性があるとしています。

ElasticFaceが提案する手法

式

同じようにまずは式を見てみましょう。

• ElasticFace-Cos(ElasticFaceをCosFaceに適用)

$$-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp (s \cos (\theta_{y_i}) - E(m, \delta))}{\exp (s \cos (\theta_{y_i}) - E(m, \delta)) + \sum_{k \neq y_i} \exp (s \cos \theta_k)}.$$

• ElasticFace-Arc(ElasticFaceをArcFaceに適用)

$$-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp (s \cos (\theta_{y_i} + E(m, \delta)))}{\exp (s \cos (\theta_{y_i} + E(m, \delta))) + \sum_{k \neq y_i} \exp (s \cos \theta_k)}.$$

両式の$E(m, \delta)$は平均$m$標準偏差$\delta$に従う正規分布から抽出した値という意味です。
また$m$と$\delta$についてはハイパーパラメータであるため、指定する必要があります。

既存手法からの改善点

既存のCosFace・ArcFaceと違う点は、マージンを確率分布に従った乱数を用いているという点です。
これにより以下の効果が期待できるとされています。

1. マージン制約の緩和による柔軟性の向上
   トレーニング時の各イテレーションで正規分布から抽出されたランダムなマージン値を使用することで、クラスの分離性を向上させる柔軟性が獲得できるとされています。

2. 実データの変動への対応
   固定のマージンでは対応できなかった実データの変動、例えば、人の顔の特徴や環境、撮影条件など様々な変動が存在しますが、ランダムなマージン値によってこのような変動に柔軟に対応することができることを目的としています。

3. 難しく分類されるサンプルへの注目
   他のサンプルより識別が難しいサンプルが含まれることが往々にあり、これらの「難しい」サンプルに対して固定のマージン値を使用すると適切に学習されないことがあります。これに対しElasticFaceでは、このようなほとんど分類されないようなサンプルに対してより多くの注意を払うこととができるようにするためにランダム性を導入したとしています。

既存手法とマージンの適用の違い

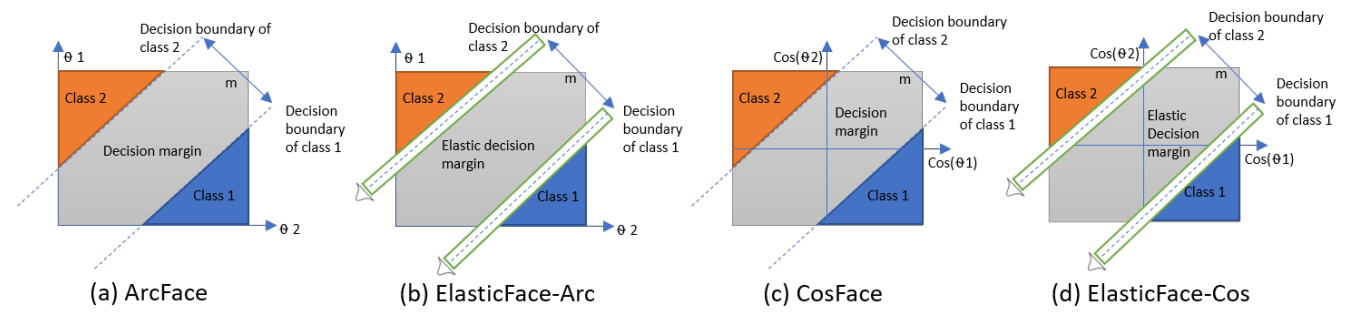
元論文の比較画像です。
(a)(c)は既存手法であるArcFace、CosFaceで、(b)(d)はElasticFaceへの拡張版です。
前述した通り、既存手法と比べて、境界線の引き方に違いがあり、緑の枠内でのランダムな境界線の引き方になります。

ElasticFace+

さらなる拡張手法として、＋をつけたElasticFace＋についても提案されています。
これはランダムなマージン値の適用に加えて、トレーニング時の各イテレーションのクラス内の変動を観察した上で、各サンプルに対してマージンを適用します。
もう少し踏み込んで説明すると、無印ElasticFaceでは正規分布から抽出したマージンを適当に適用するのに対し、ElasticFace+では各クラスの代表ベクトルと入力画像とのコサイン類似度の値の高さに応じてマージンを適用する方法を変えているのです。
実装を見ることでさらにわかりやすくなると思います。

ElasticFace+の実装について

元論文で紹介されているGitHubの実装を元に解説します。またこちらではElasticFace-Arc+について説明します。

class ElasticArcFace(nn.Module):
    def __init__(self, in_features, out_features, s=64.0, m=0.50,std=0.0125,plus=False):
        super(ElasticArcFace, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.s = s
        self.m = m
        self.kernel = nn.Parameter(torch.FloatTensor(in_features, out_features))
        nn.init.normal_(self.kernel, std=0.01)
        self.std=std
        self.plus=plus
    def forward(self, embbedings, label):
        embbedings = l2_norm(embbedings, axis=1)
        kernel_norm = l2_norm(self.kernel, axis=0)
        cos_theta = torch.mm(embbedings, kernel_norm)
        cos_theta = cos_theta.clamp(-1, 1)  # for numerical stability
        index = torch.where(label != -1)[0]
        m_hot = torch.zeros(index.size()[0], cos_theta.size()[1], device=cos_theta.device)
        margin = torch.normal(mean=self.m, std=self.std, size=label[index, None].size(), device=cos_theta.device) # Fast converge .clamp(self.m-self.std, self.m+self.std)
        if self.plus:
            with torch.no_grad():
                distmat = cos_theta[index, label.view(-1)].detach().clone()
                _, idicate_cosie = torch.sort(distmat, dim=0, descending=True)
                margin, _ = torch.sort(margin, dim=0)
            m_hot.scatter_(1, label[index, None], margin[idicate_cosie])
        else:
            m_hot.scatter_(1, label[index, None], margin)
        cos_theta.acos_()
        cos_theta[index] += m_hot
        cos_theta.cos_().mul_(self.s)
        return cos_theta

重要なのはforward()内のif self.plus:内の実装です。中身を見てみましょう。

distmat = cos_theta[index, label.view(-1)].detach().clone()

distmatは入力画像と各クラスの代表ベクトルとのコサイン類似度で、これをコピーしてきます。

_, idicate_cosie = torch.sort(distmat, dim=0, descending=True)

取得してきたコサイン類似度をソートし、コサイン類似度を降順にします。idicate_cosieにはソート前の元の位置のインデックスが格納されています。

margin, _ = torch.sort(margin, dim=0)

事前に正規分布から抽出したランダムなマージンの値もソートします。こちらは昇順です。

m_hot.scatter_(1, label[index, None], margin[idicate_cosie])

予め用意したm_hotの特定の場所にマージンを配置します。

cos_theta.acos_()
cos_theta[index] += m_hot
cos_theta.cos_().mul_(self.s)
return cos_theta

最後にcos_theta.acos_()でコサイン類似度から角度$\theta$に変換し、cos_theta[index] += m_hotで$\theta + m$を計算し、cos_theta.cos_().mul_(self.s)で$s(cos(\theta + m))$を計算している、という流れになります。

コサイン類似度とマージンをソートしている部分がありましたが、ここがElasticFace+の特徴的な部分で、コサイン類似度が高ければ少ないマージンを、コサイン類似度が低ければ高いマージンを付与する動きになっています。コサイン類似度とマージンでそれぞれで降順と昇順になっていたのはこれが理由です。

「コサイン類似度が低ければ高いマージンを適用する」この動きによって、モデルが分類を「難しい」とするサンプルを正しく分類できるようにするため誘導することができます。
逆の「コサイン類似度が高ければ少ないマージンを適用する」ことで、モデルが分類を「易しい」とすると考えられるため、これらのサンプルに過度にマージンを調節することなく、より分類が「難しい」サンプルに焦点を当てることができるのですね。賢すぎです。

感想

私もこの記事を書きながらさらに理解を深めましたが、理解すればするほど「これ考えた人天才か？」とばかり思いました😂
この記事が深層距離学習を勉強するあなたの参考になれば嬉しいです。

Appendix クラスの代表ベクトルについて

私は最初見たときなぜこれがあるのか？と思いました。もしかしたら同じ方がいらっしゃるかもしれないので私の認識を比喩で例えてみようと思います。

例えば、皆さん「猫」と「犬」を判断するときに何を基準にされていますか？具体的に耳のサイズがこんな感じ！とか鼻の形がこんな感じ！みたいに判断される方はおそらくいないと思います。

おそらくですが、皆さんの頭の中にそれぞれ「猫」「犬」が存在し、実際に猫または犬を見た際に、自分が知っている「猫」「犬」のどちらに近いか？という操作を無意識に脳内で行っていると思われます。
その頭の中の「猫」「犬」が今回の「代表ベクトル」というものなのかな？と認識しています。
なので、見たことないような猫だったり犬がいたら「こういうのもいるんか」と頭の中の「猫」「犬」の情報を修正すると思いますが、まさしくこの操作をArcFace系で行っているということです。（異論は認めます。皆さんのご意見も聞いてみたいです。）