Bloch関数の局在関数ーWannier関数ーを用いた展開

はじめに

前章でBloch関数、そしてBlochの定理という形で、固体中の電子の波動関数が満たすべき関数形、そしてその性質を理解しました。本章ではそこで得られた結果をもう少し変形し、固体中の電子状態を表すことができる関数を別の形で表現します。
初めに、前章で得られた内容を振り返っておきます。

前章の振り返り

前章でBlochの定理を示し、固体中の電子の波動関数はBloch波数$\boldsymbol{k}$を代表とし、それと逆格子ベクトル$\boldsymbol{K}$だけ異なるFourier成分で展開される関数$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})$：

$$\begin{align*} \varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) &= \frac{1}{\sqrt{V}}\sum_{\boldsymbol{K}}c_{\boldsymbol{k} - \boldsymbol{K}}e^{i(\boldsymbol{k} - \boldsymbol{K})\cdot\boldsymbol{r}}\\ &= e^{i\boldsymbol{k}\cdot\boldsymbol{r}}u_{n,\boldsymbol{k}}(\boldsymbol{r}) \end{align*}$$

で表されることが分かりました。2式目の$u_{n,\boldsymbol{k}}(r)$は、格子の基本併進ベクトル$\boldsymbol{a}_i$の周期を持つ周期関数です。
また逆格子ベクトル$\boldsymbol{K}$は、

$$\begin{align*} \boldsymbol{K} &= m_1\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)} + m_2\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)} + m_3\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}\\ &\equiv m_1\boldsymbol{b}_1 + m_2\boldsymbol{b}_2 + m_3\boldsymbol{b}_3 \end{align*}$$

で定義されるベクトルです。例によって逆格子ベクトルであることを強調する意味で大文字の$\boldsymbol{K}$で書きます。上式2式目で定義した$\boldsymbol{b}_i$は、それぞれ基本併進ベクトル$\boldsymbol{a}_i$の双対ベクトルと呼ばれるもので、$\boldsymbol{a}_i\cdot\boldsymbol{b}_j = 2\pi\delta_{ij}$を満たします。

また上記のように表したとき、ブロッホ関数$\varphi_{n,\boldsymbol{k}}$は格子ベクトル$\boldsymbol{n} = n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3, n_i = 0,\pm 1, \pm 2\cdots$に対して

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r} + \boldsymbol{n}) = e^{i\boldsymbol{k}\cdot\boldsymbol{n}} \varphi_{n,\boldsymbol{k}}(\boldsymbol{r})$$

を満たします。

Bloch関数の実空間での形

さて、ここでBloch関数は

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})= e^{i\boldsymbol{k}\cdot\boldsymbol{r}}u_{n,\boldsymbol{k}}(\boldsymbol{r})$$

として表されるように、固体中に広がった関数（固体中の周期関数$u_{n,\boldsymbol{k}}(\boldsymbol{r})$に、Bloch波数の平面波$e^{i\boldsymbol{k}\cdot\boldsymbol{r}}$が掛け合わされたもの）です。^[1]

一方本稿のゴールTight-binding近似（モデル）は、その名の通り強く格子ポテンシャルに束縛された状態を想定しており、格子点に局在した状態をもとに近似を考え始めたいわけです。そうすると上記のBloch関数のような広がった関数とは相性が悪そうです。

そこで本章では、Bloch関数についてもう少し考えを進めることで、Bloch関数が格子点に局在しているような状態（関数）の重ね合わせで表現できることを示します。この関数はTight-binding近似の出発点となるもので Wannier function（ワニエ関数） と呼ばれます。

Wannier関数の一般的定式化と性質

初めに、本節でBloch関数を実空間上の格子点の座標

$$\boldsymbol{R} = n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3$$

で指定される関数で展開することができることを示します。
なお、今までは格子ベクトルを$\boldsymbol{n}$で表していましたが、本章からは$\boldsymbol{R}$を使います。これは色々な教科書でそう書かれているからなのですが、気持ちとしては「格子点の集合」を表すときは$\boldsymbol{n}$を使って、格子点の座標を表すときはより座標っぽい$\boldsymbol{R}$を使うということなのかと思っていますが、あまり深く考えないことにします。とにかくここからは格子点の座標は$\boldsymbol{R}$です。

これがまさにWannier関数です。本節ではWannier関数の定式化と、その性質を示します。

また次節でこのWannier関数が実空間上の格子点に局在した関数であることを（定性的な議論になってしまうのですが）確かめます。

定式化：Bloch関数の展開

早速始めましょう。前章で示したように、Bloch関数はBloch波数$\boldsymbol{k}$について、逆格子ベクトル$\boldsymbol{K}$の周期を持つ逆格子空間上の周期関数として考えることができるのでした。
すなわちBloch波数$\boldsymbol{k}$に関して、

$$\varphi_n(\boldsymbol{r},\boldsymbol{k} + \boldsymbol{K}) = \varphi_n(\boldsymbol{r}, \boldsymbol{k})$$

を満たします。
ここで前章で

$$\begin{align*} \boldsymbol{k} &= m_1\frac{2\pi N_2\boldsymbol{a}_2\times N_3\boldsymbol{a}_3}{ N_1\boldsymbol{a}_1\cdot( N_2\boldsymbol{a}_2\times N_3\boldsymbol{a}_3)} + m_2\frac{2\pi N_3\boldsymbol{a}_3\times N_1\boldsymbol{a}_1}{ N_2\boldsymbol{a}_2\cdot( N_3\boldsymbol{a}_3\times N_1\boldsymbol{a}_1)} + m_3\frac{2\pi N_1\boldsymbol{a}_1\times N_2\boldsymbol{a}_2}{ N_3\boldsymbol{a}_3\cdot( N_1\boldsymbol{a}_1\times N_2\boldsymbol{a}_2)}\\ &= \frac{m_1}{N_1}\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)} + \frac{m_2}{N_2}\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)} + \frac{m_3}{N_3}\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)} \end{align*}$$

と定義したことを思い出し、$N_i\rightarrow\infty$とすれば$\boldsymbol{k}$は連続変数となることを踏まえてBloch関数を$\varphi_n(\boldsymbol{r}, \boldsymbol{k})$と書きました。

このことから、波数ベクトル$\boldsymbol{k}$の関数$\varphi_n(\boldsymbol{r}, \boldsymbol{k})$は、「逆格子ベクトルの逆格子ベクトル」

$$\begin{align*} \boldsymbol{G} &= l_1\frac{2\pi\boldsymbol{b}_2\times\boldsymbol{b}_3}{\boldsymbol{b}_1\cdot(\boldsymbol{b}_2\times\boldsymbol{b}_3)} + l_2\frac{2\pi\boldsymbol{b}_3\times\boldsymbol{b}_1}{\boldsymbol{b}_2\cdot(\boldsymbol{b}_3\times\boldsymbol{b}_1)} + l_3\frac{2\pi\boldsymbol{b}_1\times\boldsymbol{b}_2}{\boldsymbol{b}_3\cdot(\boldsymbol{b}_1\times\boldsymbol{b}_2)}\\ &\equiv l_1\boldsymbol{b}^*_1 + l_2\boldsymbol{b}^*_2 + l_3\boldsymbol{b}^*_3,\\ & l_i = 0, \pm 1, \pm 2 \cdots \end{align*}$$

を波数として持つ逆格子空間の平面波

$$e^{i\boldsymbol{G}\cdot\boldsymbol{k}}$$

を用いてFourier展開（平面波展開）

$$\varphi_n(\boldsymbol{r},\boldsymbol{k}) = \sum_{\boldsymbol{G}}C_{n,\boldsymbol{G}}(\boldsymbol{r})e^{i\boldsymbol{G}\cdot\boldsymbol{k}}, \\ C_{n,\boldsymbol{G}}(\boldsymbol{r})= \frac{1}{v_{BZ}}\int_{BZ} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{G}\cdot\boldsymbol{k}}d\boldsymbol{k}$$

することができる、と言えます。ここで2式目の積分は逆格子空間の単位胞、すなわちブリルアンゾーンを積分範囲として取ります。また$v_{BZ}$はブリルアンゾーンの体積$\boldsymbol{b}_1\cdot(\boldsymbol{b}_2\times\boldsymbol{b}_3)$です。

さて、ここで逆格子ベクトルの章で説明した通り、「逆格子ベクトルの逆格子ベクトル」は、元の実格子上の格子ベクトルと一致するのでした。すなわち、

$$\boldsymbol{b}^*_i = \boldsymbol{a}_i$$

です。これを先ほどの$\boldsymbol{G}$の定義に代入すると、

$$\begin{align*} \boldsymbol{G} &= l_1\boldsymbol{b}^*_1 + l_2\boldsymbol{b}^*_2 + l_3\boldsymbol{b}^*_3,\\ &= l_1\boldsymbol{a}_1 + l_2\boldsymbol{a}_2 + l_3\boldsymbol{a}_3 = \boldsymbol{R} \end{align*}$$

となります。つまり、任意のBloch関数$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})$あるいは$\varphi_n(\boldsymbol{r},\boldsymbol{k})$は、考えている固体の周期性に対応した格子ベクトル$\boldsymbol{R}$を用いて

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = \varphi_n(\boldsymbol{r},\boldsymbol{k}) = \sum_{\boldsymbol{R}}C_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}},\\ C_{n,\boldsymbol{R}}(\boldsymbol{r})= \frac{1}{v_{BZ}}\int_{BZ} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}d\boldsymbol{k}$$

と展開できることが分かりました。いやー、ややこしいですね。

Wannier関数の表現

さて、上記のようにBloch関数を展開しましたが、波数$\boldsymbol{k}$についての展開を考えていたことから、展開係数$C_{n,\boldsymbol{R}}$もまた、$\boldsymbol{r}$の関数となっており電子の観測確立に対応した波動関数的なものであると考えられます。このように定義された$C_{n,\boldsymbol{R}}(\boldsymbol{r})$を$w_{n,\boldsymbol{R}}(\boldsymbol{r})$と書き、この関数を提唱者の名前を取ってWannier関数と呼びます。改めて書くと、

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = \varphi_n(\boldsymbol{r},\boldsymbol{k}) = \sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}},\\ w_{n,\boldsymbol{R}}(\boldsymbol{r}) = \frac{1}{v_{BZ}}\int_{BZ} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}d\boldsymbol{k}$$

です。初めに述べたように、Wannier関数は実空間上の格子点の座標でラベルされます。

また、ここまで「$\boldsymbol{k}$は連続変数となる」としてきましたが、やっぱり離散変数と考えて積分を和で書き換えることもあります。この時実空間の単位胞の体積を$v_{cell}$、周期的境界条件の周期を$N = N_1N_2N_3$とし、その1周期分（つまり固体全体）の体積を$V = Nv_{cell}$として

$$\int_{BZ} d\boldsymbol{k}\rightarrow\frac{(2\pi)^3}{V}\sum_{\boldsymbol{k}\in BZ} = \frac{(2\pi)^3}{Nv_{cell}}\sum_{\boldsymbol{k}\in BZ}$$

となります。ここで$\sum_{\boldsymbol{k}\in BZ}$は（第1）ブリルアンゾーン内の$\boldsymbol{k}$について和を取ることを示します。さらにブリルアンゾーンの体積$v_{BZ}$が実空間の単位胞の体積$v_{cell}$を用いて

$$v_{BZ} = \frac{2\pi}{v_{cell}}$$

となることを用いて、Wannier関数の定義を

$$w_{n,\boldsymbol{R}}(\boldsymbol{r}) = \frac{1}{N}\sum_{\boldsymbol{k}\in BZ} \varphi_{n\boldsymbol{k}}(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}$$

と書くこともできます。

文献によっては$1/N$を2式に振り分けて、

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = \frac{1}{\sqrt{N}}\sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}},\\ w_{n,\boldsymbol{R}}(\boldsymbol{r}) = \frac{1}{\sqrt{N}}\sum_{\boldsymbol{k}} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}$$

と定義することもあります。（というかこちらの方が主流？）本稿ではこの後の話の展開の都合上、$w_{n,\boldsymbol{R}}(\boldsymbol{r})=\frac{1}{N}\sum_{\boldsymbol{k}} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}$の定義を採用しています。

また、上記1式目で表されているように、固体中の「広がった」電子状態を、各格子点で指定される関数$w_{n,\boldsymbol{R}}(\boldsymbol{r})$の線形結合によって表すことができるようになりました。元々のBloch関数の実空間上の関数を用いた表し方が

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = e^{i\boldsymbol{k}\cdot\boldsymbol{r}}u_{n,\boldsymbol{k}}(\boldsymbol{r})$$

と、周期関数$u_{n,\boldsymbol{k}}(\boldsymbol{r})$というヒントしかなかったところから、大きな進歩が得られました。

Wannier関数の性質

ここからもう少しWannier関数$w_{n,\boldsymbol{R}}(\boldsymbol{r})$の性質を確認していきます。

並進性

まず、格子の座標ラベル$\boldsymbol{R}$で指定されるWannier関数$w_{n,\boldsymbol{R}}(\boldsymbol{r})$が

$$w_{n,\boldsymbol{R}}(\boldsymbol{r}) =w_{n,0}(\boldsymbol{r}-\boldsymbol{R})\equiv w_{n}(\boldsymbol{r} - \boldsymbol{R})$$

と、座標の並進の形で書けることを確認します。これはBloch関数の逆格子ベクトル$\boldsymbol{K}$を用いた平面波展開

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = \frac{1}{\sqrt{V}}\sum_{\boldsymbol{K}}c_{\boldsymbol{k} - \boldsymbol{K}}e^{i(\boldsymbol{k} - \boldsymbol{K})\cdot\boldsymbol{r}}$$

を代入すれば良く、$e^{i(\boldsymbol{K}\cdot\boldsymbol{R})} = 1$を利用して、

$$\begin{align*} w_{n,\boldsymbol{R}}(\boldsymbol{r}) &= \frac{1}{v_{BZ}}\int_{BZ} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}d\boldsymbol{k}\\ &= \frac{1}{v_{BZ}}\int_{BZ} \frac{1}{\sqrt{V}}\sum_{\boldsymbol{K}}c_{\boldsymbol{k} - \boldsymbol{K}}e^{i(\boldsymbol{k} - \boldsymbol{K})\cdot\boldsymbol{r}} e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}d\boldsymbol{k}\\ &= \frac{1}{v_{BZ}}\int_{BZ} \frac{1}{\sqrt{V}}\sum_{\boldsymbol{K}}c_{\boldsymbol{k} - \boldsymbol{K}}e^{i(\boldsymbol{k} - \boldsymbol{K})\cdot\boldsymbol{r}} e^{-i(\boldsymbol{k} - \boldsymbol{K})\cdot\boldsymbol{R}}d\boldsymbol{k}\\ &= \frac{1}{v_{BZ}}\int_{BZ} \frac{1}{\sqrt{V}}\sum_{\boldsymbol{K}}c_{\boldsymbol{k} - \boldsymbol{K}}e^{i(\boldsymbol{k} - \boldsymbol{K})\cdot(\boldsymbol{r}-\boldsymbol{R})}\\ &= w_{n,0}(\boldsymbol{r}-\boldsymbol{R})\equiv w_n(\boldsymbol{r}-\boldsymbol{R}) \end{align*}$$

とわかります。

正規直交性

さらに、Bloch関数が正規直交することから^[2]
異なる格子の座標ラベル$\boldsymbol{R}$、バンドラベル$n$で指定されるWannier関数は以下のように正規直交します。

$$\begin{align*} \int_V w_{n'}^*(\boldsymbol{r}-\boldsymbol{R}')w_n(\boldsymbol{r} - \boldsymbol{R})dr &= \frac{1}{N^2}\sum_{\boldsymbol{k},\boldsymbol{k}'} e^{i\boldsymbol{k}'\cdot\boldsymbol{R}'}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}} \int_V \varphi_{n',\boldsymbol{k}'}^*(\boldsymbol{r}) \varphi_{n,\boldsymbol{k}}(\boldsymbol{r})d\boldsymbol{r}\\ &= \frac{1}{N^2}\sum_{\boldsymbol{k},\boldsymbol{k}'} e^{i\boldsymbol{k}'\cdot\boldsymbol{R}'}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}} N\delta_{n,n'}\delta_{\boldsymbol{k}, \boldsymbol{k}'}\\ &= \frac{1}{N}\delta_{n,n'}\sum_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R}'-\boldsymbol{R})}\\ &= \delta_{n,n'}\delta_{\boldsymbol{R},\boldsymbol{R}'} \end{align*}$$

局在性

以上から、Wannier関数$w_{n,\boldsymbol{R}}(\boldsymbol{r}) = w_n(\boldsymbol{r}-\boldsymbol{R})$は

• 格子点$\boldsymbol{R}$で指定されかつ原点の関数$w_n(\boldsymbol{r})$がラベルとなる格子点の座標$\boldsymbol{R}$で平行移動されたような関数
• 各格子点で指定されるWannier関数は直交している

という性質があることが分かりました。そこでWannier関数は、各格子点に局在したような関数であることが期待できそうです。

そこで最後に、最も物理的なイメージを想起させる局在性について述べたい、、ところなのですが、残念ながら（？）局在性についての一般的な導出が私は分かりません。^[3]

手元のアシュクラフト・マーミン^[4]によると、こちらの論文^[5]等でその辺が議論されているそうなのですが、またしても残念ながら私はこちらにアクセスできませんので、一旦は局在性についての一般的な議論をあきらめ、節を改めて（本節は「一般的な」と銘打っているので）定性的に確認するにとどめることとします。自由に論文を閲覧できる恵まれた環境におられる方は、良ければ確認してみて 、良いことが書いてあれば私にpdfをこっそり送って 下さい。

Wannier関数の局在性についてのイメージ

さて、上節では断念した局在性についての説明ですが、本節では一般性は無いですが、Wannier関数が実空間上で局在した関数であることを確認していこうと思います。

波束を用いた視覚的な確認

まずは格子点に局在してそうなイメージを視覚的に示してみます。特に、ラベル$\boldsymbol{R} = 0$の場合について確認できれば、それ以外のラベルで指定される関数はこの場合の平行移動なので、$w_{n,0}(\boldsymbol{r}) = w_n(\boldsymbol{r})$を考えていくことにします。
また、話を単純にするために1次元の場合を考えます。

格子点$0$で指定されるWannier関数はブロッホ関数を$\varphi_{n,k}(x)$として離散的な和で表すと

$$\begin{align*} w_n(x) &= \frac{1}{N}\sum_{k}\varphi_{n,k}(x)e^{-ik\times 0}\\ &= \frac{1}{N}\sum_{k}\varphi_{n,k}(x)\\ &= \frac{1}{N}\sum_{k}e^{ikx}u_{n,k}(x) \end{align*}$$

と書けます。ここで$k$の和の範囲ですが、BZでもいいのですが、波数空間の単位胞であればなんでも良いので（多分）、わかりやすく

$$k = \frac{2\pi}{Na}, \frac{2\pi}{Na}\times 2 \cdots, \frac{2\pi}{Na}\times N$$

を考えます。

さて、ここで$u_{n,\boldsymbol{k}}(\boldsymbol{r})$は具体的な形は分かりませんが、格子点の周期を持つ周期関数で、その周期関数に$k = \frac{2\pi}{Na}$から$k = \frac{2\pi}{a}$の平面波、つまり波長$\lambda = Na$の固体くらいの波長をもつ波から、波長$a$の格子点と同じくらいの波長を持つ波を掛け合わせた関数を足し合わせていくことになります。イメージとしては、

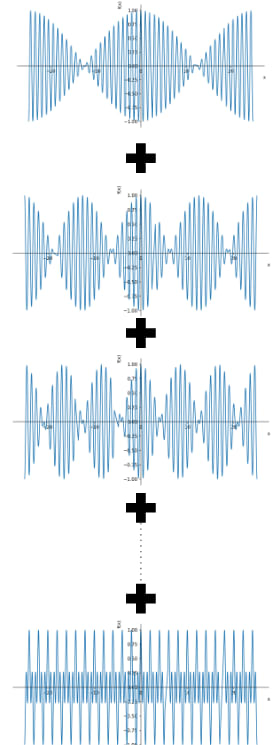
こんな感じ（正確には複素関数なので複素空間も書かないといけないのですが、まあイメージということで）。

すると原点以外は位相が異なる波数が次々足しあわされた結果、大体原点あたりのみ値が残りそれ以外の点は小さい、波束のような状態が得られそうな気がします。

具体的な関数を用いた確認

さて、上記ではあまりにも説明が雑な気もしつつ、もう少し具体的な関数を用いて確認することにします。

今度も1次元の場合を考え、またBloch関数として前章で「空格子モデル」として紹介した、平面波の場合を考えます。すなわち、

$$\varphi_{n,k}(x) = \frac{1}{\sqrt{Na}}e^{i(k-K_n)x}$$

を考えます。ただの平面波ですが、前章で確認したようにこれもBlochの定理を満たす、立派なBloch関数です（この場合、$u_{n,k}(x) =$（定数）に対応します）。この時ラベル$n$は逆格子ベクトル$K_n$に直接対応します。

さて、このBloch関数に対して$R = 0$のWannier関数を考えてみます。今度は先ほどと異なり積分で表示します。

$$\begin{align*} w_n(x) &= \frac{1}{v_{BZ}}\int_{BZ}\varphi_{n}(x,k)dk\\ &= \frac{1}{v_{BZ}} \int \frac{1}{\sqrt{Na}}e^{i(k-K_n)x} dk\\ &= \frac{1}{v_{BZ}}\frac{1}{\sqrt{Na}} e^{-iK_nx} \int e^{ikx} dk\\ &= \frac{1}{v_{BZ}}\frac{1}{\sqrt{Na}} e^{-iK_nx} \frac{1}{ix}\left[ e^{ikx} \right]_{\frac{-\pi}{a}}^{\frac{\pi}{a}} \\ &= \frac{1}{\sqrt{Na}} e^{-iK_nx} \frac{\sin(\pi x/a)}{\pi x/a} \end{align*}$$

最後の式で$1/v_{BZ} = 1/(2\pi/a)$を代入しました。最後の関数$\sin(\pi x/a)/(\pi x/a)$は原点付近に大きな値を持ち、そこから離れると急速に小さくなる関数

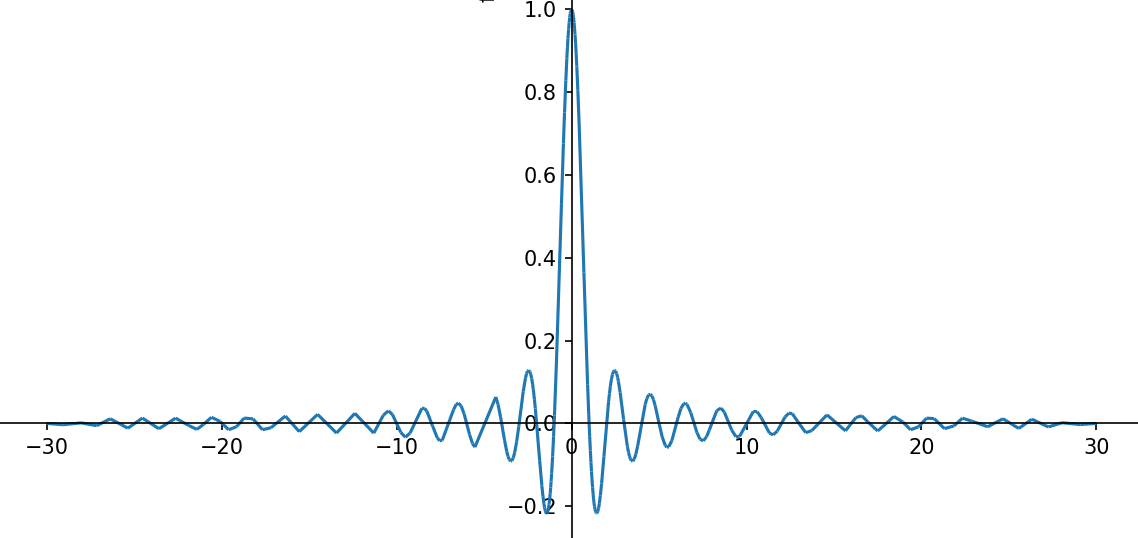
• 格子定数$a=1$として、$-30\leq Na \leq 30$まで$\frac{\sin(\pi x/a)}{\pi x/a}$をプロットしたグラフ

なので、これに格子間隔程度（またはそれより小さい）波長をもつ平面波$e^{iK_nx}$が掛け合わされた関数は、これは確信を持って「格子点の座標に局在した関数」ということができるでしょう。

なお上記の議論は平面波の場合だけでなく、一般に$u_{n,\boldsymbol{k}}(\boldsymbol{r})$がブロッホ波数依存性を持たない場合に苦労せず拡張できて、そのような場合具体的な関数形をもってWannier関数が格子座標に局在した関数であることを示すことができます。（ただ「$u_{n,\boldsymbol{k}}(\boldsymbol{r})$がブロッホ波数依存性を持たない」と言われても具体的にどういう場合に対応するのかがイメージしづらい気がしたので、より具体的な平面波（自由電子）の場合を例にとって説明しました）

おわりに

以上で本章の内容を終えます。最後に改めて本章で分かった内容をまとめておきます。

固体中の電子が従うべきBloch関数は、実空間上の格子点$\boldsymbol{R}$で指定されるWannier関数$w_{n,\boldsymbol{R}}(\boldsymbol{r})$を用いて、

$$\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) =\sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}},\\ w_{n,\boldsymbol{R}}(\boldsymbol{r}) = \frac{1}{N}\sum_{\boldsymbol{k}} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}$$

と展開でき、かつWannier関数は以下の性質を満たす：

並進性

$$w_{n,\boldsymbol{R}}(\boldsymbol{r}) =w_{n,0}(\boldsymbol{r}-\boldsymbol{R})\equiv w_{n}(\boldsymbol{r} - \boldsymbol{R})$$

正規直交性

$$\int_V w_{n'}^*(\boldsymbol{r}-\boldsymbol{R}')w_n(\boldsymbol{r} - \boldsymbol{R})dr = \delta_{n,n'}\delta_{\boldsymbol{R},\boldsymbol{R}'}$$

局在性（のイメージ）

脚注

1. このように広がった描像に対応するのが NFE(Nearly Free Electron)近似（ほとんど自由な電子近似） と呼ばれる、平面波（自由電子の固有関数）を近似の出発点とする考え方です。この近似の概要は「ほとんど自由な電子」というように周期ポテンシャルが小さい場合を考えて無摂動系として自由電子の波動関数を考え、小さい周期ポテンシャルを摂動として扱う考え方です。

2. Bloch関数に対する格子ベクトルの並進の関係を用いて$\int_V\varphi_{n',\boldsymbol{k}'}(\boldsymbol{r})^*\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})d\boldsymbol{r}=\sum_{\boldsymbol{R}}e^{i(\boldsymbol{k}-\boldsymbol{k}')\cdot\boldsymbol{R}}\int_{v_c}\varphi_{n',\boldsymbol{k}'}(\boldsymbol{r})^*\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})d\boldsymbol{r}=N\delta_{\boldsymbol{k},\boldsymbol{k}'}\int_{v_c}\varphi_{n',\boldsymbol{k}'}(\boldsymbol{r})^*\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})d\boldsymbol{r} =N\delta_{\boldsymbol{k},\boldsymbol{k}'}\sum_{\boldsymbol{K},\boldsymbol{K}'} c_{n',\boldsymbol{k}-\boldsymbol{K}'}^*c_{n,\boldsymbol{k}-\boldsymbol{K}}^*\int_{v_c}e^{i(\boldsymbol{K}-\boldsymbol{K}')\cdot\boldsymbol{r}} = N\delta_{\boldsymbol{k},\boldsymbol{k}'}\sum_{\boldsymbol{K}}c_{n',\boldsymbol{k}-\boldsymbol{K}}^*c_{n,\boldsymbol{k}-\boldsymbol{K}}$となるが、最後の式は$n,n'$で指定される固有値に対応する固有ベクトルの内積になっており、異なる固有値に対応する行列の固有ベクトルは直交する性質から最終的にブロッホ関数同士の内積が$N\delta_{\boldsymbol{k},\boldsymbol{k}'}\delta_{n,n'}$であることが示せる。

3. いくつかの教科書を読んだり頑張ってWEBで見つかる英語の文献を当たってみたりしてみましたのですが、Wannier関数は「局在している」とか「波束（Wave Pachket）だ」とかいう説明はあるのですがそれをどうやって示すのかが良くわかりませんでした

4. 上(I) 第10章脚注 18)

5. https://journals.aps.org/pr/abstract/10.1103/PhysRev.115.809