はじめに
前回記事で、tight-binding近似の基本となる原子核に強く束縛された多電子状態の波動関数について理解しました。これでようやく、固体の中の電子状態に入っていけます。
手始めに今回は数学的な準備として、固体、特に周期的な結晶が持つ周期性の取り扱いについて記載していきます。
すなわち、結晶中の物理量やハミルトニアンは、結晶と同じ周期性を持っており、周期性があるのであればFourier級数展開ができそうです。
とはいえ、結晶の周期は2次元・3次元のベクトルで表され、かつ様々な(直交とは限らない)方向を向いています。
そのような周期性・周期関数をどのように扱い、どのような展開をすれば良いのかについて今回は整理していきます。
私自身中々イメージが掴めず、(いつも通り?)回り道をしまくりながら冗長な内容となりましたが、その分他の解説よりはわかりやすい内容になっていると期待しています。
一方、冗長にやっている過程でミスや勘違いが多分に含まれている可能性もあるので、その点は注意していただければと思います。
それでは早速始めていきましょう。
結晶の周期性・Bravais格子ベクトル
本稿で最終的なゴールとしている固体は、ほとんどの場合原子や分子、イオンが周期的に配列した状態を想定しています。
それらの座標を格子点等と呼び、また座標に対応する位置ベクトルを (Bravais)格子ベクトルとよびます。
各格子ベクトルは一定の方向に周期性を持つので、最小単位となるベクトル\boldsymbol{a}_iを用いて
\boldsymbol{n} = n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3
のように書けます。このような各方向への周期性に対応するベクトル\boldsymbol{a}_iを基本並進ベクトルと呼び、また、全てのn_iの集合をBraveis格子と呼び、固体の周期性を表す指標になります。
まあ、そういう細かい名称はしっかりした教科書に譲ることにして、ぼちぼち進んで行きましょう。
代表的なBraveis格子
教科書などでよく出てくるBraveis格子は、以下のようなベクトルで表されます。
なお以下で\boldsymbol{e}_iはi = x,y,zとし、それぞれ直交座標のx,y,z軸に対する単位ベクトルを表します。
単純立方格子
\boldsymbol{a}_1 = a\boldsymbol{e}_x, \\
\boldsymbol{a}_2 = a\boldsymbol{e}_y,\\
\boldsymbol{a}_3 = a\boldsymbol{e}_z.
これは最も簡単な場合ですね。x軸、y軸、z軸に沿った周期性を持つような場合です。
面心立方格子
\boldsymbol{a}_1 = \frac{a}{2}\boldsymbol{e}_x + \frac{a}{2}\boldsymbol{e}_y, \\
{}\\
\boldsymbol{a}_2 = \frac{a}{2}\boldsymbol{e}_y + \frac{a}{2}\boldsymbol{e}_z,\\
{}\\
\boldsymbol{a}_3 = \frac{a}{2}\boldsymbol{e}_x + \frac{a}{2}\boldsymbol{e}_z.
体心立方格子
\boldsymbol{a}_1 = \frac{a}{2}\boldsymbol{e}_x + \frac{a}{2}\boldsymbol{e}_y
+ \frac{-a}{2}\boldsymbol{e}_z\\
{}\\
\boldsymbol{a}_2 = \frac{-a}{2}\boldsymbol{e}_x + \frac{a}{2}\boldsymbol{e}_y
+ \frac{a}{2}\boldsymbol{e}_z,\\
{}\\
\boldsymbol{a}_3 = \frac{a}{2}\boldsymbol{e}_x + \frac{-a}{2}\boldsymbol{e}_y
+ \frac{a}{2}\boldsymbol{e}_z.
面心立方格子や体心立方格子は、周期の最小単位が「斜め向き」になっており、直交座標に沿った周期をしていないことが分かるかと思います。
物理量の周期性
ここで、固体が上記のような周期性を持っていることから、固体中の物理量、例えば固体中の電子が感じるポテンシャルV(\boldsymbol{r})や電荷密度n(\boldsymbol{r})のような関数は、固体の周期性と同じく
V(\boldsymbol{r} + \boldsymbol{n}) = V(\boldsymbol{r})
のような周期関数となっているはずです。
そういう周期をどのように扱っていくのか、というのが本章のメインテーマです。
Fourier級数展開
1変数関数のFourier級数展開
周期関数と言えばFourier級数展開ですね。初めにもっとも簡単な例として
のような1次元の周期のみを考えると、これはよくある複素Fourier級数展開を用いて
f(x) = \sum_k C_k e^{ikx},\\
k = \frac{2\pi}{a}m, m = 0,\pm 1,\pm 2,\cdots,\\
C_k = \frac{1}{a}\int_0^a f(x)e^{-ikx}dx
と表せます
多変数関数のFourier 級数展開
上記のような展開を、多変数関数で、特に「斜め向き」の周期をもつような関数に対してどのように適用していけば良いのでしょうか。
単純立方格子の場合のFourier級数展開
初めに最も簡単な例として、斜め向きという点は一旦忘れて単純立方格子の基本併進ベクトルで表される周期をもつ関数V(\boldsymbol{r})を考えてみます。つまり格子ベクトルを
\begin{align*}
\boldsymbol{n} &= n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3\\
&=n_1a\boldsymbol{e}_x + n_2a\boldsymbol{e}_y + n_3a\boldsymbol{e}_z
\end{align*}
としたとき任意の\boldsymbol{n}について
V(\boldsymbol{r} + \boldsymbol{n}) = V(\boldsymbol{r})
となる関数のFourier展開を考えます。
\boldsymbol{r}を正規直交基底\boldsymbol{e}_iで成分表示すると、
V(x + n_1a,y,z) =V(x,y+n_2a,z) = V(x,y,z+n_3a) = V(x,y,z)
と、それぞれの座標成分に対して周期性を持ちます。そこで順次x座標から展開していきます。
以下でk_i= am_i/2\pi, m_i = 0,\pm 1,\pm 2\cdots (i = x,y,z)とます。
まずはy,zをある値に固定したと考えると、V(x,y,z)はxのみの1変数関数と考えることができます。
そこで先ほどと同じように
\begin{align*}
V(x,y,z) &= \sum_{k_x} C_{k_x}(y,z)e^{ik_xx}\\
C_{k_x}(y,z) &= \frac{1}{a}\int_0^aV(x,y,z)dx
\end{align*}
と展開できます。
ところでこの時の係数はC_{k_x}(y+n_2a,z) = C_{k_x}(y,z)と周期関数になっているわけで、
\begin{align*}
C_{k_x}(y,z) &=\sum_{k_y}C_{k_x,k_y}(z)e^{ik_yy},\\
C_{k_x,k_y}(z) &= \frac{1}{a}\int_0^a C_{k_x}(y,z)e^{-ik_yy}dy\\
&= \frac{1}{a^2}\int_0^a \int_0^a V(x,y,z)e^{-i(k_xx + k_yy)}dxdy
\end{align*}
と展開できます。さらにzについても
\begin{align*}
C_{k_x,k_y}(z) &=\sum_{k_z}C_{k_x,k_y,k_z}e^{ik_zz},\\
C_{k_x,k_y,k_z} &= \frac{1}{a}\int_0^a C_{k_x,k_y}(z)e^{-ik_zz}dz\\
&= \frac{1}{a^3}\int_0^a\int_0^a\int_0^a V(x,y,z)e^{-i(k_xx + k_yy + k_zz)}dxdydz
\end{align*}
と、順次各座標について展開していけば、全部合わせて
V(x,y,z) = \sum_{k_x,k_y,k_z}C_{k_x,k_y,k_z}e^{i(k_xx + k_yy + k_zz)}\\
C_{k_x,k_y,k_z}= \frac{1}{a^3}\int_0^a\int_0^a\int_0^a V(x,y,z)e^{-i(k_xx + k_yy + k_zz)}dxdydz
となります。
ただしこのままだと位置ベクトル\boldsymbol{r}に対して、基底を選んで成分表示する必要がある形になっています。そこで
\boldsymbol{k} = k_x\boldsymbol{e}_x + k_y\boldsymbol{e}_y + k_z\boldsymbol{e}_z
というベクトルを定義すると、
\begin{align*}
\boldsymbol{k}\cdot\boldsymbol{r} &= k_x\boldsymbol{e}_x\cdot\boldsymbol{r} +
k_y\boldsymbol{e}_y\cdot\boldsymbol{r} +
k_z\boldsymbol{e}_z\cdot\boldsymbol{r} \\
&= k_xx + k_yy + k_zz
\end{align*}
と基底を気にせずにベクトルの内積の形で書くことができます。以上より単純立方格子の周期をもつ関数のFourier展開は
V(\boldsymbol{r}) = \sum_{\boldsymbol{k}}C_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot\boldsymbol{r}}\\
C_{\boldsymbol{k}}= \frac{1}{v_c}\int_{v_c} V(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}d\boldsymbol{r}
と、シンプルな形で書けました。ただし、\sum_{\boldsymbol{k}}はk_x,k_y,k_zそれぞれの総和、v_cは繰り返しの最小単位の体積を表し、v_c = a^3, \int_{v_c}d\boldsymbol{r}=\int_0^adx\int_0^ady\int_0^adzです。
非直交な周期性を持つ関数のFourier展開(2次元)
ここまでは特に引っかかることもなく進めましたが、満を持して「斜め向き」の周期を考えていきます。
例えば先ほど例に示したように、面心立方格子や体心立方格子のような周期性を扱うには、直交しない方向への周期性を考える必要があります。
まずは関数のイメージがしやすい、2次元の場合を考えてみましょう。
関数V(\boldsymbol{r})が図のような、
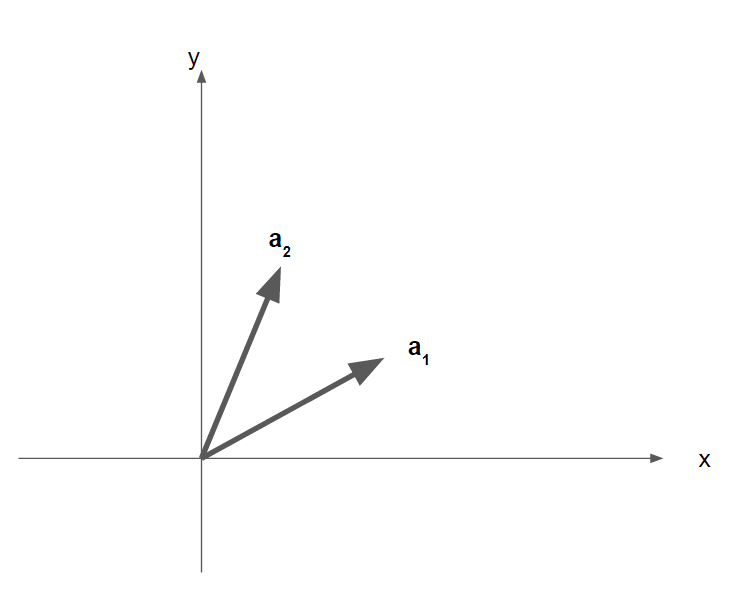
基本併進ベクトル\boldsymbol{a}_1 , \boldsymbol{a}_2に対して周期性を持つ場合のFourier展開について考えてみます。
ここで|\boldsymbol{a}_1| =a_1, |\boldsymbol{a}_2|=a_2として関数の周期と平行な単位ベクトル
\boldsymbol{e}_1 = \frac{\boldsymbol{a}_1}{a_1}, \boldsymbol{e}_2 = \frac{\boldsymbol{a}_2}{a_2}
を基底として成分表示をすることにします。
\begin{align*}
\boldsymbol{r} &= r_1\boldsymbol{e}_1 + r_2\boldsymbol{e}_2\\
&= (r_1,r_2)
\end{align*}
このような斜交基底を定義しても任意の位置\boldsymbol{r}を表すことができますが、下図のようにr_iは、直交基底の場合と異なり\boldsymbol{e}_1\cdot\boldsymbol{r}ではないことに注意してください。(じゃあどうすればいいのかというと、後でわかります)
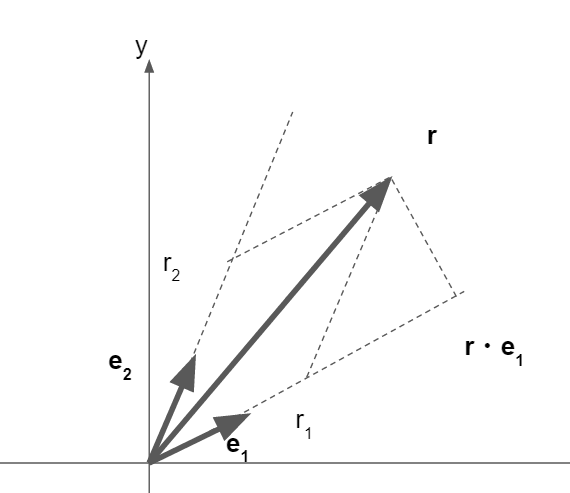
このように成分表示すると、関数の周期性は
V(r_1+n_1a_1,r_2) = V(r_1,r_2 + n_2a_2) = V(r_1,r_2)
と書けます。このように書けば先ほどの直交基底で座標を表した場合と同じように扱えます。そこで先ほどと同じように、例えばまずr_2を固定してr_1についてFourier展開し、その係数をさらにr_2について展開する、というように各成分に対して順次Fourier展開をすると、
V(r_1,r_2) = \sum_{k_1,k_2}C_{k_1,k_2}e^{i(k_1r_1 + k_2r_2)}\\
C_{k_1,k_2}= \frac{1}{a_1a_2}\int_0^{a_1}\int_0^{a_2} V(r_1,r_2)e^{-i(k_1r_1 + k_2r_2)}dr_1dr_2,\\
k_i = \frac{2\pi}{a_i}m_i, m_i = 0,\pm 1,\pm 2,\cdots
と書けます。ところで今回も基底ベクトルに依存した成分表示になっており、特に斜交座標の成分表示なので使いにくい形になっています。
そこで先ほどと同じように、基底座標を意識しなくても自動的に上記のような形になるようなベクトル\boldsymbol{k}を定義したいのですが、どうすれば良いでしょうか。
素朴に
\widetilde{\boldsymbol{k}}= k_1\boldsymbol{e}_1+k_2\boldsymbol{e}_2
としてみても、今回は先述のように\boldsymbol{e}_1\cdot\boldsymbol{r}=r_1とできず、
\widetilde{\boldsymbol{k}}\cdot\boldsymbol{r} \neq k_1r_1 + k_2r_2
となってしまいます。そこで上手いこと、
\boldsymbol{e}_i^* \cdot\boldsymbol{r} = r_i
となってくれるようなベクトル\boldsymbol{e}_i^*を見つければ、これを用いて
\boldsymbol{k} = k_1\boldsymbol{e}_1^* + k_2\boldsymbol{e}_2^*
と置けば、
\boldsymbol{k} \cdot \boldsymbol{r}
=
k_1\boldsymbol{e}_1^*\cdot\boldsymbol{r}
+
k_2\boldsymbol{e}_2^*\cdot\boldsymbol{r}
=
k_1r_1 + k_2r_2
と直交座標の場合と同じ形に書けそうです。
そこで、\boldsymbol{e}_i^* \cdot\boldsymbol{r} = r_iを満たす\boldsymbol{e}_i^*を考えるために改めて\boldsymbol{r}を\boldsymbol{e}_1,\boldsymbol{e}_2で展開してみると、
\boldsymbol{r} = r_1\boldsymbol{e}_1 + r_2\boldsymbol{e}_2
なので、\boldsymbol{e}_1との内積が1で、\boldsymbol{e}_2に直交するようなベクトル\boldsymbol{e}^*_1と、逆に
\boldsymbol{e}_2との内積が1で、\boldsymbol{e}_1に直交するベクトル\boldsymbol{e}^*_2を考えればよさそうです。
まず\boldsymbol{e}_2と直交するという条件を考えてみると、「2つのベクトルと直交する方向を持つベクトル」として定義される外積が使えそうです。
今回は\boldsymbol{e}_2と直交してさえいればいいので、もう一つのベクトルの向きはある程度任意性がありそうですが、\boldsymbol{r}と同じ平面上にある方が良さそうなので\boldsymbol{e}_1, \boldsymbol{e}_2と直交し大きさが1のベクトル(つまりz方向の単位ベクトル)\boldsymbol{n}を導入し、Aを後で調整する定数として
\boldsymbol{e}_1^* = A\boldsymbol{e}_2\times\boldsymbol{n}
\boldsymbol{e}_2^*についても同様に
\boldsymbol{e}_2^* = B\boldsymbol{n}\times\boldsymbol{e}_1
と置けば良さそうです。(3次元の場合と整合性を取るために外積の順番は逆にしておきます)
続いて\boldsymbol{e}_1^*\cdot\boldsymbol{e}_1=\boldsymbol{e}_2^*\cdot\boldsymbol{e}_2=1の条件を考えると、
\boldsymbol{e}_1^*\cdot\boldsymbol{e}_1
=
A(\boldsymbol{e}_2\times\boldsymbol{n})
\cdot \boldsymbol{e}_1 = 1\\
\boldsymbol{e}_2^*\cdot\boldsymbol{e}_2
=
B(\boldsymbol{n}\times\boldsymbol{e}_1)
\cdot \boldsymbol{e}_2 = 1
を満たせばよいので、(\boldsymbol{e}_i\times\boldsymbol{n})\cdot \boldsymbol{e}_jはスカラーなのでその逆数を選べば良くて、最終的に
\boldsymbol{e}_1^* = \frac{\boldsymbol{e}_2\times\boldsymbol{n}}{\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{n})},
\boldsymbol{e}_2^* = \frac{\boldsymbol{n}\times\boldsymbol{e}_1}{\boldsymbol{e}_2\cdot(\boldsymbol{n}\times\boldsymbol{e}_1)},
と定義すれば、任意のベクトル\boldsymbol{r}に対して
\boldsymbol{e}_1^*\cdot\boldsymbol{r}=r_1,\\
\boldsymbol{e}_2^*\cdot\boldsymbol{r}=r_2
が満たされることになります。
したがって、
\begin{align*}
\boldsymbol{k} =
k_1\boldsymbol{e}_1^*
+
k_2\boldsymbol{e}_2^*
=
k_1\frac{\boldsymbol{e}_2\times\boldsymbol{n}}{\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{n})}
+
k_2 \frac{\boldsymbol{n}\times\boldsymbol{e}_1}{\boldsymbol{e}_2\cdot(\boldsymbol{n}\times\boldsymbol{e}_1)}
\end{align*}
と定義すれば、
\boldsymbol{k}\cdot\boldsymbol{r} = k_1r_1 + k_2r_2
を満たし、関数e^{i\boldsymbol{k}\cdot\boldsymbol{r}}を用いて関数を展開することができました。
なお、この
e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
は、\boldsymbol{k}方向に進む平面波を表すため、これまで見たような多変数関数のFourier級数展開を平面波展開と呼ぶこともあります。
以上をまとめると、周期\boldsymbol{a}_1,\boldsymbol{a}_2を持つ2次元関数
V(\boldsymbol{r} + \boldsymbol{a}_1)
= V(\boldsymbol{r} + \boldsymbol{a}_2)
= V(\boldsymbol{r})
に対して、Fourier展開を
\begin{align*}
V(\boldsymbol{r}) &= \sum_{k_1,k_2}C_{k_1,k_2}e^{i(k_1r_1 + k_2r_2 )}
=
\sum_{\boldsymbol{k}}C_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot\boldsymbol{r}}\\
C_{k_1,k_2}&= \frac{1}{a_1a_2}\int_0^{a_1}\int_0^{a_2} V(r_1,r_2)e^{-i(k_1r_1 + k_2r_2 )}dr_1dr_2\\
&=
\frac{1}{s_c}\int_{s_c} V(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}d\boldsymbol{r}
\end{align*}
と平面波の和の形に書けることがわかりました。
なお、ここでは斜交座標なので\boldsymbol{a}_1と\boldsymbol{a}_2のなす角を\thetaとして、繰り返しの最小単位の面積をs_c = a_1a_2\sin\thetaとし、
積分
\int_{s_c}d\boldsymbol{r}=\int_0^{a_1}\int_0^{a_2}\sin\theta dr_1dr_2です。
もう少し図式的なイメージで理解する
ところで、先ほどは\boldsymbol{k}\cdot \boldsymbol{r} = k_1r_1 + k_2r_2となる\boldsymbol{k}を発見的に考えたわけですが、これはグラフで考えてみるとよくイメージできます。
実はこのあたりの理解で極めて混乱してしまい、長らく三角関数の沼にはまっておりました。分かってしまえばシンプルなものでした。分かっている人からすれば当たり前の内容なのかもしれませんが、中には私のように混迷を極める人もいるかと思いますので、折角なので丁寧にまとめていこうと思います。
斜交座標での平面波
もともと、斜交座標r_1, r_2のもとで関数
e^{i(k_1r_1 + k_2r_2)} = \cos(k_1r_1+k_2r_2) + i\sin(k_1r_1 + k_2r_2)
を考えているわけですが、簡単のために\cosだけを考え、
k_1 = 2\pi/a,k_2 = 0の場合を考えると、
\cos(\frac{2\pi}{a_1}r_1)
はr_1が同じ値を取る範囲で、一定の値を持ち、かつ変数r_1について周期a_1をもつ2次元関数です。特に\cos(\frac{2\pi}{a_1}r_1) = 1となる領域を3つ図示してみると、
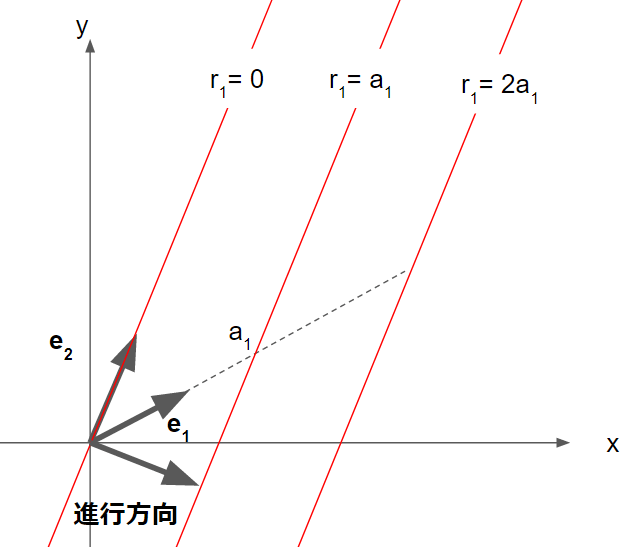
こんな直線になります。関数の値をz軸方向に取って3次元でプロットしてみるとこんな感じです
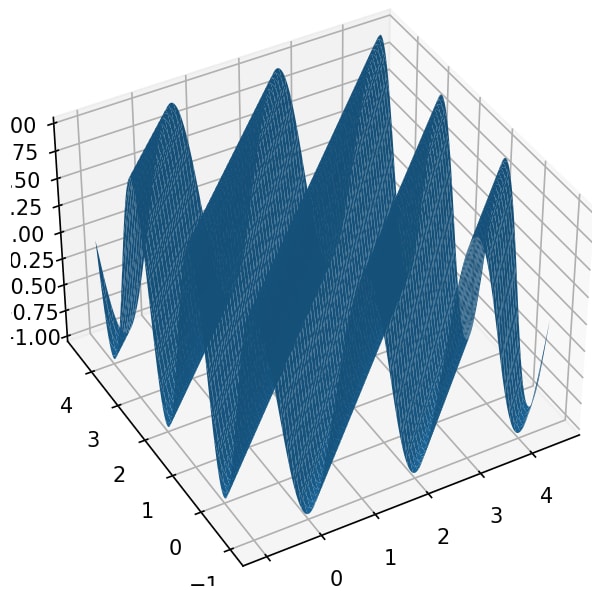
これは見るからに、\boldsymbol{e}_2と直交した向きへ進む平面波ですが、実際同位相面(今は2次元なので同位相「直線」)がベクトル\boldsymbol{e}_2と平行なので、その進行方向は\boldsymbol{e}_2と直交した向きを持つわけでした。
また、図から、\boldsymbol{e}_1, \boldsymbol{e}_2のなす角を\thetaとすれば、進行方向についての周期はa_1\sin\thetaとなります。
今考えているk_1 = 2\pi/a_1,k_2 = 0の場合に対応する波数ベクトルを\boldsymbol{k}_{10}とすると、
|\boldsymbol{k}_{10}| = \frac{2\pi}{a\sin\theta}
ですが、これはまさに先ほど定義したベクトルの大きさ
\left|
\frac{\boldsymbol{e}_2\times\boldsymbol{n}}{\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{n})}
\right| = \frac{1}{\cos(\frac{\pi}{2}-\theta)} = \frac{1}{\sin\theta}
と対応してるわけでした。これはk_1として2\pi/a_1の整数倍を選んでもa_1\rightarrow a_1/mとすれば同様に考えられます。
というわけで先ほどのように「内積を取った値がk_1r_1になれば良いのだから・・・」等と考えるまでもなく、e^{ik_1r_1}はmを整数として
\boldsymbol{k}_{1} \equiv
k_1\boldsymbol{e}_1^*,\\
\boldsymbol{e}_1^* = \frac{\boldsymbol{e}_2\times\boldsymbol{n}}{\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{n})},\\
k_1 = \frac{2\pi}{a_1}m
と置けば(\boldsymbol{k}_1がベクトルであることに注意してください)、
e^{ik_1r_1} = e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}
であることがイメージできたかと思います。
k_1 = 0, k_2 = \frac{a_2m_2}{2\pi}の場合も同様に、任意のmに対して
e^{ik_2r_2} = e^{i\boldsymbol{k}_2\cdot\boldsymbol{r}}
となります。
最後にk_1\neq 0,k_2\neq 0の場合は、
e^{i(k_1r_1+k_2r_2)} = e^{ik_1r_1}e^{ik_2r_2} = e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}e^{i\boldsymbol{k}_2\cdot\boldsymbol{r}}
=
e^{i(\boldsymbol{k}_1\cdot\boldsymbol{r} + \boldsymbol{k}_2\cdot\boldsymbol{r})}
なので
\boldsymbol{k} = \boldsymbol{k}_1 + \boldsymbol{k}_2 = k_1\boldsymbol{e}_1^*
+
k_2\boldsymbol{e}_2^*
として、
e^{i(k_1r_1 + k_2r_2)} = e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
になります。
結局、私は平面波の進行方向が、\boldsymbol{e}_1, \boldsymbol{e}_2と「垂直」という点に引っ張られすぎていて、ずっと違和感を覚えていたように思います。どちらかというと、\boldsymbol{e}_1, \boldsymbol{e}_2と「平行」に同位相面(直線)が並んでいると考えればスッキリとイメージできたのでした。
具体的に、x軸と平行方向に周期1、斜め45°方向に周期\sqrt{2}の場合、つまり\boldsymbol{a}_1 = (1,0), \boldsymbol{a}_2 =(1,1)の場合、k_1 = 2\pi/a_1, k_2 = 2\pi/a_2として
\sin(k_1r_1) \sin(k_2r_2)
の等高線をプロットしてみます。すると下図のように、繰り返しの最小単位(Unit Cell)に沿った周期関数の総和を考えているのだとイメージできます。
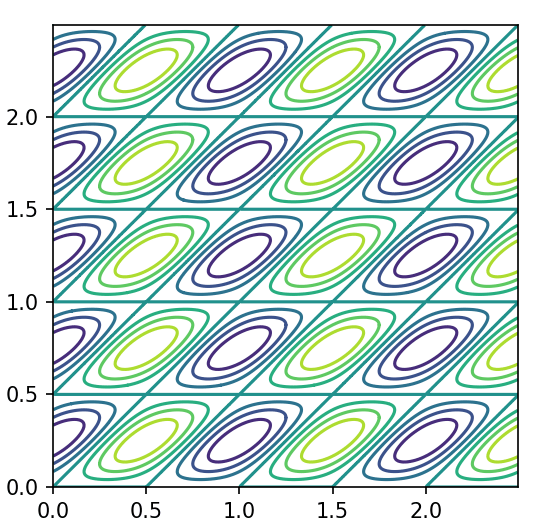
k_2を2倍にしてみましょう。すると\boldsymbol{a}_2方向の波数(=振動数)が2倍になります。
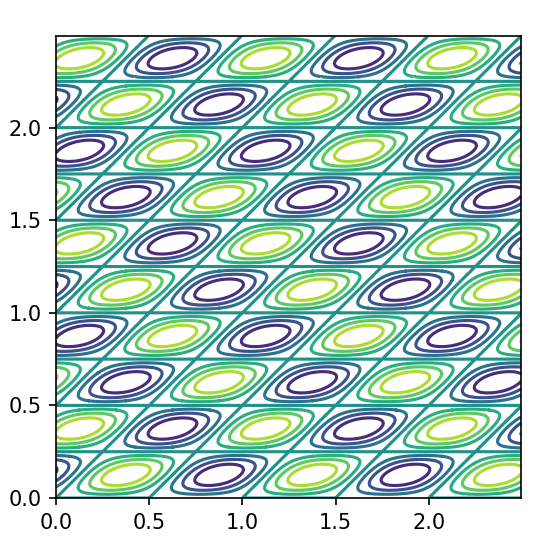
k_2をどんどん細かくして行き、それらの\sin, \cosをすべて足し合わせると、r_2方向に対しては連続的な係数を持ち、r_1方向に対してはそれぞれr_2を固定して1変数関数とみなした場合のFourier展開の形になるわけでした。
これで(私は)ようやく、非直交な周期をもつ周期関数のFourier展開についてイメージを持てました。
非直交な周期性を持つ関数のFourier展開(3次元)
2次元の場合と同様に、3次元の非直交な周期
\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3
を持つ関数
V(\boldsymbol{r}+\boldsymbol{a}_1)
=
V(\boldsymbol{r}+\boldsymbol{a}_2)
=
V(\boldsymbol{r}+\boldsymbol{a}_3)
=
V(\boldsymbol{r})
も、\boldsymbol{a}_i方向の単位ベクトルを\boldsymbol{e}_iとして、それらを基底に
\boldsymbol{r} = \sum_ir_i\boldsymbol{e}_i
と置くと、
「\boldsymbol{e}_2と\boldsymbol{e}_3に直交して\boldsymbol{e}_1との内積が1のベクトル」\boldsymbol{e}_1^*、
「\boldsymbol{e}_1と\boldsymbol{e}_3に直交して\boldsymbol{e}_2との内積が1のベクトル」\boldsymbol{e}_2^*、
「\boldsymbol{e}_1と\boldsymbol{e}_2に直交して\boldsymbol{e}_3との内積が1のベクトル」\boldsymbol{e}_3^*
を用いて、
\boldsymbol{k} = k_1\boldsymbol{e}_1^*
+
k_2\boldsymbol{e}_2^*
+
k_3\boldsymbol{e}_3^*
として、Fourier展開
V(\boldsymbol{r}) = \sum_{\boldsymbol{k}}C_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot\boldsymbol{r}}\\
C_{\boldsymbol{k}}= \frac{1}{v_c}\int_{v_c} V(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}d\boldsymbol{r}
と表すことができます。ただし、\boldsymbol{e}_i^*はそれぞれ、
\boldsymbol{e}_1^*
=
\frac{\boldsymbol{e}_2\times\boldsymbol{e}_3}{\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{e}_3)}
\boldsymbol{e}_2^*
=
\frac{\boldsymbol{e}_3\times\boldsymbol{e}_1}{\boldsymbol{e}_2\cdot(\boldsymbol{e}_3\times\boldsymbol{e}_1)}
\boldsymbol{e}_3^*
=
\frac{\boldsymbol{e}_1\times\boldsymbol{e}_2}{\boldsymbol{e}_3\cdot(\boldsymbol{e}_1\times\boldsymbol{e}_2)}
で、v_cは\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3で囲まれる平行六面体の体積\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)で、1/v_c\int_{v_c}d\boldsymbol{r} = 1/(a_1a_2a_3)\int_0^{a_1}dr_1\int_0^{a_2}dr_2\int_0^{a_3}dr_3です。
なお、(単純)立方格子のように直交した周期性を持つ場合は、
\boldsymbol{e}_y\times\boldsymbol{e}_z = \boldsymbol{e}_x, \boldsymbol{e}_z\times\boldsymbol{e}_x = \boldsymbol{e}_y,\boldsymbol{e}_x\times\boldsymbol{e}_y = \boldsymbol{e}_z
となることから\boldsymbol{e}_i^* = \boldsymbol{e}_iとなります。
逆格子ベクトル
以上で、任意の周期を持つ関数に対してFourier展開を定義することができました。
ここで、
k_i = \frac{2\pi}{a_i}m_i, m_i = 0,\pm 1,\pm 2,\cdots
と
\frac{\boldsymbol{e}_j\times\boldsymbol{e}_l}{a_i\boldsymbol{e}_i\cdot(\boldsymbol{e}_j\times\boldsymbol{e}_l)}
=
\frac{\boldsymbol{a}_j\times\boldsymbol{a}_l}{\boldsymbol{a}_i\cdot(\boldsymbol{a}_j\times\boldsymbol{a}_l)}
から、\boldsymbol{k}を
\begin{align*}
\boldsymbol{k}
&= k_1\frac{\boldsymbol{e}_2\times\boldsymbol{e}_3}{\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{e}_3)}
+
k_2\frac{\boldsymbol{e}_3\times\boldsymbol{e}_1}{\boldsymbol{e}_2\cdot(\boldsymbol{e}_3\times\boldsymbol{e}_1)}
+
k_3\frac{\boldsymbol{e}_1\times\boldsymbol{e}_2}{\boldsymbol{e}_3\cdot(\boldsymbol{e}_1\times\boldsymbol{e}_2)}\\
&=
m_1\frac{2\pi\boldsymbol{e}_2\times\boldsymbol{e}_3}{a_1\boldsymbol{e}_1\cdot(\boldsymbol{e}_2\times\boldsymbol{e}_3)}
+
m_2\frac{2\pi\boldsymbol{e}_3\times\boldsymbol{e}_1}{a_2\boldsymbol{e}_2\cdot(\boldsymbol{e}_3\times\boldsymbol{e}_1)}
+
m_3\frac{2\pi\boldsymbol{e}_1\times\boldsymbol{e}_2}{a_3\boldsymbol{e}_3\cdot(\boldsymbol{e}_1\times\boldsymbol{e}_2)}\\
&=
m_1\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
m_2\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
m_3\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}\\
&\equiv
m_1\boldsymbol{b}_1 + m_2\boldsymbol{b}_2 + m_3\boldsymbol{b}_3
\end{align*}
とも書けます。これならいちいち「\boldsymbol{a}_i方向の単位ベクトル」等と考える必要もなく、与えられた周期に対応するベクトル\boldsymbol{a}_iを使って直接波数ベクトル\boldsymbol{k}を定義できます。
物性物理(固体物理)の分野では、結晶の周期を表すベクトル
\boldsymbol{n} = n_1\boldsymbol{a}_1
+
n_2\boldsymbol{a}_2
+
n_3\boldsymbol{a}_3
を格子ベクトルと呼ぶことに対応して、このようなベクトル
\boldsymbol{k} = m_1\boldsymbol{b}_1 + m_2\boldsymbol{b}_2 + m_3\boldsymbol{b}_3
を逆格子ベクトルと呼び、m_iを指定して得られる各\boldsymbol{k}が示す座標を逆格子点と呼びます。
また、逆格子ベクトルであることを強調する意味(多分)で小文字の\boldsymbol{k}ではなく、大文字の\boldsymbol{K}や\boldsymbol{G}と表すことが多いです。
この時、任意の格子ベクトル\boldsymbol{n}に対して、
\boldsymbol{b}_i\cdot\boldsymbol{a}_j = 2\pi\delta_{ij}
となることから、
\boldsymbol{K}\cdot\boldsymbol{r} = 2\pi l, l = 0,1,2,\cdots
となります。
なお、逆格子ベクトル・逆格子点は単に計算上出てくるだけのものではなく、実験などで直接観測される値として物理的な意味を持っています。こちらについては章を改めて、次章でまとめていこうと思います。
まとめ
今回は普通の教科書ではさらっと出てくる逆格子ベクトルについて、(必要以上に?)詳しく考えてみました。
改めてまとめると、結晶が持つ周期は、周期の最小単位を\boldsymbol{a}_iとして、それらの様々な和
\begin{align*}
\boldsymbol{n} &= n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3\\
\end{align*}
とする格子ベクトルによって表され、結晶と同じ周期性を持つ関数
V(\boldsymbol{r} + \boldsymbol{n}) = V(\boldsymbol{r})
のFourier級数展開は、逆格子ベクトル\boldsymbol{k}を
\begin{align*}
\boldsymbol{k}
&=
m_1\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
m_2\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
m_3\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}\\
&\equiv
m_1\boldsymbol{b}_1 + m_2\boldsymbol{b}_2 + m_3\boldsymbol{b}_3
\end{align*}
と定義することで、Fourier級数展開は以下のように書くことができます。
V(\boldsymbol{r}) = \sum_{\boldsymbol{k}}C_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot\boldsymbol{r}}\\
C_{\boldsymbol{k}}= \frac{1}{v_c}\int_{v_c} V(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}d\boldsymbol{r}
上記のような逆格子ベクトルは物理的な意味を持ち、それについては次章でまとめる予定です。
初めはこの章で終えるつもりで書き出したのですが、書きながら考えているうちにどんどん量が増えてしまいました。
何か質問や、ご指摘、感想などあればお気軽にコメントいただければ幸いです。(特に途中大いに勘違いや間違いをしている可能性もあるので)
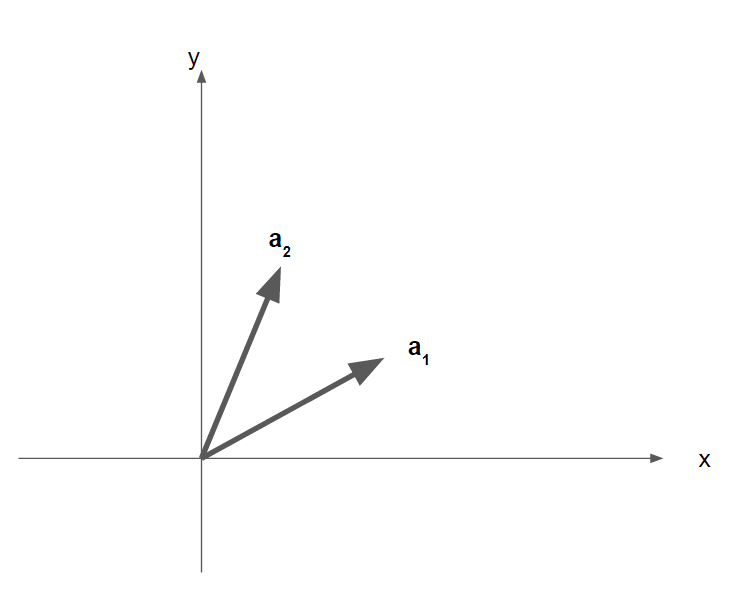





Discussion